基于桥梁动力响应的应变影响线提取
王宁波1,任伟新2,何立翔1
(1. 中南大学 土木工程学院,湖南 长沙,410075;
2. 合肥工业大学 土木与水利工程学院,安徽 合肥,230009)
摘要:对已知标定车辆过桥产生的桥梁动应变响应进行反演计算得到相应测点的应变影响线,实现桥梁影响线动态测试。分析不同支撑边界条件下桥梁影响线的描述机理,在此基础上对动态测试的初始影响线结果进行多项式分段拟合以去除桥梁振动干扰影响,提取具有准静态特性的影响线,从数值模拟和现场试验进行验证研究。研究结果表明:所提出的拟合方法对不同类型边界条件桥梁都可从动力响应中准确提取应变影响线;各种行车工况下影响线提取结果基本一致,证实多项式分段拟合方法在去除桥梁振动干扰的同时还能较好地保证提取结果的正 确性。
关键词:应变;影响线;多项式拟合;标定车辆;动态测试
中图分类号:U441 文献标志码:A 文章编号:1672-7207(2014)12-4362-08
Extraction of strain influence line of bridge from dynamic responses
WANG Ningbo1, REN Weixin2, HE Lixiang1
(1. School of Civil Engineering, Central South University, Changsha 410075, China;
2. School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)
Abstract: The strain influence line of measure points on bridge structure was obtained by inversing the dynamic response of calibrated vehicle crossing the bridge structure. Based on the theory mechanism analysis of the bridge strain influence line of different boundary conditions, the idea of using a polynomial segment function to fit the initial result was explored to remove the interference caused by bridge vibration and extract the quasi-static influence line. The results of the numerical simulation and the field test indicate that the proposed piecewise polynomial fitting method can extract the bridge strain influence line under different boundary conditions. Furthermore, all extracted influence lines by fitting method are basically the same as each other despite the change of initial results with driving condition, which verifies that the piecewise polynomial fitting method has good capability of removing the influence resulting from bridge vibration and ensures the accuracy of the results.
Key words: strain; influence line; polynomial fitting; calibrated vehicle; dynamic testing
桥梁应变影响线描述桥梁在移动单位荷载作用下的静态特性,综合反映桥梁的边界条件、几何信息和物理信息,是桥梁结构重要的特征参数之一。结合桥梁影响线用于模型修正[1]、损伤识别[2]、桥梁结构评定等问题的研究[3-4],能克服结构模态测试数据不完备问题,同时具备直观、经济、实用的特点。通过比较不同时期桥梁影响线来评定结构发展变化是一种桥梁结构承载能力评定的新思路。不仅如此,对于桥梁动态称重(bridge-WIM)问题,桥梁应变影响线则能提供重要的结构参数信息,直接关系着Bridge-WIM测试精度[5-8]。桥梁应变影响线理论上可由桥梁的设计参数计算得到。在实际情况中,由于边界条件不确定(介于理想简支和固支之间,且存在变异)、材料老化、弹性铺装等因素使得计算结果不理想,往往与实际值存在较大偏差,目前一般通过实测手段来获取桥梁应变影响线。方法之一是采用递推法作为静载试验的方式逐点测试桥梁应变影响线[9]。这种静态测试的影响线实际上为一系列离散点,数据信息量有限,在应用方面具有局限性。从动态测试角度获取桥梁应变影响线是目前比较广泛的做法,其基本思路是通过对已知标定车辆匀速过桥产生的动应变响应进行反演计算得到实际桥梁应变影响线。O'Brien等[10-12]采用不同车辆对不同类型桥梁进行标定测试和影响线提取研究。一般地,根据动应变反演计算的影响线不可避免地包含桥梁振动信息,尤其对于简支边界条件振动干扰更加明显,且随车辆行驶速度增加而增大。这种简单分离后的结果可认为是单位荷载作用下的“动力响应”,不足以体现影响线的准静态特性[13]。对反演计算的应变影响线进行滤波处理虽能在一定程度上消除桥梁振动的影响,但该方法势必会导致影响线幅值及精度降低[14]。准确提取能够反映准静态特性且数据信息量丰富的桥梁应变影响线将有利于更好地发挥其应用价值,这方面的研究尚不多见。为此,本文作者以影响线动态标定测试为基础,结合动力响应和车辆参数反演计算初始应变影响线。通过研究影响线理论机理,对初始结果进行多项式分段拟合提取具有准静态特性的桥梁应变影响线,去除桥梁振动干扰,提升影响线测试精度。从数值分析和现场试验的角度研究车辆过桥时桥梁不同测点应变影响线提取问题,以验证本文多项式分段拟合方法的优势。
1 桥梁应变影响线动态测试方法
通过动态测试获取实际桥梁的应变影响线是目前的一种有效方式。该方法不需知道桥梁的支撑边界、材料等信息,尤其适合于桥梁年限久、结构参数缺失或未知的情况。桥梁应变影响线动态测试的具体方法及影响线的提取如下:选定具有代表性的车辆作为测试车辆,在静止状态下测定车辆轴距Di(Di表示第i轴与第1轴的距离,其中D1=0)、各轴重Ai及桥长Lb。控制该标定车辆以恒定速度v行驶通过待测试桥梁。v取值不宜过大,以避免激起桥梁大幅振动而造成实测应变影响线存在较大波动,以采样频率f记录桥上测点动应变时程曲线。根据动力响应反演计算提取各测点应变影响线向量I,具体计算过程如下:
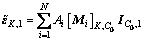 (1)
(1)
其中:

Ci=Dif/v (3)
C0=Lbf/v (4)
K=C0+CN (5)
定义误差函数如下:
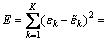
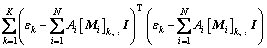 (6)
(6)
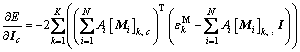 (7)
(7)
求影响线向量I时,根据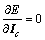 计算化简得(其中,c=1,2,…,C0):
计算化简得(其中,c=1,2,…,C0):
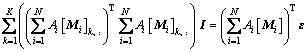 (8)
(8)
令 ,
,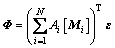 ,则
,则
 (9)
(9)
式中:ε为动应变实际测试值;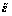 为影响线拟合的动应变理论值;Mi为与第i车轴对应的转换矩阵,[Mi]k,:为[Mi]的第k行向量;I为测点影响线;N为车辆车轴总数;i为车轴数,i=1,…,N;c为影响线向量测点数;K为采样点总数;k表示第k个采样点;C0为与桥长Lb相对应的采样点数。经计算化简可得出W是行和列均为C0的方阵。式(8)中,除影响线向量I外,其他参数均为已知,以此计算
为影响线拟合的动应变理论值;Mi为与第i车轴对应的转换矩阵,[Mi]k,:为[Mi]的第k行向量;I为测点影响线;N为车辆车轴总数;i为车轴数,i=1,…,N;c为影响线向量测点数;K为采样点总数;k表示第k个采样点;C0为与桥长Lb相对应的采样点数。经计算化简可得出W是行和列均为C0的方阵。式(8)中,除影响线向量I外,其他参数均为已知,以此计算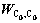 和
和 ,对式(9)矩阵求逆可计算得到应变影响线。
,对式(9)矩阵求逆可计算得到应变影响线。
在实际测试时,一般采用不同车辆、不同行驶速度等多种工况下测定的应变影响线取平均。对于正交异性板桥、整体式板桥等还需考虑车辆横向位置对测点影响线的影响,标定测试时应采用车辆行驶在不同横向位置的工况,测试提取不同横向作用位置对应的应变影响线。
反演计算方法虽然能够实现从动力响应中提取影响线,但影响线“测试”结果受桥梁振动干扰,对于同一测点,不同工况下因振动干扰程度不同而导致测试的应变影响线结果不同,需探索有效方法以准确提取具有准静态特性的影响线。
2 多项式分段拟合
根据标定已知车辆过桥产生的桥梁动力响应反演计算得到的应变影响线,其实质是桥梁在单位移动荷载作用下的动力响应,不可避免地包含桥梁振动信息受行车速度、路面不平度等因素影响。根据影响线理论机理,采用多项式分段拟合的思路可从包含桥梁振动信号的初始结果中拟合具有准静态特性的应变影响线,在提取有用信息的同时,去除干扰项的影响,更能保证测试结果的准确性。一般地,不同类型支撑边界条件下的应变影响线如下。
2.1 简支边界
理想简支边界条件下,离端部距离a处截面测点应变影响线方程为
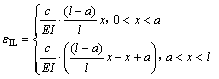 (10)
(10)
2.2 固支边界
在理想固支边界条件下,离端部距离a处截面测点应变影响线方程为
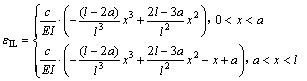 (11)
(11)
2.3 介于简支和固支之间
对于此类情况,假定两端扭转约束刚度分别为k1和k2,如图1所示。
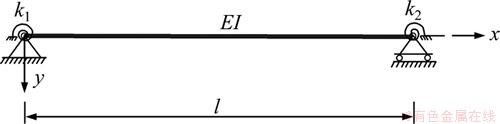
图1 两端具有转动弹性约束的简支梁
Fig. 1 Simply supported beam with rotating elastic constraints on both ends
此时,两端弯矩分别为:
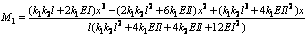
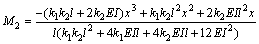
离端部距离a处截面测点应变影响线用M1和M2表示如下:
 (12)
(12)
式中:EI为梁的抗弯刚度;E为弹性模量;I为截面惯性矩;l为梁长度;c为梁上测点与中性轴的距离。
从上述理论分析可以看出:对于理想简支梁桥,桥梁任意截面测点的应变影响线εIL(纵向)用直线分段描述;对于带有转动弹性约束桥梁和固支梁桥,其相应的应变影响线可用三次曲线分段描述。结合这类特性,对实际测试的包含桥梁振动信息的应变影响线采用不同次数的多项式进行拟合可得到更加准确的准静态影响线。
3 数值模拟
结合车-桥耦合振动模型进行数值计算,模拟不同行车工况下桥梁应变影响线提取问题。以3轴车辆行驶经过不同支撑边界桥梁时产生的桥梁动力响应(主要是动应变响应)为研究对象,结合已知车辆参数反演计算应变影响线,在此基础上对初始结果进行多项式分段拟合提取更加准确的影响线,并与理论值进行比较,研究不同行驶速度和路面不平度情况下的影响线提取问题。
3.1 算例1
以3轴车辆经过简支梁桥为例,研究简支边界条件下桥梁影响线提取。车辆模型及参数源于文献[15];桥梁模型参数如下:桥长Lb=16 m,抗弯刚度EI=4.36×109 N·m2,阻尼系数ξ=0.02,线密度 ρA=1.07×104 kg/m(ρ为梁密度,A为梁截面面积)。对汽车-桥梁耦合振动进行仿真分析时,参考国际标准ISO 8608[16]规定的路面不平度等级,通过对路面功率谱密度函数求傅里叶逆变换得到路面不平度。梁中心线距离底缘0.41 m,对桥梁1/4跨、1/2跨、3/4跨等截面处底缘测点(分别记为MP1,MP2和MP3)纵向应变影响线进行提取研究。
对3种工况(工况1:A级路面不平度,行车速度为18 km/h;工况2:A级路面不平度,行车速度为36 km/h;工况3:B级路面不平度,行车速度为72 km/h)进行计算分析,根据本文方法采用1次函数分段拟合影响线。在3种工况下MP1,MP2和MP3的动应变响应及影响线结果比较见图2~5。
从以上3种不同工况下的计算结果可以看出:反演计算提取的初始应变影响线(实测值)包含桥梁振动信息,尤其对于路面平顺性差、车辆行驶速度大的情况十分明显;对初始应变影响线进行分段拟合,拟合结果与理论值接近,能较好地消除桥梁振动的影响,且能适用于车辆行驶速度快、路面平顺性差的工况;当行车速度为72 km/h时,路面不平度为B级时的效果仍十分理想,这表明简支梁桥应变影响线标定测试具有可行性。
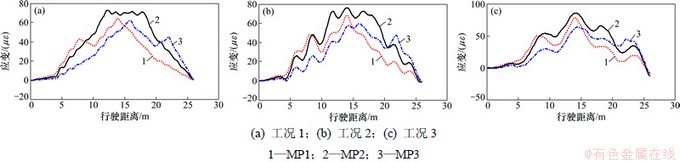
图2 不同行车工况下简支桥梁动力响应曲线
Fig. 2 Simply supported bridge dynamic response curves under different driving conditions
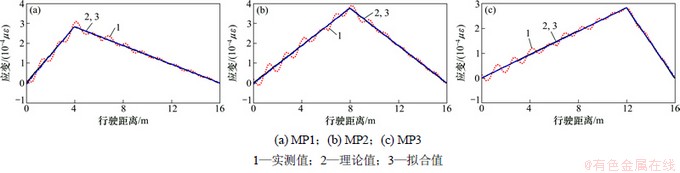
图3 工况1下简支梁桥不同测点影响线提取结果比较
Fig. 3 Simply supported beam bridge influence line extraction results of different measuring point under condition 1

图4 工况2下简支梁桥不同测点影响线提取结果比较
Fig. 4 Simply supported beam bridge influence line extraction results of different measuring point under condition 2
3.2 算例2
研究包含弹性扭转约束的简支梁桥影响线提取问题,模拟固定约束边界失效的情况。仍以3轴车辆过桥为例,除支撑边界外,车辆、桥梁参数、路面不平度规定及研究点位置均与前面的相同,桥梁模型见图1。两端转动约束刚度结合桥梁刚度取值,k1=k2=0.6e10,不同工况下梁桥的动力响应及不同测点影响线提取结果比较见图6~8。从图6~8可以看出:当桥梁支撑处存在转动弹性约束时,实测桥梁影响线与理论值接近程度比简支梁桥的高,但随着车辆速度的增大,路面不平度变差,初始曲线的波动逐渐明显。对初始结果采用三次多项式进行分段拟合得到的应变影响线与理论值接近,当行车速度为72 km/h、路面不平度为B级时,拟合结果仍十分理想,这表明弹性扭转约束边界条件下梁桥应变影响线标定测试的可行性。
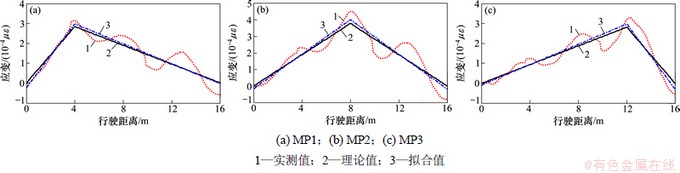
图5 工况3下简支梁桥不同测点影响线提取结果比较
Fig. 5 Simply supported beam bridge influence line extraction results of different measuring point under condition 3
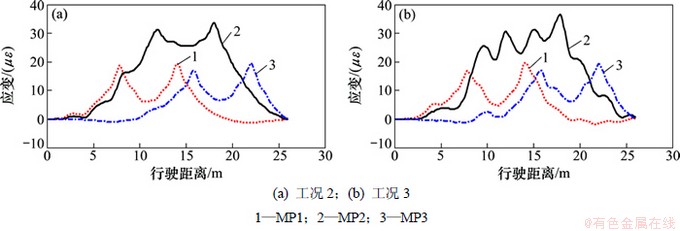
图6 弹性扭转约束梁桥不同行车工况下动力响应
Fig. 6 Elastically rotational restrained beam bridge dynamic response under different driving conditions
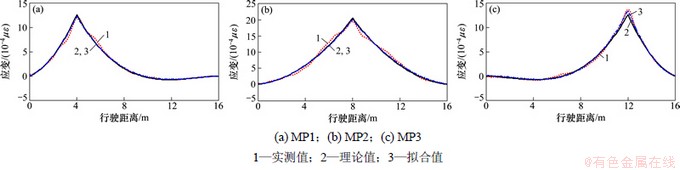
图7 工况2下弹性扭转约束梁桥不同测点影响线提取结果比较
Fig. 7 Elastically rotational restrained beam bridge influence line extraction results of different measuring point under condition 2
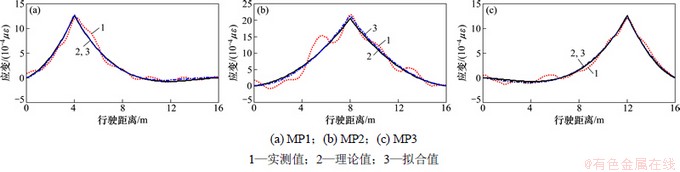
图8 工况3下弹性扭转约束梁桥不同测点影响线提取结果比较
Fig. 8 Elastically rotational restrained beam bridge influence line extraction results of different measuring point under condition 3
4 试验研究
以安徽省黄山市黄口大桥南岸桥为试验桥跨现场测试其应变影响线。试验桥跨20.0 m,由8片钢筋混凝土T梁组成,两端均为橡胶支座;桥面宽18.5 m,单幅,双向四车道,其车行道宽14.0 m,桥面铺装为混凝土。测试断面选在跨中及距北侧支座3.1 m处,有效的应变测点共4个,应变测点布置及现场测试结果见图9。
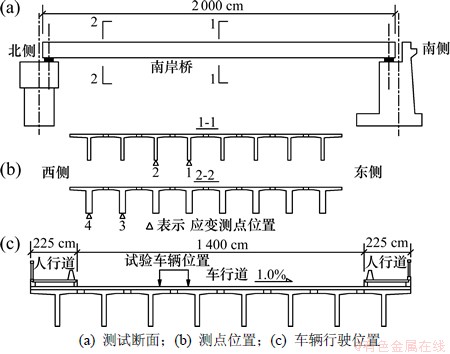
图9 测点及试验车辆布置
Fig. 9 Field test and arrangement of measuring points
试验车辆采用三轴重载车,其中1-2轴距为4.0 m,2-3轴距1.4 m,实测3轴重力分别为8.94×104,17.92×104和17.82×104 N。试验车辆分别以5,10,20和40 km/h共4种速度在西侧第2车道往返行驶。图10所示为2种不同行车速度下各测点动应变曲线。按照本文方法根据不同测点动应变曲线进行影响线拟合与提取,影响线动态测试结果如图11所示。
从图10~11可以看出:桥梁动力响应以及与之相对应的实测桥梁应变影响线受车辆行驶速度影响大;实测应变影响线虽然有着相同的基本趋势,但不同车辆速度下的测试结果包含不同程度的桥梁振动影响。在此基础上结合本文提出的方法,对初始结果进行3次多项式拟合,以进一步提取具有准静态特性的应变影响线,结果如图12~13所示。
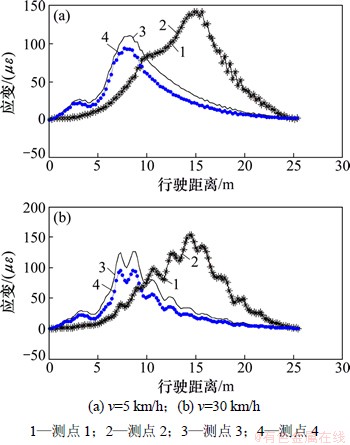
图10 测点动应变响应曲线
Fig. 10 Dynamic strain response curves of measuring points
由图12~13可知:通过多项式拟合提取的应变影响线较好地去除了桥梁振动的干扰,且在这4种行车速度下提取的影响线基本一致,有效克服了原始方法
在不同行车工况下得到不同影响线的弊端。受现场试验条件限制,5 km/h和40 km/h这2种行车速度分别因偏低和偏高而不能准确控制速度,这是引起偏差的主要原因;而10 km/h和20 km/h这2种工况下拟合提取的应变影响线较好吻合。从图13可以看出:实测同一截面不同测点的应变影响线仅存在幅值上的差异,不同截面测点的影响线则存在形状上的差异。截面1处测点1和测点2位于行车道正下方,与车辆横向距离差异不大,其幅值基本相同;截面2处测点3和测点4距离车辆横向位置差异较大,其影响线幅值明显不同。这体现了横向分布效应的影响,也进一步验证了试验结果的正确性和可靠性。
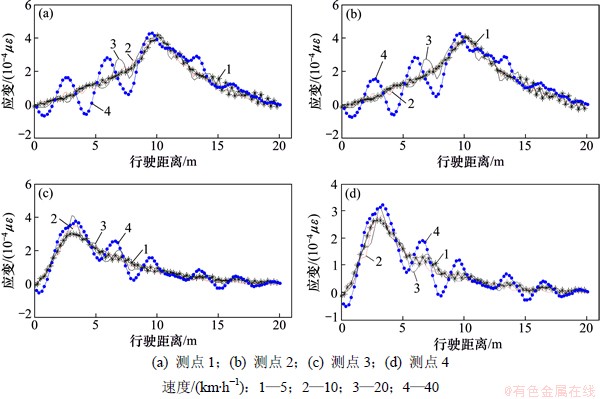
图11 不同速度下各测点应变影响线实测结果
Fig. 11 Strain influence line measured results of each measuring point under different speeds

图12 不同速度下测点应变影响线拟合结果
Fig. 12 Strain influence line fitting results under different speeds
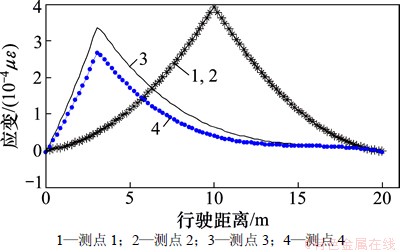
图13 不同测点应变影响线比较(v=10 km/h)
Fig. 13 Comparison of strain influence line for different measuring points (v=10 km/h)
5 结论
1) 对车辆过桥产生的桥梁动力响应进行反演计算得到桥梁初始影响线,在此基础上,采用多项式分段拟合的方法,能够剔除桥梁振动干扰因素的影响,提取具有准静态特性的桥梁应变影响线。
2) 通过拟合的方式提取应变影响线具有很高的精度。对理想简支梁桥,标定测试的初始影响线采用线性分段函数拟合,拟合曲线受桥梁振动的影响很小;采用三次多项式分段拟合弹性支撑和固支梁桥应变影响线时,较大的波动会在一定程度上影响拟合曲线形状,需界定合理的测试条件才能保证较高精度。
3) 不同行车速度下测试的初始应变影响线差别较大,但通过多项式拟合后输出的影响线一致,结果验证了本文算法的可行性。
参考文献:
[1] Strauss A, Wendner R, Frangopol D M, et al. Influence line-model correction approach for the assessment of engineering structures using novel monitoring techniques[J]. Smart Structures and Systems, 2012, 9(1): 1-20.
[2]  Comparison of techniques for damage identification based on influence line approach[C]//VIII International Congress: Machines, Technologies, Materials, Italy, 2011: 9-13.
Comparison of techniques for damage identification based on influence line approach[C]//VIII International Congress: Machines, Technologies, Materials, Italy, 2011: 9-13.
[3] Hirachan J, Chajes M. Experimental influence lines for bridge evaluation[J]. Bridge Structures, 2005, 1(4): 405-412.
[4] 唐光武, 廖敬波, 赵岩, 等. 基于影响线的桥梁结构评定理论研究进展[J]. 公路交通技术, 2008, 12(6): 39-43.
TANG Guangwu, LIAO Jingbo, ZHAO Yan, et al. Research advance of assessment theory for bridge structure based on influence line[J]. Technology of Highway and Transport, 2008, 12(6): 39-43.
[5] 李小年, 陈艾荣, 马如进. 桥梁动态称重研究综述[J]. 土木工程学报, 2013, 46(3): 79-85.
LI Xiaonian, CHEN Airong, MA Rujin. Review of bridge weigh-in-motion[J]. China Civil Engineering Journal, 2013, 46(3): 79-85.
[6] 王宁波. 非路面式桥梁动态称重理论与试验研究[D]. 长沙: 中南大学土木工程学院, 2013: 39-43.
WANG Ningbo. Non-pavement bridge weigh-in-motion: Theoretical and experimental study[D]. Changsha: Central South University. School of Civil Engineering, 2013: 39-43.
[7] Rowley C, Gonzalez A, O’Brien E J, et al. Comparison of conventional and regularized bridge-WIM algorithms[C]//Jacob B, O’Brien E J, Oconnor A. Proceedings of the International Conference on Heavy Vehicles. Paris: Wiley-ISTE, 2008: 221-230.
[8] O’Brien E J, Rowley C, Gonzalez A, et al. A Regularized Solution to the B-WIM Equations[J]. International Journal Heavy Vehicle Systems, 2009, 16(3): 310-327.
[9] 周建庭, 郝义, 沈小俊, 等. 递推迭代实测桥梁影响线原理及应用研究[J]. 公路交通科技, 2006, 23(6): 81-84.
ZHOU Jianting, HAO Yi, SHEN Xiaojun, et al. Study of bridge’s practical influence line from recurrence iterative testing and its use in bridge’s bearing capacity evaluation[J]. Technology of Highway and Transport, 2006, 23(6): 81-84.
[10] O’Brien E J, Quilligan M J, Karoumi R. Calculating an influence line from direct measurements[J]. Proceedings of the ICE-Bridge Engineering, 2006, 159(1): 31-34.
[11] Leng S S. Bridge influence line estimation for bridge weigh-in-motion system[J]. Journal of Computing in Civil Engineering, 2014. (DOI: 10.1061)
[12] Zhao H, Uddin N. Influence line calculation of existing bridges in BWIM system[C]//Proceedings of the IABSE-IASS Symposium. London, 2011: 572-580.
[13] Zhao H, Uddin N. Algorithm to identify axle weights for an innovative B-WIM system: Part Ⅰ[C]//Amin A, Okui Y, Bhuiyan A R. Proceedings of the IABSE-JSCE Joint Conference on Advances in Bridge Engineering: Ⅱ. Dhaka, Bangladesh, 2010: 527-536.
[14] Mcnulty P, O’Brien E J. Testing of bridge weigh-in-motion system in sub-arctic climate[J]. Journal of Testing and Evaluation, 2003, 31(6): 1-10.
[15] Zhu X Q, Law S S. Bridge dynamic responses due to road surface roughness and braking of vehicle[J]. Journal of Sound and Vibration, 2005, 282(3): 805-830.
[16] ISO 8608, Mechanical vibration-road surface profiles-reporting of measured data[S].
(编辑 陈灿华)
收稿日期:2014-04-10;修回日期:2014-06-22
基金项目(Foundation item):国家自然科学基金资助项目(51078357) (Project(51078357) supported by the National Natural Science Foundation of China)
通信作者:王宁波(1982-),男,湖北天门人,博士,讲师,从事桥梁结构健康监测及检测维护优化研究;电话:13787254800;E-mail:wangnb@csu.edu.cn