DOI: 10.11817/j.issn.1672-7207.2016.06.032
基于损伤特征向量谱的桩板式挡土墙损伤预警
徐乾1, 2,陈建功1, 2
(1. 重庆大学 土木工程学院,重庆,400045;
2. 重庆大学 山地城镇建设与新技术教育部重点实验室,重庆,400045)
摘要:对结构动力系统响应信号间的虚拟脉冲响应函数进行小波包分解得到小波包频带能量谱,引入剩余频带的概念,创建特征频带向量谱,并在特征频带向量谱的基础上构建损伤特征向量谱。当损伤特征向量谱为零向量时,挡土墙不存在损伤;当损伤特征向量谱为非零向量时,挡土墙存在损伤。为了量化挡土墙的损伤状态,提出2个损伤预警指标:能量比均方差DIS和能量比变异系数CIV。对某桩板式挡土墙进行锤击振动试验,通过损伤预警指标对不同损伤状态下的挡土墙进行损伤识别。研究结果表明:当DIS=0,CIV=0时,挡土墙不存在损伤;随着DIS和CIV的增大,挡土墙的损伤程度增大。因此,预警指标DIS和CIV不但可诊断挡土墙是否存在损伤,而且可识别挡土墙的损伤程度,可用于挡土墙结构的损伤预警。
关键词:损伤预警;挡土墙;特征频带向量谱;损伤特征向量谱;能量比均方差;能量比变异系数
中图分类号:TU311.41 文献标志码:A 文章编号:1672-7207(2016)06-2053-05
Damage alarming on pile plate retaining wall based on damage character vector spectrum
XU Qian1, 2, CHEN Jiangong1, 2
(1. School of Civil Engineering, Chongqing University, Chongqing 400045, China;
2. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Chongqing University,
Ministry of Education, Chongqing 400045, China)
Abstract: A wavelet packet frequency band energy spectrum was obtained using wavelet packet decomposition of virtual impulse response function between the response signals of structural dynamic system. The conception of residual frequency band was proposed, and character frequency band vector spectrum was also proposed. And the damage character vector spectrum was created based on the character frequency band vector spectrum. Retaining wall was undamaged when damage character vector spectrum was zero vector, while retaining wall was damaged when damage character vector spectrum was non-zero vector. In order to analyze the damage conditions of retaining wall quantitatively, two damage alarming indexes, i.e., energy ratio standard deviation (DIS) and energy ratio variation coefficient (CIV), were proposed. Through a hammer vibration test on a pile plate retaining wall, the damage condition of retaining wall was identified by damage alarming indexes. The results show that the retaining wall is undamaged when DIS=0, CIV=0. With the increase of DIS and CIV, the damage degree of the wall is also increased. So these alarming indexes based on damage character vector spectrum can not only distinguish whether the retaining wall is damaged or not, but also detect the damage degree of the wall. Consequently, the two indexes can be used to the damage alarming for retaining wall structures.
Key words: damage alarming; retaining wall; character frequency band vector spectrum; damage character vector spectrum; energy ratio standard deviation; energy ratio variation coefficient
挡土墙结构主要用于支撑土体、稳固边坡等,在建筑工程、交通工程和地下工程中都有广泛的应用。然而,由于存在材料缺陷、施工质量缺陷、材料老化等因素影响,损伤会在挡土墙内不断出现并积累,一旦损伤积累到一定程度,挡土墙就可能发生破坏。尤其是那些大型挡土墙结构,一旦发生破坏,其后果难以预料。如2008年的杭州地铁地下发生的连续墙坍塌事故,导致21人丧生,24人失踪,造成了恶劣的社会影响。鉴于此,对于挡土墙结构的健康预警或损伤预警是十分必要的。目前,国内外大多数损伤预警研究主要集中在结构构件[1]、建筑结构[2-3]和桥梁结构[4-5],而对于挡土墙这类支挡结构的损伤预警研究相对较少。本文作者以小波包频带能量谱分析理论为基础,引入小波包频带能量比谱的概念,并构建特征频带能量谱,在此基础上创建损伤特征向量谱,并提出2个损伤预警指标:能量比均方差(DIS)和能量比变异系数(CIV)。以某桩板式挡土墙为试验对象,对挡土墙的损伤进行预警。这为挡土墙结构的健康诊断技术提供一种新的研究思路和方法,对于我国防灾减灾工作也具有积极意义。
1 结构损伤预警方法
对于一个结构动力系统,其运动微分方程为
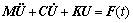 (1)
(1)
式中:M(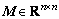 ),C(
),C(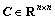 )和K(
)和K(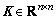 )分别为系统的质量矩阵,阻尼矩阵以及刚度矩阵;U(
)分别为系统的质量矩阵,阻尼矩阵以及刚度矩阵;U(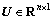 )与F(
)与F(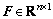 )分别为系统的位移矩阵和激励力矩阵。
)分别为系统的位移矩阵和激励力矩阵。
令状态向量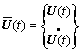 ,则运动微分方程可改写为
,则运动微分方程可改写为
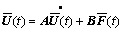 (2)
(2)
式中: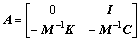 ;I为单位向量;
;I为单位向量;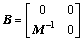 ;
; 。
。
目前的研究大都认为结构损伤的宏观表现是结构刚度被削弱[6-15],即结构刚度矩阵K降低。根据式(1),在恒定的外界激励作用下,结构刚度的变化必然引起结构动力响应变化。损伤预警技术的关键就是对结构的动力响应进行分析,然后进行损伤预警。
1.1 小波包频带能量比谱
根据结构动力系统的多尺度分解理论[16],对结构动力响应信号f进行i层小波包分解,在第i个分解层可以得到2i个子频带,则f可表示为
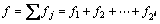 (3)
(3)
式中:fj表示第i层尺度空间上第j个子频带上的结构动力响应信号分量。第j个子频带上的结构响应信号分量fj的能量Ej可由下式计算:
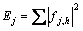 ;h=1,2,…,l (4)
;h=1,2,…,l (4)
式中:l为信号采样点个数。所以,结构动力响应信号f在第i层尺度空间上的小波包频带能量谱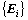 则可以表示为
则可以表示为
 (5)
(5)
式(5)所定义的小波包频带能量谱反映了结构动力响应信号的能量在各个频带上的分布。引入能量比Ig,对小波包频带能量谱进行归一化处理,即
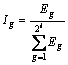 (6)
(6)
于是,响应信号f在第i层尺度空间上的小波包频带能量比谱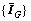 为
为
 (7)
(7)
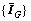 中能量比的排列是杂乱无章的,因此,先对频带能量比谱
中能量比的排列是杂乱无章的,因此,先对频带能量比谱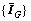 根据能量比由高到低进行排序,得到1个新的频带能量比谱
根据能量比由高到低进行排序,得到1个新的频带能量比谱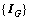 ,即
,即
 (8)
(8)
1.2 损伤特征向量谱
此外,受观测噪声的干扰,并不是所有频带能量比的变化都可以观测到。为了有效地反映能量比在频带上的变化,引入阈值ε(取0.85~0.95),且ε满足
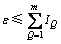 (9)
(9)
式中:IQ为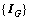 中第Q个能量比。通过ε可以确定
中第Q个能量比。通过ε可以确定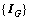 中前m个能量较大的频带,这m个频带上的能量比变化可用于识别挡土墙结构的损伤。除了
中前m个能量较大的频带,这m个频带上的能量比变化可用于识别挡土墙结构的损伤。除了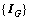 中的前m个频带外,剩余频带对损伤识别的贡献也是不容忽略的。所以,定义剩余频带的能量比Im+1为
中的前m个频带外,剩余频带对损伤识别的贡献也是不容忽略的。所以,定义剩余频带的能量比Im+1为
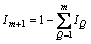 (10)
(10)
于是,定义特征频带向量谱{Ik}为
 (11)
(11)
这m+1个能量比对应的频带称为特征频带。
定义第k个特征频带的能量比差值DIk为
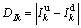 (k=1,2,…,m+1) (12)
(k=1,2,…,m+1) (12)
式中: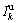 表示结构无损时第k个特征频带的能量比;
表示结构无损时第k个特征频带的能量比;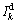 表示结构有损时第k个特征频带的能量比。于是,引入损伤特征向量谱DIk为
表示结构有损时第k个特征频带的能量比。于是,引入损伤特征向量谱DIk为
{DIk}=[DI1 DI2 … DIm DIm+1]T (13)
当挡土墙结构发生损伤时,损伤前后同一个特征频带的能量比会有差别,它使某些特征频带能量比减小,或使另外一些特征频带能量比增大。可以认为结构无损时的动力响应信号经过小波包变换得到的第k个特征频带对应的能量比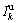 代表一种基准水平,而有损结构的动力响应信号经过小波包变换得到的第k个特征频带对应的能量比
代表一种基准水平,而有损结构的动力响应信号经过小波包变换得到的第k个特征频带对应的能量比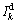 则围绕
则围绕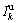 浮动。因此,损伤特征向量谱DIk可以用来刻画这种浮动程度。当DIk为零向量时,挡土墙结构没有损伤;当DIk为非零向量时,挡土墙结构存在损伤。于是,引入损伤预警指标,即
浮动。因此,损伤特征向量谱DIk可以用来刻画这种浮动程度。当DIk为零向量时,挡土墙结构没有损伤;当DIk为非零向量时,挡土墙结构存在损伤。于是,引入损伤预警指标,即
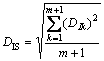 (14)
(14)
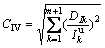 (15)
(15)
式中:损伤预警指标DIS和CIV都反映了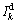 围绕
围绕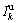 的波动程度,当DIS=0,CIV=0时,结构没有损伤;当DIS 和CIV不为0时,结构中存在损伤;而且DIS 和CIV越大,结构内的损伤也就越严重。因此,DIS和CIV可用于挡土墙结构的损伤预警。
的波动程度,当DIS=0,CIV=0时,结构没有损伤;当DIS 和CIV不为0时,结构中存在损伤;而且DIS 和CIV越大,结构内的损伤也就越严重。因此,DIS和CIV可用于挡土墙结构的损伤预警。
1.3 结构动力系统的虚拟脉冲响应函数
基于小波包频带能量谱的损伤特征向量,能够敏感地表征结构损伤而引起的结构动力特性的变化,但是小波包频带能量谱并不是结构的固有动力参数,它与结构外部的激励直接相关。当外部激励变化时,损伤指标也随之发生变化,具有较大的局限性。相关理论研究表明[16],在外界激励下,动力系统响应间的互相关函数可以表征结构的动力特性。丁幼亮等[17-18]通过研究认为:基于互相关函数的小波包频带能量谱仍具有一定的波动性和随机性。而基于虚拟脉冲响应函数的小波包频带能量谱却有很好的鲁棒性。因此,本文作者基于结构动力系统响应间虚拟脉冲响应函数的小波包频带能量谱,然后建立损伤特征向量,根据损伤预警指标实现对结构的损伤预警。
2 试验研究
某一混凝土桩板式挡土墙如图1所示。墙高为2.1 m,长为3.5 m,墙顶部厚为0.2 m,墙底厚为0.3 m,墙后填土为杂填土。为了约束挡土墙后填土的侧向变形,采取砖砌体来限制土体变形。为了模拟挡土墙的损伤,在完好挡土墙上开孔,然后用其他弹性模量较小的材料将孔洞重新浇筑。本文是在完好挡土墙墙面处开孔,孔洞长×宽为0.2 m×0.2 m,然后用其他材料(如砂浆、水泥净浆、石膏等)将孔洞重新浇筑,用来模拟存在损伤的挡土墙。定义无损挡土墙材料的弹性模量为Ec,定义填充材料的弹性模量为Es。为了表征损伤程度,引入ΔE,ΔE=Ec/Es。当ΔE=1时,挡土墙不存在损伤;随着ΔE的增大,损伤程度逐渐增加。
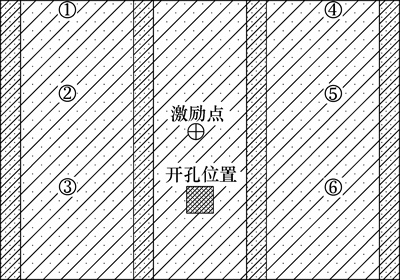
图1 桩板式挡土墙示意图
Fig. 1 Schematic diagram of pile plate retaining wall
试验时,在激励锤的激励下,挡土墙将产生动力响应。为了收集挡土墙的动力响应信号,在挡土墙上布置了6个无线加速度传感器(图1)。
根据上文提出的损伤预警方法,应求得结构动力系统响应间的虚拟脉冲响应函数,以1号和4号加速度传感器记录的响应信号为例。首先,提取1号和4号加速度传感器记录的加速度响应信号;然后,得到这2个响应信号间的虚拟脉冲响应函数;对虚拟脉冲响应函数进行小波包分解得到小波包频带能量谱;并构建特征频带向量谱,有损和无损挡土墙的特征频带向量谱如图2所示。由图2可知:有损挡土墙的能量比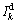 总是围绕无损挡土墙的能量比
总是围绕无损挡土墙的能量比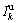 上下浮动,而且损伤程度越高,这种浮动程度也就越严重。图3所示为有损挡土墙的损伤特征向量谱,由图3可知:随着ΔE的增大,第k个特征频带的DIk也越大,此时,损伤程度也就越严重。为了量化挡土墙损伤程度,绘制DIS和CIV损伤走势曲线。
上下浮动,而且损伤程度越高,这种浮动程度也就越严重。图3所示为有损挡土墙的损伤特征向量谱,由图3可知:随着ΔE的增大,第k个特征频带的DIk也越大,此时,损伤程度也就越严重。为了量化挡土墙损伤程度,绘制DIS和CIV损伤走势曲线。
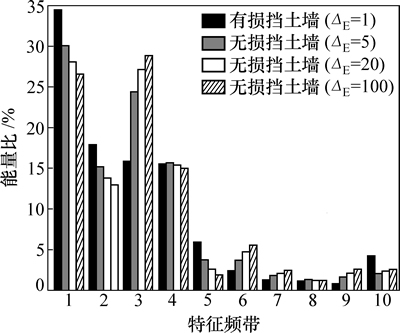
图2 有损和无损挡土墙的特征频带向量谱
Fig. 2 Character frequency band vector spectrum between undamaged retaining wall and damaged one

图3 有损挡土墙的损伤特征向量谱
Fig. 3 Damaged character vector spectrum of damaged retaining wall
分别求得1号和4号传感器、2号和5号传感器、3号和6号传感器记录响应信号的虚拟脉冲响应函数;然后,根据小波包频带能量谱损伤预警方法,建立损伤特征向量谱;最后,根据式(14)和式(15)求得不同损伤程度对应的损伤预警指标,并绘制DIS和CIV损伤走势曲线图,如图4和图5所示。由图4和图5可知:以曲线1为例,当ΔE=1时,DIS=0,CIV=0,此时挡土墙不存在损伤;当ΔE=1.25时,DIS=1.665 8,CIV =0.875;当ΔE=10时,DIS =4.184 6,CIV =1.967 2;当ΔE=100时,DIS =5.398 8,CIV =2.983 6。随着ΔE的增大,DIS和CIV也逐渐增大,表明损伤程度不断加深。分析曲线2和曲线3也可以得到相同的规律。
此外,1号和4号传感器布置在墙顶位置,其响应信号间虚拟脉冲响应函数的预警指标比较大,如图4和图5中的曲线3所示;而3号和6号传感器布置在接近墙底的位置,它们之间虚拟脉冲响应函数的预警指标则相对较小。如图4和图5中曲线1所示。因此,如果2个响应信号记录点的位置相对较高,其虚拟脉冲响应函数对应的预警指标也就比较大。
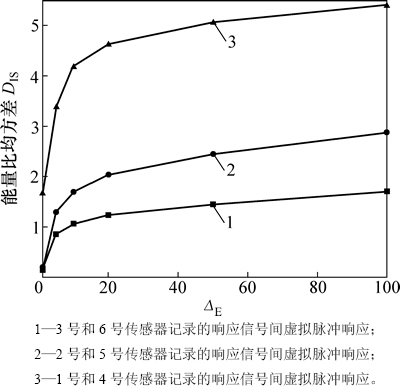
图4 不同损伤程度下的预警指标DIS
Fig. 4 Alarming index DIS under different damage degrees
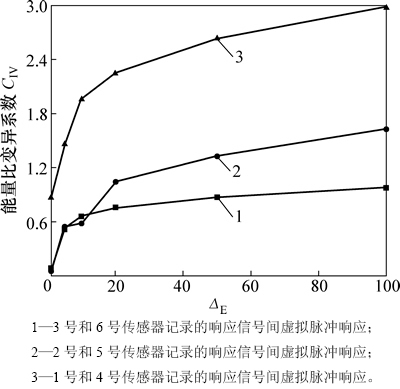
图5 不同损伤程度下的预警指标CIV
Fig. 5 Alarming index CIV under different damage degrees
3 结论
1) 对结构系统动力响应信号间的虚拟脉冲响应函数进行小波包变换,得到了小波包频带能量谱。引入小波包频带能量比谱的概念,考虑剩余频带的影响,创建特征频带向量谱,并构建损伤特征向量谱,提出2个损伤预警指标:能量比均方差DIS和能量比变异系数CIV。
2) 以一桩板式挡土墙为试验对象,用预警指标对挡土墙是否存在损伤以及损伤程度进行了损伤诊断。当DIS=0,CIV=0时,挡土墙不存在损伤;随着DIS和CIV的增大,挡土墙损伤程度增大。因此,损伤预警指标DIS和CIV不但可以判别挡土墙是否存在损伤,而且可以进一步诊断挡土墙的损伤程度。
3) 动力响应传感器的布置位置对损伤预警指标有较大影响,在实际运用时,建议将传感器布置在挡土墙顶部或较高的位置,这样将具有更好的预警效果。
参考文献:
[1] 高海洋, 郭杏林, 吴明勇. 基于频响函数虚部的板结构损伤检测方法研究[J]. 振动与冲击, 2012, 31(12): 86-91.
GAO Haiyang, GUO Xinglin, WU Mingyong. Damage detection for a plate based on imaginary part of frequency response function[J]. Journal of Vibration and Shock, 2012, 31(12): 86-91.
[2] KIM D G. Structural damage identification of a cantilever beam using excitation force level control[J]. Mechanical Systems and Signal Processing, 2010, 24(6): 1814-1830.
[3] PANIGRAHI S K, CHAKRAVERTY S, MISHRA B K. Damage identification of multistory shear structure from sparse modal information[J]. Journal of Computing in Civil Engineering, 2013, 27(1): 1-9.
[4] MEKJAVIC I. Damage identification of bridges from vibration frequencies[J].  Vjesnik, 2013, 20(1): 155-160.
Vjesnik, 2013, 20(1): 155-160.
[5] QU Weilian, SONG Wanjun, XIA Yong, et al. Two-step method for instability damage detection in tower body of transmission structures[J]. Advances in Structural Engineering, 2013, 16(1): 219-232.
[6] 郭杏林, 高海洋, 王盛辉. 一种基于频率响应曲率的损伤检测多步判定方法[J]. 工程力学, 2012, 29(7): 56-63.
GUO Xinglin, GAO Haiyang, WANG Shenghui. A multi-step decision method for damage detection based on frequency response curvature[J]. Engineering Mechanics, 2012, 29(7): 56-63.
[7] MERUANE V, HEYLEN W. A hybrid real genetic algorithm to detect structural damage using modal properties[J]. Mechanical Systems and Signal Processing, 2011, 25(5): 1559-1573.
[8] TURKER T, ALEMDAR S B. Vibration based damage identification of concrete arch dams by finite element model updating[J]. Computers and Concrete, 2014, 13(2): 209-220.
[9] AN Yonghui, OU Jinping. Experimental and numerical studies on model updating method of damage severity identification utilizing four cost functions[J]. Structural Control and Health Monitoring, 2013, 20(1): 107-120.
[10] 熊仲明, 王超, 林涛. 基于神经网络的大跨钢结构缺陷损伤的定位研究[J]. 振动与冲击, 2011, 30(9): 191-196.
XING Zhongming, WANG Chao, LIN Tao. Defect determination of large-span steel structure based on neural network[J]. Journal of Vibration and Shock, 2011, 30(9): 191-196.
[11] HATTORI G, SAEZ A. Damage identification in multi-field materials using neural networks[J]. Inverse Problems in Science and Engineering, 2013, 21(6): 929-944.
[12] NOBAHARI M, SEYEDPOOR S M. Structural damage detection using an efficient correlation-based index and a modified genetic algorithm[J]. Mathematical and Computer Modeling, 2011, 53(9): 1798-1809.
[13] SUNNY M R, KAPANIA R K. Damage detection in a pre-stressed membrane using a wavelet-based neuro fuzzy system[J]. AIAA Journal, 2013, 51(11): 2558-2569.
[14] 陈换过, 汪金寿, 李剑敏, 等. 基于提升小波包和神经网络的结构损伤检测[J]. 振动、测试与诊断, 2013, 33(1): 116-123.
CHEN Huanguo, WANG Jinshou, LI Jianmin, et al. Damage detection of wing-box based on lifting wavelet packet transform and neural network[J]. Journal of Vibration Measurement & Diagnosis, 2013, 33(1): 116-123.
[15] CHEN Jiangong, XU Qian, ZHANG Haiquan, et al. Damage identification of ribbed plate retailing wall based on damage character vector[J]. Electronic Journal of Geotechnical Engineering, 2014, 19: 3899-3908.
[16] XU Qian, CHEN Jiangong. Damage identification investigation on retailing wall structures[J]. Journal of Information and Computational Science, 2015, 12(13): 5119-5131.
[17] 丁幼亮, 李爱群, 邓扬. 面向结构损伤预警的小波包能量谱识别参数[J]. 东南大学学报(自然科学版), 2011, 41(4): 824-828.
DING Youliang, LI Aiqun, DENG Yang. Parameters for identification of wavelet packet energy spectrum for structural damage alarming[J]. Journal of Southeast University(Natural Science Edition), 2011, 41(4): 824-828.
[18] 丁幼亮, 李爱群. 基于小波包分析的Benchmark结构损伤预警试验研究[J]. 工程力学, 2008, 25(11): 128-134.
DING Youliang, LI Aiqun. Experimental research on structure damage alarming of Benchmark structure using wavelet packet analysis[J]. Engineering Mechanics, 2008, 25(11): 128-134.
(编辑 刘锦伟)
收稿日期:2015-06-03;修回日期:2015-08-11
基金项目(Foundation item):国家自然科学基金资助项目(51027004); 教育部长江学者和创新团队发展计划项目(IRT1045)(Project(51027004) supported by the National Natural Science Foundation of China; Project(IRT1045) supported by the Changjiang Scholars and Innovative Team Development Plan Project of National Ministry of Education)
通信作者:徐乾,博士,从事岩土工程结构健康检测研究;E-mail:xuqian0908140831@163.com