Trans. Nonferrous Met. Soc. China 22(2012) 288-298

 

Process forces and heat input as function of process parameters in AA5083 friction stir welds

 

Rajneesh KUMAR¹, Kanwer SINGH², Sunil PANDEY²

 

1. Engineering Division, National Metallurgical Laboratory, Jamshedpur 831007, India;

2. Mechanical Engineering Department, Indian Institute of Technology Delhi, Delhi 110016, India

 

Received 6 May 2011; accepted 2 August 2011

                                                                                                 

 

Abstract: AA5083 friction stir welds were produced using systematic experimental design, the process forces and heat input with varying parameters were studied. Helpful empirical models were developed in designing friction stir welding (FSW) tools and FSW welders. These models may be further helpful for making process parameter choice for this sort of alloy, defining welding program and control of process parameters by using computer numerical control friction stir welding welders. The results show that tool rotational speed, welding speed and tool shoulder diameter are most significant parameters affecting axial force and heat input, while longitudinal force is significantly affected by welding speed and probe diameter.

Key words: friction stir welding; AA 5083; tool design; heat input; process forces; process parameters

                                                                                                           

 

1 Introduction

 

Friction stir welding (FSW) invented and patented by THOMAS et al [1] is an important new welding technique with potentially significant application in the automotive and aerospace industry. With an extensive research on FSW during the last decade and its promising features, there has been a growing interest in the use of this technology in applications. Already some manufacturers have started using FSW particularly for low melting point alloys like aluminum, magnesium and dissimilar welding, but more are expected to join this group in future. Numbers of licenses issued by TWI every year are rising at an exponential rate.

Like any other manufacturing process, FSW also has certain important primary control parameters, such as tool rotational speed, welding speed, tool diameter and pin diameter. Response variables affected by these process parameters can be measured during the process. Some of these response variables are axial force, longitudinal and lateral force, spindle torque, heat input, tool temperature and etc. These variables in turn affect the final properties of weld joints. For efficient application of FSW process, it is necessary that all the important primary process parameters are identified and the effects on the process are characterized.

In the last few years, many studies have been carried out to relate the process parameters and their effect on output responses, and the main objective is to understand the fundamentals of the process. The effects of process parameters on FSW joints have been studied and reported. These studies include experimental as well as numerical and analytical modeling for optimization of process parameters to achieve desired joint properties. RUSSEL and SHERCLIFF [2] analytically modeled the microstructure in FSW joints and reported the effect of welding speed on final joint properties. ATHARIFAR et al and CAVALIER et al [3, 4] studied the effect of tool rotation and travel speed on the microstructure and mechanical properties of FSWed aluminum AA 6056 joints and optimized the process parameters. URSO et al [5] concluded that welding speed is a critical process parameter in their study on the effect of process parameters on aluminum AA6060 FS joints. The effect of process parameters on heat treatable aluminum AA2219 FS joints designed by experiments was reported by ARORA et al [6]. This study identified significant process parameters affecting process forces and tensile strength.

Some studies show that some process characteristics which can be measured during the process can be related

to the properties of FS welded joints. KUMAR and KAILAS [7] related axial load during FSW to tensile strength of FS welded joints. ARORA et al [8] investigated the torque, power requirement and stir zone geometry in FS welds. BALASUBRAMANIAN et al [9] related the effect of process forces to material flow and channeling in FSW. ROSE et al [10] studied the effect of axial force on microstructure and tensile properties of FS welds. CHOWDHURY et al [11] studied the effect of weld pitch on tensile properties. YU et al [12] related the effect of thermo-mechanical parameters to texture and tensile behavior of welds. It is shown that many studies could establish and relate process parameters during friction stir welding to final joint properties of welds. The responsible variables which can be precisely measured and monitored during welding are axial force, longitudinal force and heat input. These are proved to have direct relation with joint properties. Hence, monitoring them during the process can be used as a tool to control the subsequent quality of welds.

There have been few attempts to relate these process characteristics (axial load, longitudinal force and heat input) with the primary process parameters. ATHARIFAR et al [3] studied the effect of process parameters on loads during FSW using computational fluid dynamics model and validated the numerical models with experiment. NISHIHARA and NAGASAKA [13] studied the effect of tool rotational speed and welding speed on the tool and anvil temperatures. LIENERT et al [14] reported process forces and tool temperature as process response. JANDRIC et al [15] reported the effect of tool rotational speed and welding speed on the FS weld quality and temperature distribution. TANG et al [16] reported the effect of axial load and tool rotational speed on heat input and temperature distribution during FSW. JOHNSON [17] studied the effect of plunge depth, tool rotational speed and welding speed on process forces and torque. COLLIGAN et al [18] reported the effect of pin design, tool rotational speed and welding speed on process forces, torque, power and specific energy.  These studies help to understand FSW process better and acquire a lot of information about the process.

Till now, only few studies are available using statistical approach to relate primary process parameters in FSW with response variables via empirical relationship, which is helpful for welding engineers to program machines and to select a reasonable range of process parameters. One such attempt was made by RECORD et al [19], by identifying critical primary process parameters using statistical approach utilizing systematic design of experiments. But this study happens to be limited to the identification of critical parameters and no empirical relations have been suggested by the authors. This study attempted to use full factorial study of critical process parameters indicated already on the other monitorable process variables and tried to develop some empirical relationships using statistical approach.

2 Experimental

Al-Mg alloys are non heat-treatable type of aluminum alloys and AA5083 is very popular for exceptional performance in extreme environments. Although AA5083 has good weldability and is conventionally welded by gas shielded arc welding processes, but like other high strength aluminum alloys, this alloy also has problem of heat affected zone (HAZ) softness in strain hardened tempers as concluded by PANDEY [20]. Loss of strength in HAZ is inevitable and can only be controlled by controlling heat input during welding as reported by MATHERS [21]. DAVIS [22] reported the difficulty in getting mechanically and metallurgically compatible welded joints using beam welding processes, since high temperature encountered there leads to loss of some alloying elements. So, FSW is a candidate process suitable for this sort of alloys and is investigated in the study. Material AA 5083 H112 was used in the present study. Table 1 gives the chemical composition of the material. No specific work hardening treatment was given to the material, but some work hardening is received during extrusion. Such temper with no specific work hardening treatment given to material is classified under temper H112, providing that the resultant material properties satisfied the specified property range for this temper. The dimensions of the received plates were 12 mm×100 mm× 1000 mm.

Table 1 Chemical composition of experimental alloy

The welding trials were conducted on an adaptive milling machine with a 20 kW motor. Double-side welds were produced by butt-welding plates with dimensions of    250 mm×50 mm. These plates along with a steel backing plate were clamped to a load-measuring device, which in turn was suitably clamped to milling machine table. The total weld length was around 210 mm from pin entry to pin exit, with pin inserted at 15 mm and extracted at 225 mm from the leading plate edge, respectively. Computer numerical control (CNC) milling machine was used for making welds and weld process data was recorded for a total duration of 400 s for every run. For different weld runs, the parameters were changed in accordance with the design matrix, keeping secondary parameters like plunge speed constant. Tools used were made of H13 tool steel under heat treated condition. The tool shape was a flat shoulder with cylindrical pin having half of depth machined as an equilateral triangle (Fig. 1(a)). During welding, the machine head was tilted at an angle of 2° from the plate normal, so that the rear of the tool was lower than the front and had a shoulder plunge depth of 0.35 mm below the plate surface. The load measuring system (Figs. 1(b) and (c)) was capable of measuring upto 10 t vertical force with an accuracy of 2 kg       at a sampling rate of 50 samples per second while the X-direction force measuring capability of system was 2 t with accuracy of 0.4 kg at the same sampling rate. Machine power was measured by measuring the spindle motor current during welding and its comparison with calibration charts. Signal through various signal conditioning devices was interfaced with a PC using the 818HG data acquisition card and the results were saved as an excel spread sheet using a LabVIEW program. The welding direction was parallel to the extrusion direction of plates.

 

Fig. 1 Simulation diagram of tool shape (a), photo of load measuring system (b) and schematic diagram of load measuring system (c) of friction stir welding set up

32 plates were welded using four replications for a two-level full factorial design matrix. A full factorial design makes it possible to know the effect of all interactions along with primary process parameters on the process. Table 2 lists the design matrix of the trials, where ‘+’ stands for the higher level and ‘-’ stands for the lower level of the process parameters. The symbols of the process parameters used in the empirical derivations are given below Table 2. Table 3 details the higher and lower values of the process parameters. Factor levels were chosen from the known operational window that yielded apparently defect free welds. Such levels were also chosen so that the effects of parameters would be as apparent as possible.

 

Table 2 Design matrix and experimental results

Table 3 Welding parameters and their levels

3 Results and discussion

After completion of the trials according to the design matrix, the data of force and torque obtained through data acquisition system in the excel files are plotted and organized. Total data for each weld is collected for 400 s. A particular file contains the complete weld data including start delay, tool downward motion start period, pin plunging time, shoulder plunging, welding time, retracting time and end delay. For statistical analysis, only single data points per trial of experimental row are required. Hence, data for every response parameter is averaged in the welding period (starting from the longitudinal traverse of the tool) to obtain a single value for every response per trial run. 64 trials are made for the 4 replications of design matrix and 64 result files are prepared with this data. Average values of these readings are presented in tabular form in   Table 4.

Figure 2 shows the variation of X-force and Z-force and spindle torque with time for a typical weld run. Figure 2(a) shows the variation of Z-force with time. Total time is further divided to demarcate start delay, tool downward motion start period, pin plunging time, shoulder plunging, welding time, retracting time and end delay. Z-force increases steeply during plunging with the slope decreasing with time, indicating the softening of the material beneath FSW tool with heat generation. After complete plunging of pin, a sudden increase in force indicates the rubbing of tool shoulder with weld plate which also has a decreasing slope indicative of softening of material with heat generation. The Z-force increases momentarily at the start of welding feed but decreases subsequently, further, the reduction in force due to heating of the remaining portion of plate causes a pre-heating effect. Figure 2(b) shows the variations of X-force with respect to time. X-force is significant only for a certain time period, i.e., the welding feed time, during which tool exerts X-force on the clamped plates. Fluctuations in axial load and longitudinal X-force are attributed to the combination of work hardening and softening due to heat generation by ATHARIFAR et al [3] and SORENSEN and STAHL [23]. LIENERT et al [14] attributed these fluctuations to discrete stick-slip event experienced during welding. Figure 2(c) shows the variation of current, which is also representative of spindle torque, with respect to time. The asymmetric flow field around the tool due to combined rotation and linear motion of tool results in some lateral force on the tool, as reported by RAI et al [24]. A linear bearing constraining the motion of force table along welding path was used for measurement of X-force, so lateral force could not be recorded in this study and its effect on other forces was ignored.

3.1 Development of models

Selecting a model means to choose the form of the function and to write its equation. As the motive of the experiment is to have a general idea about how factors influence different response of the process and the process window is quite narrow, only two levels are selected for the experiment design. A simple linear regression model for two factorial experiments is expressed as

             (1)

 

 

Table 4 Observed values of torque index and forces

 

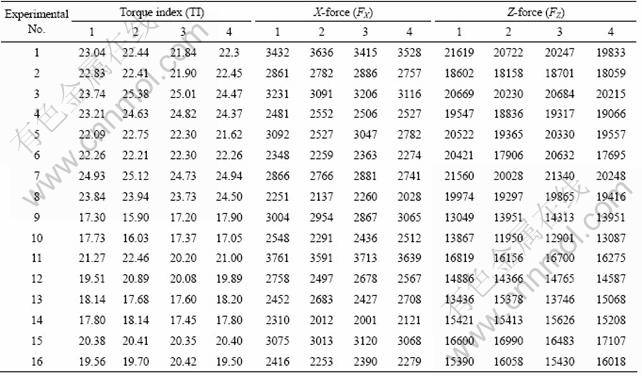
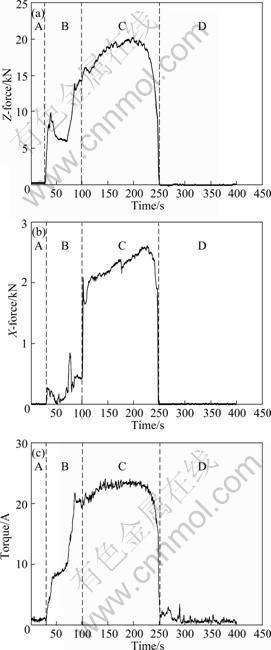
Fig. 2 Variation of forces and torque with time during welding: (a) Z-force; (b) X-Force; (c) Torque (Spindle motor current)

where β₁, β₂… are the regression coefficients; β₀ is the average response in factorial experiment; and ε is the random error component, which is has a mean value equal to 0 and a variance of σ². Like regression coefficients for main effect, coefficient β₁₂ corresponds to regression coefficient of interaction between factor x₁ and factor x₂ as mentioned by ANTONY [25]. As a full factorial design is selected for experimentation, model could have all possible interactions between factors. By replace x₁, x₂… with actual factors, the above model can be expressed as

              (2)

Models are made using coefficients for coded values of factors, where coded values can be determined as

                              (3)

where x_j is the coded value of the factor;  is the natural value of the factor;  is the natural value of the basic level or 0 level; J_j is the variation interval; and j is the number of factors. Coded values and variation intervals of factors are given in Table 3.

3.2 Evaluation of coefficients

For a two-level full factorial design selected for this experiment, the coefficients of selected models can be calculated using the equation below. This is based on the method of least squares:

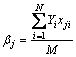                               (4)

where x_ji is the value of a factor or interaction in coded form; Y_j is the average value of the response parameter; M is the number of observations; and j=0, 1…, k, is the number of coefficients of the model.

For model preparation, statistical methods were used to ensure the homogeneity of variance of the data obtained. Coefficients obtained in models were checked for significance using student’s t test and the insignificant coefficients were dropped. After that final models were prepared. Developed models were checked for adequacy using statistical tools. Minitab 14 software was used for the analysis and to draw various plots.

 

3.3 Effect of various process parameters on X-force (F_X)

A representative plot of X-force in the course of welding is shown in Fig. 2(b). It can be seen in the representative plot that during plunging of tool, some X-force is experienced, which is of the order of 800 N in the representative plot and gradually increases with plunging and has a lot of fluctuations also. There is a sudden rise in the X-force during plunging as the tool shoulder touches the work-piece. X-force is experienced on the tool during plunging due to inclination of welding head in respect of table and due to the rotation of tool.  Data during welding period is averaged for statistical analysis. The developed model for the prediction of X- force after dropping the statistically insignificant coefficients is coded in the form as

F_X=2748+219d+146DN+326v                  (5)

Pareto plot showing the significant main effects and interactions in descending order of significance is shown in Fig. 3(a). Pin diameter (d) and welding speed (v) are the significant parameters affecting the F_X during FSW process. The interaction effect of tool shoulder diameter and tool rotational speed is also statistically significant during welding. The relationships between F_X and these parameters are shown in Figs. 3(b) and (c). Figure 3(d) shows the effect of the interaction of tool shoulder diameter and tool rotational speed on F_X.

It is clearly observed from the model that F_X increases with the increase in pin diameter. As shown in Fig. 3(b), F_X increases from 2529 to 2967 N with the increase in pin diameter of tool from 8 to 9 mm. It may be attributed to the more width of material that has to be sheared and stirred with increasing pin diameter of tool. Pin diameter is an important feature of tool geometry, and it plays an important role in creating resultant weld (by material flow and weld nugget) as well as in tool

design (tool pin must be strong enough to resist shear load during welding). F_X also increases with increasing welding speed. F_X rises from 2422 to 3073 N when welding speed is increased from 80 to 120 mm/min. This increase is even higher than the effect of pin diameter and is clearly evident from the developed model where the coefficient of welding speed is more than that of the pin diameter. SORENSEN and STAHL [23] reported the effect of process parameters on the longitudinal force in aluminum alloy AA 6061-T6. It is shown that longitudinal force is a strong function of pin length and approximately 50% longitudinal force is attributable to the shoulder. They also found that longitudinal force is a strong function of welding speed. RECORD et al [19] worked on the statistical identification of process parameters affecting FSW forces and studied the effect of tool RPM, welding speed, pin length and plunge depth on FSW forces. They found that welding speed is the most significant parameter affecting longitudinal force and other significant parameters affecting longitudinal force are pin length and tool rotational speed. But in this study, the effect of pin diameter was not studied.  JOHNSON [17] also observed a similar effect of welding speed on F_X during his studies on aluminum 6××× alloy. The reason for the increase in F_X is that as the welding speed increases, a higher amount of material is processed in the same unit time and this exerts more force on the tool, particularly in the longitudinal (welding) direction (Fig. 3(c)). Figure 3(d) shows that due to the interaction between parameters, at tool rotational speed of 500 r/min, F_X decreases with increasing shoulder diameter, while at rotational speed of 420 r/min, the effect of tool diameter on F_X is opposite. F_X can be assumed of having two components, namely, 1) shear force on tool pin due to material resistance to advancing tool and 2) frictional resistance experienced by tool shoulder moving in X direction during welding [23]. Observed trend in     Fig. 3(d) shows that at both rotational speed of tool, the increase in frictional resistance on tool is less significant than the decrease in shear force on tool pin due to a higher peak temperature of the weld. When the tool rotational speed is lower, then due to a lower welding temperature than that of the rotational speed weld, frictional resistance on tool shoulder increases more than the decrease in shear force which may be expected due to a higher heat input with the increase in tool diameter.

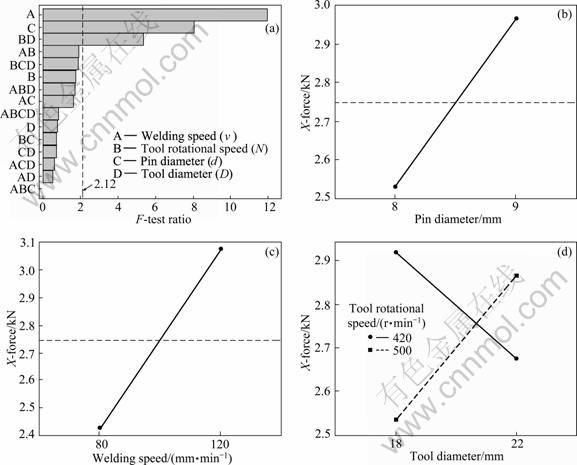
Fig. 3 Effect of process parameters on X-force: (a) Pareto chart; (b) Effect of pin diameter; (c) Effect of welding speed; (d) Interaction effect of tool diameter and rotational speed

 

3.4 Effect of various process parameters on Z-force (F_Z)

F_Z during welding is an important response which

determines the capability of machine to weld successfully. For a given machine, it is one of the most significant criteria to decide whether a material can be welded and up to what thickness it can be welded. ELANGOVAN and BALASUBRAMANIAN [26, 27] also concluded that inadequate F_Z can result in weld defects.

The developed model for the prediction of F_Z after dropping the statistically insignificant coefficients is coded as

F_Z =17412+2426D–551N+531v                  (6)

Pareto plot displaying the significant main effects and interaction in decreasing order of significance is shown in Fig. 4(a). It can be observed from the developed model as well as from Pareto diagram that tool shoulder diameter, tool rotational speed and welding speed are significant process parameters. No interaction is found to be significant. Effect of significant process parameters is shown in Figs. 4(b) to (d). Figure 4(b) shows the effect of tool shoulder diameter on F_Z. From the model, it is evident that the coefficient of tool diameter is maximum, hence it is the most significant parameter affecting F_Z. Z-force increases from 14.98 to 19.84 kN when the tool diameter increases from 18 to  22 mm. During the estimation of axial thrust, for selecting equipment, the following equation is considered

                                (7)

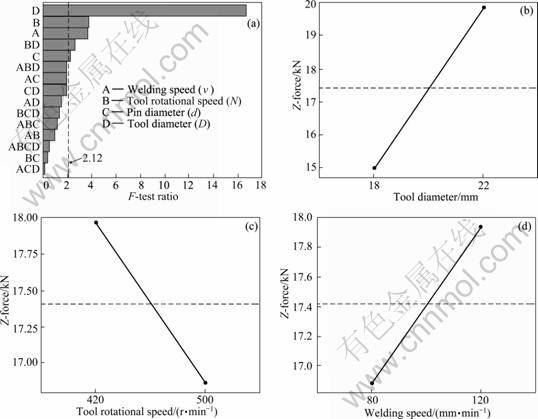
Fig. 4 Effect of process parameters on Z-force: (a) Pareto chart; (b) Effect of tool shoulder diameter; (c) Effect of rotational speed;  (d) Effect of welding speed

This equation indicates a strong dependence of axial thrust on tool diameter, hence increase in Z-force with increasing tool diameter is expected. However, this relationship gives a crude idea of the actual axial thrust during welding. According to Eq. (7), F_Z should increase by almost 1.5 times when the shoulder diameter is increased from 18 to 22 mm. But only 33% increase in F_Z is observed. This implies that some other factors affect the Z-force during the actual process. JOHNSON [17] also observed that Z-force increases with increasing tool shoulder diameter. Figure 4(c) shows the effect of tool rotational speed on Z-force. With increasing rotational speed from 420 to 500 r/min, F_Z decreases from 17.97 to 16.86 kN during welding. The decrease is caused by the higher peak temperature of the weld with increasing heat input (at higher tool rotational speed) which results in increasing softening of material beneath the tool, thereby decrease in flow stress of the material and lower F_Z. Figure 4(d) shows the effect of welding speed on Z-force, which has the least effect on F_Z. F_Z increases from 16.88 to 17.94 kN when welding speed is increased from 80 to 120 mm/min. PEEL et al [28] observed that Z-force increases with increasing weld pitch (which is the ratio of welding speed to tool rotational speed). These results are consistant with the result of this study.

 

3.5 Effect of various process parameters on heat input (HI) index

Heat input has always been considered an important parameter to assess the quality and characteristics of conventional fusion welds as mentioned by BANG et al [29]. LOMBARD et al [30] calculated the energy input to FS welds using two routes, namely, heat input approach and frictional power approach. Heat input is defined as the heat energy applied to the workpiece per unit length in the unit of kJ/mm. Heat input calculated with frictional power approach is not used as an effective coefficient of friction under the tool shoulder, which is difficult to determine under actual welding conditions. The equation given below is derived for heat input approach based on torque on tool during welding.

                               (8)

According to Eq. (8), heat input is directly proportional to torque and rotational speed and inversely to welding speed. With an appropriate efficiency of heat transfer, PEW [31] calculated that the heat input during welding can be calculated using current, rotational speed  and welding speed data. Heat input determines the metallurgical and mechanical characteristics of the weld joint as observed by LIENERT et al [32]. In this study, in the absence of absolute measurement of power, the term of heat input index is used as it is proportional to the actual heat input during welding.

The developed model for the prediction of heat input index after dropping the statistically insignificant coefficients is coded as

HI=100.73+10.90D+3.04N+2.46DN-19.05v-

2.15Dv-1.72Nv                          (9)

Pareto plot showing the significant main effects and interactions in decreasing significance order is shown in Fig. 5(a). It can be observed from the model that tool diameter, tool rotational speed and welding speed are the significant main effects. Three interaction effects were also found to be significant. Figure 5(b) shows the effect of tool shoulder diameter on heat input. Heat input index value raises from 89.2 to 111.6 when the tool diameter increases from 18 to 22 mm. With the increase in tool diameter, heat input increases expected as higher torque is exerted on a bigger tool. Similarly, increase in rotational speed from 420 to 500 r/min also causes the increase in heat input index value from 97.7 to 103.7, as shown in Fig. 5(c). The most significant parameter affecting heat input is welding speed which has a negative coefficient in the model. Thus, heat input index value decreases from 119.8 to 81.7 when welding speed increases from 80 to 120 mm/min. It is also shown graphically in Fig. 5(d). These effects of tool rotational speed and welding speed are expected because heat input is directly proportional to the rotational speed of the tool and inversely proportional to welding speed, as inferred in Eq. (8).

All these three significant factors have interactions and affect the heat input during welding. Figure 5(e) shows the interaction effect of tool shoulder diameter and tool rotational speed. For smaller tool diameter weld, effect of tool rotational speed is almost negligible, but when welding with bigger tool, this effect is quite significant. A good correlation exists between dynamic performance parameter and process characteristics. Lower frictional power occurs when the temperature during welding is high enough to give enough plasticization for required material flow as reported by LOMBARD et al [30]. The interaction in Fig. 5(e) shows that the peak temperature of small tool weld is higher than the peak temperature of weld made with bigger tool. Higher peak temperature causes softening of the material and reduction in torque, hence, the effect of increased rotational speed on the heat input is not so evident in small diameter tool.

Figure 5(f) shows the interaction effect of tool shoulder diameter and welding speed on heat input. At lower welding speed, effect of tool diameter on heat input is more significant than that at higher welding speed. Similarly, Fig. 5(g) shows the interaction of tool rotational speed and welding speed. It is evident again that at lower welding speed, the effect of tool rotational speed on heat input is more significant than that at higher welding speed.

 

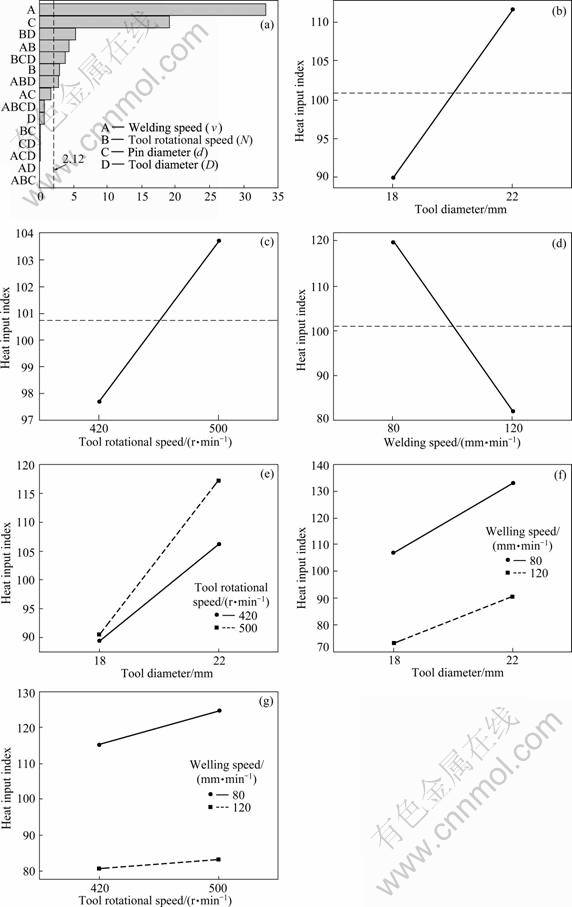
Fig. 5 Effect of process parameters on heat input: (a) Pareto chart; (b) Effect of tool shoulder diameter; (c) Rotational speed; (d) Welding speed; (e) Interaction effect of tool diameter and rotational speed; (f) Interaction effect of tool shoulder diameter and welding speed; (g) Interaction effect of rotational speed and welding speed

 

PEEL et al [28, 33] reported the effect of tool rotational speed and welding speed on heat input during FSW. It is observed that at higher welding speeds, the effect of tool rotational speed on the heat input is quite sight. While this effect of rotational speed on the heat input is more at significant lower welding speed. This is in a good agreement with our observations. In some earlier study, it was also found that welding speed had a very significant effect on the heat input at all tool rotational speeds. This is also in good agreement with our finding.

4 Conclusions

1) Tool speed, welding speed, tool shoulder diameter and probe diameter are critical process parameters affecting FSW process forces and heat input.

2) Axial thrust (Z-force) is most affected by tool diameter, rotational speed and welding speed. X-force is most affected by welding speed, pin diameter and interaction of tool diameter and rotational speed.

3) Heat input in FSW is affected by welding speed, tool diameter and rotational speed and their all possible two level interactions.

 

References

[1] THOMAS W M, NICHOLAS E D, NEEDHAM J C, MURCH M G, TEMPLE-SMITH P, DAWES C J. Friction stir butt welding: US 5460317 [P]. 1995.

[2] RUSSELL M J, SHERCLIFF H R. Analytical modelling of microstructure development in friction stir welding [C]//Proceedings of the First International Symposium on Friction Stir Welding. Thousand Oaks, California, USA, 1999.

[3] ATHARIFAR H, LIN D, KOVACEVIC R. Numerical and experimental investigations on the loads carried by the tool during friction stir welding [J]. Journal of Materials Engineering and Performance, 2009, 18(4): 339-350.

[4] CAVALIERE P, CAMPANILE G, PANELLA F, SQUILLACE A. Effect of welding parameters on mechanical and microstructural properties of AA6056 joints produced by friction stir welding [J]. Journal of Materials Processing Technology, 2006, 180: 263-270.

[5] URSO G D, CERETTI E, GIARDINI C, MACCARINI G. The effect of process parameters and tool geometry on mechanical properties of friction stir welded aluminium butt joints [J]. International Journal of Material Forming, 2009, 2(1): 303-306.

[6] ARORA K S, PANDEY S, SCHAPER M, KUMAR R. Effect of process parameters on friction stir welding of aluminum alloy 2219-T87 [J]. International Journal of Advanced Manufacturing Technology, 2010, 50: 941-952.

[7] KUMAR K, KAILAS S V. On the role of axial load and the effect of interface position on the tensile strength of a friction stir welded aluminium alloy [J]. Materials & Design, 2008, 29(4): 791-797.

[8] ARORA A, NANDAN R, REYNOLDS A P, DEBROY T. Torque, power requirement and stir zone geometry in friction stir welding through modelling and experiments [J]. Scripta Materialia, 2009, 60(1): 13-16.

[9] BALASUBRAMANIAN N, MISHRA R S, KRISHNAMURTHY K. Process forces during friction stir channelling in an aluminum alloy [J]. Journal of Materials Processing Technology, 2011, 211(2): 305-311.

[10] ROSE A R, MANISEKAR K, BALASUBRAMANIAN V. Effect of axial force on microstructure and tensile properties of friction stir welded AZ61A magnesium alloy [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(5): 974-984.

[11] CHOWDHURY S M, CHEN D L, BHILE S D, CAO X. Tensile properties of a friction stir welded magnesium alloy: Effect of pin tool thread orientation and weld pitch [J]. Materials Science and Engineering A, 2010, 527(21-22): 6064-6075.

[12] YU Z Z, CHOO H, FENG Z L, VOGEL S C. Influence of thermo-mechanical parameters on texture and tensile behavior of friction stir processed Mg alloy [J]. Scripta Materialia, 2010, 63(11): 1112-1115.

[13] NISHIHARA T, NAGASAKA Y. Measurement of tool temperature during friction stir welding [C]//Proceedings of 4th International Symposium on Friction Stir Welding. Park City, 2003.

[14] LIENERT T J, Jr STELLWAG W L, GRIMMETT B B, WARKE R W. Friction stir welding studies on mild steel [J]. Welding Journal, 2003, 82(1): s1-s3.

[15] JANDRIC D, OUYANG J H, VALANT M, KOVACEVIC R. On-line weld quality diagnostics in FSW [C]//Proceedings of 11th International Conference on Computer Technology in Welding. Columbus, OH, 2001: 173-181.

[16] TANG W, GUO X, MCCLURE J C, NUNES A C. Heat input and temperature distribution of friction stir welds [J]. Journal of Materials Processing and Manufacturing Science, 1999, 7(2): 162-172.

[17] JOHNSON R. Forces in friction stir welding of aluminium alloys [C]//Proceedings of 3rd international symposium on friction stir welding. Kobe, Japan, 2002.

[18] COLLIGN K J, XU J, PICKENS J R. Welding tool and process parameters effect in friction stir welding of aluminium alloys [M]. Pennsylvania: TMS, 2003: 181-190.

[19] RECORD J H, COVINGTON J L, NELSON T W, SORENSEN C D, WEBB B W. A look at the statistical identification of critical process parameters in friction stir welding [J]. Welding Journal, 2007, 86(4): s97-s103.

[20] PANDEY S. Some studies on MIG welding of aluminium and its alloy 5083[D]. New Delhi: Indian Institute of Technology, 1986.

[21] MATHERS G. Welding of aluminium and its alloys [M]. Cambridge: Woodhead Publishing Ltd, 2002: 147.

[22] DAVIS, J R. Aluminum and aluminum alloys [M]. Ohio: ASM International, 1994: 376.

[23] SORENSEN C D, STAHL A L. Experimental measurements of load distributions on friction stir weld pin tools [J]. Metallurgical and Materials Transactions B, 2007, 38: 451-459.

[24] RAI R, DE A, BHADESHIA H K D, DEBROY T. Review: Friction stir welding tools [J]. Science and Technology of Welding and Joining, 2011, 16(4): 325-342.

[25] ANTONY J. Design of experiments for engineers and scientists [M]. Oxford: Butterworth-Heinemann, 2003: 1-5.

[26] ELANGOVAN K, BALASUBRAMANIAN V. Influences of pin profile and rotational speed of the tool on the formation of friction stir processing zone in AA2219 aluminium alloy [J]. Materials Science and Engineering A, 2007, 459: 7-18.

[27] ELANGOVAN K, BALASUBRAMANIAN V. Influences of tool pin profile and tool shoulder diameter on the formation of friction stir processing zone in AA6061 aluminium alloy [J]. Materials and Design, 2008, 29(2): 362-373.

[28] PEEL M J, STEUWER A, WITHERS P J, DICKERSON T, SHI Q, SHERCLIFF H. Dissimilar friction stir welds in AA5083-AA6082. Part I: Process parameter effects on thermal history and weld properties [J]. Metallurgical and Materials Transactions A, 2006, 37: 2183-2193.

[29] BANG K S, PARK C, CHANG W S, PARK C G, CHUNG W H. Influence of heat input on mechanical properties of multipass low-alloy steel weld metal [J]. Materials Science Forum, 2008, 580-582: 17-20.

[30] LOMBARD H, HATTINGH D G, STEUWER A, JAMES M N. Optimising FSW process parameters to minimise defects and maximise fatigue life in 5083-H321 aluminium alloy [J]. Engineering Fracture Mechanics, 2008, 75: 341-354.

[31] PEW J W. A torque-based weld power model for friction stir welding [D]. Brigham Young University, Utah, USA, 2006.

[32] LIENERT T J, GOULD J E, STOTLER T, LAPOLLA D S. Friction stir welding of mild steels [C]//AWS Convention Abstracts. Miami, USA: AWS, 1999: 219-220.

[33] PEEL M J, STEUWER A, WITHERS P J. Dissimilar friction stir welds in AA5083-AA6082. Part II: Process parameter effects on microstructure [J]. Metallurgical and Materials Transactions A, 2006, 37: 2195-2205.

()

AA5083铝合金的搅拌摩擦焊接工艺参数对

搅拌头受力和热输入的影响

 

Rajneesh KUMAR¹, Kanwer SINGH², Sunil PANDEY²

 

1. Engineering Division, National Metallurgical Laboratory, Jamshedpur 831007, India;

2. Mechanical Engineering Department, Indian Institute of Technology Delhi, Delhi 110016, India

摘  要：采用系统实验设计方法研究AA5083铝合金搅拌摩擦焊接工艺参数对搅拌头受力和热量输入的影响，得到了用来设计搅拌摩擦焊搅拌头和焊机的经验模型。当采用计算机来控制搅拌摩擦焊接时，这些模型可用来确定AA5083这类铝合金的摩擦焊接工艺参数、编制焊接程序及工艺参数控制。结果表明：影响轴向力和热量输入的重要参数是搅拌头转速、焊接速度和搅拌头轴肩直径，而影响纵向应力的重要参数是焊接速度和探头直径。

关键词：搅拌摩擦焊；AA 5083合金；搅拌头设计；热量输入；受力；工艺参数

 (Edited by FANG Jing-hua)

Corresponding author: Rajneesh KUMAR; Tel: +91-657-2345034; Fax: +91-657-2345213; E-mail: rkgupta@nmlindia.org

DOI: 10.1016/S1003-6326(11)61173-4