Trans. Nonferrous Met. Soc. China 23(2013) 3448-3455

Fluidized-bed chlorination thermodynamics and kinetics of Kenya natural rutile ore

Li-ping NIU^1,2, Ting-an ZHANG^1,2, Pei-yuan NI^1,2, Guo-zhi ^1,2, Kingsam OUYANG³

1. School of Materials and Metallurgy, Northeastern University, Shenyang 110819, China;

2. Key Laboratory for Ecological Utilization of Multimetallic Mineral (Ministry of Education), Northeastern University, Shenyang 110819, China

3. Hunan Research Institute for Nonferrous Metals, Changsha 410100, China

Received 15 July 2013; accepted 30 September 2013

Abstract: Natural rutile and gaseous chlorine with carbon as reductant were used to prepare titanium tetrachloride.

1173Kesing C uctant,  Thermodynamics and kinetics of chlorination of Kenya natural rutile particles in a batch-type fluidized bed were studied at 1173-1273 K. Thermodynamic analysis of this system revealed that the equation of producing CO was dominant at high temperatures. Based on the gas-solid multi-phase reaction theory and a two-phase model for the fluidized bed, the mathematical description for the chlorination reaction of rutile was proposed. The reaction parameters and the average concentration of gaseous chlorine in the emulsion phase were estimated. The average concentration of emulsion phase in the range of fluidized bed was calculated as 0.3 mol/m³. The results showed that the chlorination of natural rutile proceeded principally in the emulsion phase, and the reaction rate was mainly controlled by the surface reaction.

Key words: natural rutile; thermodynamics; kinetics; gas-solid reaction; fluidized bed; two-phase model

1 Introduction

Titanium tetrachloride (TiCl₄) has been widely utilized as intermediate materials for producing titanium white (TiO₂) and titanium sponge that are two major products in titanium industry. In the production of TiO₂ pigment by the chloride process, TiCl₄ is produced by the high temperature fluidized bed chlorination of TiO₂. In China, at least 90.5% (by mass) of the titanium resources are located in Panzhihua, belonging to magnetite with high contents of CaO and MgO. Chlorination of TiO₂ occurs at high temperatures in the temperature range from 1073 to 1373 K, and it is a stable chloride. At these temperatures impurities are also chlorinated, which requires high-quality materials such as rutile, synthetic rutile, or TiO₂-rich slag [1].

BARIN and SCHULER [2] studied the chlorination of pure titanium dioxide by putting TiO₂ and coke into a reactor side by side. It was concluded that the chlorination rate of TiO₂ with TiO₂-C contact was faster 40-50 times that in the absence of carbon and, the acceleration of chlorination decreased with TiO₂ and carbon separating. YANG and HLAVACEK [3] studied the chlorination kinetics of titanium dioxide (rutile and anatase) with coke and carbon monoxide being reductant in a fixed-bed reactor at 1073-1273 K. When C was used as reductant, a solid-solid reaction was involved. Reactivity was highly enhanced by solid carbon and it was concluded that an activated C-TiO₂-Cl complex contributed to the enhanced reactivity. A reaction model based on phase boundary control could be applied to the experimental data.

BERGHOLM [4] chlorinated Australian rutile in the presence of CO and carbon and suggested a rate- controlling reduction step, followed by rapid chlorination of the reduced rutile. The chlorination rate of C-Cl₂ system was much higher than that on the CO-Cl₂ system. In addition, the reaction rate with carbon being reductant was dependent on Cl₂ concentration, but not CO. YOUN and PARK [5], ZHOU and SOHN [6] developed a mathematical model of fluidized-bed chlorination of rutile. However, kinetic data of carbochlorination of Kenya nature rutile ores were not readily available in the literature.

As a part of optimizing plant operation, a laboratory study on the chlorination rates of Kenya natural rutile ore was carried out for coke as reducing agents. In our study, chlorination of rutile ore (powder, <150 μm, 93.29%) was carried out. Temperatures of 1073-1273 K were chosen as reaction temperatures. The total pressure of 102.1 kPa inside the reactor was kept. The combinations of chlorine with solid carbon were used for chlorination. The main objective of this study is to understand the carbochlorination process of nature rutile by analyzing the intrinsic kinetics and the effect of other factors on the process, and to provide rate expression and other kinetic data for design and scale-up purposes.

2 Thermodynamic analysis

The following two main reactions take place in the boiling chlorination process of rutile:

TiO₂+C+2Cl₂=TiCl₄+CO₂                           (1)

TiO₂+2C+2Cl₂=TiCl₄+2CO                    (2)

The corresponding Gibbs free energy of rutile carbochlorination can be described by the following equations.

or

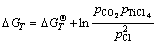                    (3)

Under normal operating conditions, for the above two formulas, 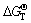<0, so the reactions (1) and (2) can be spontaneous. Formulas may be seen as the compound expression of the Boundouard reaction and TiO₂-C-Cl₂ reaction system. Suppose that the probability of generating CO reaction is η, η=(p_CO/2)/(p_CO/2+p_CO2), the actual production of η can be varied within a very wide range of 0.01-0.99. The above two equations can be jointly expressed as

TiO₂+(1+η)C+2Cl₂=TiCl₄+2ηCO+(1-η)CO₂           (4)

The composition of furnace gas is complex in carbochlorination process, containing CO, CO₂, TiCl₄, Cl₂, and COCl₂. Under normal boiling chlorinated conditions, CO/CO₂ volume ratio is not only a reflection of the reaction mechanism in the chlorination process, but also an important index of chlorination process stability [3,7-9].

When calculating the Gibbs free energies of the nature rutile carbochlorination reactions, it is known from reaction (4) that, under certain TiCl₄ partial pressure p_TiCl4, from (2+η)p_TiCl4≤101.325 kPa, the η range for thermodynamic calculation can be determined. The results are shown in Figs. 1-3, where η values are 0.2, 0.4, 0.5 and 0.7; temperatures are 900, 1000, 1100, 1200, 1300 and 1400 K; partial pressures of TiCl₄ (φ) are 0.1, 0.2, 0.3, 0.35, 0.4 and 0.45; the exhaust pressure is 101.325 kPa.

Results of thermodynamic calculations are given in Figs. 1 under different TiCl₄ partial pressures. Equation (2) is dominant at high temperatures. This result is consistent with YOUN’s analysis conclusion by thermodynamic equilibrium theory [5]. The same trend of calculating result for Fe₂O₃-C chloride system is observed (see Figs. 2 and 4).

In the vent gas, the contents of Cl₂, COCl₂ and other impurities are rarely, and the content of chlorine is less than 1%. For the chlorination reaction of impurity oxides, standard Gibbs free energy of oxides carbochlorination reaction shows that chlorination reaction capacity of Fe₂O₃ is greater than that of TiO₂.

In the case of little content of oxide impurities, the chlorinate gas partial pressure is less than that of the titanium tetrachloride, and ΔG_T of above oxide chlorination reaction is more negative than ΔG_T of TiO₂ chlorination reaction under the same system. Thus the reactions are more complete. The greater the ratio η to generate the CO reaction is, the greater the reaction affected by temperature is. The Gibbs free energy of reaction is more negative at the high temperatures. Meanwhile, with the ratio of η increasing, the impact of product TiCl₄ partial pressure on the Gibbs free energy of the reaction tends to decrease. When η is smaller, the impact of partial pressure of product TiCl₄ on the Gibbs free energy of the reaction is greater.

3 Experimental

A laboratory scale fluidized-bed reactor consisted of a quartz tube (outer diameter 60 mm, wall thickness 2.5 mm, and length 1000 mm) that was placed in a self-made tube furnace equipped with a temperature controller. A porous disc divided the reactor into two sections, supporting the bed and distributing the fluidizing gas uniformly. The gases were metered through rotameters, mixed, then entered the lower section of the reactor where they were preheated. The product gases were cooled in a condenser, then passed through two carbon tetrachloride scrubbers, which removed the TiCl₄ and other metal chlorides. The unreacted chlorine was absorbed in a caustic soda scrubber system.

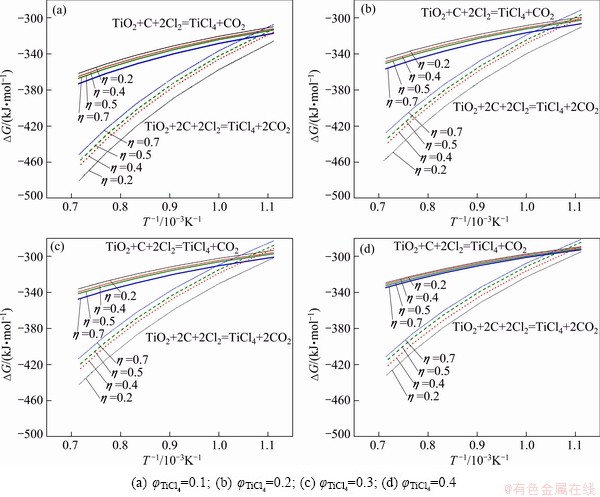
Fig. 1 Gibbs free energy change curves of TiO₂+2C+2Cl₂=TiCl₄+2CO and TiO₂+C+2Cl₂=TiCl₄+CO₂

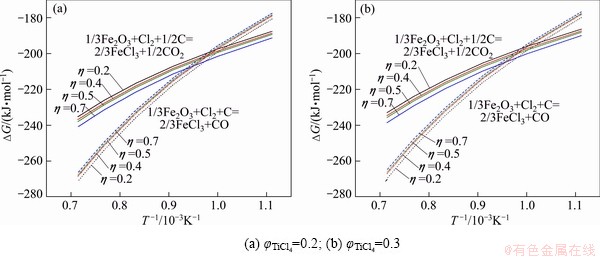
Fig. 2 Gibbs free energy change curves of 1/3Fe₂O₃+Cl₂+C= 2/3FeCl₃+CO and 1/3Fe₂O₃+Cl₂+1/2C=2/3FeCl₃+1/2CO₂ (FeCl₃ at partial pressure of 2 kPa)

The procedure usually followed was to preheat the empty reactor to 1073 K, then continue heating while fluidizing the bed material with nitrogen. When the operating temperature measured by a thermocouple immersed in the fluidized bed stabilized for 5 min at the desired value, the nitrogen flow was discontinued and the predetermined gas mixture (pure chlorine gas) passed through the reactor for a specified period of time. At the end of the run, the bed material was allowed to cool to 773 K while being purged with nitrogen. For samples of oxide mixed with carbon, The conversion rate of TiO₂, χ, is calculated by the following equation:

where m_slag is the chloride slag mass; m_TiO2-slag is the TiO₂ content in slag; m_rutile is the natural rutile mass; m_TiO2-slag is the TiO₂ content in rutile.

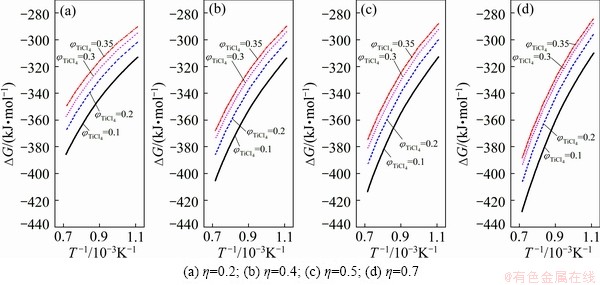
Fig. 3 Gibbs free energy change curves of Eq. (4)

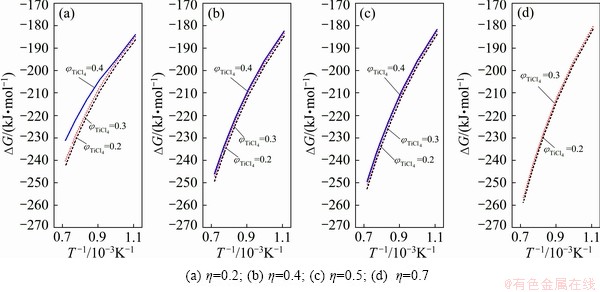
Fig. 4 Gibbs free energy change curves of 1/3Fe₂O₃+Cl₂+(1+η)/2C=2/3FeCl₃+ηCO+(1-η)/2CO₂

The average particle size of Kenya natural rutile was 187.234 μm. The particles can be fluidized by smaller gas flow. The coke was a petroleum-derived material with LOI of 94.94%. The total gas flow rate was determined to be 4 times as much as the minimum fluidizing velocity in order to make the materials mix completely and temperature uniform within the bed, and not cause excessive carryover of fine solids. The flow rate was approximately 0.036 m³/h, and the initial mass of ore was 200 g.

Particle size and morphologies were characterized by scanning electron microscope (SEM, Model JSM- 6360LA, NEC), and micromeritics instrument (Norcross, GA), respectively.

4 Mathematical model of gas-solid reaction in fluidized bed

SEM micrographs of Kenya natural rutile particles at different chlorination times are shown in Figs. 5(a) and (b). The results, which have been confirmed in the previous study, indicate that Kenya rutile is a nonporous solid which does not undergo internal chlorination. Therefore, the reaction occurs exclusively on the surface of the particles.

In a batch-type fluidized bed, the fractional reaction of each fluidized particle is presumed to be uniform when the particles with the same size are fed to the reactor at the same time. The following assumptions were made on the chlorination of a single nature rutile particle at 1073-1323 K.

Since the products are in gaseous state and no ash is formed on the surface of the solid particles during reaction, the reacting particle shrinks as the reaction is going on, and finally disappears. The reaction can be summarized as the following three steps: 1) Diffusion of gaseous reactants, by which Cl₂ goes through the gas film from the bulk of the gas stream to the surface of the nature rutile solid particle; 2) Reaction of gaseous reactants Cl₂ with the solid rutile particle on the solid surface; 3) Diffusion of reaction products, by which TiCl₄ and CO₂ go through the gas film from the surface of the solid into the bulk of the gas stream.

Fig. 5 SEM images of chloride slag

To determine the intrinsic kinetics, the reaction conditions were chosen such that the mass transfer (steps 1 and 3) did not control the overall reaction rate. A small amount of sample and high gaseous flow rate are required for that. Flow amount is determined by experiment. In this study, the resistance of mass transfer is neglected, and chemical reaction becomes the sole rate-limiting step (step 2). In this case, the chemical reaction in the model of shrinking unreacted solid particle was considered the rate-controlling step.

Assuming that the reaction is an irreversible one-order reaction and the rutile particle is spherical. Based on the above assumptions, the rate equation for each sequential step is

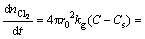
            (5)

Then the overall rate equation is

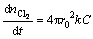                            (6)

where

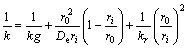              (7)

and by the chemical reaction equation (1)，following equation are obtained.

After integration of the above equation, we have the formula of the chlorination rate and time.

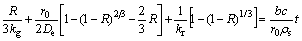    (8)

Based on a two-phase model for the fluidized bed, the fluidizing air stream blown into the bed from the bottom is divided into two portions. One portion of fluidizing gas flows through the emulsion phase at a critical velocity u_mf and a uniform and continuous emulsion phase (E) with particles forms. The remainder rises through the bed in the form of gas bubbles whose volume fraction in the bed is δ. A mass balance with regard to the fluidizing gas yields the following equation: mass transfer between emulsion phase and gas bubbles phase [10,11].

In order to derive the mass balance equation for Cl₂ gas in the fluidized bed, the following two assumptions are made: 1) The fluidized particles are completely mixed within the bed, and the upward gas flow through each phase is in plug flow; 2) The flow rate of fluidizing gas is constant along the height of bed; (3) Due to the small amount of reactant, we can ignore the volume changes of gas caused by gas-solid reaction along the bed height; 4) We ignore the effect of the temperature and concentration change in the fluidized bed radially and the effect of fluidized bed wall.

Using the fluidized bed cross section S for the bottom, taking sectional micro-element along the height of bed dz, we can get a differential equation dV=Sdz. Based on these assumptions, we have the following Cl₂ gas mass balance equation for the gas bubbles [12]:

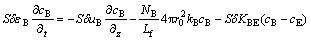        (9)

and for the emulsion phase

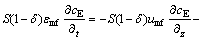
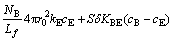           (10)

By applying the Laplace transformation technique, we have

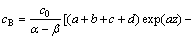
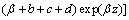                 (11)

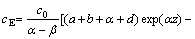
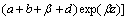                  (12)

where

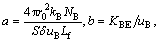
where c₀ is the concentration of Cl₂ gas at the bottom of the fluidized bed, and α and β are the parameters of the solutions of the following equation:

         (13)

From Eqs. (11) and (12), the concentrations of Cl₂ gas in both gas bubbles and emulsion phase at any given time can be calculated. By substituting the obtained values of c_B and c_E in Eq. (13), the consumption of Cl₂ gas in a time interval Δt is calculated. In gas bubbles, it is

          (14)

and in the emulsion phase, we have

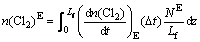            (15)

The consumption of Cl₂ gas in the whole fluidized bed is

                 (16)

The average concentration of Cl₂ gas in the height range of 0-L_f is calculated. In gas bubbles, it is

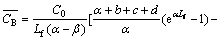
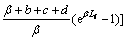                 (17)

and in the emulsion phase, it is

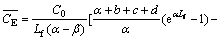
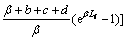                 (18)

It is necessary to estimate the parameters which appear in the above equations. They are estimated from the following empirical relationship and listed in Table1.

It is shown from the shrinking core model that the overall rate is determined by the inward diffusion of Cl₂ gas through the outer oxide shell at 1173-1273 K. The rate constant of interfacial reaction can be obtained from the experimental data based on Eq. (18). The calculated results of the kinetic parameters are listed in Table 2.

According to the Arrhenius equation, the apparent activation energy (E_a) can be calculated in the chlorination process. At 1173-1273 K, the apparent activation energy is 9.17 kJ/mol, showing that the reaction rate is mainly controlled by the diffusion control.

The chlorination of natural rutile particles in the gas bubbles is virtually negligible and the rising gas bubbles merely act as suppliers of chlorine gas to the emulsion phase under the experimental conditions employed in this work. Assuming the bubble phase has no solid particles, according to the above parameters, the a is approximately equal to zero. Bringing the parameters into the expression of b,c and d, the results are obtained as follows: b=538.3, c=11873.7, d = 9947.2.

Bringing the above parameters into formula (13), α and β can be obtained, and the initial concentration of C₀ can be calculated approximately according to the following equation:

PV=nRT                                   (19)

C₀=n/V=P/(RT)=11.7 mol/m³

As the solid particles in the bubble phase are little, we can approximately ignore the impact of the concentration of chlorine gas along the bed height distribution. Gas-solid reaction mainly occurs in the emulsion phase. Bringing the above parameters into formula (18) the average concentration of emulsion phase is obtained.

When the reaction conditions are as follows:  gaseous chlorine flow 0.036 m³/h, inlet gas pressure 0.14 MPa, the addition amount of carbon 30% of the rutile addition amount and the temperature 1173-1273 K, the average concentration of chlorine in the milk phase is 0.3 mol/m³.

The average concentration of emulsion phase in the range of fluidized bed is calculated as 0.3 mol/m³.

Based on the mathematical model, under the condition of vigorous bubbling, the decrease of Cl₂ concentration in gas bubbles is minor, which results in a significant difference in Cl₂ concentration between both phases. This is caused by the much higher upward flow rate of Cl₂ in the form of gas bubbles than gas mass transfer [18].

Table 1 Empirical relationship for calculating parameters and numerical values of parameters

Table 2 Kinetic parameters of boiling chlorination reaction

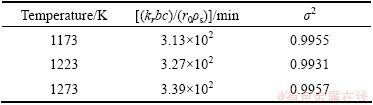
5 Conclusions

1) When using C as reductant, the thermodynamics analysis of different TiCl₄ partial pressure systems show that: TiO₂+2C+2Cl₂=TiCl₄+2CO dominates at high temperatures; Fe₂O₃-C chlorination system follows the same law.

2) With the increase of the generating CO ratio, η, the effect of temperature increases, while the Gibbs free energy at high reaction temperature is more negative; meanwhile, with the η increasing, the effect of the partial pressure of product TiCl₄ on Gibbs free energy decreases in this reaction.

3) Using the two-phase model for the fluidized bed, the interfacial reaction rate constant is determined by the experiment. At 1173-1273 K, the apparent activation energy is 9.17 kJ/mol, and the reaction rate is mainly controlled by the diffusion control.

4) The average concentration of emulsion phase in the range of fluidized bed is calculated as.0.3 mol/m³.

Nomenclature

C:

Cl₂ concentration;

C₀:

Initial concentration of Cl₂;

C_i:

Cl₂ concentration at the reaction interface;

C_s:

Cl₂ concentration at particle surface ;

d_s:

Particle diameter;

d_B:

Bubble diameter in fluidized bed;

D:

Diffusivity of Cl₂;

D_e:

Effective diffusivity of Cl₂ in rutile particle shell;

k:

Overall rate constant;

R:

Reaction rate;

k_g:

Gas film mass transfer coefficient;

k_r:

Rate constant of interfacial reaction;

K_BE:

Gas exchange coefficient between gas bubbles and emulsion phase;

K_BC:

Gas exchange coefficient between bubble halo and bubble phase;

K_CE:

Gas exchange coefficient between bubble halo and emulsion phase;

L_f:

Height of fluidized bed;

L_mf:

Height of fluidized bed at incipient fluidization;

M:

Mole mass;

n:

Mole number;

N_B:

Number of rutile particles in bubbles phase;

r_i:

Radius of reaction interface;

r₀:

Radius of particles;

S:

Cross sectional area of fluid bed;

t:

Time;

T:

Thermodynamic temperature;

u_B:

Rising velocity of gas bubbles;

u₀:

Superficial velocity of fluidizing gas;

u_mf:

Incipient fluidization velocity;

Re:

Reynolds number;

γ:

Volume fraction of fluidized particles in gas bubbles;

δ:

Volume fraction of gas bubbles in fluidized bed;

ε_mf:

Void fraction at incipient fluidization;

ρ_s:

Density of fluidized particles.

B:

Gas bubbles;

E:

Emulsion phase.

References

[1] ADIPURI A, ZHANG G Q, OSTROVSKI O. Chlorination of titanium oxycarbide produced by carbothermal reduction of rutile [J]. Metallurgical and Materials Transactions B, 2008, 39(1): 23-34.

[2] BARIN I, SCHULER W. On the kinetics of the chlorination of titanium dioxide in the presence of solid carbon [J]. Metallurgical and Materials Transactions B, 1980, 11(2): 199-207.

[3] YANG F, HLAVACEK V. Carbochlorination kinetics of titanium dioxide with carbon and carbon monoxide as reductant [J]. Metallurgical and Materials Transactions B, 1998, 29(6): 1297-1307.

[4] BERGHOLM A. Chlorination of rutile [J]. Transaction of American Institute of Mining, Metallurgical, and Petroleum Engineers, 1961, 221(121): 1121-1128.

[5] YOUN I J, PARK K Y. Modeling of fluidized bed chlorination of rutile [J]. Metallurgical and Materials Transactions B, 1989, 20(6): 959-966.

[6] ZHOU L, SOHN H Y. Mathematical modeling of fluidized-bed chlorination of rutile [J]. AIChE Journal, 1996, 42(11): 3102-3112.

[7] WANG Yu-ming, LIU Rui-feng, ZHOU Rong-hui, SHAO Bao-shun, WEI Qing-song, YUAN Zhang-fu, XU Chong. Thermodynamics on the reaction of carbochlorination of titania for getting titanium tetrachloride [J]. Computers and Applied Chemistry, 2006, 23(3): 263-266.

[8] YUAN Zhang-fu, ZHU Yuan-qing, XI Liang, XIONG Shao-feng, XU Bing-sheng. Experiment of TiCl₄ preparation with multistage series combined fluidized bed [J]. Transactions of Nonferrous Metals Society of China, 2013, 23(1): 283-288.

[9] XIONG Shao-feng, YUAN Zhang-fu, XU Cong, XI Liang. Composition of off-gas produced by a combined fluidizing chlorination of titanium slag [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(1): 128-134.

[10] DAVIDSON J F, HARRISON D. Fluidized particles [M]. Cambridge: Cambridge University Press, 1963: 19-20.

[11] KUNII D, LEVENSPIEL O. Bubbling bed model for flow of gas through a fluidized bed [J]. Industrial and Engineering Chemistry Fundamentals, 1968, 7(3): 446-452.

[12] FUKUNAKA Y, MONTA T, ASAKI Z, KONDO Y. Oxidation of zinc sulfide in a fluidized bed [J]. Metallurgical and Materials Transactions B, 1976, 7(3): 307-314.

[13] CHEN Gan-tang, LIANG Yu-heng. Technology foundation of chemical reaction [M]. Beijing: Science Press, 1978: 259, 309. (in Chinese)

[14] TOSHISADA M. Iron and steel metallurgy series: 1, Principles of iron making and steelmaking [M]. CHEN Xiang-wu. Beijing: Metallurgical Industry Press, 1980: 74-75. (in Chinese)

[15] KUNII D, LEVENSPIEL O. Bubbling bed model for kinetic processes in fluidized beds: Gas-solid mass and heat transfer and catalytic reactions [J]. Industrial and Engineering Chemistry, 1968, 7(4): 481-492.

[16] RICHARDSON J F, SZEKELY J. Mass transfer in a fluidised bed [J]. Transactions of the Institution of Chemical Engineers, 1961, 39(3): 212-225.

[17] KUNII D, LEVENSOPIEL O. Fluidization engineering [M]. China University of Petroleum. Beijing: China Petrochemical Press, 1977: 190-191. (in Chinese)

[18] FUKUNAKA Y, MONTA T, ASAKI Z, KONDO Y. Oxidation of zinc sulfide in a fluidized bed [J]. Metallurgical and Materials Transactions B, 1976, 7(3): 307-314.

肯尼亚天然金红石矿沸腾氯化热力学和动力学

牛丽萍^1,2，张廷安^1,2，倪培远^1,2，吕国志^1,2，欧阳全胜³

1. 东北大学 材料与冶金学院，沈阳 110819；

2. 东北大学 多金属共生矿生态利用教育部重点实验室，沈阳 110819；

3. 湖南有色金属研究院，长沙 410100

摘  要：以焦炭作还原剂，利用天然金红石和氯气制备四氯化钛。在1173到1273 K的温度范围内，对肯尼亚天然金红石颗粒在间歇式流化床中的氯化反应热力学和动力学进行研究。体系的热力学分析显示：生成CO的反应在高温下占主导地位；若生成CO反应的比率η越大，且随着体系反应受温度的影响加剧，高温下反应的吉布斯自由能越负；同时，η增大，产物中TiCl₄分压对反应的吉布斯自由能的影响趋于减小。应用气-固多相反应理论和流化床两相模型建立反应的数学模型，计算了气泡相和乳相中模型的各种参数，床层高度范围内氯气的平均浓度为0.3 mol/m³。结果表明：天然金红石氯化反应主要在乳相中进行，反应速率主要由界面反应控制。

关键词：天然金红石；热力学；动力学；气-固反应；流化床；两相模型

(Edited by Hua YANG)

Foundation item: Projects (51374064, 51004033, 51074044) supported by the National Natural Science Foundation of China; Project (2012AA062303) supported by High-tech Research and Development Program of China

Corresponding author: Li-ping NIU; Tel: +86-24-83686283; E-mail: niulp@smm.neu.edu.cn

DOI: 10.1016/S1003-6326(13)62887-3