参数振动和强迫振动激励下超长拉索的面内非线性振动
康厚军1,赵跃宇1,蒋丽忠2
(1. 湖南大学 土木工程学院,湖南 长沙,410082;
2. 中南大学 土木工程学院,湖南 长沙,410075)
摘要:针对大跨度斜拉桥中普遍存在的由桥面振动引起的斜拉索大幅振动问题,考虑由于索的初始垂度、大位移而引起的几何非线性因素的影响,推导索-梁组合结构的非线性运动方程,考虑索和梁的边界条件与连接条件,运用Galerkin方法对其进行离散,建立拉索在参数振动、强迫振动联合激励作用下的面内非线性振动方程。运用多尺度摄动方法,对由参、强联合激励作用下,斜拉索可能发生的大幅振动进行理论和数值分析。研究结果表明:桥面的低阶振动频率在小于拉索固有频率2倍附近时,容易引起大幅度的参强联合共振,而在大于拉索低阶频率2倍附近时,需要较大的激励幅值或初始挠动才能引起大幅度的参强联合共振。
关键词:索;斜拉桥;非线性系统;参数激励;强迫激励
中图分类号:O322 文献标志码:A 文章编号:1672-7207(2011)08-2439-07
In-plane nonlinear vibration of super long stay cables under parametric and forcied excitations
KANG Hou-jun1, ZHAO Yue-yu1, JIANG Li-zhong2
(1. College of Civil Engineering, Hunan University, Changsha 410082, China;
2. School of Civil Engineering, Central South University, Changsha 410075, China)
Abstract: Based on the large amplitude vibration problem of cable induced by oscillations of deck, the nonlinear equations of motion of cable-stayed beam composite structures were derived, in which the static sag and geometric nonlinearity of the cable were considered. Then, the in-plane nonlinear governing equations of cables under the parametric and forced excitations was established by means of treating of a simple connection condition and boundary condition of the cable-stayed beam composite structures and of a Galerkin's integral. Furthermore, the multi-scale perturbation method was applied to analyze the parametric and forced resonances of stay cables. The analytical and numerical results indicate that sufficiently low excitation amplitudes may stimulate large scale movements of the cables when the low-order natural frequencies of deck is close to and less than twice of natural frequency of cables, and it is worthy of note that the large amplitude vibration can be stimulated when the low-order natural frequencies of deck is close to and more than twice of frequency of cables and initial amplitudes of cables are biggish.
Key words: cables; cable-stayed bridge; nonlinear systems; parametric excitation; forced excitation
斜拉索自身的轻、柔及低阻尼的特点,在风雨或交通荷载的作用下,由于桥面或桥塔的振动,会引起拉索产生大幅度振动。近年来,在很多斜拉桥的现场观测中观测到了斜拉索在较小风速下产生大幅振动的现象,普遍认为是斜拉索产生参数共振的结果。因此,研究拉索的大幅振动具有非常重要的实际工程意义。Matsumoto等[1]研究了桥面的竖向振动引起的参数振动。亢战等[2]应用单个质量块分别模拟连续系统的拉索和梁,并将拉索振动问题简化为一个二自由度的非线性振动系统,对其参数振进行了研究。Gattulli等[3-4]研究了索-梁组合结构中索和梁的非线性内共振。汪至刚等[5]提出了索-梁组合结构的弦-质量块模型。陈水生和孙炳楠[6]对索-梁组合结构的弦-质量块模型进行了改进。赵跃宇等[7]建立了索-梁组合结构的运动控制方程,分析了其可能存在的内共振情形,赵跃宇 等[8-9]中分别研究了索-梁、索-拱组合结构中拉索的1/2亚谐波共振。以上研究基本上都是单独对拉索的强迫振动或参数振动进行研究,而工程实际中拉索应该是参数振动和强迫振动共同作用(简称参、强联合激励),关于这方面的研究甚少见到。本文作者针对这种情况,基于Hamilton原理,建立了索-梁组合结构的动力学微分方程。考虑索与梁的边界条件和连接条件得到拉索在参、强联合激励下面内非线性运动方程。利用Galerkin方法对其进行离散,应用多尺度法进行摄动分析,得到拉索在参、强联合激励下的稳态非平凡解,应用李雅普诺夫一次近似稳定判据对其稳定性进行分析,并用直接数值积分方法与近似解进行对比。
1 索-梁组合结构运动方程
桥塔和桥面在动荷载作用下的振动,使斜拉桥在施工阶段与成桥后的动力学成为非保守系统动力学问题。将斜拉桥施工阶段与成桥后的结构简化为图1所示的索-梁模型。该模型考虑桥面振动对索的影响,忽略塔对索动力学特性的影响。索的运动用直角坐标系Oxy描述,忽略梁的轴向变形影响,用坐标系Ow描述梁在竖直面内的运动。图1(a)中:f为拉索跨中初始垂度;l为索跨长;lb为梁长。梁的一端固定,索的一端铰接,另一端与梁耦合。图1(b)所示为索-梁的耦合振动模型。对索与梁作如下基本假设:不考虑索和梁的材料非线性;索在重力作用下垂度曲线近似为抛物线,忽略索的抗扭刚度、抗弯刚度及抗剪刚度。
利用Hamilton原理可以得到的索-梁组合结构运动微分方程[10]:
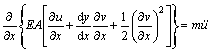 (1a)
(1a)
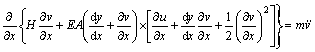
 (1b)
(1b)
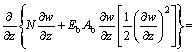
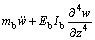 (1c)
(1c)
由图1(b)可得索与梁的边界条件和连接条件为:
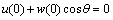 (2a)
(2a)
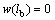 ,
,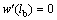 ,
,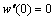 (2b)
(2b)
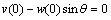 ,
,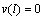 (2c)
(2c)
式中:y为拉索的静态变形曲线;Eb和E分别为梁和索的弹性模量;Ab和A分别为梁和索的截面面积;mb和m分别为梁和索的单位长度质量;N为梁所受的轴向力;H为拉索的静态轴向拉力;w和v分别为梁和索的横向振动位移;u为拉索长度方向的纵向位移。
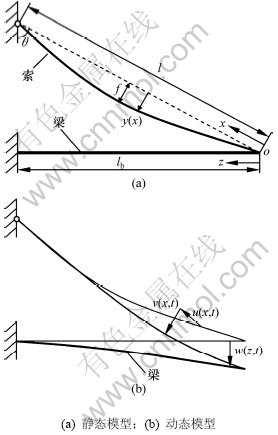
图1 索-梁组合结构模型
Fig. 1 Cable-stayed beam structure configurations
因为弹性拉索纵向变形远小于其横向变形,且在只考虑拉索的低阶横向振动模态时,横向振动模态和纵向振动模态不存在相互作用[11],因此,忽略拉索的纵向惯性力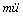 。由式(2a)可将式(1a)写为:
。由式(2a)可将式(1a)写为:
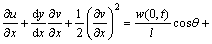
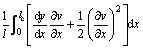 (3)
(3)
由于桥面的质量远大于索的质量,故这里忽略拉索振动对桥面梁振动的影响,将拉索的作用看成是对梁的一个弹性支撑[8-9],这样就可以把梁的边界条件简化为一端固支,一端受一个刚度为K的弹簧支撑,其中K=EAcos2θ/l。于是,梁的边界条件可以表示为:
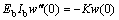 (4)
(4)
考虑式(2b),可将梁的竖向振动挠曲线设为:
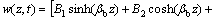
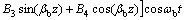 (5)
(5)
其中:Bn(i=1,2,3,4)为常系数,由边界条件(2b)确定;βb为ωb的函数;ωb为桥面梁的振动频率;详见文献[12]。ωb与K的关系可由梁的边界条件式(2b)和(4)确定。将z=0代入上式得:
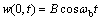 ,
,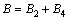 (6)
(6)
其中:B为桥面梁对拉索激励幅值。
再考虑索-梁结构的边界条件与连接条件(2c),可将索的一阶振动模态取为:
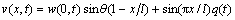 (7)
(7)
至此,分别将式(3),(6)和(7)代入式(1b),进行Galerkin积分,可得到拉索的面内横向振动的运动微分方程(引入黏性阻尼ζ):
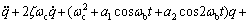
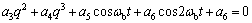 (8)
(8)
其中:
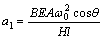 ;
;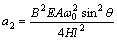 ;
;
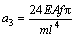 ;
;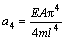 ;
;
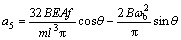 ;
;
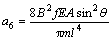 ;
;
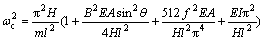 。
。
ωc为考虑拉索的倾角、垂度及桥面激励幅值影响的拉索频率。式(8)即为索-梁模型中拉索在参、强联合激励作用下的非线性振动方程。由于桥面对索的激励为竖向激励,故同时存在对斜拉索的轴向和横向激励,轴向激励表现为参数振动,在方程中体现在a1和a2 2项,而横向激励表现为强迫振动,体现在a5和a6两项。可以看出式(8)中参数振动项包含了斜拉桥桥面振动频率ωb及2ωb对拉索的激励,强迫振动项中也含有这2种频率的激励。另外,由拉索的非线性振动方程可看出:拉索的线性频率不但与索的垂度有关,而且与桥面的激励幅值也有关,这是索处于非保守系统的原因。
2 摄动力分析
引入无量纲小参数ε,设: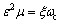 ,
,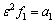 ,
,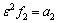 ,
,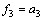 ,
,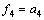 ,
,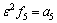 ,
,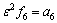 。将之代入式(8)中,则有:
。将之代入式(8)中,则有:
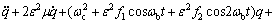
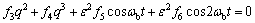 (9)
(9)
应用多尺度法对方程式(9)进行摄动分析,设解的形式为:
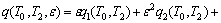
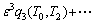 (10)
(10)
其中: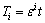 (i=0,2)。引入Dn=?/?Tn。将式(10)代入式(9),并按ε幂次整理得:
(i=0,2)。引入Dn=?/?Tn。将式(10)代入式(9),并按ε幂次整理得:
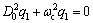 (11a)
(11a)
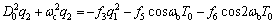 (11b)
(11b)
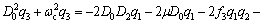
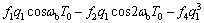 (11c)
(11c)
设式(11a)的解的复数形式为:
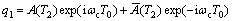 (12)
(12)
代入式(11b)可解得:
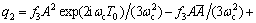
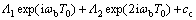 (13)
(13)
其中: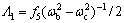 ;
;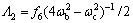 。
。
式中:cc为左边各项的共轭复数。
将式(12)与上式同时代入式(11c)得:
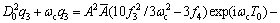
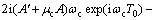
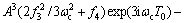
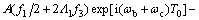
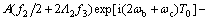
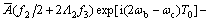
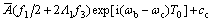 (14)
(14)
从式(14)可看出:当ωb≈2ωc和ωb≈ωc时,系统存在参数共振与强迫共振同时发生的现象。在本文分析中,讨论当ωb≈2ωc时系统在参数振动和强迫振动共同作用情况下的动力学特性。
设ωb=2ωc+ε2σ,σ为调谐参数,代入式(14)中消除久期项。设A=[aexp(iβ)]/2,a与β均为时间T2的函数,令γ=σT2-2β,分离实部与虚部,得到a与γ的一阶常微分方程组:
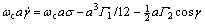 (15a)
(15a)
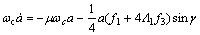 (15b)
(15b)
其中: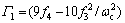 ;
;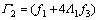 。令
。令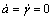 ,得到a和γ的稳态解as与γs。平凡解as=0,非平凡解可从以下幅频响应曲线方程中求出。
,得到a和γ的稳态解as与γs。平凡解as=0,非平凡解可从以下幅频响应曲线方程中求出。
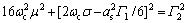 (16)
(16)
由式(16)可得到非平凡解as的表达式:
(1) 当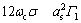 和
和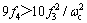 时, 有:
时, 有:
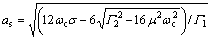 (17a)
(17a)
(2) 当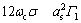 和
和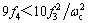 时, 有:
时, 有:
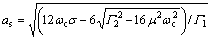 (17b)
(17b)
(3) 当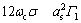 和
和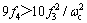 时, 有:
时, 有:
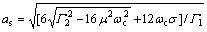 (17c)
(17c)
式(17)给出了稳态响应非平凡解的幅值。幅值的稳定性可通过式(15)对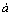 和
和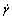 进行摄动,得到线性系统的特征值,根据李雅普诺夫一次近似稳定判据进行判断。稳态非平凡解稳定的充分条件为:
进行摄动,得到线性系统的特征值,根据李雅普诺夫一次近似稳定判据进行判断。稳态非平凡解稳定的充分条件为:
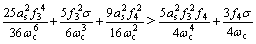 (18)
(18)
满足此条件的稳态解是稳定的,否则为不稳定。
3 算例分析
以目前某大桥中最长拉索为例进行相关分析。拉索主要参数为:mc=102.82 kg/m,l=577 m,A=0.124×10-2 m2,θ=35°,E=1.95×1011 N/m2,H=8 700 kN。当ωb≈2ωc,改变桥面的振幅也就是改变激励幅值B和激励频率ωb,得到了不同激励幅值和激励频率下的拉索跨中幅频曲线、幅幅曲线和时间历程。引入阻尼系数研究阻尼对拉索振动的影响。另外,将近似方法分析结果与数值积分结果进行了对比。
图2给出了在不同阻尼比ζ和不同激励频率情况下斜拉索跨中振动幅值与桥面(梁)激励幅值的关系。从图2(a)可知:当在阻尼比不变的情况下,拉索的激励频率为拉索频率的2倍即3.22(圆频率)时,一个激励幅值B对应的拉索响应有一个稳定非平凡解,只要桥面有轻微的振动,激励幅值要求不大,拉索即会发生大幅振动;当拉索激励频率小于拉索频率的2倍时,也只有一稳定非平凡解,并且要激起拉索的大幅振动,对激励幅值B的要求越来越大;当拉索的激励频率大于拉索频率的2倍时,在一定范围内,一个激励频率和一个激励幅值对应拉索响应有2个稳态非平凡解,大值为稳定解,小值为不稳定解,而只要有较小的激励幅值B在一定的初值条件下,拉索即可发生大幅振动。对于相同的激励幅值,频率越大,斜拉索的响应幅值也越大。另外,在大于拉索2倍频率的激励下,拉索的稳定解也表现出不同的特性。从图2可以看出:在频率3.292 Hz的激励下,响应幅值AE段对应一段激励幅值,拉索的激励幅值越大,拉索的稳定响应就越大,但在AE段,对拉索的初始挠动条件要求较高,初始挠动必须达到斜拉索所对应稳定响应值,在相应的激励幅值下才能激起相应的稳定响应。而在A点以上部分,只要达到相应的激励幅值,有即使初始挠动为0,也能引起大幅振动。图2(b)所示为提高斜拉索阻尼比后,拉索的激励幅值、激励频率与拉索跨中响应的关系。对比图2(a),将阻尼比从0.000 1提高到0.006 0,提高了拉索发生大幅振动所需的激励幅值,但对响应幅值的抑制作用甚微。此外,对比近似方法与数值积分方法的结果,两者吻合良好,采用近似方法可对拉索的非稳定情况进行分析。
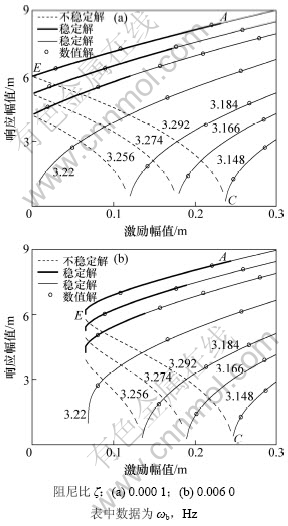
图2 激励幅值和拉索响应幅值关系
Fig.2 Relationship between excitation amplitude and amplitude of cable
图3给出了斜拉索在不同阻尼比情况下不同拉索激励幅值对应的幅频响应曲线。从图3(a)可以看出:在相同阻尼比的情况下,不同激励幅值对应于不同的响应;当激励幅值越小时,如B=0.01 m,拉索响应存在2个非常靠近的稳态非平凡解,大值为稳定解,小值为不稳定解。随着拉索激励幅值的增大,拉索响应的两个稳态非平凡解相差越来越大,仍然大值为稳定解,小值为不稳定解。另外,对于稳定解,也表现出不同特性。当激励幅值B=0.25 m时,稳定响应AE段所对应的激励频率约为3.15~3.29 Hz,在此范围之间,即使拉索的初始挠动为0,在该情况下也能激起大幅振动。而当激励频率继续增加,即大于3.29时,要使拉索产生更大幅度的振动初始挠动条件要求较高,需达到相应稳定响应值才能激起大幅振动。对比图3(a)和(b)可以看出:提高斜拉索的阻尼,对拉索的响应影响非常有限,仅提高了引起拉索大幅振动的激励幅值B。
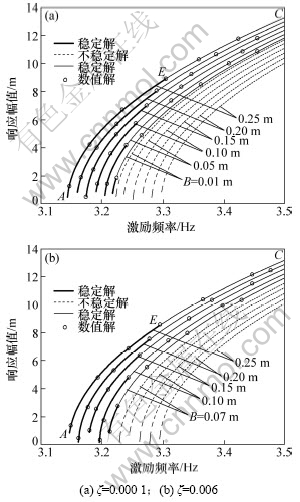
图3 幅频响应曲线
Fig.3 Frequency response curves
图4所示为斜拉索在不同阻尼比时,跨中响应的时间历程。该图表示出了响应的稳定过程,当经过一定时间后斜拉索的振动趋于稳定。从图4可以看出:增加斜拉索的阻尼,对拉索的稳定振动的振幅几乎没有影响,而只是减少了稳定振动所需的时间。这与文献[9]所得结论相反,原因为文献[9]中拉索较短,与文献[13]所得结果一致。通过比较分析可知:阻尼比对短索的振动较为敏感,而对长索影响较小;另外,从图中可见,斜拉索的稳定振动幅值达到7.15 m,增加阻尼比后仍有6.88 m,应引起足够的重视。
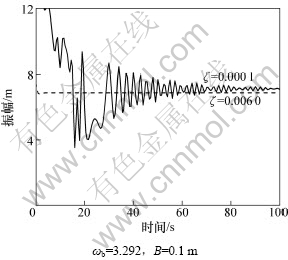
图4 不同阻尼时拉索的时间历程
Fig.4 Time history of cable with different damping
图5所示为斜拉索在同一激励幅值情况下不同激励频率激起大幅振动所需的不同初始条件和系统最后达到稳定状态的振动幅值。从图5可知:当激励频率从3.256 Hz提高到3.292 Hz时,虽然系统的稳定振幅从5.43 m增加到了6.88 m,但斜拉索的最低初始挠度从4.6 m提高到了7.5 m。由此说明:给定系统的激励频率越大,在激励幅值不变时,斜拉索在初始挠度不大时,不易引起大幅振动。
图6给出了系统在同样的阻尼比条件下以相同激励频率和激励幅值对斜拉索进行激励时,拉索的时间历程。从图6可知:拉索初始挠度不同时系统振动达到稳定的时间不同,初值越大,达到稳定所需的时间越短,而对最终稳定振动的幅值没有影响。
图7给出了系统阻尼不变时同一激励频率不同激励幅值时拉索跨中的时间历程。从图7可知:在激励频率为ωb=3.292 Hz时,以B=0.25 m的激励幅值对系统进行激励,所需的初始挠度为0.01 m,共振幅值达到8.49 m;而以B=0.07 m激励时,所需初始挠度大于10 m共振幅值为6.33 m。由此说明:对系统进行激励,在同一激励频率激励下,不同的激励幅值引起不同的共振幅值;激励幅值越大,共振幅值越大,所需的初始挠度越小。
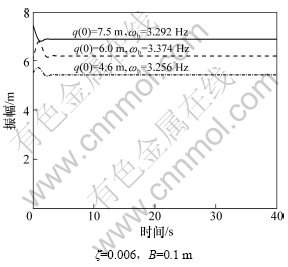
图5 不同激励频率时拉索的时间历程
Fig.5 Time history of cable with different excitation frequencies
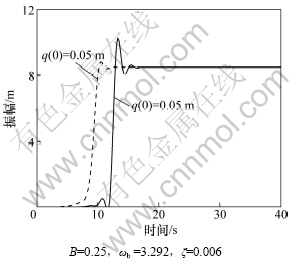
图6 不同初时条件时拉索的时间历程
Fig.6 Time history of cable with different initial deflections
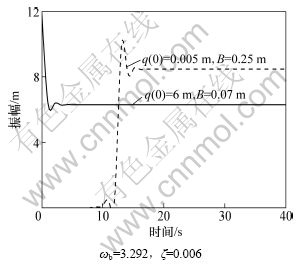
图7 不同激励幅值拉索的时间历程
Fig.7 Time history of cable with different excitation forces
4 结论
(1) 在斜拉桥系统中,当桥面或桥塔的某一低阶局部自振频率在拉索的自振频率的2倍左右的较小范围内时,斜拉索将发生严重的参数振动与强迫振动,从而使拉索具有过大的振幅,影响桥梁的安全性与耐久性。
(2) 激励幅值越大,拉索容易产生大幅参强共振的区间越大。这个区间指对拉索初始挠度不作要求的区间,只有在这个区间才容易产生大幅振动。
(3) 外激励频率在大于2倍索频率附近时,虽然只要有较小的激励幅值便可能引起更大幅度的参强共振,但需要较大的拉索初始挠度;而激励频率在小于2倍索频率附近时,虽然需要较大一点的激励幅值,但对初始挠动的要求不高。因此,激励频率在小于2倍索频率附近时,更易发生大幅的参、强共振。
(4) 当发生参、强联合共振时,增大阻尼对超长拉索并不能有效减小振动幅值,对短索有一定的抑制作用。因此,要对超长拉索的振动进行控制必须对桥塔和桥面的振动幅度进行控制。
(5) 拉索的初始条件对拉索产生大幅参强共振非常关键,当其他条件不变时,初始挠度越大,则越易产生大幅振动,系统振动也更快达到稳定状态。
参考文献:
[1] Matsumoto M, Shiraishi N, Shirato H. Rain-wind induced vibration of cables of cable-stayed bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 43(1/3): 2011-2022.
[2] 亢战, 钟万勰. 斜拉桥参数共振问题的数值研究[J]. 土木工程学报, 1998, 31(8): 14-22.
KANG Zhan, ZHONG Wan-xie. Numerical study on parametric resonance of cable in cable stayed bridge[J]. China Civil Engineering Journal, 1998, 31(8): 14-22.
[3] Gattulli V, Lepidi M. Nonlinear interactions in the planar dynamics of cable-stayed beam[J]. International Journal of Solids and Structures, 2003, 40(18): 4729-4748.
[4] Gattulli V, Martinelli L, Perotti F, et al. Nonlinear oscillations of cables under harmonic loading using analytical and finite element models[J]. Computer Methods in Applied Mechanics And Engineering, 2004, 193(1/2): 69-85.
[5] 汪至刚, 孙炳楠. 斜拉桥参数振动引起的拉索大幅振动[J]. 工程力学, 2001, 18(1): 103-109.
WANG Zhi-gang; SUN Bing-nan. Cable vibration for cable stayed bridge by parametric response[J]. Engineering Mechanics, 2001, 18(1): 103-109.
[6] 陈水生, 孙炳楠. 斜拉桥索-桥耦合非线性参数振动数值研究[J]. 土木工程学报, 2003, 36(4): 70-75.
CHEN Shui-sheng, SUN Bing-nan. Numerical study on nonlinear parametric vibrationof coupled cables and bridge decks[J]. China Civil Engineering Journal, 2003, 36(4): 70-75.
[7] 赵跃宇, 蒋丽忠, 王连华, 等. 索-梁组合结构的动力学建模理论及其内共振分析[J]. 土木工程学报, 2004, 37(3): 69-73.
ZHAO Yue-yu, JIANG Li-zhong, WANG Lian-hua, et al. The dynamical modeling theory and internal resonance of cable beam composite structure[J]. China Civil Engineering Journal, 2004, 37(3): 69-73.
[8] 赵跃宇, 杨相展, 刘伟长, 等. 索-梁组合结构中拉索的非线性响应[J]. 工程力学, 2006, 23(11): 153-158.
ZHAO Yue-yu, YANG Xiang-zhan, LIU Wei-chang, et al. Non-linear response of cables in cable-stayed beam structure[J]. Engineering Mechanics, 2006, 23(11): 153-158.
[9] 赵跃宇, 吕建根. 索-拱组合结构中斜拉索的非线性参数振动[J]. 土木工程学报. 2006, 39(12): 67-72.
ZHAO Yue-yu, L? Jiang-gen. Non-linear parametric vibration of cables in cable-arch composite structures[J]. China Civil Engineering Journal, 2006, 39(12): 67-72.
[10] Gattulli V, Morandini M, Paolone A. Parametric analytical model for non-linear dynamics in cable-stayed beam[J]. Earthquake Engineering and Structural Dynamic, 2002, 31: 1281-1300.
[11] 赵跃宇, 王连华, 陈得良, 等. 斜拉索面内振动和面外摆动的耦合分析[J]. 土木工程学报, 2003, 36(4): 65-69.
ZHAO Yue-yu, WANG Lian-hua, CHEN De-liang, et al. Coupled analysis of out of plane oscillation and in plane vibration for stay cable[J]. China Civil Engineering Journal, 2003, 36(4): 65-69.
[12] Wang T M, Nettleton R H, Keita B. Natural frequencies for out-of-plane vibrations of continuous curved beams[J]. Journal of Sound and Vibration, 1980, 68(3): 427-436.
[13] 杨素哲, 陈艾荣. 超长斜拉索的参数振动[J]. 同济大学学报: 自然科学版, 2005, 33(10): 1303-1308.
YANG Su-zhe, CHEN Ai-rong. Parametric oscillation of super long stay cables[J]. Journal of Tongji University: Natural Science, 2005, 33(10): 1303-1308.
(编辑 陈爱华)
收稿日期:2010-10-20;修回日期:2010-12-25
基金项目:国家自然科学基金重点资助项目(11032004);湖南省博士后计划外项目(897205006)
通信作者:康厚军(1977-),男,四川安岳人,讲师,博士,从事结构动力学研究;电话:0731-88822722;E-mail:kang.echo@gmail.com