考虑负荷动态模型的船舶电力系统暂态电压稳定分析
王新枝,夏立,张超
(海军工程大学 电气工程学院,湖北 武汉,430033)
摘要:为了研究型船舶独立电力系统的电压稳定问题,将基于稳定域边界二次逼近的暂态电压分析方法应用到新型船舶独立电力系统的暂态电压稳定分析。通过建立系统暂态分析的数学模型,利用牛顿法求取故障后系统主导不稳定平衡点(CUEP),采用基于稳定域二次逼近的稳定判据,进行系统暂态电压稳定分析。同时,考虑不同故障位置对于求解CUEP过程中电动机和直流系统控制器状态量计算的影响。通过简化的新型独立电力系统模型对上述方法进行验证。研究结果表明:该分析方法能够获得暂态电压稳定裕度指标,准确判断该独立电力系统的暂态电压稳定状态。
关键词:独立电力系统;暂态电压稳定;稳定裕度;二阶逼近
中图分类号:TM712 文献标志码:A 文章编号:1672-7207(2014)07-2231-06
Transient voltage stability analysis for ship power system considering load dynamic model
WANG Xinzhi, XIA Li, ZHANG Chao
(College of Electric Engineering, Naval University of Engineering, Wuhan 430033, China)
Abstract: In order to study the voltage stability of new ship isolated power system (IPS), transient voltage stability analysis method based on second-order approximation of stability boundary was applied to transient voltage stability analysis for the new isolated power system. The method modeled power system acquired controlling unstable equilibrium point (CUEP) after fault was removed by Newton iteration method. The transient voltage stability analysis could be realized by transient voltage stability criterion based on second-order approximation of stability boundary. The influence of different fault position to quantity of state calculation of motor and DC system controller was also considered. Using simplified new IPS, the correctness of the method was validated. The results show that the method can obtain transient voltage stability allowance and estimate IPS transient voltage stability state.
Key words: isolated power system; transient voltage stability; stability margin; second-order approximation
全电力船舶是未来船舶的发展趋势,其独立电力系统IPS(isolated power system)采用集成化技术进行电能的生产、输送、变换和分配,担负船舶绝大部分系统的能源供应,如推进系统、通信系统、导航系统等等。能在较复杂的环境下维持电力系统的运行,并进行合理的自动控制[1-3]。IPS有如下显著特点:(1) 电动机负载多;(2) 单个负载容量可与单台发电机容量相比拟,特别是新型的IPS,其推进系统容量占整个电力系统容量的75%以上;(3) 馈电线路短,电气距离近。因此,其暂态电压问题尤为突出[4]。同时,接近恒功率特性电源的广泛使用,系统更易于发生电压失稳,其研究受到越来越多的重视[5-7]。针对电力系统的暂态电压稳定分析,文献[4]建立了传统独立电力系统的分析模型,通过计算稳定裕度并与仿真比较,求取了暂态电压稳定临界切除时间。文献[8]提出了基于稳定域边界二阶逼近的暂态电压稳定判据,并在单机单负荷系统上进行了仿真验证。新型IPS的发电模块采用整流发电机组,输配电模块采用直流母线和直流区域配电等特点,弱化了各个发电机之间的暂态功角稳定问题,也给暂态电压稳定分析带来新的挑战。目前,没有针对新型IPS的暂态电压稳定分析。为此,本文作者建立新型IPS暂态分析的数学模型,采用电力系统暂态电压稳定快速判断方法[9],对系统指定位置故障进行暂态电压稳定分析。
1 系统模型
新型IPS的简化系统结构如图1所示。图1中电站由同步发电机带整流器组成,采用中压直流配电网络。DC-ZEDS为直流区域配电系统,为常规负载供电。推进电机M1和M2由变频器供电。

图1 IPS系统结构
Fig. 1 Configuration of IPS reference system
1.1 发电机数学模型
采用计及励磁系统动态的三阶发电机模型[10],忽略定子d绕组、q绕组暂态,并忽略阻尼绕组作用。
 (1)
(1)
式中: 为第i台同步电机转子角(相对于同步旋转参考轴的角位置);
为第i台同步电机转子角(相对于同步旋转参考轴的角位置); 为第i台同步电机角速度,
为第i台同步电机角速度, 为参考发电机角速度;
为参考发电机角速度;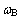 为基准频率;
为基准频率;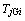 为第i台同步电机惯性时间常数,定义为转动惯量的标幺值乘以时间基值;
为第i台同步电机惯性时间常数,定义为转动惯量的标幺值乘以时间基值;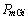 为第i台同步电机机械功率;
为第i台同步电机机械功率; 为阻尼系数;
为阻尼系数; 为d轴暂态开路时间常数;
为d轴暂态开路时间常数;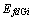 为励磁电压。
为励磁电压。
电磁功率 可表示为
可表示为
 (2)
(2)
式中: 为发电机d轴暂态电抗;
为发电机d轴暂态电抗; 为第i台同步电机虚拟电势;
为第i台同步电机虚拟电势; 为第i台同步电机输出电压;
为第i台同步电机输出电压; 为第i台同步电机相角;
为第i台同步电机相角; 和
和 分别为
分别为 的实部和虚部分量。
的实部和虚部分量。
在含感应电动机的电力系统模型中,为了得到模型的双曲平衡点进而判断系统的暂态稳定,典型做法是以1台发电机作为无穷大平衡节点。但独立电力系统的发电机惯量较小,不能用无穷大母线近似[4],因此式(1)中加入了参考发电机的角速度。
1.2 励磁系统和感应电动机数学模型
采用文献[11]中的经典励磁系统模型。基本方程见式(3)。感应电动机负荷模型采用三阶模型,见式(4)。
 (3)
(3)
 (4)
(4)
式中: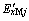 和
和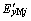 分别为第j台电动机定子暂态电势
分别为第j台电动机定子暂态电势 在同步坐标x轴和y轴上的投影;
在同步坐标x轴和y轴上的投影; 为定子开路暂态时间常数;
为定子开路暂态时间常数; 为转子惯性时间常数;
为转子惯性时间常数;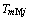 为电动机负载力矩。电动机滑差
为电动机负载力矩。电动机滑差 。
。
1.3 网络模型
直流系统的数学模型采用准稳态模型[12]:
 (5)
(5)
其中: 和
和 分别为第i台发电机整流输出直流电压和电流;
分别为第i台发电机整流输出直流电压和电流; 和
和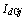 分别为第i台电动机直流侧的母线电压和输入电流;
分别为第i台电动机直流侧的母线电压和输入电流; 为整流控制角;
为整流控制角; 为逆变控制角。P和Q分别为相应的有功和无功功率。
为逆变控制角。P和Q分别为相应的有功和无功功率。
新型IPS采用多相整流发电机,可以采用多相交流发电机带不控整流方式模拟。因此只在逆变侧列写直流控制方程,采用文献[13]的定电压控制模式:
 (6)
(6)
网络方程为 。由于变流器的存在,在计算网络导纳矩阵时,无法将发电机的暂态电抗和负荷电动机的暂态阻抗和静态恒导纳一并计入,只需要计算直流输电网络的导纳。通过直流系统的准稳态模型将发电机和负荷的输入输出电压、电流等效至直流系统进行计算。
。由于变流器的存在,在计算网络导纳矩阵时,无法将发电机的暂态电抗和负荷电动机的暂态阻抗和静态恒导纳一并计入,只需要计算直流输电网络的导纳。通过直流系统的准稳态模型将发电机和负荷的输入输出电压、电流等效至直流系统进行计算。
2 独立电力系统暂态电压稳定快速判断的原理和方法
2.1 暂态电压稳定快速判断的原理
在暂态电压稳定研究方面,时域仿真法计算耗时,无法标量稳定裕度;能量函数法仅可用于存在能量函数的电力系统稳态模型,同时无法提供故障后状态变量的时间响应[4]。非线性动力学方法为电力系统的暂态稳定分析提供了快速有效的判断方法[14]。采用稳定域边界多项式近似方法,避免构造系统能量函数,降低了对系统模型的要求,同时可充分考虑负荷特性,有较好的可行性。根据稳定域的概念,电力系统的暂态电压稳定性由故障切除之后的系统初始状态和故障后系统暂态电压稳定域边界的相对距离来确定。由此,通过构建暂态电压稳定裕度指标,根据故障清除时刻的系统状态,即可判断系统能否保持电压稳定,从而不必对扰动清除后的系统进行仿真,提高了效率,同时能够确定故障的临界切除时间。
而故障后的系统暂态电压稳定域,即系统故障后的稳定平衡点(SEP)吸引域,其边界由稳定边界上不平衡稳定点的稳定流形的并集构成。主导不平衡稳定点(CUEP)是其稳定流形首先与系统持续故障轨线相交的不平衡稳定点[9]。对于给定位置的系统故障,系统暂态电压稳定域可以通过计算CUEP处的稳定流形 实现。
2.2暂态电压稳定快速判断的步骤
(1) 独立电力系统动态过程的模型描述。独立电力系统暂态电压稳定的动态过程采用下述微分代数方程(DAE)描述:
 (7)
(7)
式(7)中,微分方程描述系统各个元件的动态,包括发电机状态、电动机状态和变流器(主要是逆变器)状态,采用前述的发电机、电动机模型和变流器模型。代数方程为系统各个节点的功率平衡方程。发电机和电动机节点的功率平衡方程如下:
 (8)
(8)
其中: 为
为 的相角;
的相角; 为第j台电动机定转子互感抗;
为第j台电动机定转子互感抗;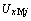 和
和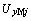 分别为第j台电动机电压
分别为第j台电动机电压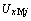 的x轴和y轴分量;KZ为负荷节点的阻抗折算比;
的x轴和y轴分量;KZ为负荷节点的阻抗折算比;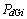 ,
, 和
和 分别为发电机节点和负荷节点功率,
分别为发电机节点和负荷节点功率,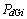 的表达式如下。
的表达式如下。
 (9)
(9)
根据式(8)的稳态方程进行初值计算,包括发电机状态变量初值、负荷(电动机)状态变量初值和相应的导出参数。考虑到新型独立系统的特殊性,在负荷(电动机)节点处电压相角初值可设置为0°。同时发电机之间无交流联接,弱化了相互之间的功角影响。因此,不同容量的发电机之间的功角变化不能说明系统发生功角失稳。
(2) 求解系统故障后的主导不平衡稳定点(CUEP)。首先根据文献[4]中的方法,采用潮流断面的模态分析法确定主导电动机母线。将式(8)的稳态方程线性化,观察电压和无功功率之间的关系。由系统简化电压模式的Jacobian矩阵,计算各个模态下的无功功率增量变化,进而得出节点的电压无功灵敏度及相应的模态参与因子。通过分析比较电动机母线参与因子,较大的即为该故障下主导电动机母线。
然后,对主导电动机母线以外的部分由故障后稳定平衡点的状态进行戴维南等值,见图2。为了便于分析,图2中已将变流器等效为受控源。
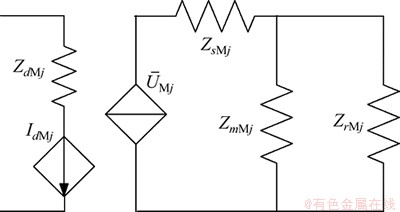
图2 主导负荷母线处的等值电路
Fig. 2 Equivalent circuit of system at controlling load bus
进而对负荷中感应电动机部分采用其稳态等值电路,可得感应电动机的转矩平衡方程如下:
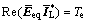 (10)
(10)
式中:等值电势 和等值电流
和等值电流 均为相应节点处直流母线转化至交流侧的向量。该方程中较大的根对应CUEP附近的滑差。在等值电路以外的系统均采用故障后的稳定平衡点,以此为初值经牛顿迭代确定CUEP处各个参数值。
均为相应节点处直流母线转化至交流侧的向量。该方程中较大的根对应CUEP附近的滑差。在等值电路以外的系统均采用故障后的稳定平衡点,以此为初值经牛顿迭代确定CUEP处各个参数值。
需要注意的是:考虑到变流器的定电压调节作用,在确定主导电动机母线后,应根据故障点位置,进行合适的电路等值。若故障点发生在相应电动机的交流母线部分,则可通过直流系统等效模型,直接将直流侧变量值转化为交流侧变量值。此时,迭代初值中xMj应选择故障后的SEP处的值;若故障点位置在直流母线部分,在计算CUEP过程中,必须考虑变流器控制作用,将控制方程代入式(10),通过牛顿迭代,确定相应变量的值。此时,迭代初值中xMj应选择上述CUEP附近的值。
(3) 计算暂态电压稳定裕度指标。对于独立电力系统暂态分析的微分代数方程(式(7))所表示的非线性系统,其1型不平衡稳定点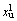 的稳定子流形描述为[4, 15-16]
的稳定子流形描述为[4, 15-16]
 (11)
(11)
其中: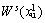 为1型不平衡稳定点
为1型不平衡稳定点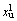 的稳定子流形;
的稳定子流形; 为Jacobian矩阵
为Jacobian矩阵 的不稳定特征值。由此,暂态电压稳定裕度指标为[4]
的不稳定特征值。由此,暂态电压稳定裕度指标为[4]
 (12)
(12)
其中: 为故障后系统初始状态;
为故障后系统初始状态; 为稳定域边界
为稳定域边界
的二阶逼近。一次项系数 为Jacobian矩阵不稳定特征值
为Jacobian矩阵不稳定特征值 所对应的左特征向量。矩阵Q满足Lyapunov矩阵方程
所对应的左特征向量。矩阵Q满足Lyapunov矩阵方程 。
。
当I(x(tF))>0时,故障后系统的初始状态x(tF)在故障后稳定域内部,系统暂态电压稳定,反之则不稳定。当I(x(tF))=0,x(tF)处于稳定域边界上,系统暂态电压临界稳定。
3 算例分析
由于独立电力系统馈电线路短,电气距离近,可将多台发电机用1台等效发电机替代。因此,本算例考虑单台发电机,单台电动机负荷情况,见图3。发电机、励磁系统以及电动机参数分别见表1和表2(其中各参数均已转化为标幺值形式)。
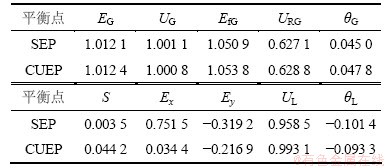
故障为电动机侧交流母线短路接地,经一段时间后故障消除。故障消除前后系统结构保持不变。故障后系统稳定平衡点SEP和不稳定平衡点CUEP如表3所示。CUEP处Jacobian矩阵特征值只有1个有正实部,满足文献[4]中关于1型不平衡稳定点的要求。则参数矩阵见式(13)和(14)。代入稳定域二次逼近表达式,得出系统暂态电压稳定的裕度指标见式(15)。
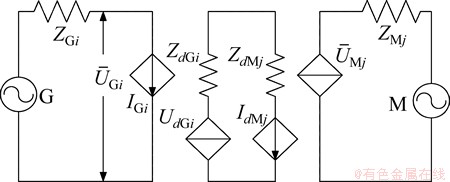
图3 系统结构
Fig. 3 System structure
表1 发电机及励磁系统参数
Table 1 Parameters of generator and field system

表2 电动机参数
Table 2 Parameters of motor

表3 故障后的平衡点
Table 3 Post fault equilibrium point

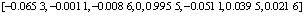 (13)
(13)
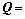
 (14)
(14)

 (15)
(15)
该指标为0时对应的故障切除时间,即为电力系统暂态电压的临界切除时间。此处时间为10.068 s。
在PSCAD中建立该独立电力系统的仿真模型,时域仿真结果为10.07 s。当故障切除时间为10.069 s和10.07 s时,电动机滑差和电压的时域仿真结果见图4~7。在图6和图7中,UdM和UMM分别为负荷处变流器的直流侧电压和交流侧相电压的峰值,UMMM为负荷端线电压有效值,电压单位均为kV。
采用基于稳定域边界二次逼近的暂态电压分析方法和时域仿真方法,其结果相对误差为-2.9%,处于工程允许的误差范围10%以内,说明上述裕度指标的有效性。

图4 故障切除时间为10.069 s时滑差S的时域仿真结果
Fig. 4 Time domain simulation of slip when fault is removed at 10.069 s

图5 故障切除时间为10.07 s时滑差S的时域仿真结果
Fig. 5 Time domain simulation of slip when fault is removed at 10.07 s

图6 故障切除时间为10.069 s时负荷处电压的时域仿真结果
Fig. 6 Time domain simulation of load voltage when fault is removed at 10.069 s

图7 故障切除时间为10.07 s时负荷处电压的时域仿真结果
Fig. 7 Time domain simulation of load voltage when fault is removed at 10.07 s
4 结论
(1) 建立了电力系统的数学模型,包括发电机、电动机和相应的变流器及其控制模型以及直流输电网络的模型。
(2) 通过识别给定故障的主导负荷母线,根据不同故障点采用不同等值方程,求解系统故障后的主导不平衡稳定点(CUEP),得出暂态电压稳定裕度指标。通过获取故障切除时的系统状态,准确、快速判断独立电力系统的暂态电压稳定。
参考文献:
[1] 马伟明. 舰船动力发展的方向-综合电力系统[J]. 海军工程大学学报, 2002, 14(6): 5-8.
MA Weiming. The direction of shipboard power development– integrated power system[J]. Journal of Naval University of Engineering, 2002, 14(6): 5-8.
[2] 杨秀霞, 张晓锋, 张毅. 舰船电力系统的发展趋势[J]. 中国修船, 2004, 17(3): 12-14.
YANG Xiuxia, ZHANG Xiaofeng, ZHANG Yi. The developing trend of shipboard power system[J]. China Shiprepair, 2004, 17(3): 12-14.
[3] MA Weiming. A survey of the second-generation vessel integrated power system[C]// APAP 2011 International Conference. Beijing, China, 2011: 1293-1302.
[4] 梅生伟, 刘锋, 薛安成. 电力系统暂态分析中的半张量积方法[M]. 北京: 清华大学出版社, 2010: 201.
MEI Shengwei, LIU Feng, XUE Ancheng. Tensor product method in power system transient analysis[M]. Beijing: Tsinghua University Press, 2010: 201.
[5] Potamianakis E G, Vournas C D. Short-term voltage instability: Effects on synchronous and induction machines[J]. IEEE Transactions on Power System, 2006, 21(2): 791-798.
[6] Diaz de Leon J A, Taylor C W. Understanding and solving short-term voltage stability problem[C]// Proceedings of IEEE Power Engineering Society Summer Meeting. Chicago, USA, 2002: 745-752.
[7] Guedes R B L, Martins A C P, Alberto L F C, et al. An extended energy function for voltage collapse analysis considering voltage dependent load models[C]// Power Tech Conference Proceedings of the IEEE. Bologna, Italy, 2003: 23-26.
[8] 叶俭, 梅生伟, 薛安成. 基于稳定域边界二阶逼近的暂态电压稳定分析[J]. 现代电力, 2005, 22(4): 1-6.
YE jian, MEI Shengwei, XUE Ancheng. Transient voltage stability analysis based on second-order approximation of stability boundary[J]. Modern Electric Power, 2005, 22(4): 1-6.
[9] 林舜江, 李欣然, 刘扬华, 等. 考虑负荷动态模型的暂态电压稳定快速判断方法[J]. 中国电机工程学报, 2009, 29(4): 14-20.
LIN Shunjiang, LI Xinran, LIU Yanghua, et al. Method for transient voltage stability quick judgment considering load dynamic model[J]. Proceedings of the CSEE, 2009, 29(4): 14-20.
[10] 汤涌. 电力系统电压稳定性分析[M]. 北京: 科学出版社, 2011: 46.
TANG Yong. Voltage stability analysis of power system[M]. Beijing: Science Press, 2011: 46.
[11] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002: 45-49.
NI Yixin, CHEN Shousun, ZHANG Baolin. Theory and analysis of dynamic power system[M]. Beijing: Tsinghua University Press, 2002: 45-49.
[12] 徐政. 交直流电力系统动态行为分析[M]. 北京: 机械工业出版社, 2005: 31-34.
XU Zheng. Dynamic behavior analysis of AC-DC power system[M]. Beijing: Mechanical Industry Press, 2005: 31-34.
[13] 林玉章, 蔡泽祥. 基于PEBS法的交直流输电系统暂态稳定分析[J]. 电力自动化设备, 2009, 29(1): 25-28.
LIN Yuzhang, CAI Zexiang. Transient stability analysis of AC/DC power system based on PEBS method[J]. Electric Power Automation Equipment, 2009, 29(1): 25-28.
[14] 余贻鑫, 王成山. 电力系统稳定性理论和方法[M]. 北京: 科学出版社, 1999: 30-35.
YU Yixin, WANG Chengshan. Theory and method of power system stability[M]. Beijing: Science Press, 1999: 30-35.
[15] Cheng D, Ma J. Calculation of stability region[C]// Proceedings of the 2003 (42nd) IEEE Conference on Decision and Control. Maui, USA, 2003: 5616-5620.
[16] Chiang H D, Chu C C, Cauley G. Direct stability analysis of electric power systems using energy functions: Theory, applications and perspective[J]. Proceedings of the IEEE, 1995, 83(11): 1497-1529.
(编辑 杨幼平)
收稿日期:2013-07-22;修回日期:2013-10-20
基金项目:国家自然科学基金资助项目(51177168)
通信作者:王新枝(1984-),男,江苏靖江人,博士,从事独立电力系统负载管理研究;电话:15172515394;E-mail: wangxzxm@gmail.com