泡沫金属双向承载的力学模型
刘培生
(北京师范大学 材料科学与工程系 射线束技术与材料改性教育部重点实验室, 北京100875)
摘 要: 根据开孔泡沫金属材料的结构特点提出其抽象化的新型简化结构模型, 即“八面体模型”, 在此基础上建立起该类材料在双向拉伸条件下的力学分析模型。 从该分析模型出发, 推导得出了该类材料在双向拉伸破坏时两向名义应力与孔率三者的数学关系式。 结果表明: 该关系式还可进一步描述成“偏应力”、 “平均应力”和孔率三者之间的关系。 本理论模型与Gibson和Ashby的有关理论体系的不同之处是, 前者可直接运用“梁理论”进行方便的分析和推演, 而后者则不能。 验证实验结果显示, 本理论模型的数学关系与实际数据吻合良好。
关键词: 泡沫金属; 多孔金属; 泡沫材料; 多孔材料 中图分类号: TB383
文献标识码: A
Mechanical model for metallic foams under biaxial loads
LIU Pei-sheng
(The Key Laboratory of Beam Technology and Material Modification of
Ministry of Education, Department of Materials Science and Engineering,
Beijing Normal University, Beijing 100875, China)
Abstract: Based on the structural feature of the open-cell metallic foam, an abstract and simplified structure model (i.e. the “octahedron model”) was put forward, and the mechanical model was further established for this three-dimensional reticulated high-porosity foam under biaxial tension. From this structure-property model, the mathematical relationship between biaxial nominal failure stresses and porosity was deduced and eventually derived for this material. This relationship can be further expressed as the mathematical relationship among the nominal failure “deviatoric stress”, the nominal failure “average stress” and porosity, but the concepts both of the “deviatoric stress” and the “average stress” can appear just from the mathematical treatment. Here, the difference of the present theoretical model from that presented by Gibson and Ashby is that, the former can directly use the “beam theory” conveniently whereas the latter can not. The results indicate that the mathematical relationship from the present model is in good agreement with the practical data.
Key words: foamed metal; metallic foam; porous material; porous metals
开孔泡沫金属是一类新型的多孔材料, 因其透过性(渗透性)好、 密度低、 比表面积大、 能量吸收性佳、 换热散热能力高、 吸声性好、 电磁波吸收性良、 阻焰、 耐热耐火、 抗热震、 气敏(一些多孔金属对某些气体十分敏感)、 能再生、 加工性好, 以及强韧性综合指标佳和可焊接等优良特性, 从而广泛地应用于航空航天、 电子与通讯、 原子能、 电化学、 石油化工、 交通运输、 冶金、 机械、 医学、 环保、 建筑等各种领域, 涉及流体分离过滤、 流体分布、 消音降噪、 吸能减震、 阻尼缓冲、 电磁屏蔽、 隔热阻火、 热交换和电化学过程等诸多方面的用途, 可制作过滤器、 流体分离器、 催化剂及催化剂载体、 隔音材料、 消音器、 能量吸收器、 减震缓冲器、 电磁屏蔽器件、 电磁兼容器件、 阻燃器、 换热器、 散热器, 以及多孔电极等[1-8]。 此外, 还可制作多种复合材料、 填充材料和轻质结构材料。 作为一种性能优秀的工程材料, 多孔泡沫金属的力学性能已受到研究者们的广泛关注[9-44], 并取得了许多成就。 在这些力学性能的研究中, 拉伸性能也是一个基本的指标。 实际工程应用中材料往往受到多向载荷, 故研究泡沫金属的双向和三向拉伸性能也就很有必要。 前人在该方面所作研究中具有代表性的主要是剑桥大学Ashby教授和麻省理工学院Gibson教授合作的工作[2, 13, 14], 但其合作建立的经典性理论模型[2]存在一些不足或应用困难问题[45, 46]。 关于多孔材料的另一模型是Kelvin的十四面体模型[2, 38], 而该模型则无论多孔体的受力状态是单向载荷还是双向和三向载荷, 均无法运用梁理论进行便捷的受力分析和进行有关的推演。 为此, 本文作者采取一种新的分析模型, 其在单向、 双向和三向载荷状态下均可方便地运用梁理论进行受力分析和推演。 本文作者利用该模型探讨了三维网状泡沫金属的双向拉伸性能, 采用梁理论得出该材料在双向拉伸破坏时两个外加名义应力与孔率三者之间的数学关系。 通过该关系式, 还可以换算出对应不同孔率值的泡沫金属所能承受的双向载荷水平。 这些似乎都是Gibson-Ashby理论体系所难于或不便于实现的。
1 分析模型的基本假设(“八面体模型”)
结构均匀、 各向同性的三维网状多孔金属材料, 系由固态金属棱柱(孔筋)和连通性孔隙构成。 为简化其拉伸性能分析, 可将构成多孔体的这些棱柱视为规则地按立方体对角线方式连接, 从而形成大量正交密积的体心立方式八面体孔隙单元(见图1)。 这些密积的单元八面体构成整个多孔泡沫体。 这种八面体模型构架的每条棱边(棱柱)是完全等价的, 能较好地实现三维同性的理想特点, 并可进行规则而均匀的三维延伸扩展, 在三个相互垂直的轴向上形成大量不同方向上的八面体结构单元则相互密积, 从而形成三维各向同性的均匀三维网络结构体。 由于工艺的圆整性, 棱柱汇合处结点的承载能力一般大于棱柱体本身, 故断裂破坏一般发生在棱柱上。 棱柱内部任何位置产生的最大正应力(最大拉应力)达到对应密实材料的抗拉强度(σ0)大小时, 都会导致造成多孔体整体破坏的断裂出现。
本模型可克服Gibson-Ashby模型[2, 13, 14]中的若干缺点, 如孔隙单元的密堆积问题、 模型中棱柱的结构等价问题、 模型中棱柱的受力状态等价问题以及非单向承载时的棱柱受力分析问题等[45, 46]。 实际的泡沫多孔材料的孔隙结构是极其复杂的, 无论是Gibson和Ashby的立方体模型, 还是Kelvin的十四面体模型[2, 46]和作者的八面体模型, 都不可能完整而全面地描写多孔材料的实际孔隙状态(而实际上要做到这一点的必要性也并不是很大)。 众所周知, 任何理论模型都是在一定程度上对实际状态的抽象和综合概括, 其目的都是在尽量简化的基础上简捷而方便地表征出实际状态的有效特征和性能行为。 要评价这些模型是否过于简化和是否实用, 关键是看其是否能够较好地表征出泡沫材料的结构特点, 更重要的是看其是否能够从相应的几何模型便捷地推演出符合多孔材料实测性能结果的对应实用性数理表征模型。
2 关系式的推导
上述多孔体内的单元八面体排列规则、 分布均匀, 故在受到外加载荷时其受力也均匀。
在多孔体受到双向拉伸力时, 意味着其内部单元八面体中的棱柱也会受到载荷的作用, 从而产生偏转或具有偏转的趋势。 因此, 为简化推导过程起见, 不妨先将棱柱作脆性悬壁梁受力分析。 当然, 这种处理仅仅是解决本文问题的一种分析方式, 且该方式已在单向拉伸分析时被证明可行, 但最终评判其可行性和合理性则仍有待于后面相关的实验结果来检验。 由于本模型中的棱柱无论在结构上还是在受力状态上都是完全等价, 因此任何一条棱柱均可表征其它棱柱。 如图1所示, 可将其中某一棱柱(AB)隔离出来作受力分析, 并假定侧结点(A)固定而顶结点(B)受外加载荷作用。 对于密积中的单元八面体, 其每一棱柱为3个八面体单元所共用。 而在图1的双向拉伸受力分析中, 仅考虑有轴向拉伸力的单元。 即对图1中棱柱(AB)而言, 只考虑图中示出的主单元(其轴向与外加载荷σ1方向一致)和主单元左上角的副单元(其轴向与外加载荷σ2方向一致)。 下面的推演过程基于棱柱的“脆性破坏”假设, 且由细梁理论可忽略剪切应力的影响。

图1 八面体模型受力分析图(每条棱柱均为3个轴向相互垂直的八面体结构单元所共用)
Fig.1 Octahedron unit under biaxial loading for isotropic metal foams
设包容单元八面体的立方体边长为a, 则棱柱(AB)顶端(B)所受外力。
1) 竖向力为

2) 水平力为

3) 合力为

设合力F与σ1的夹角为α1, 则由式(1)~(3)可得

过A点作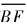 的平行线与包容八面体的立方形上棱边交于D点(见图1), 则由式(4)、 (5)可得:
的平行线与包容八面体的立方形上棱边交于D点(见图1), 则由式(4)、 (5)可得:

又

由式(7)和(8)结合余弦定理(参见图1)得:
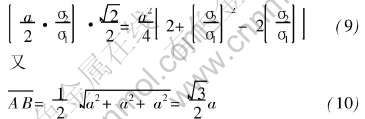
设 与
与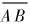 的夹角为α2, 则由式(6)、 (9)和(10)结合余弦定理(见图1)可得:
的夹角为α2, 则由式(6)、 (9)和(10)结合余弦定理(见图1)可得:

由式(3)、 (11)和(12)结合图1, 得棱柱(AB)所受外加力。
1) 横向力为

又由有关几何运算可得棱柱的抗弯截面模量为[25]
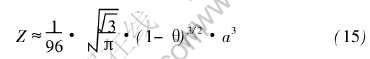
式中 θ为多孔体的孔率。
由式(13)和(15)可得弯矩引起的最大正应力为

又由文献[25]给出棱柱的横截面积为
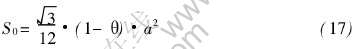
故从式(14)和(17)可得出轴向力F2产生的轴向拉应力为

由式(16)和(18)可知, 棱柱所受最大正应力为

从上面的推演过程可知, 棱柱的轴向压缩可不予考虑。
3 模型关系式的修正
上述推导是在理想的简化状态下进行的, 而实际情况则较为复杂。 因此, 多孔体在双向拉伸过程中实际产生的最大应力, 就应该在上述理论导出的的σmax基础上加以修正。 最简单的修正方法, 就是在该σmax前加一表征多孔体材质种类和制备工艺条件的修正系数k(该系数包括材质种类、 材质缺陷、 孔隙具体形状和大小分布等因素的综合作用), 即实际最大应力σmax为
σmax≈k·σmax
通过以上推导和分析, 可以得出如下关于多孔体在双向拉伸破坏时两向名义应力关系式

式中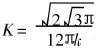 , 实际上是一个材料常数。 它和k一样, 也取决于多孔体的材质种类和制备工艺条件。
, 实际上是一个材料常数。 它和k一样, 也取决于多孔体的材质种类和制备工艺条件。
上述推导是以脆性断裂为基础的。 为适应于多种断裂方式, 根据文献[25, 37, 43]的有关内容, 可将上式写成更一般的形式:
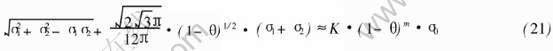
式中 m为对应致密材料的塑脆性指标, 介于1~1.5(即3/2)之间[25, 37, 43]: 当对应致密材料的脆性很高时, m偏向1.5; 当对应致密材料的塑性很高时, m偏向1; 当对应致密材料为塑性适中的一般金属或合金时, m可近似取1.25, 比如金属镍。 即对于塑性与泡沫镍相当的泡沫金属, 近似有:

在多孔体双向承载的条件下, 相当于在三维空间内有两个方向的载荷不为零, 而第三个方向的载荷为零, 即有一个主应力为零: σ1≠0, σ2≠0, σ3=0。 此时利用偏应力σd的概念, 则

当双向承受的名义应力相等, 即σ1=σ2=σ时, 式(22)化为

式中 σ为泡沫金属在双向等荷承载条件下的载荷强度。
4 模型关系式的实验验证和结果
实验材料采用电沉积法制备的泡沫镍板[47], 其厚度为2~3mm, 孔率在89%~99%之间。 双向拉伸试样为简单的正十字型, 可夹持宽度为60mm[36, 37, 43]。 拉伸测试设备采用配置计算机数据记录系统的PLS-S100型双轴拉伸试验机, 加载误差≤1%, 拉伸速度在6.5~9.0mm/min之间的范围内调整, 以测出双轴等速拉伸和双轴异速拉伸等不同组合态拉伸断裂时的双向拉力, 进而换算出此时两个方向的名义承载应力。 整个测试在25℃左右的室温下进行。 实验观察和电脑记录表明, 在样品开始断裂瞬间, 双向拉力几乎同时达到最大值, 然后随裂口的增大而减小。 测试结果列于表1。 表中σx(σ1)和σy(σ2)分别是根据多孔体破裂时双向拉伸试验机在x轴和y轴两个方向测到的最大拉力换算出来的名义应力值。
由文献[48]可查得金属镍的抗拉强度为317MPa。 将σ0=317MPa以及表1中的有关实验数据代入式(22), 换算出其相应的常数值, 并将求得的常数值一同列于表1(表中用括号标出的是按格拉布斯统计法则检出的异常可疑数据)。 为便于比较分析, 表中还给出了不同样品常数值对其平均值的相对波动幅。 从表1有关数据可知, 式(22)的常数项相对波动幅平均为6.6%, 是一个较小的量。 可见该式常数项的稳定性较高, 可较好地表达泡沫金属在双向拉抻过程中所表现出来的有关量值关系。 当然, 实际泡沫体的结构型式和内在特点远比理想模型复杂。
不过, 表1数据也显示, 式(22)的修正系数0.329远离于1。 这主要是由于直接将手册中查出的数据σ0=317MPa作为泡沫镍中实际棱柱的抗拉强度, 代入公式而计算出来的。 317MPa这个数据对应的是相对完整的纯镍晶体, 而泡沫镍材料的实际棱柱则含有各种缺陷, 其真实的抗拉强度会远小于此值。 但是, 这些并不影响上述的数理关系, 因为这种偏差可统一消化于修正系数K和σ0的乘积中。
5 结论
1) 开孔泡沫金属在双向拉伸破坏时两向名义应力的数学关系可表征为

式中 σ1和σ2分别为双向加载状态下拉伸破坏时的两向名义应力, σ0为对应致密材料的抗拉强度, θ为多孔体的孔率。 K为一个材料常数, 它表征多孔体材质种类和制备工艺条件, 因而集中了材质种类、 材质缺陷、 孔隙具体形状和大小分布等因素的综合作用。 进一步表达成偏应力和平均应力的简单形式, 即有

2) 经相关实验的实际检验, 证明该模型理论具有良好的实用性, 而且其应用效果好于Gibson和Ashby等合作建立的经典性模型体系。 由于本文
表1 实验结果和式(22)计算值
Table 1 Experimental results and relative values of formula (22)

作者迄今未发现在Gibson和Ashby等所发表的论著中出现可供计算的有关具体数据, 因此目前尚无法利用他们本身的工作结果对其模型体系与本文作者的模型体系进行大量而系统的应用对比。 然而, 本文模型在多孔体的受力分析方面, 其单、 双向载荷状态分析方式的一贯性和便捷性, 却是明显地优于Gibson-Ashby理论体系的。 此外, 本模型还可延伸到三向受力状态(含拉伸和压缩)下的分析, 从而得到相应的关系公式, 这项工作拟待下一步进行。
REFERENCES
[1]刘培生. 多孔材料引论[M]. 北京: 清华大学出版社, 2004.
LIU Pei-sheng. Introduction to Porous Materials[M]. Beijing: Tsinghua University Press, 2004.
[2]Gibson L J, Ashby M F. 多孔固体结构与性能[M]. 刘培生, 译. 北京, 清华大学出版社, 2003.
Gibson L J, Ashby M F. Cellular Solids: Structure and Properties[M]. LIU Pei-sheng, transl. Beijing: Tsinghua University Press, 2003.
[3]Banhart J. Manufacture, characterisation and application of cellular metals and metal foams[J]. Progress in Materials Science, 2001, 46: 559-632.
[4]黄培云. 粉末冶金原理(第2版)[M]. 北京: 冶金工业出版社, 1997. 382-386.
HUANG Pei-yun. Principles of Powder Metallurgy[M]. Beijing: Metallurgical Industry Press, 1997. 382-386.
[5]汤慧萍, 张正德. 金属多孔材料发展现状[J]. 稀有金属材料与工程, 1997, 26(1): 1-6.
TANG Hui-ping, ZHANG Zheng-de. Developmental states of porous metal materials[J]. Rare Metal Materials and Engineering, 1997, 26(1): 1-6.
[6]Liu P S, Liang K M. Functional materials of porous metals made by P/M, electroplating and some other techniques[J]. J Mater Sci, 2001, 36: 5059-5072.
[7]Liu P S, Yu B, Hu A M, et al. Development in applications of porous metals[J]. Trans Nonferrous Met Soc China, 2001, 11(5): 629-638.
[8]许庆彦, 陈玉勇, 李庆春. 多孔铝合金材料吸声性能的研究[J]. 宇航材料工艺, 1998(2): 39-43.
XU Qing-yan, CHEN Yu-yong, LI Qing-chun. Aerospace Materials Technology, 1998(2): 39-43.
[9]Liu P S, Sang H B. Mechanical property of foamed metals[J]. Int J Iron & Steel Res, 2004, 11(3): 53-58.
[10]刘培生. 泡沫金属力学性能的若干问题[J]. 稀有金属材料与工程, 2004, 33(5): 473-477.
LIU Pei-sheng. Some problems on mechanical properties of foamed metals[J]. Rare Metal Materials and Engineering, 2004, 33(5): 473-477.
[11]Ashby M F, Evans A, Fleck N A, et al. Metal Foams: A Design Guide[M]. Boston: Elsevier Science, 2000. 80-112.
[12]Hamiuddin M. Correction between mechanical properties and porosity of sintered iron and steels[J]. Powder Metall Int, 1986, 18(2): 73-76.
[13]Gibson L J, Ashby M F, Zhang J, et al. Failure surfaces for cellular materials under multiaxial loads(Ⅰ)—Modelling[J]. Int J Mech Sci, 1989, 31(9): 635-663.
[14]Triantafillou T C, Zhang J, Shercliff T L, et al. Failure surfaces for cellular materials under multiaxial loads(Ⅱ)—Comparison of models with experiment[J]. In J Mech Sci, 1989, 31(9): 665-678.
[15]Nagaki S, Sowerby R, Goya M. An anisotropic yield function for porous metal[J]. Mater Sci Eng A, 1991, A142: 163-168.
[16]李雅文, 丁华东, 浩宏奇, 等. 铜石墨材料抗弯强度与断裂机制研究[J]. 兵器材料科学与工程, 1997, 20(3): 14-18, 38.
LI Ya-wen, DING Hua-dong, HAO Hong-qi, et al. Study of bending strengh and fracture mechanism of copper-graphite material[J]. Ordnance Material Science and Engineering, 1997, 20(3): 14-18, 38.
[17]Silva M G da, Ramesh K T. The rate-dependent deformation and localization of fully dense and porous Ti-6Al-4V[J]. Mater Sci Eng A, 1997, A232: 11-22.
[18]Beatls J T, Thompson M S. Density gradient effects on aluminum foam compression behavior[J]. Journal of Materials Science, 1997, 32: 3595-3600.
[19]Simone A E, Gibson L J. Efficient structural components using porous metals[J]. Mater Sci Eng A, 1997, A229: 55-62.
[20]赵增典, 张勇, 苗汇静. 泡沫铝合金的抗压强度与吸声性能比较[J]. 机械工程材料, 1998, 22(2): 53-54.
ZHAO Zeng-dian, ZHANG Yong, MAO Hui-jing. Comparison of the compressive strength with the sound absorption properties of aluminum foam[J]. Machinery Engineering Materials, 1998, 22(2): 53-54.
[21]Andrews E, Sanders W, Gibson L J. Compressive and tensile behavior of aluminum foams[J]. Mater Sci Eng A, 1999, A270: 113-124.
[22]Fusheng H, Zheng Z. The mechanical behavior of foamed aluminum[J]. Journal of Materials Science, 1999, 34: 291-299.
[23]Liu P S, Fu C, Li T F, et al. Relationship between tensile strength and porosity for high porosity materials[J]. Science in China, 1999, 42(1): 100-107.
[24]Liu P S, Fu C, Li T F. Approximate means for evaluating tensile strength of high porosity materials[J]. Trans Nonferrous Met Soc China, 1999, 9(3): 546-552.
[25]Liu P S. The tensile strength of porous metals with high porosity[J]. J Adv Mater, 2000, 32(2): 9-16.
[26]Nieh T G, Higashi K, Wadsworth J. Effect of cell morphology on the compressive properties of open-cell aluminum foams[J]. Materials Science and Engineering A, 2000, 283: 105-110.
[27]Kanahashi H, Mukai T, Yamada Y, et al. Dynamic compression of an ultra-low density aluminum foam[J]. Mater Sci Eng A, 2000, A280: 349-353.
[28]Badiche X, Forest S, Guibert T, et al. Mechanical properties and non-homogeneous deformation of open-cell nickel foams: application of the mechanics of cellular solids and of porous materials[J]. Mater Sci Eng A, 2000, A289: 276-288.
[29]刘培生, 梁开明, 顾守仁, 等. 多孔金属抗拉强度公式中的指数项取值[J]. 力学学报, 2001, 33(6): 853-855.
LIU Pei-sheng, LIANG Kai-ming, GU Sou-ren, et al. The exponential item in formulas for calculating tensile strength of porous metals[J]. Acta Mechanica Sinica, 2001, 33(6): 853-855.
[30]Hyun S K. Murakami K, Nakajima H. Anisotropic mechanical properties of porous copper fabricated unidirectional solidification[J]. Mater Sci Eng A, 2001, A299: 241-248.
[31]Park C, Nutt S R. Strain rate sensitivity and defects in steel foam[J]. Mater Sci Eng A, 2002, A323: 358-366.
[32]Benouali A H, Froyen L, Delerue J F, et al. Mechanical analysis and microstructural characterisation of metal foams[J]. Mater Sci Technol, 2002, 18(5): 489-494.
[33]程和法, 黄笑梅, 许铃. 基体对泡沫铝压缩行为与吸能性的影响[J]. 有色金属, 2003, 55(3): 10-22.
CHENG He-fa, HUANG Xiao-mei, XU Ling. Effect of matrix properties on compressive behavior and energy absorption of foamed al alloys[J]. Nonferrous Metals, 2003, 55(3): 10-22.
[34]刘建秀, 肖玲, 韩长生. 冲击载荷下铜基粉末冶金(Cu-PM)多孔材料的动态应力-应变特性研究[J]. 材料科学与工程学报, 2003, 21(6): 869-871.
LIU Jian-xiu, XIAO Ling, HAN Chang-sheng. Stress-strain properties of Cu-matrix powder metallurgy( Cu-PM) porous material under shock[J]. Journal of Material Science and Engineering, 2003, 21(6): 869-871.
[35]程和法, 黄笑梅, 许玲. 泡沫铝的动态压缩性能和吸能性研究[J]. 兵器材料科学与工程, 2003, 26(5): 37-43.
CHENG He-fa, HUANG Xiao-mei, XU Ling. Research on dynamic compressive properties and energy absorption of aluminum foam[J]. Ordnance Material Science and Engineering, 2003, 26(5): 37-43.
[36]刘培生, 王习术. 泡沫金属双向等速拉伸载荷强度与孔率的近似关系[J]. 稀有金属材料与工程, 2003, 32(8): 624-626.
LIU Pei-sheng, WANG Xi-shu. Approximate relationship between strength and porosity in foamed metals for equal-speed biaxial tension[J]. Rare Metal Materials and Engineering, 2003, 32(8): 624-626.
[37]刘培生. 泡沫金属双向拉伸破坏时名义应力与孔率的关系[J]. 中国科学E, 2003, 33(9): 774-777.
LIU Pei-sheng. Relationship between fracturing nominal stress and porosity for metal foams under biaxial tension[J]. Science in China E, 2003, 33(9): 774-777.
[38]Kwon Y W, Cooke R E, Park C. Representative unite-cell models for open-cell metal foams with or without elastic filler[J]. Mater Sci Eng A, 2003, A343: 63-70.
[39]Sanders W S, Gibson L J. Mechanics of BCC and FCC hollow-sphere foams[J]. Mater Sci Eng A, 2003, A352 (1-2): 150-161.
[40]Sanders W S, Gibson L J. Mechanics of hollow sphere foams[J]. Mater Sci Eng A, 2003, A347 (1-2): 70-85.
[41]Choe H, Dunand D C. Mechanical properties of oxidation-resistant Ni-Cr foams[J]. Mater Sci Eng A, 2004, A384 (1-2): 184-193.
[42]Liu P S. Tensile fracture behavior of foamed metallic materials[J]. Mater Sci Eng A, 2004, 384(1-2): 352-354.
[43]Liu P S. Different theories application to foamed metals under biaxial equal-stress tension[J]. Mater Sci Eng A, 2004, A364: 370-373.
[44]Liu P S. Effect of preparation conditions on relative elongation of nickel foam[J]. Mater Sci Technol, 2004, 20(5): 669-672.
[45]刘培生. 泡沫金属的经典性模型[J]. 有色金属, 2005, 57(2): 55-57.
LIU Pei-sheng. Basic analysis to classical model for foamed metals[J]. Nonferrous Metals, 2005, 57(2): 55-57.
[46]刘培生. 关于多孔材料的新模型[J]. 材料研究学报, 2006, 20(6): 64-68.
LIU Pei-sheng. A new model for porous materials[J]. Chinese Journal of Materials Research, 2006, 20(6): 64-68.
[47]Liu P S, Liang K M. Preparation and corresponding structure of nickel foam[J]. Mater Sci Technol, 2000, 16(5): 575-578.
[48]美国金属学会. 金属手册(第2卷)[M]. 第9版. 北京: 机械工业出版社, 1994. 987.
American Society for Metals. Metals Handbook(Vol 2)[M]. 9th ed. Beijing: China Machine Industry Press, 1994. 987.
(编辑陈爱华)
基金项目: 国家自然科学基金资助项目(50201003)
收稿日期: 2005-09-06; 修订日期: 2005-12-20
通讯作者: 刘培生, 电话: 010-62205350; E-mail: liu996@263.net