基于模糊逻辑的永磁同步电机调速方法设计与分析
于双和1,杜佳璐1,周丽娜1,杨振强2
(1. 大连海事大学 信息科学技术学院,辽宁 大连,116026;
2. 大连理工大学 电气工程学院,辽宁 大连,116024)
摘要:针对永磁同步电机调速问题的非线性、多变量、强耦合等特征,分别设计自适应模糊PI控制器和自重构模糊控制器。在矢量PI控制基础上设计永磁同步电机自适应模糊PI控制器,进而设计辅以切换策略的自构模糊控制器以有效地克服参数突变和负载扰动的影响,提高系统鲁棒性、快速性,并实现控制器参数的在线调整。仿真结果表明自适应模糊PI控制性能优于传统的PI控制,同时自重构模糊控制优于固定结构模糊控制。
关键词:模糊PI控制;自构模糊控制;切换策略;永磁同步电机
中图分类号:TP271+61 文献标志码:A 文章编号:1672-7207(2011)S1-1032-05
Design and analysis of speed regulation of permanent magnet synchronous motor based on fuzzy logic
YU Shuang-he1, DU Jia-lu1, ZHOU Li-na1, YANG Zhen-qiang2
(1. School of Information Science and Technology, Dalian Maritime University, Dalian 116026, China;
2. School of Electrical Engineering, Dalian University of Technology, Dalian 116024, China)
Abstract: According to the nonlinear, multi-variable and strong coupled speed regulation problem of permanent magnet synchronous motor (PMSM), the adaptive fuzzy PI control and self-reconstructed fuzzy control were designed respectively. Based on the vector control of PMSM, the adaptive fuzzy PI control was firstly designed, and then the self-reconstructed fuzzy control with switching strategy was designed to overcome the parameter variation and load disturbance effectively. The proposed controllers can be adjusted online with improved robustness and fast response. Simulation results demonstrate that the proposed strategies are superior to the conventional PI control and fixed structure fuzzy control.
Key words: fuzzy PI control; self-reconstructed fuzzy control; switching strategy; PMSM
随着交流变频技术的发展,永磁同步电机在机器人和数控机床等领域的交流伺服系统中越来越显示出优越性,如更高的调速精度、更大的调速范围以及更快的响应速度等[1]。然而永磁同步电机其自身就具有非线性、强耦合性和时变性,加之系统运行时还会受到不同程度的外部干扰,使得常规控制策略很难满足高性能永磁同步电机伺服系统的控制要求[2]。矢量控制广泛应用到永磁同步电机的定位或调速任务中,且广泛采用线性PI算法,通常难以达到理想的控制效 果[3]。随着控制理论的发展,智能控制如模糊逻辑、神经网络等使得伺服运动系统获得了更好的控制性 能[4-6]。永磁同步电机的动态特性受到内部参数和负载变化的影响,很难建立精确的数学模型。而模糊控制设计不需要精确的数学模型,因此具有较强的鲁棒性,能够很好地克服伺服系统中模型参数变化和非线性等不确定因素。而模糊自适应控制器可实现在线调整参数,能获得良好的控制效果。本文将在永磁同步电机矢量控制的基础上引入自适应模糊控制,进而采用自重构和切换策略,并与传统矢量控制和固定结构的模糊控制进行比较,以显示在自适应性、抗干扰和鲁棒性等控制品质的改善。
1 永磁同步电机的数学模型
在忽略铁心损耗和磁路饱和、定子三相绕组在空间对称分布、气隙磁场和磁密在空间为正弦分布情况下,永磁同步电机调速系统数学模型可表示如下。
(1) 电压方程
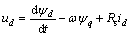 (1)
(1)
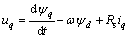 (2)
(2)
(2) 磁链方程
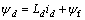 (3)
(3)
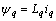 (4)
(4)
(3) 转矩方程
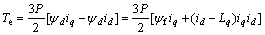 (5)
(5)
(4) 机械运动方程
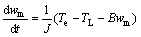 (6)
(6)
式中:ud和uq为定子电压d-q轴分量;id和iq为定子电流d-q轴分量;Ld和Lq是d-q轴自感;ψd和ψq为定子磁链d-q轴分量;ψf为转子永磁体产生的磁链;Rs为定子电阻;T e为电机电磁转矩;TL是负载转矩;ωm为转子角速度;p是极对数;ω=Pωm为转子电角速度;J为转动惯量;B为摩擦因数。从式(6)可看出:永磁同步电机数学模型是多变量、非线性的,含有定子电流分量id,iq以及机械角速度ωm的乘积。
2 自适应模糊PI控制
在永磁同步电机矢量PI控制调速系统的基础上,建立了永磁同步电机自适应模糊PI控制系。系统采用速度环和电流环双闭环控制,电流环采用PI控制器,速度环采用自适应模糊PI控制器。以转速误差e及其变化率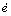 作为输入变量,以PI参数的变化量
作为输入变量,以PI参数的变化量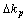 和
和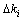 为输出的两输入两输出控制器。首先找出PI 2个参数kp,ki与e和
为输出的两输入两输出控制器。首先找出PI 2个参数kp,ki与e和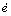 之间的关系,建立模糊规则表。k p1,k i1是模糊控制器的量化因子。转速的误差e及其变化率
之间的关系,建立模糊规则表。k p1,k i1是模糊控制器的量化因子。转速的误差e及其变化率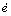 以及输出
以及输出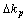 ,
,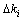 的变化范围都定义为模糊集上的目标论域:
的变化范围都定义为模糊集上的目标论域:
e, 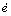 ={-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6};
={-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6};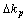 ,
,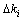 ={-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7}。
={-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7}。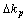 ,
,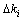 和e,
和e,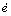 模糊子集为{NB, NM, NS, ZO, PS, PM, PB},其子集元素分别代表负大、负中、负小、零、正小、正中、正大。e的真实论域为[-1 500, 1 500],所以其量化因子k p1=6/1 500,而
模糊子集为{NB, NM, NS, ZO, PS, PM, PB},其子集元素分别代表负大、负中、负小、零、正小、正中、正大。e的真实论域为[-1 500, 1 500],所以其量化因子k p1=6/1 500,而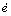 的真实论域为 [-10 000, 10 000],其量化因子k i1=6/10 000。
的真实论域为 [-10 000, 10 000],其量化因子k i1=6/10 000。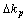 ,
,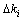 和e,
和e,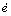 均服从三角型隶属函数曲线分布,由此可计算出各模糊子集的隶属度,根据模糊推理来对PI 2个参数进行在线修正。
均服从三角型隶属函数曲线分布,由此可计算出各模糊子集的隶属度,根据模糊推理来对PI 2个参数进行在线修正。
3 自构模糊控制
在自构模糊控制系统中,模糊逻辑部分的模糊规则采用以下形式:
Rj:if x1 is 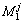 and
and xn is
xn is 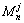 then y is Sj
then y is Sj
其中:Rj为第j个模糊规则;xi和y分别为输入和输出变量;n为外部输入变量的个数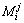 为第j个规则的模糊集合;Sj为该模糊系统的输出。
为第j个规则的模糊集合;Sj为该模糊系统的输出。
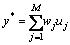 (7)
(7)
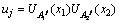 (8)
(8)
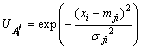 (9)
(9)
式中:xi为输入变量;x1=e (速度误差信号),x2=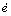 (速度误差变化率),σji和mji分别为隶属度函数层中输入变量xi所对应的第j个高斯函数的标准差和均值。
(速度误差变化率),σji和mji分别为隶属度函数层中输入变量xi所对应的第j个高斯函数的标准差和均值。
自构模糊控制的学习过程包括2类:第1类是结构学习,结构学习是使第2层寻找到合适的隶属函数,并使规则层隶属函数数目最少;第2类是参数学习,基于反向传播法来修正规则层与输出层间的连接权值,还有隶属度函数的参数值,以使给定的误差能量函数达到最小。
3.1 结构学习
在结构学习过程中,首先要确定是否需要执行结构学习。若emin≤|e|或者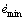 ≤|
≤|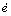 |,这里的emin和
|,这里的emin和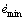 为预设的正值常数,若满足此条件则需要执行结构学习。下一步决定是否要在隶属函数层和规则层分别增加新的隶属函数。若在规则层增加了一个新的隶属函数就意味着增加了一个新的模糊规则,而此时,其规则层的输出可以理解成对应的输入信号属于整个输出群组的程度。规则层的输出可用来定义输出强度测量函数:
为预设的正值常数,若满足此条件则需要执行结构学习。下一步决定是否要在隶属函数层和规则层分别增加新的隶属函数。若在规则层增加了一个新的隶属函数就意味着增加了一个新的模糊规则,而此时,其规则层的输出可以理解成对应的输入信号属于整个输出群组的程度。规则层的输出可用来定义输出强度测量函数:
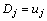 j=1, 2, …, M(k) (10)
j=1, 2, …, M(k) (10)
式中:M(k)为当时已存在的模糊规则数目。取Dj的最大值Dmax,即
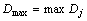 j=1, 2, …, M(k) (11)
j=1, 2, …, M(k) (11)
如果Dmax≤ ,那么系统将产生一个新的模糊规则,则隶属层相应有新的隶属函数产生。这里
,那么系统将产生一个新的模糊规则,则隶属层相应有新的隶属函数产生。这里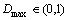 ,为预设的临界值,用来限定自构模糊系统的大小。新的隶属函数的均值与标准差将分别被赋予预先设定的初始值
,为预设的临界值,用来限定自构模糊系统的大小。新的隶属函数的均值与标准差将分别被赋予预先设定的初始值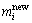 和
和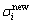 。为防止新产生的隶属函数与已存在的隶属函数过于相似,用一种相似度检测的方法对各隶属函数之间的相似程度进行判定。假设2个模糊集合M和N,各自的隶属函数为:
。为防止新产生的隶属函数与已存在的隶属函数过于相似,用一种相似度检测的方法对各隶属函数之间的相似程度进行判定。假设2个模糊集合M和N,各自的隶属函数为:
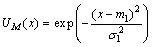
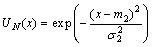
令m1≥m2,设
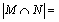
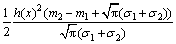 +
+
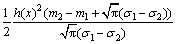 +
+
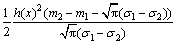 (12)
(12)
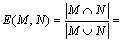
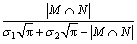 (13)
(13)
式中:h(x)=max{0, x},m2,m1和σ1,σ2分别为M和N的隶属函数的均值和标准差。利用该相似度检测法,将新产生的隶属函数与己有隶属函数进行相似度测量有:
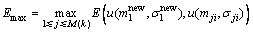 (14)
(14)
式中: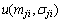 为高斯隶属函数;mji,σji分别为该隶属函数的均值和标准差;M是第i个输入信号隶属函数的数目。如果Emax≤
为高斯隶属函数;mji,σji分别为该隶属函数的均值和标准差;M是第i个输入信号隶属函数的数目。如果Emax≤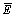 ,
,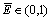 ,
,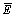 为预先设定的值,则新的隶属函数将被采用,有
为预先设定的值,则新的隶属函数将被采用,有
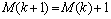 (15)
(15)
当一个新的模糊规则产生时,在新的模糊规则与输出层之间将产生一个新的连接权值wnew,wnew为预先设定值或是随机值。
3.2 切换策略
由于被控对象的动态不确定性,如内部参数变化和外部扰动等等,在参数学习过程中很难精确算出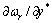 项。为了克服这个问题并加快模糊系统中参数的学习效率,采用切换策略来选择一个合适的误 差项。
项。为了克服这个问题并加快模糊系统中参数的学习效率,采用切换策略来选择一个合适的误 差项。
定义跟踪误差向量如下:
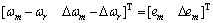 (16)
(16)
定义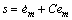 ,且C>0。
,且C>0。
(1) 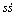 >0,这种情况是切换条件未得到满足,则使控制器的输出为s。
>0,这种情况是切换条件未得到满足,则使控制器的输出为s。
(2) 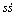 <0,这种情况是切换条件得到满足,则使控制器的输出为
<0,这种情况是切换条件得到满足,则使控制器的输出为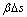 ,这里
,这里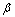 是任意很小的正数。
是任意很小的正数。
为了对自构网络中的参数进行调整,我们定义策略切换控制器的函数Ei,
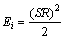 (17)
(17)
式中:SR为切换策略控制器的输出。依然有2种情况,如下所述:
(1) 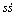 ≥0,切换条件未得到满足,此时的误差项为
≥0,切换条件未得到满足,此时的误差项为
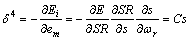 (18)
(18)
(2) 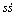 <0,切换条件得到满足,此时的误差项为
<0,切换条件得到满足,此时的误差项为
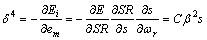 (19)
(19)
这样,利用切换策略控制器获得了比较合适的误差项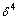 。将此误差项反向传播,并运用梯度下降法使Ei函数达到最小,以调整各连接权值。
。将此误差项反向传播,并运用梯度下降法使Ei函数达到最小,以调整各连接权值。
4 仿真结果与分析
4.1 自适应模糊PI控制
采用表1所给定参数的永磁同步电机,自适应模糊PI控制系统采用连续仿真,给定转速为1 200 r/min。电磁转矩Te在0.03 s由0.1 N/m突变为1 N/m。自适应模糊PI控制与传统PI控制系统仿真图的比较如图1所示。
分析仿真实验图可得:在上升时间相同的情况下,自适应模糊PI控制系统与传统PI控制系统相比,转速曲线无震荡,且不出现超调或超调量非常小。当电机的电磁转矩突然变化时,自适应模糊PI控制系统的电机转速平稳无超调,而传统PI控制系统转速响应出现较大的超调量。这是因为,当负载发生变化时,传统的PI控制器参数要重新进行计算和整定,而自适应模糊PI控制系统中的模糊控制器在电机运行中,实时检测电机转速和给定值之间的误差e及其误差变化率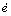 ,并通过模糊控制规则在线调整推理出相应的PI控制器参数,从而实现了变参数的PI控制。使电机调速系统具有上升时间短、无超调、鲁棒性强的动态性能。
,并通过模糊控制规则在线调整推理出相应的PI控制器参数,从而实现了变参数的PI控制。使电机调速系统具有上升时间短、无超调、鲁棒性强的动态性能。
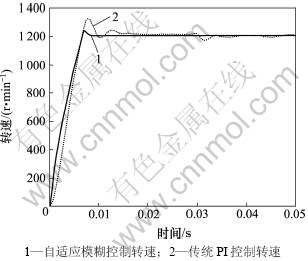
图1 传统PI控制与自适应模糊PI转速响应曲线
Fig.1 Speed curves of traditional PI control and adaptive fuzzy PI control
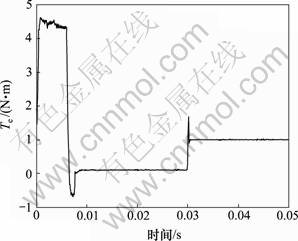
图2 自适应模糊PI控制转矩响应曲线
Fig.2 Electromagnetic torque curve of adaptive fuzzy PI control
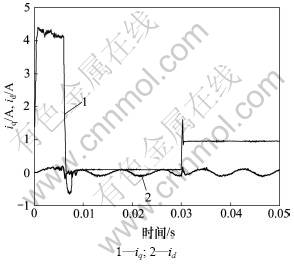
图3 自适应模糊PI控制的d-q轴电流
Fig.3 d-q axis current curve of fuzzy adaptive PI control
4.2 自构模糊控制
对于同样的永磁同步电机,仿真时给定转速为 1 200 r/min。电磁转矩Te在0.03 s由0.01 N/m突变为0.5 N/m,使用切换策略和未使用切换策略的转速响应曲线如图6所示。
由图6可知:二者的上升时间相同的情况下,未使用切换策略的系统产生了较大的超调,且在转矩突变时,转速有较大的波动,该波动持续时间长,系统恢复稳定的用时也相对较长。而使用切换策略的系统的转速响应抗干扰能力较强,受到干扰后能尽快跟踪给定转速并再次稳定。
表1 永磁同步电机的参数
Table 1 Parameters of PMSM

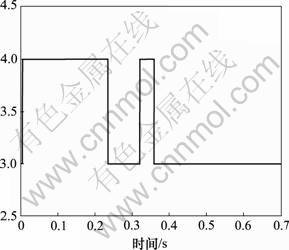
图4 自构模糊神经网络的规则变化
Fig.4 Number of rules in self-control fuzzy neural network
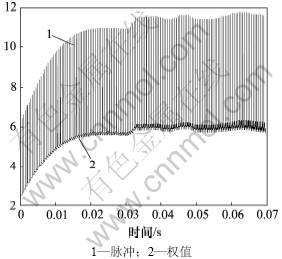
图5 输出权值学习过程
Fig.5 Parameter learning process in weight value in output layer
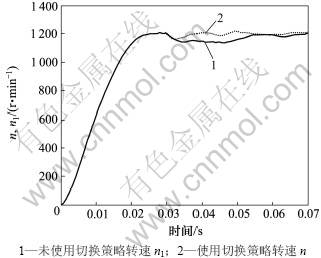
图6 使用切换策略和未使用的转速响应曲线
Fig.6 Speed curves of using and not using switching strategy
6 总结
基于矢量控制的PI调速原理里,设计和分析了自适应模糊PI控制器和自构模糊控制的器,并进行了系统仿真及分析,仿真结果表明自适应模糊PI控制的永磁同步电机系统调速性能优于传统的PI控制。自构模糊控制并加以切换策略计算反向传播得误差,有效地克服了参数突变和负载扰动,获得了永磁同步电机调速更理想的控制效果。
参考文献:
[1] 舒志兵. 交流伺服运动控制系统[M]. 北京: 清华大学出版社, 2006.
SHU Zhi-bing. AC servo motion control system[M]. Beijing: Tsinghua University Press, 2006.
[2] Shyu K K, Lai C K, Tsai Y W, et al. A newly robust controller design for position control of permanent-magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2002, 49(3): 558-565.
[3] 庄伟. 基于dsPIC的永磁同步电机矢量控制系统[D]. 大连: 大连理工大学, 2007.
ZHUANG Wei. Vector control system of PMSM based on dsPIC[D]. Dalian: Dalian University of Technology, 2007.
[4] 彭长华, 王友利, 沈艳霞, 等. 永磁同步电动机新型模糊PI控制器的设计[J]. 江南大学学报, 2008(3): 272-275.
PENG Chang-hua, WANG You-li, SHEN Yan-xia, et al. Design of novel fuzzy PI controller for PMSM drive system[J]. Journal of Jiangnan University, 2008(3): 272-275.
[5] Jung J W, Choi Y S, Leu V Q, et al. Fuzzy PI-type current controllers for permanent magnet synchronous motors[J]. IET Electric Power Applications, 2011, 5(1): 143-152.
[6] Lin C J, Chen C H. A self-constructing compensatory neural fuzzy system and its applications[J]. Mathematical and Computer Modeling, 2005, 42(3): 339-351.
(编辑 陈爱华)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:教育部新世纪优秀人才支持计划项目;辽宁省科技计划项目;大连市科技基金项目;国家自然科学基金资助项目(51079013)
通信作者:于双和(1968-),男,黑龙江巴彦人,教授,从事自动控制研究;电话:0411-84723025;E-mail: shuanghe@dlmu.edu.cn