J. Cent. South Univ. (2016) 23: 1799-1806

DOI: 10.1007/s11771-016-3233-7

Exploring relations between city regions based on mobile phone data

WANG Shuo-feng(汪烁枫)¹, LI Zhi-heng(李志恒)^{1, 2}, JIANG Shan(姜山)^{1, 2}, XIE Na(谢娜)³

1. Department of Automation, Tsinghua University, Beijing 100084, China;

2. Graduate School at Shenzhen, Tsinghua University, Shenzhen 518055, China;

3. School of Management Science and Engineering, Central University of Finance and Economics,Beijing 100081, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: City regions often have great diversity in form and function. To better understand the role of each region, the relations between city regions need to be carefully studied. In this work, the human mobility relations between regions of Shanghai based on mobile phone data is explored. By formulating the regions as nodes in a network and the commuting between each pair of regions as link weights, the distribution of nodes degree, and spatial structures of communities in this relation network are studied. Statistics show that regions locate in urban centers and traffic hubs have significantly larger degrees. Moreover, two kinds of spatial structures of communities are found. In most communities, nodes are spatially neighboring. However, in the communities that cover traffic hubs, nodes often locate along corridors.

Key words: mobile phone data; city relations; community; degree

1 Introduction

The development of a city usually leads to different functional regions. Understanding the relations between regions of a city is useful for city planner.

Researchers had studied various relations, such as human mobility, flows of commodity, and information communication. In this work, we focus on human mobility relations. As a transition of residents between regions, human mobility plays an important role in the spread of infectious diseases [1], the structure of social network [2], the detection of traffic anomalies [3], and traffic forecasting [4]. The strengths of relations between different regions can be represented by the daily flow volumes of human.

Most previous studies estimated the strengths of relations based on census dataset [5]. However, it takes lot of time and money to implement a census.

Recently, some researchers have attempted to study the strengths of relations based on location sensors data because those data are easily available. Many kinds of data are used to depict human mobility [6], such as media check-in data [7], mobile phone data [8] taxi trips data [9], and even social network data [10]. Among these data, mobile phone data have some advantages. First, almost every people can be monitored by mobile phone network because of the high mobile phone penetration rate. Second, almost at any time people can be monitored by mobile phone network because the mobile phones always work throughout the whole day.

Researchers had carried out several human mobility studies based on mobile phone data. For example, WHITE and WELLS [11] extracted origin destination information of human mobility data from mobile phone data. KANG et al [12] uncovered the relationship between human mobility and urban morphology based on mobile phone data.

In mobile phone data, cells are the minimum position units (please see Section 2 for details about the regions definition). In this work, we call a cell as a region and we focus on the relations between regions. Particularly, we depict the relations between regions via a network. The nodes in this network represent different regions, and the weighted edges represent the daily flow volumes between nodes.

Specially, we address two attributes of this network: distribution of nodes degree, and spatial structures of communities in networks, to characterize the relations between regions. Degree is the number of edges incident to the node [13]. Researchers find that degree is an indicator of a node’s importance in the network [14]. Community is a group of nodes which connect more densely to each other than to the rest of the weighted network [15]. Statistics show that regions locate in urban centers and traffic hubs have significantly larger degrees. In this work, traffic hubs are defined as important traffic infrastructures such as airport and railway station. Moreover, two kinds of spatial structures of communities are found. In most communities, nodes are spatially neighboring. However, in the communities that cover traffic hubs, nodes often locate along corridors. Corridors are defined as transportation mainlines, such as subway and expressway.

In this work, we firstly describe the study area Shanghai, China, the definition of regions, and the main features of the mobile phone data collected in Shanghai. Then, the spatial interaction network from the perspective of degree distribution and the spatial interaction network from the perspective of communities are studied.

2 Descriptions and preprocessing on empirical data

2.1 Study area and regions definition

Shanghai is the financial center of China. It is comprised of 16 districts and one county. Its urban area contains eight districts: Huangpu District, Xuhui District, Changning District, Jing’an District, Putuo District, Zhabei District, Hongkou District, and Yangpu District. The other districts are collectively called the suburbs (see Fig. 1). The studied area covers the whole area of Shanghai, which is about 6340.5 km².

Before defining the so called regions, let us briefly introduce the cellular network (see Fig. 2). In a cellular network, there are a lot of base stations. As for Shanghai, the cellular network consists of 40374 base stations. The signals from one or more mobile phones in an area (the cell in Fig. 2) are received by a base station. One location area consists of several adjacent base stations, equivalently several adjacent cells. Researchers have found that mobile phone chooses the closest base station to establish connection [16]. According to the connection mechanism, we can get the cell of each base station.

In this work, we get the cell of each base stations by the Voronoi diagram [17-18] which accords with the connection mechanism. The Voronoi diagram is defined as

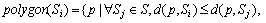
                            (1)

where polygon(S_i) is the cell of base station S_i, S is the set of all base stations, p is any point on the plane, d(x, y) is the distance between x and y. According to the definition, base station S_i is the closest base station to all points in the cell of base station S_i. Therefore, the definition of cell accords with the connection mechanism.

After getting the cell of each base station, we can give the definition of regions. One region is defined as the cell of a base station. Polygonal regions are shown in Fig. 3.

2.2 Extraction of human mobility flows and construction of relation network

The mobile phone data used in this work were collected by Shanghai China Mobile Communications Corporation (CMCC). All mobile phone data used are collected at 18 Oct, 2013, except where noted. The dataset covers millions of records for about 16 million phone users.

Each record in the data set contains the following information: User ID, Cell ID, LA ID, Event ID, and Event Time. The CMCC gives every users a unique User ID which is encrypted. One cell ID corresponds to one base station. LA ID corresponds to the location area (LA) which the base station belongs to. There are 143 location areas in Shanghai. Event ID corresponds to the event type such as making a call or sending a message. Event Time is the time when the event happens.

Fig. 1 An illustration of districts in Shanghai:

Fig. 2 A brief illustration of a cellular network

For each User ID, we collect all mobile phone communication records corresponding to the User ID, then we sort the records based on time. As the location information cell ID, LA ID have also been recorded incommunication records, we can get the mobility traces for each User ID. Finally, we transform the mobility traces to origin-destination (OD) flows. For example, if the mobility trace is A-B-C-D, we can get 3 OD records from the mobility trace: A-B, B-C and C-D.

Based on the OD records, we can build a spatial interaction network N_b, in which nodes represent cells, edges represent OD links and weights of the edge represent the total OD records quantity between the two cells. In other words, each node V_i corresponds to a cell S_i, and each edge E_ij corresponds to the total records quantity between the cell S_i and cell S_j. We omit OD records whose origin and destination are the same. As a result, there are only 34949 not 40374 nodes in network N_b.

Similarly, we can define another relation network: namely, LA-Network N_l. Weights of the edge in N_l represent the total OD records quantity between cells belonged to the two location area. The network N_l contains 143 nodes corresponding to the 143 location areas. Therefore, we have two kinds of relation networks in this paper: namely, Cell-Network N_b and LA-Network N_l. The relationship between N_b and N_l is shown in Fig. 4.

In Fig. 4(a), the network N_b contains 6 cells which belong to 3 different location areas. In Fig. 4(b), the network N_l contains 3 different location areas. The edges in network N_b represent OD records whose origin and destination belong to different cells. The edges in network N_l represent OD records whose origin and destination belong to different location areas.

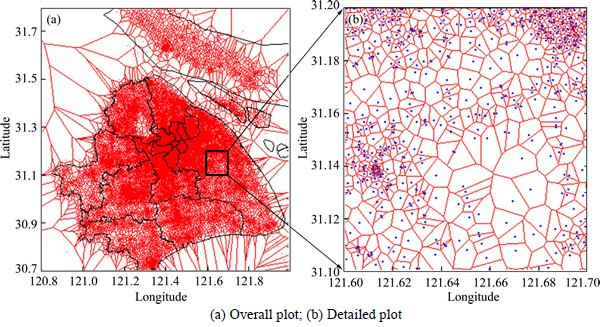
Fig. 3 Illustration of cells:

Fig. 4 Relationship between N_b and N_l:

3 Distribution of degree for relation networks

The observed total commuting amount in network N_b is 428794380 and the total edges weights in network N_l are 25357796.

The average degree of nodes in network N_l is 140, but the number of nodes in network N_l is 143. So, each node in network N_l almost connects with all the other nodes. As the degrees of each node in network N_l are almost the same, we only make an analysis on the nodes degree distribution in network N_b (see in Figs. 5 and 6).

Fig. 5 Frequency distribution of nodes’ degree in network N_b

The average degree of nodes in network N_b is 656, but the number of nodes in network N_b is 34949. So, each node in network N_b only connects with only 1.9% nodes on average. We find that nodes (regions) with large degrees locate in urban areas or traffic hubs (e.g. the Pudong International Airport). This is mainly because that the urban areas have shopping malls, government and companies which attract many residents from all the regions in the city. The busy traffic hubs play a role as bridges between different regions and thus also attract many residents from nearby regions. Figure 5 indicates that the degree distribution of network N_b does not strictly follow power law, but the heavy tail feature still exists.

When the degree is lower than 250, the frequency number is almost constant. When the degree is larger than 3000, the frequency number is too small (lower than 100). Therefore, we choose several thresholds between 250 and 3000 to show the spatial location pattern of regions with different degrees in Fig. 6. The regions with degree less than 250 almost locate all over the map. If we focus on the regions with degree more than 250 in suburb, we can find that those regions are along with transportation lines. It is clearly that the regions in suburb areas with degree more than 500 are highly related to transportation lines. With the threshold of nodes degree increasing, the areas converge to urban areas. It indicates that the urban areas are related to many regions. There are several regions with degree more than 2000 far away from city center. Those regions locate around traffic hubs. For example, the two nodes (regions) marked with black rectangles, one locates around the Pudong International Airport and the other one locates where expressway A2 and expressway A30 cross.

4 Community detection

4.1 Community detection method

As a useful tool in the analysis of large complex networks [19], community detection tries to find communities in the network. Nowadays, many community detection methods have been developed to detect community in weighted network, such as methods proposed by NEWMAN and GIRVAN [14], and the “Louvain method” [20]. To evaluate the result of community detection, NEWMAN [21] have defined the modularity Q which Q lies between -1 and 1:

        (2)

where E_ij represents the weight of the edge between node V_i and node V_j, is the total weights of the edges attached to node V_i, k_i is also called the degree of node V_i. C_i is the community which node V_i belongs to, and The function δ(u, v) is 1 if u=v, and 0 otherwise.

In fact, the modularity Q evaluates how much the density of links inside detected communities differs from the expected density of links in a random network with similar number of vertices and edges [22]. If modularity Q is larger, the partition is better.

In this work, we adopt the “Louvain method” [20] which regards the community detection problem as a maximization problem. The “Louvain method” is a greedy algorithm. For more detailed information about the “Louvain method”, please refer to Ref. [13]. LAMBIOTTE and PANZARASA [23] proved that the “Louvain method” is faster and better than the method by CLAUSET et al [24].

4.2 Community detection in cell-network

Based on the “Louvain method”, we successfully divide the Cell-Network N_b into 627 communities and the modularity Q reaches up to 0.8095. Every community contains 55 base stations on the average.

Fig. 6 Distribution of nodes’ degree in network N_b:

To get more information of communities, first, we define the center coordinate of a community C as where 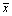and 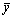means the mean value of nodes coordinates which belong to community C. Second, we define the “radius” r of a community as

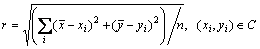    (3)

Figure 7 shows a community with 5 nodes and the “radius” r. In Fig. 7, the red nodes is the center of community and r₁, r₂, r₃, r₄, r₅ are the distances between the corresponding nodes and center. Then, the “radius” r is the root mean square (RMS) of r₁, r₂, r₃, r₄, r₅.

Fig. 7 Illustration of “radius”:

According to the definition, we can calculate the “radius” r of each community found above. The distribution of “radius” values is shown in Fig. 8. As Fig. 8 shows, there are 603 “radius” values of communities are smaller than 0.05. As each node’s coordinate in this paper is measured by the longitude and latitude of the corresponding base station, the value 0.05 approximately represent 5.5 km.

Based on the distribution of the “radius” values, we divide the total 627 communities into 2 classes according to whether their “radius” values are bigger than 0.05. There are two reasons why we take 0.05 as a reference. First, because 97% “radius” values of communities are smaller than 0.05. Second, the heavy tail feature becomes apparent in Fig. 8 when “radius” value is larger than 0.05.

The first class consisting of communities with “radius” values bigger than 0.05 is called the “bigger radius class”. The other class is called the “smaller radius class”.

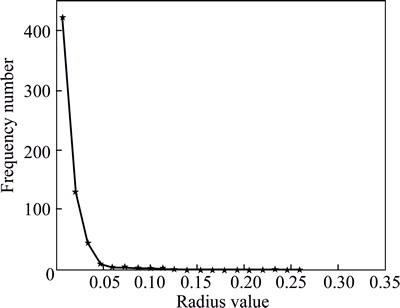
Fig. 8 Distribution of “radius” values

We find that the communities belonging to the “bigger radius class” usually have spatially spread structure (see in Fig. 9(a)), and they always cover traffic hubs. Their nodes (regions) locate along corridors. To verify this finding, we conduct a community detection based on mobile phone data collected from 16 Oct, 2013 to 22 Oct, 2013. We find the communities with spatially spread structure also locate along corridors (see in Fig. 9(b)). In Fig. 9(b), the community locates along subway line1 and subway 8. The communities belonging to the “smaller radius class” usually have spatially concentrated structure (see in Fig. 10). But for communities in the “smaller radius class”, there are also a few nodes which are far away from other nodes. Those nodes usually locate around traffic hubs such as subway stations.

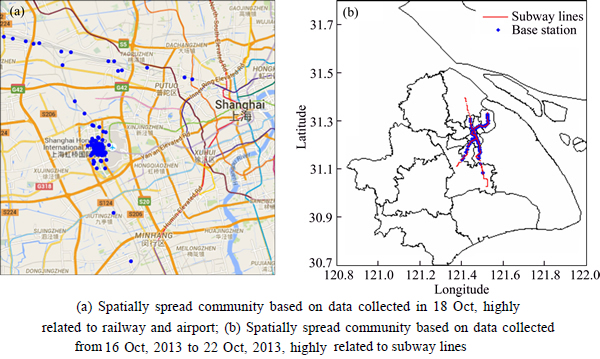
Fig. 9 Illustration of one spatially spread community:

Fig. 10 Illustration of one spatially concentrated community:

5 Conclusions

It is important for a city planner to understand the relations between regions of a city. As regions with close relations are more likely to suffer a series of coordinated terrorist attacks, understanding the relations between regions may be helpful to avoid the series of terrorist attacks. We explore the human mobility relations between the regions in Shanghai, based on mobile phone data. Formulating the regions as nodes in a network and the commuting between each pair of regions as link weights, we find that regions locate in urban centers and traffic hubs have significantly larger degrees. Moreover, in most communities, nodes are spatially neighboring; while in the communities that cover traffic hubs, nodes often locates along corridors.

References

[1] Belik V, Geisel T, Brockmann D. Natural human mobility patterns and spatial spread of infectious diseases [J]. Physical Review X, 2011, 1(1): 011001.

[2] Cho E, Myers S A, Leskovec J. Friendship and mobility: User movement in location-based social networks [C]// Proceedings of the 17th ACM SIGKDD International conference on Knowledge Discovery and Data mining. San Diego: ACM, 2011: 1082-1090.

[3] Pan B, Zheng Y, Wilkie D, Shahabi C. Crowd sensing of traffic anomalies based on human mobility and social media [C]// Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Orlando: ACM, 2013: 344-353.

[4] Liang Xiao, Zheng Xu-dong, Lv Wei-feng, Zhu Tong-yu. The scaling of human mobility by taxis is exponential [J]. Physica A: Statistical Mechanics and its Applications, 2012, 391(5): 2135-2144.

[5] Gao Song, Liu Yu, Wang Yao-li, Ma Xiu-jun. Discovering spatial interaction communities from mobile phone data [J]. Transactions in GIS, 2013, 17(3): 463-481.

[6] Liu Xi, Gong Li, Gong Yong-xi, Liu Yu. Revealing travel patterns and city structure with taxi trip data [J]. Journal of Transport Geography, 2015, 43: 78-90.

[7] Liu Yu, Sui Zheng-wei, Kang Chao-gui, Gao Yong. Uncovering patterns of inter-urban trip and spatial interaction from social media check-in data [J]. PloS one, 2014, 9(1): e86026.

[8] Kang Chao-gui, Sobolevsky S, Liu Yu, Ratti C. Exploring human movements in Singapore: A comparative analysis based on mobile phone and taxicab usages [C]// Proceedings of the 2nd ACM SIGKDD International Workshop on Urban Computing. Chicago: ACM, 2013: 1.

[9] Peng Cheng-bin, Jin Xiao-gang, Wong K C, Shi Me-xia, , P. Collective human mobility pattern from taxi trips in urban area [J]. PloS One, 2012, 7(4): e34487.

[10] Jurdak R, Zhao Kun, Liu Jia-jun, AbouJaoude M, Cameron M, Newth D. Understanding human mobility from Twitter [J]. PloS One, 2015, 10(7): e0131469.

[11] White J, Wells I. Extracting origin destination information from mobile phone data [C]// Eleventh International Conference on Road Transport Information and Control. London: IET, 2002: 30-34.

[12] Kang Chao-gui, Ma Xiu-jun, Tong Dao-qin, Liu Yu. Intra-urban human mobility patterns: An urban morphology perspective [J]. Physica A: Statistical Mechanics and its Applications, 2012, 391(4): 1702-1717.

[13] Newman M E J, Girvan M. Finding and evaluating community structure in networks [J]. Physical Review E, 2004, 69(2): 026113.

[14] Bagler G. Analysis of the airport network of India as a complex weighted network [J]. Physica A: Statistical Mechanics and its Applications, 2008, 387(12): 2972-2980.

[15] Papadopoulos S, Kompatsiaris Y, Vakali A, Spyridonos P. Community detection in social media [J]. Data Mining and Knowledge Discovery, 2012, 24(3): 515-554.

[16] Sevtsuk A, Ratti C. Does urban mobility have a daily routine? Learning from the aggregate data of mobile networks [J]. Journal of Urban Technology, 2010, 17(1): 41-60.

[17] Okabe A, Boots B, Sugihara K, Chiu, S N. Spatial tessellations: Concepts and applications of Voronoi diagrams [M]. New York: John Wiley & Sons, 2009.

[18] Wang Yan-wei, Li Zhi-heng, Li Li, Zhang Yi, Hu Jian-ming, Zhang Jia-jie, Guo Wei. Visualization analysis for urban human traveling behavior based on mobile phone data [C]// 15th COTA International Conference of Transportation Professionals. Beijing: CICTP, 2015: 1580-1591.

[19] Chen Yu, Xu Jun, Xu Min-zheng. Finding community structure in spatially constrained complex networks [J]. International Journal of Geographical Information Science, 2015, 29(6): 889-911.

[20] Blondel V D, Guillaume J L, Lambiotte R, Lefebvre E. Fast unfolding of communities in large networks [J]. Journal of Statistical Mechanics: Theory and Experiment, 2008(10): P10008.

[21] Newman M E J. Analysis of weighted networks [J]. Physical Review E, 2004, 70(5): 056131.

[22] Lou Xu-yang, Suykens J A K. Finding communities in weighted networks through synchronization [J]. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2011, 21(4): 043116.

[23] Lambiotte R, Panzarasa P. Communities, knowledge creation, and information diffusion [J]. Journal of Informetrics, 2009, 3(3): 180-190.

[24] Clauset A, Newman M E J, Moore C. Finding community structure in very large networks [J]. Physical Review E, 2004, 70(6): 066111.

(Edited by DENG Lü-xiang)

Foundation item: Project(71303269) supported by the National Natural Science Foundation of China; Project(14ZZD006) supported by the Economics Major Research Task of Fostering, China

Received date: 2015-09-20; Accepted date: 2016-03-01

Corresponding author: XIE Na, PhD; Tel: +86-13811306795; E-amil: xiena@cufe.edu.cn