DOI: 10.11817/j.issn.1672-7207.2016.10.034
全无缝化桥梁接线路面温升效应及端部位移计算
李嘉,赵乾文,邵旭东
(湖南大学 土木工程学院,湖南 长沙,410082)
摘要:为防止全无缝化桥梁体系对后续普通路面产生不利影响,开展无缝桥梁接线路面温升效应研究。建立温升状况下加筋接线路面计算模型,推导加筋接线路面受力、位移理论计算公式;通过分析锚固地梁结构受力变形机理,引入矩阵位移法,得到1~3道地梁端部位移与端部力的关系式。采用VB语言编制程序,计算接线路面板截面应力及其位移。研究结果表明:解析法所得接线路面板压应力与实桥监测压应力的相对误差为0.2%~14.4%,两者较接近,说明理论分析方法可用于全无缝化桥梁接线路面应力与位移计算;在最大温升情况下,路面板压应力小于材料抗压强度标准值;锚固地梁结构能有效控制端部位移。
关键词:道路工程;无缝桥梁;接线路面;受力分析;温度效应;锚固地梁
中图分类号:U416.22 文献标志码:A 文章编号:1672-7207(2016)10-3538-08
Research on temperature effect and anchor deformation for approach pavement of jointless bridge
LI Jia, ZHAO Qianwen, SHAO Xudong
(College of Civil Engineering, Hunan University, Changsha 410082, China)
Abstract: In order to prevent jointless bridge system from adverse impacts on the normal pavement, the temperature effect was studied for approach pavement behind the bridge abutment. Calculation model of the reinforced pavement slab was proposed, and the theoretical formulas for the slab stress and deformation was derived. After analyzing the mechanical mechanism of anchored ground beam structure, a matrix displacement method was introduced to obtain the relations between the anchor force and deformation at approach pavement end suiting to 1-3 ground beams. VB computer program was compiled to calculate the approach slab stress and deformation. The results show that the stress obtained by analytical method is in good agreement with that obtained by monitoring a test bridge. The relative errors is only 0.20%-14.37%, which shows that the theoretical analysis method is useful to calculate the slab stress and deformation of approach pavement for jointless bridge. Under the maximum temperature rise, the slab compressive stress is less than design compressive strength of approach pavement, and the anchor deformation can be controlled effectively by anchorage ground beam.
Key words: highway engineering; jointless bridge; approach pavement; mechanical analysis; temperature effect; anchorage ground beam
对于中小桥,温度变化产生的位移较小,因而可采用无缝化技术取消伸缩缝。自20世纪40年代以来,无缝桥梁使用越来越广泛[1] 。国内外学者对于整体式(半整体式)无缝桥梁开展了多项研究,如:DUNCAN等[2]将整体式桥台后土体或桩侧土体简化为弹簧作用,研究柔性桩基随梁体的温度变形而发生变形的规律,指出桩顶的水平变形量最大,桩内应力增大会降低竖向承载力;DICLELI[3]利用Pushover分析法研究了典型整体式桥台与砂土之间的相互关系,发现台后土压力的分布和压力与桥台高度相关,同时与桥台位移、桩的类型、桩侧砂的密度相关;AROCKIASAMY等[4]研究了温度、混凝土收缩徐变对整体式桥梁受力变形的影响;DICLELI[5]认为无缝桥梁设计应该根据施工阶段进行计算,不同的施工阶段考虑的荷载不同,其计算模型不同;DICLELI等[6]通过对H钢桩的性能、温度、桩-土共同作用、整体式桥台-土共同作用、桥台与桩联结构造等进行研究,提出了无缝桥梁在不同气候下的桥长限度。欧美等国的典型整体式或半整体式无缝桥梁是将伸缩缝由桥台处移至搭板末端,它虽然解决了桥梁伸缩缝的诸多问题,但搭板末端的接缝仍处于易损状态[7]。金晓勤等[8-10]在分析与研究无缝桥梁受力特性的基础上,利用连续配筋混凝土路面允许带裂缝工作的特点,提出了适应中、小桥梁的全无缝桥梁结构体系,即将主梁、搭板与接线路面及锚固地梁整体连接,主梁温度变形通过搭板传递给特殊设计的连续配筋接线路面及末端地梁。这种全无缝桥梁体系进一步取消了桥梁与路面衔接处的伸缩装置,运营维护费用更少,行车舒适性更高,且大幅度增强了抗震能力。全无缝桥梁主梁的温降变形通过专用的连续配筋接线路面吸纳[10],本文作者针对温升状况下接线路面的受力特性进行分析,进而推导接线路面板应力、位移解析解;利用得到的解析公式编程计算接线路面板应力及其端部位移,从而确定末端地梁设置道数的合理值。将解析法的计算结果与广西河口中桥的实测结果进行对比分析,验证解析法计算的可行性。
1 接线路面温升效应分析
全无缝桥梁接线路面采用特殊设计的带锯缝连续配筋混凝土路面[11-13]。在温度上升的情况下,主梁膨胀挤压搭板,并推动其后的接线路面板及锚固地梁,如图1所示。
1.1 计算模型
温度上升时,接线路面板受搭板推力、板底摩阻力及端部约束共同作用,受力模型如图2所示。
根据平衡条件,由图2可得单位宽度接线路面板的轴向推力:
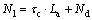 (1)
(1)
 (2)
(2)
式中:N1为搭板对路面板的轴向压力(kN);Ni(i=1,2,…,n)为第i段混凝土路面板的轴向压力(kN);La为接线路面总长度(m);L0为锯缝间距,取L0=1 m;τc为接线路面板底的摩阻应力(MPa);Nd为接线路面端部水平力(kN)。
1.2 基本假定
在温升条件下,对接线路面板进行受力分析时,基本假定如下:1) 混凝土应力沿截面均匀分布,温度沿着混凝土截面均匀变化;2) 路面板与隔离层之间的摩阻应力τc为τc=kc·uc(式中,kc为接线路面板与隔离层间的摩阻力系数(MPa/mm),kc=γl·μ·hc;hc为路面板厚度(m);γl为路面板计算容重(kN/m3);μ为路面板底摩阻系数);3) 钢筋与混凝土完全黏结,两者在x方向的位移相等,uc=us=u(x)[10]。
1.3 接线路面板受力分析
取任意长度x处的微元体dx进行受力分析,微元体单元如图3所示。设单元混凝土面积与弹性模量分别为Ac和Ec,钢筋直径、面积与模量分别为ds,As和Es。

图1 接线路面示意图
Fig. 1 Diagram of reinforced approach pavement

图2 温升时的接线路面板受力图
Fig. 2 Forces of reinforced approach pavement slabs when temperature increases

图3 路面微元体分析单元
Fig. 3 Unit analysis of pavement slab
图3中,水平方向平衡条件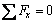 ,可得
,可得
 (3)
(3)
式中:σc为混凝土截面应力(MPa);σs为钢筋截面应力(MPa);d为纵向钢筋间距(m)。
又由 ,得
,得 。同理,
。同理, 。
。
uc和us分别为微单元混凝土和钢筋的位移变形量,且uc=us=u(x),代入式(3)可得
 (4)
(4)
式中:u(x)为微单元混凝土和钢筋的变形量;φ为钢筋贡献度,φ=p·n;p=As/Ac,为配筋率;n=Es/Ec,为弹性模量比。
求解微分方程(4),得到接线路面板混凝土和钢筋的位移为
 (5)
(5)
式中:c1和c2为待定系数;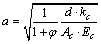 。
。
根据应力与位移的关系,在温升状况下,接线路面板混凝土与钢筋应力为:
 (6)
(6)
 (7)
(7)
式中:αc为混凝土线膨胀系数;αs为钢筋线膨胀系数。
在温升状况下,将接线路面板作为弹性整体进行受力分析。接线路面板左端受到来自主梁的压力N1作用,路面板底受到层间摩阻力τc作用,右端受到锚固地梁的约束力Nd作用,如图4所示。
根据图4,可以得到2个边界条件:
 ;
; (8)
(8)
式中:△lq为主梁(包括搭板)的膨胀变形。将式(8)代入式(5)中得到如下2个待定系数:
 ;
; (9)
(9)
将式(9)代入式(6)和(7),即可得到接线路面板混凝土和钢筋的应力解析解。

图4 温升下的接线路面变形示意图
Fig. 4 Deformation of slab when temperature increases
1.4 接线路面板端部位移
将式(9)代入式(5),可计算接线路面板端部位移ud:
 (10)
(10)
2 锚固地梁受力分析
在升温状况下, 为了避免无缝桥梁体系膨胀而挤压后续普通路面结构而产生的损害, 通常在接线路面端部设置1~3道锚固地梁,以约束端部位移。
2.1 锚固地梁受力机理
锚固地梁依靠其所承受的与位移方向相反的被动土压力来约束端部位移。锚固地梁构件及地梁之间土体简化模型如图5所示[14]。
当温度上升时,锚固地梁受到来自接线路面末端传递的推力Nd,使路面板和地梁结构向右移动,地梁发生扰动。此时,dc和ij面由静止土压力转变为被动土压力pp,土压力将增大;ab和gh面上的土压力由静止土压力转变为主动土压力pa,土压力将减小。土体dchg存在向右移动趋势,此时,土体dh面上产生向左的摩阻力。随着位移进一步增大,当地梁对侧土的作用大于pp-pa时,土体dchg可能会沿着de,dh和fh产生剪切破坏而开始整体滑动。

图5 锚固地梁结构模型
Fig. 5 Model of ground beam structure
2.2 锚固地梁水平位移计算
以2道地梁为例,锚固地梁的简化模型如图6所示[15]。

图6 锚固地梁的计算模型
Fig. 6 Calculation model of ground beam
计算基本假定如下。
1) 将混凝土视为线弹性材料,土基视为线弹性K地基。地基土对地梁的作用视为刚度为K的弹性支撑。其中地基参数K可由下式确定[16]:
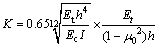 (11)
(11)
式中:K为地基反应系数(MPa/m);Et为地基弹性模量(MPa);Ec为混凝土基弹性模量(MPa);μ0为地基的泊松比,取0.35;I为锚固地梁惯性矩(m4),I=bh3/12;b为地梁宽度(m);h为地梁高度(m)。
2) 锚固地梁底部所受土体的摩阻力很小,可忽略不计。
3) 由于地梁相对较短,可将锚固地梁视为刚性桩,只产生平动和转动,本身挠曲变形忽略不计。
按照图6所示地梁计算模型,采用矩阵位移法计算锚固地梁端部水平位移ud:
 (12)
(12)
式中:m为设置地梁道数,在通常情况下,m=1,2,3;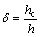 ;hc为接线路面板厚度(m);h为地梁高度(m);ld为地梁间距(m)。
;hc为接线路面板厚度(m);h为地梁高度(m);ld为地梁间距(m)。
3 接线路面应力与端部位移计算
在温升过程中,主梁膨胀,其变形通过搭板逐渐传递到路面以及地梁,通过路面板的弹性压缩以及地梁的变形来吸纳主梁温升变形量。
3.1 主梁及搭板温升变形量
假定温度中心在桥梁跨中,无缝桥梁主梁(包括搭板)产生的温升变形量△lq为
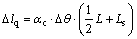 (13)
(13)
式中:αc为混凝土线膨胀系数;△θ为设计温差(℃);Ls为搭板长度。
3.2 接线路面板应力与端部位移计算
为方便计算,根据式(13),采用VB编制计算程序,可得到接线路面板截面应力及其位移,其计算流程见图7。
参照JTG D40—2011“公路水泥混凝土路面设计规范”,钢筋混凝土地梁梁宽b宜为0.4~0.6 m,梁高h宜为1.2~1.5 mm,地梁间距ld宜为5~6 m。
轴向压力搜索区间[N0,N2],取N0=τc·La,N2≤fc·Ac (其中,fc为混凝土抗压强度设计值,Ac为接线路面板横截面积)。
4 解析法计算结果与实测结果比较
广西百色市河口中桥是1座按全无缝桥梁结构体系设计的试验桥,桥梁全长80.0 m,两侧搭板各长 8.5 m,接线路面长度为30.0 m,接线路面端部锚固结构采用混凝土地梁,地梁高度为1.5 m,宽度为0.6 m。
4.1 解析法计算
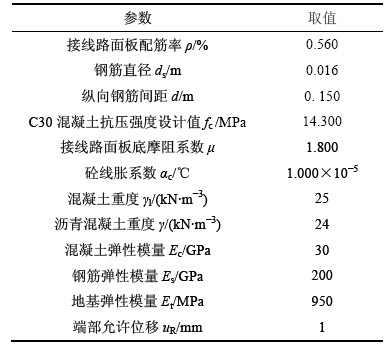
接线路面结构组合设计方案为:7 cm沥青混凝土面层+1 cm沥青封油层+24 cm C30连续配筋面层+土工布+2 cm沥青表处隔离层+10 cm C15水泥混凝土+25 cm水泥稳定碎石。接线路面基本计算参数见表1。
为了与实桥监测结果进行比较,利用接线路面应力及位移计算程序,分别计算年最大温升工况下,距0号台侧搭板27 m、距4号台侧搭板27.0 m和27.5 m处路面板应力。
4.2 监测结果
在河口桥施工过程中,在主梁、搭板及接线路面的关键部位预埋弦式混凝土应变计及压力盒。自2010-04通车以来,广西公路管理局对运营期间的试验桥进行了为期1年半的跟踪监测,即每隔半月测试路面温度、搭板及接线路面板混凝土应变等。在此期间,试验桥经历了当地的年最高温度与最低温度。在温升条件下,端部地梁结构处于最不利工作状况。本文将温升季度0号台侧距搭板27 m、4号台侧距搭板27 m和27. 5m处路面板应力监测结果见图8~10。

图7 接线路面板应力及位移计算流程
Fig. 7 Calculation flow of slab stress and deformation
表1 接线路面计算基本参数
Table 1 Parameters of approach pavement
4.3 解析法计算结果与监测结果对比
从图8可以看出:实测截面压应力随着温升幅度增加而增大,其变化规律与温度变化有较好的一致性;解析法计算值与实桥监测值较接近,实测值与理论值相对误差为0.2%~13.9%,且理论值稍大于实测值;在全年最大温差△θ为+18 ℃时,板内最大压应力为5.6 MPa,小于C30混凝土抗压强度标准值14.3 MPa。
图9和图10所示分别为4号台侧距搭板27 m和27.5 m处接线路面板应力实测值与理论计算值。从图9和图10可以看出:全年监测到最高温升幅度△θ为+20 ℃,实测最大压应力分别为6.53 MPa和6.32 MPa,表明在相同环境温度下, 越近搭板压应力越大,与式(2)所得结果相吻合;解析法计算值与实桥监测值较近,由图9和图10可以看出,4号台侧跨搭板27.0 m和27.5 m处接线路面板应力实测值与理论值相对误差分别为1.1%~14.4%和 0.4%~12.6%。对于实测值,板中应力和板边应力均与理论计算值差异较小,说明理论公式不仅适用于计算板中应力,而且可以计算板边应力,这与本文的受力分析模型所得结果一致。
4.4 端部应力与端部位移计算
考虑温升幅度为10,15,20,25和30 ℃这5种工况,计算接线路面端部应力与端部位移,如表2 所示。

图8 27 m处接线路面温度变化与截面应力(0号台侧)
Fig. 8 Actual temperature and stress variation at 27 m for No.0 station
表2 端部应力与端部位移计算结果
Table 2 Results of stress and deformation


图9 27 m处接线路面温度变化与截面应力(板中) (4号台侧)
Fig. 9 Temperature and stress variation at 27 m for No.4 station

图10 27.5 m处接线路面温度变化与截面应力(板边) (4号台侧)
Fig. 10 Temperature and stress variation at 27.5 m for No.4 station
从表2可知:随着温升幅度增加,端部应力、端部位移均随之增大;当温升幅度一定时,端部位移随地梁道数增加而明显减少。计算表明:当温升幅度不超过10 ℃时,桥梁产生的温度变形较小,其膨胀量主要由无缝桥体系自身弹性压缩吸收,不需要设置地梁即可满足设计要求(ud<1 mm);当温升幅度为10~20 ℃时,为保证端部位移控制在1 mm之内,需设置1道地梁;若温升幅度达20~30 ℃,则主梁膨胀位移较大,需要设置2道地梁才能满足端部位移ud<1 mm的设计要求。
5 结论
1) 基于全无缝桥梁接线路面板受力变形特点,建立了温升状况下加筋接线路面计算模型,推导了考虑锚固地梁影响的接线路面应力、位移解析公式。
2) 通过分析锚固地梁结构受力变形机理,采用矩阵位移法,得到1~3道地梁在水平推力作用下端部位移与端部力的关系式。
3) 根据解析公式并进行流程设计,编程计算接线路面板截面应力及其位移。
4) 接线路面板应力解析法计算结果与实桥监测结果较接近;板内最大压应力小于材料抗压强度标准值。
本文未考虑地基摩阻力非线性本构关系的影响。在后续研究中,需进一步针对设计参数开展敏感性分析与研究。
参考文献:
[1] MARURI R, PETRO S. Integral abutments and jointless bridges (IAJB) 2004 survey summary[C]//Baltimore&Maryland. Integral Abutment and Jointless Bridges(IAJB 2005). Federal Highway Administration, 2005: 12-29.
[2] DUNCAN J M, ARSOY S. Effect of bridge-soil interactions on behavior of piles supporting integral bridges[J]. Journal of the Transportation Research Board, 2003, 1849(11): 91-97.
[3] DICLELI M. Integral abutment-backfill behavior on sand soil-pushover analysis approach[J]. Bridge Engineering, 2005, 10(3): 354-364.
[4] AROCKIASAMY M, BUTRIENG N, SIVAKUMAR M. State-of-the-art of integral abutment bridges: design and practice[J]. Journal of Bridge Engineering, 2004, 9(5): 497-506.
[5] DICLELI M. Simplified model for computer-aided analysis of integral bridges[J]. Journal of Bridge Engineering, 2000, 5(3): 240-248.
[6] DICLELI M, ALBHAISI S M. Estimation of length limits for integral bridges built in clay[J]. Journal of Bridge Engineering, 2004, 9(6): 572-581.
[7] Alberta Transportation Bridge Structures Design Criteria. Appendix A: integral abutment design guidelines[S].
[8] 金晓勤, 邵旭东. 半整体式全无缝桥梁研究[J]. 土木工程学报, 2009, 42(9): 68-73.
JIN Xiaoqin, SHAO Xudong. A study of fully jointless bridge-approach system with sem-integral abutment[J]. China Civil Engineering Journal, 2009, 42(9): 68-73.
[9] 邵旭东, 占雪芳, 金晓勤, 等. 带地梁的新型半整体式无缝桥梁温度效应研究[J]. 中国公路学报, 2010, 23(1): 47-52.
SHAO Xudong, ZHAN Xuefang, JIN Xiaoqin, et al. Temperature effect of innovative semi-integral abutment jointless bridge with ground beam[J]. China Journal of Highway and Transport, 2010, 23(1): 47-52.
[10] ZHAO Yibin, SHAO Xudong, JIA Li, et al. Study on temperature effect of single expansion joint bridge[C]// International Association for Bridge and Structure Engineering. IABSE Congress Report 18th Congress of IABSE. Seoul, Korea, 2012: 1619-1626.
[11] 邵旭东, 陈志新, 金晓琴, 等. 无缝桥加筋接线路面的拉伸变形性[J]. 中国公路学报, 2010, 23(6): 34-40.
SHAO Xudong, CHEN Zhixin, JIN Xiaoqin, et al. Tensile deformation performance of reinforced approach pavement of jointless bridge[J]. China Journal of Highway and Transport, 2010, 23(6): 34-40.
[12] 占雪芳, 邵旭东. 半整体式无缝桥中带预压缝的配筋接线路面温降效应[J]. 土木工程学报, 2011, 11(1): 74-78.
ZHAN Xuefang, SHAO Xudong. Temperature effect of reinforced approach pavement of semi-integral abutment jointless bridge with precutting cracks for temperature drops[J]. China Civil Engineering Journal, 2011, 11(1): 74-78.
[13] 李嘉, 陈建中, 邵旭东. 全无缝化桥梁接线路面温降效应及长度优化[J]. 中国公路学报, 2015, 28(2): 53-59.
LI Jia, CHEN Jianzhong, SHAO Xudong. Temperature effect and length optimization for approach pavement of jointless bridge[J]. China Journal of Highway and Transport, 2015, 28(2): 53-59.
[14] 邓学钧, 陈荣生. 刚性路面设计[M]. 北京: 人民交通出版社, 2005: 432-435.
DENG Xuejun, CHEN Rongsheng. Rigid pavement design[M]. Beijing: China Communications Press, 2005: 432-435.
[15] 中国船舶工业总公司第九设计研究院. 弹性地基梁及矩形板计算[M]. 北京: 国防工业出版社, 1993: 37-39.
The Ninth Design & Research Institute. Beam and rectangular plate on elastic foundation calculation[M]. Beijing: National Defense Industrial Press, 1993: 37-39.
[16] 钟春玲, 刘寒冰, 孟广伟, 等. 连续配筋混凝土路面端部锚固解析解[J]. 土木工程学报, 2010, 43(10): 143-148.
ZHONG Chunling, LIU Hanbing, MENG Guangwei, et al. Analytical solution for anchored end of continuously reinforced concrete pavement[J]. China Civil Engineering Journal, 2010, 43(10): 143-148.
(编辑 陈灿华)
收稿日期:2015-10-13;修回日期:2015-12-02
基金项目(Foundation item):交通部西部交通建设科技项目(2009318000044);国家自然科学基金资助项目(51078135)(Project (2009318000044) supported by the Western Transportation Construction of Ministry of Transportation; Project (51078135) supported by the National Natural Science Foundation of China)
通信作者:李嘉,教授,从事路基路面新材料和新技术研究;E-mail:lijia@hnu.edu.cn