硅酸铝短纤维增强镁基复合材料的 蠕变机制及蠕变本构模型
来源期刊:中国有色金属学报(英文版)2014年第3期
论文作者:田 君 石子琼
文章页码:632 - 640
关键词:镁基复合材料;门槛应力;有效应力;本构模型
Key words:magnesium matrix composites; threshold stress; effective stress; constitutive model
摘 要:利用常应力拉伸蠕变实验法对体积分数为30%的硅酸铝短纤维增强AZ91D镁基复合材料及其基体合金AZ91D在不同温度和应力下进行蠕变测试。结果表明:2种材料的真应力指数均为3,真蠕变激活能均等于144.63 kJ/mol;复合材料的蠕变是由基体的蠕变控制,以位错黏滞性滑移控制为主,晶界滑移控制为辅。由实验数据获得的蠕变本构模型的经验公式能较好地描述复合材料的蠕变变形规律。
Abstract: By the constant stress tensile creep test method, creep tests were performed on aluminum silicate short fiber-reinforced AZ91D magnesium matrix composite with volume fraction of 30% and its matrix alloy AZ91D under different temperatures and stresses. The results indicate that the composite and the matrix have the same true stress exponent and true activation energy for creep, which are 3 and 144.63 kJ/mol, respectively. The creep of the composite is controlled by the creep of its matrix, which is mainly the controlling of viscous slip of dislocation, and the controlling of grain boundary slippage as a supplement. The creep constitutive model obtained from the experiment data can well describe the creep deformation pattern of the composite.
Trans. Nonferrous Met. Soc. China 24(2014) 632-640
Jun TIAN, Zi-qiong SHI
School of Mechanical Engineering, Dongguan University of Technology, Dongguan 523808, China
Received 7 February 2013; accepted 3 July 2013
Abstract: By the constant stress tensile creep test method, creep tests were performed on aluminum silicate short fiber-reinforced AZ91D magnesium matrix composite with volume fraction of 30% and its matrix alloy AZ91D under different temperatures and stresses. The results indicate that the composite and the matrix have the same true stress exponent and true activation energy for creep, which are 3 and 144.63 kJ/mol, respectively. The creep of the composite is controlled by the creep of its matrix, which is mainly the controlling of viscous slip of dislocation, and the controlling of grain boundary slippage as a supplement. The creep constitutive model obtained from the experiment data can well describe the creep deformation pattern of the composite.
Key words: magnesium matrix composites; threshold stress; effective stress; constitutive model
1 Introduction
The great importance placed on light materials by the automobile, aerospace, and electronic industries necessarily introduces magnesium alloy as a promising candidate for extensive use in these fields [1-4]. AZ91 is the most commonly used magnesium alloy due to its good property profile, but suffers from its poor creep behaviour at elevated temperatures, especially under long-term loading conditions, and is restricted at temperatures above 423 K [5-7]. An effective way to improve the creep properties of alloys is to add reinforcement to alloys forming composites [8-11]. Recent tests have confirmed that the AZ91D magnesium matrix composite, which is fabricated by the squeeze-casting method with aluminum silicate short fibers as reinforcement, has a good bonding interface, and could enhance the composite significantly [12]. Several studies have been conducted in the high temperature creep of short fiber reinforced metal matrix composites. For example, the assessment of back-stress and load transfer approaches for rationalizing creep of short fiber reinforced aluminum alloys has been demonstrated [13].  et al [14] studied creep properties and behaviors of an unreinforced AZ91 magnesium alloy and a similar alloy reinforced with short alumina fibers, and the results showed that the introduction of short alumina fibers into an AZ91 magnesium alloy improved the creep resistance due to the introduction of a threshold stress that served to reduce the effective stress acting on the material.
et al [14] studied creep properties and behaviors of an unreinforced AZ91 magnesium alloy and a similar alloy reinforced with short alumina fibers, and the results showed that the introduction of short alumina fibers into an AZ91 magnesium alloy improved the creep resistance due to the introduction of a threshold stress that served to reduce the effective stress acting on the material.  et al [15] conducted creep tests on an AZ91-20%Al2O3 (volume fraction) short fiber composite and on an unreinforced AZ91 matrix alloy, and the results showed that the creep resistance of the reinforced material improved considerably compared with the matrix alloy; the creep-strengthening arose primarily from the effective load transfer between plastic flow in the matrix and the fibers. OLBRICHT et al [16] studied mechanical and microstructural observations during compression creep of a short fiber reinforced Al-Mg metal matrix composite, and it was concluded the orientation of Al2O3fibers with respect to the loading axis affected minimum creep rates, and fiber breakage represented an important damage mechanism. SPIGARELLI and MEHTEDI [17] investigated microstructure-related equations for the constitutive analysis of creep in magnesium alloys, and a new model, developed by relating a modified form of the Garofalo’s which was equation and the concentration of aluminum in a solid solution, had been used to describe the minimum creep rate dependence of applied stress and temperature. Although the creep behavior of short fiber reinforced metal matrix composites and the creep constitutive relation of metal alloys were studied, the creep constitutive relation of short fiber reinforced metal matrix composites was not studied.
et al [15] conducted creep tests on an AZ91-20%Al2O3 (volume fraction) short fiber composite and on an unreinforced AZ91 matrix alloy, and the results showed that the creep resistance of the reinforced material improved considerably compared with the matrix alloy; the creep-strengthening arose primarily from the effective load transfer between plastic flow in the matrix and the fibers. OLBRICHT et al [16] studied mechanical and microstructural observations during compression creep of a short fiber reinforced Al-Mg metal matrix composite, and it was concluded the orientation of Al2O3fibers with respect to the loading axis affected minimum creep rates, and fiber breakage represented an important damage mechanism. SPIGARELLI and MEHTEDI [17] investigated microstructure-related equations for the constitutive analysis of creep in magnesium alloys, and a new model, developed by relating a modified form of the Garofalo’s which was equation and the concentration of aluminum in a solid solution, had been used to describe the minimum creep rate dependence of applied stress and temperature. Although the creep behavior of short fiber reinforced metal matrix composites and the creep constitutive relation of metal alloys were studied, the creep constitutive relation of short fiber reinforced metal matrix composites was not studied.
In order to ensure the safe use of the composite at high temperatures, it is an urgent matter to study the creep properties of the material, and in particular to obtain the model which precisely describes the constitutive relations between the creep parameters during the creep deformation process.
This study performed an investigation into the creep behavior of the aluminum silicate short-fiber-reinforced AZ91D composite by the constant stress tensile creep test method under different temperatures and stresses. Based on the creep test data and the electronic test, the creep mechanisms of the composite and its matrix as well as the load transfer mechanism of short fiber were analyzed. Subsequently, a high-temperature creep constitutive model of the composite was established, with the purpose of using these findings to guide the practical application of this material and enrich the theoretical creep studies of short-fiber-reinforced magnesium matrix composites.
2 Experimental
Aluminum silicate short-fiber-reinforced AZ91D composite was fabricated by the squeeze-casting method from aluminum silicate short fiber and AZ91D magnesium alloy (Mg-9%Al-1%Zn-0.3%Mn (mass fraction)). The aluminum silicate short fiber preform was formed by aluminum silicate short fibers (Al2O3-SiO2, ~5 μm in diameter with varying lengths up to ~80 μm) in random distribution, and the volume fraction of short fibers in the squeeze cast composite is about 30%. For convenient expression, hereinafter the aluminum silicate short-fiber-reinforced AZ91D composite with 30% short-fiber (volume fraction) was written as 30%Al2O3- SiO2(sf)/AZ91D or referred to as the composite, and the AZ91D magnesium alloy is referred to as the matrix alloy or the matrix for short. The composite and matrix alloy were performed tensile creep tests up to the final creep facture on the GWT105 durable testing machine under temperatures of 473, 523 and 573 K, and with applied stresses of 30-100 MPa. The test sample is shown in Fig. 1.
3 Results and discussion
3.1 Analysis of high-temperature creep curves
The strain-time curves of the matrix and the composite under different temperatures and loads are shown in Figs. 2 and 3. It can be seen that under thesame temperature, the composite bears more external stress than the matrix alloy, its steady-state creep time is about 10 times that of the matrix, and its creep curves are more moderate than the curves of the matrix, indicating that the composite has much stronger creep-resistant capacity than the matrix. When the stress is equal to or below a given value at a given temperature, the specimens will not creep, and the strain-time curve shows a flat line, suggesting that creep threshold stress may exist for both materials.

Fig. 1 Creep testing sample (unit: mm)

Fig. 2 Creep curves of AZ91 magnesium alloy under different stresses and temperatures

Fig. 3 Creep curves of 30%Al2O3-SiO2(sf)/AZ91D composite under different stresses and temperatures
3.2 Determination of creep apparent stress exponent
While the steady-state creep rate  is determined by the properties of the material itself, it is also the function of the temperature T and the stress σ. When the value of temperature T is fixed, under high temperature and low stress, lg
is determined by the properties of the material itself, it is also the function of the temperature T and the stress σ. When the value of temperature T is fixed, under high temperature and low stress, lg and lg σ of most materials have a linear relationship as follows [18-20]:
and lg σ of most materials have a linear relationship as follows [18-20]:
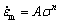 (1)
(1)
where A is the constant related to the material and temperature; n is the apparent stress exponent of the steady-state creep rate. The double logarithmic relationships of the steady-state creep rate  and stress σ are shown in Fig. 4. It can be derived from the figure that the maximum apparent stress exponents of the AZ91D matrix and the 30%Al2O3-SiO2(sf)/AZ91D composite are n=8.3 and n=22, respectively. References [6,18] considered that if a metallic material had a larger apparent stress exponent, the creep threshold stress for this metal material may exist, therefore the two materials may both have creep threshold stress.
and stress σ are shown in Fig. 4. It can be derived from the figure that the maximum apparent stress exponents of the AZ91D matrix and the 30%Al2O3-SiO2(sf)/AZ91D composite are n=8.3 and n=22, respectively. References [6,18] considered that if a metallic material had a larger apparent stress exponent, the creep threshold stress for this metal material may exist, therefore the two materials may both have creep threshold stress.
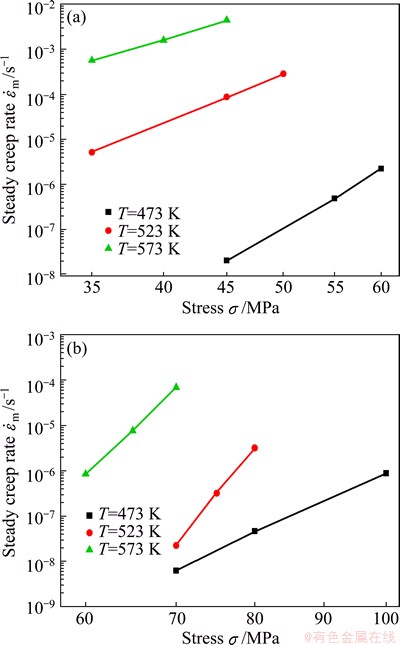
Fig. 4 Double logarithmic relationship of steady-state creep rate and stress for AZ91D alloy (a), 30%Al2O3-SiO2(sf)/AZ91D composite (b)
3.3 Determination of creep threshold stress and true stress exponent
If a creep threshold stress σth exists for a metallic material, then when the temperature is fixed, the steady-state creep rate equation can be expressed as follows [18,21]:
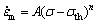 (2)
(2)
Equation (2) may be adapted to the equation as follows:
 (3)
(3)
where A is the constant related to the material and the temperature; n is the true stress exponent; σ is the applied stress; σth is the threshold stress.
By drawing a double-logarithmic relationship diagram of the steady-state creep rate  and the stress σ, the stress exponent obtained is smaller than the apparent stress exponent above, and this smaller stress exponent is called the true stress exponent. The matrix alloy of the Al2O3-SiO2(sf)/AZ91D composite is AZ91, and AZ91 is a solid solution alloy, which has smaller stress exponent at steady-state creep. The values 3 and 5 of the stress exponent stand for two important creep types of solid solution alloys. When n≤3, the stress exponent has a typical value of 3, this signifies that the creep behavior is very different from that of pure metal, which is called the first class of alloy-type creep; when n=4-7, its typical value is 5, which indicates that the creep behavior is similar to that of pure metals, and is called the second pure metal creep; when n≥8, the steady-state creep behavior can no longer be described by power-law equations [18,22].
and the stress σ, the stress exponent obtained is smaller than the apparent stress exponent above, and this smaller stress exponent is called the true stress exponent. The matrix alloy of the Al2O3-SiO2(sf)/AZ91D composite is AZ91, and AZ91 is a solid solution alloy, which has smaller stress exponent at steady-state creep. The values 3 and 5 of the stress exponent stand for two important creep types of solid solution alloys. When n≤3, the stress exponent has a typical value of 3, this signifies that the creep behavior is very different from that of pure metal, which is called the first class of alloy-type creep; when n=4-7, its typical value is 5, which indicates that the creep behavior is similar to that of pure metals, and is called the second pure metal creep; when n≥8, the steady-state creep behavior can no longer be described by power-law equations [18,22].
When  =0 and σ=σth, a straight line could be obtained by plotting
=0 and σ=σth, a straight line could be obtained by plotting 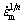 versus σ; the intercept of the straight line at the stress axis is the threshold stress. For the AZ91D matrix and the composite, the relationship diagrams of
versus σ; the intercept of the straight line at the stress axis is the threshold stress. For the AZ91D matrix and the composite, the relationship diagrams of 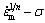 for n=3, 5 and 8 are plotted respectively. The figure with a more optimal linear relationship is chosen, the corresponding value of n is the true stress exponent; meanwhile the true threshold stress values at different temperatures could be obtained from the diagram.
for n=3, 5 and 8 are plotted respectively. The figure with a more optimal linear relationship is chosen, the corresponding value of n is the true stress exponent; meanwhile the true threshold stress values at different temperatures could be obtained from the diagram.
For the AZ91D matrix, the figure with the optimal linear relationship corresponds to n=3, as shown in Fig. 5(a). This result consists with the stress exponent n=3 that  et al [14] obtained by acoustic emission method to study the creep behavior of AZ91 alloy; some other Refs. [22,23] also studied the creep stress exponent n=3 of AZ91 alloy under low stress situation. The threshold stress value of the matrix can be obtained from the figure, as listed in Table 1.
et al [14] obtained by acoustic emission method to study the creep behavior of AZ91 alloy; some other Refs. [22,23] also studied the creep stress exponent n=3 of AZ91 alloy under low stress situation. The threshold stress value of the matrix can be obtained from the figure, as listed in Table 1.  et al [14] used acoustic emission method and found that at the temperature T=473 K, AZ91D alloy had acoustic emission response when the stress reached 40 MPa, which means the creep stress threshold of AZ91D alloy at this temperature was 40 MPa. This further proved the rationality of the test result of this study.
et al [14] used acoustic emission method and found that at the temperature T=473 K, AZ91D alloy had acoustic emission response when the stress reached 40 MPa, which means the creep stress threshold of AZ91D alloy at this temperature was 40 MPa. This further proved the rationality of the test result of this study.
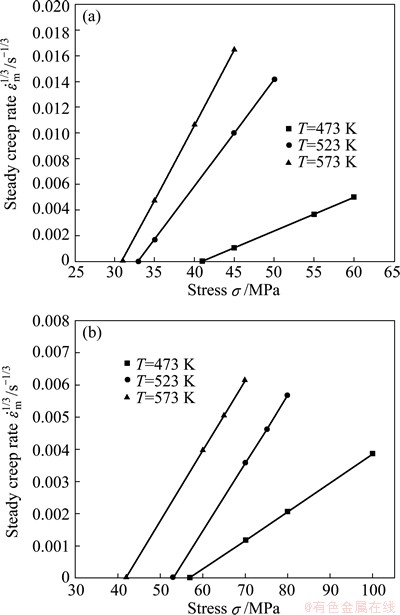
Fig. 5  plots for AZ91D alloy (a) and 30%Al2O3- SiO2(sf)/AZ91D composite (b)
plots for AZ91D alloy (a) and 30%Al2O3- SiO2(sf)/AZ91D composite (b)
Table 1 Creep threshold stress values of AZ91D magnesium alloy and Al2O3-SiO2(sf)/AZ91D composite

For the composite, when n=3, the figure has the best linear relationship, as shown in Fig. 5(b). From the figure, its threshold stress value could be obtained, as listed in Table 1. Apparently, the creep threshold stresses of the AZ91D alloy and the Al2O3-SiO2(sf)/AZ91D composite both decrease with the increase of the temperature.
3.4 Load transfer factor and creep effective stress of composite
It may be observed from Fig. 3(a) that when T=473 K and σ=70 MPa, the strain curve of the 30% Al2O3-SiO2(sf)/AZ91D composite is relatively flat, which means that its creep rate is smaller; and the threshold stress of the composite σthis 57 MPa, the difference between the external stress and the threshold stress is 13 MPa. As shown in Fig. 2(a), when T=473 K and σ=60 MPa, the strain curve of the alloy is quite steep, which means that its creep rate is large; while its threshold stress σth is 41 MPa, the difference between the external stress and the threshold stress is 19 MPa. After their respective threshold stresses are excluded, the external stress of the matrix and the composite are similar; however, their creep rates show large difference, the creep rate of AZ91D alloy is much larger than that of the composite, indicating that there are other factors acting on the creep of the composite. It is considered that the aluminum silicate short fiber reinforcement plays an effective role of bearing and load transference; it thus slows down the creep rate of the composite, and improves the creep resistance of the composite. Since the length of the short fibers varies, and the fibers have approximate two-dimensional random distribution, it is a highly complex problem to strictly handle the load transference mechanically. As a simplified empirical method, a load transfer factor α could be introduced when its value varies in the range of 0-1. When α=0, it indicates that there is absolutely no load transfer; while α=1, it indicates that all the loads are transferred to the short fibers. Assuming that load transfer only occurs when the external stress exceeds the threshold stress and causes creep deformation, the effective stress σe could be expressed by
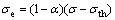 (4)
(4)
If assuming load transfer occurs when there is load, which means load transfer occurs in the stretch range, then the effective stress is expressed by
 (5)
(5)
Experiments proved that Eq. (4) is more realistic for expressing the effective stress. The empirical formula of the creep rate of the composite could be expressed as follows [18]:
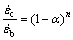 (6)
(6)
where  is the creep rate of the composite;
is the creep rate of the composite;  is the creep rate of the matrix; and n is the true stress exponent.
is the creep rate of the matrix; and n is the true stress exponent.
When creep occurs, temperature and stress are the two major external factors affecting the load transferring. In order to investigate the relationship between the load transfer factor α and the temperature and stress, the vary pattern of the load transfer factor with temperature and stress could be obtained by the obtained creep rates of the matrix and the composite. By calculating the value of α under different temperatures and stresses according to Eq. (6), the relationship diagram of the load transfer factor with the temperature and stress is plotted, as shown in Fig. 6. It can be seen that α is affected more by temperature than that by stress. This means that α depends mainly on temperature. To fit these space point with quadric surface equation, the empirical formula of α with temperature and stress is expressed as follows:

 (7)
(7)
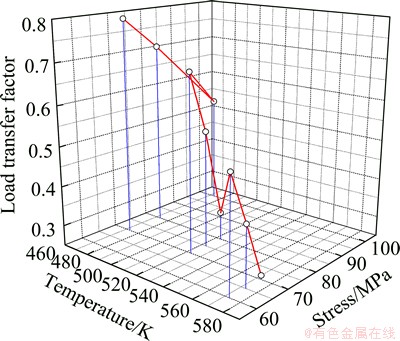
Fig. 6 Ralationship of load transfer factor with temperature and stress for 30%Al2O3-SiO2(sf)/AZ91D composite
The effective stress of the Al2O3-SiO2(sf)/AZ91D composite could be calculated by Eqs. (4) and (7).
As it may be observed, the effective stress is a comprehensive reflection of the impact of the creep threshold stress and the load transfer. The smaller effective stress is, the stronger creep resistance of the material is. Under the same conditions, the effective stress of the composite calculated by Eq. (4) is generally 0.1 to 0.5 times of the matrix, and the creep resistance of the Al2O3-SiO2/AZ91D composite is much greater than that of the matrix.
3.5 Determination of creep activation energy
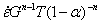 Figure 7 shows the logarithm of
Figure 7 shows the logarithm of  with the reciprocal of the thermodynamic temperature T. The true creep activation energy, which is the absolute value of the product of the straight line gradient and the gas constant, could be obtained [13]. The true creep activation energies of the two materials are the same, Q*c=144.63 kJ/mol. The diffusion activation energy of Al in Mg-Al alloy is 143 kJ/mol [18,24] which is close with the obtained true creep activation energy of the Al2O3-SiO2(sf)/AZ91D composite.
with the reciprocal of the thermodynamic temperature T. The true creep activation energy, which is the absolute value of the product of the straight line gradient and the gas constant, could be obtained [13]. The true creep activation energies of the two materials are the same, Q*c=144.63 kJ/mol. The diffusion activation energy of Al in Mg-Al alloy is 143 kJ/mol [18,24] which is close with the obtained true creep activation energy of the Al2O3-SiO2(sf)/AZ91D composite.
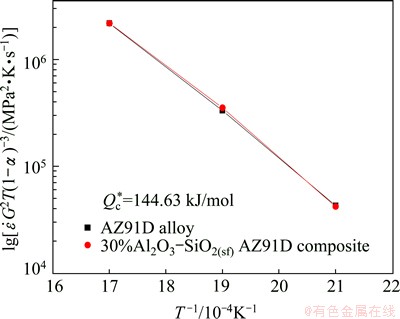
Fig. 7 1/T dependence of logarithm of  for AZ91D alloy and 30%Al2O3-SiO2(sf)/AZ91D composite
for AZ91D alloy and 30%Al2O3-SiO2(sf)/AZ91D composite
3.6 Analysis of creep mechanism of composite
From the analysis, the true stress exponents of the AZ91D magnesium alloy and the Al2O3-SiO2(sf)/AZ91D composite are the same, i.e. n=3; the true creep activation energy of the two materials are also the same, i.e. Q*c =144.63 kJ/mol, which is close with the diffusion activation energy 143 kJ/mol of Al in Mg-Al alloys. The creep threshold stresses of the two materials under the same temperature show little difference, and the basic properties of these creeps are the same, especially their true stress exponents are the same and their creep behaviors are similar, and furthermore, indicating that their creep mechanisms are the same, which means the creep of composite is controlled by the creep of the matrix.
The main feature of the first class of alloy type creep is that the stress exponent of the steady-state creep rate n=3 and the true creep activation energy is equal to the diffusion activation energy of solid solution. Thus, the creep mechanism of the AZ91D matrix is the same as the creep mechanism of the first class of solid solution alloy with stress exponent n=3, i.e. the creep rate is mainly controlled by the viscous slip of dislocation. The creep of both the AZ91D matrix alloy and the Al2O3- SiO2(sf)/AZ91D composite is controlled by dislocation; however, the steady-state creep rates of them under the same conditions are very different. The steady-state creep rate of the AZ91D matrix is far greater than that of the Al2O3-SiO2(sf)/AZ91D composite, indicating that the degrees of their creep controlled by dislocation are different. The dislocation of the AZ91D matrix is mainly affected by the dragging of the Al atomic solute atmosphere, while the dislocation of the composite is affected by not only the dragging of the Al atomic solute atmosphere, but also the dragging caused by the inconsistent deformations of the short fibers and the matrix, and thus the dislocation migration rate decreases. The existence of the short fibers hinders the migration of the dislocation, reduces the creep deformation degree, and improves the creep resistance.
Figures 8 and 9 show the fracture SEM morphologies of the creep fracture, the fractures of the AZ91D matrix alloy and the Al2O3-SiO2/AZ91D composite are dimple pattern with steps and holes generated on the fracture surface, indicating the existence of grain boundary migration and slippage [18,25].

Fig. 8 SEM image showing creep fractography of AZ91D matrix at T=523 K, σ=45 MPa

Fig. 9 SEM image showing creep fractography of Al2O3- SiO2(sf)/AZ91D composites at T=473 K, σ=100 MPa
3.7 Determination of constitutive model of creep parameters
Under the situation of high temperature and low stress, the constitutive model of the steady-state creep rate, the creep temperature and the applied stress of the metal alloy and its composite could generally be expressed by [18,22]
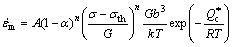 (8)
(8)
where  is the steady-state creep rate s-1; σ is the applied stress (MPa); σth is the true threshold stress (MPa); n is the true stress exponent;
is the steady-state creep rate s-1; σ is the applied stress (MPa); σth is the true threshold stress (MPa); n is the true stress exponent;  is the true creep activation energy (J/mol); T is the thermodynamic temperature (K); G is the shearing elastic modulus (the shearing elastic modulus of Mg is 1.92×104-8.6T) [18]; k is the Boltzmann constant (k=1.3806505×10-23 J/K); R is the gas constant (R=8.314 J·mol-1·K-1); b is the Burgers vector (b=3.2×10-10 m); A is the material constant; α is the load transfer factor of composite (the value of α for metal alloys is 0). The load transfer factor value of the Al2O3-SiO2(sf)/AZ91D composite is determined by Eq. (7).
is the true creep activation energy (J/mol); T is the thermodynamic temperature (K); G is the shearing elastic modulus (the shearing elastic modulus of Mg is 1.92×104-8.6T) [18]; k is the Boltzmann constant (k=1.3806505×10-23 J/K); R is the gas constant (R=8.314 J·mol-1·K-1); b is the Burgers vector (b=3.2×10-10 m); A is the material constant; α is the load transfer factor of composite (the value of α for metal alloys is 0). The load transfer factor value of the Al2O3-SiO2(sf)/AZ91D composite is determined by Eq. (7).
The creep experiment data of the AZ91D alloy and its composite are substituted in Eqs. (7) and (8), their material constant can be calculated as 1.12×1024and 8.86×1022, respectively.
The creep constitutive model of the AZ91D alloy is expressed as follows:
 (9)
(9)
The creep constitutive model of the 30%Al2O3- SiO2/AZ91D composite is expressed by
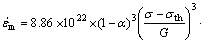
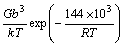 (10)
(10)
3.8 Comparative analysis of creep experiment data fitting result and creep constitutive model calculating result
Based on Eqs. (9) and (10), theoretical curves and the experimental curves of the steady-state creep stress of the AZ91D matrix and its composite are plotted using software programmed with the VB language, as shown in Fig. 10. It may be observed that the shapes and variation trends of the creep stress theoretical curves and experimental curves of two material are essentially the same, with minor deviations. This means the empirical formulas of the steady-state creep constitutive models of the AZ91D matrix and its composite obtained through experimental data are reasonable, and could represent a more preferable method of describing the creep deformation pattern of the AZ91D matrix and its composite. Meanwhile the degree of variance of the steady-state creep rate of Al2O3-SiO2(sf)/AZ91D composite with temperature and stress is far less than that of the AZ91D matrix, indicating that the composite has much stronger creep resistance ability than the matrix, mainly due to the greater creep threshold stress of the composite and the effective load transference. Analysis of the influencing factors of the creep constitutive models of two material shows that besides the temperature T, the stress σ and the threshold stress σth, there is also a load transfer factor α for the composite; the factor varies with temperature and stress, therefore it decides the great difference between the creep deformation patterns of the composite and the matrix. Obviously, the short fibers change the creep deformation pattern significantly.

Fig. 10 Experimental and theoretical curves of steady-state creep stress at T=473 K for AZ91D alloy at σ=45 Mpa (a), and 30%Al2O3-SiO2(sf)/AZ91D composite at σ=70 MPa (b)
4 Conclusions
1) The function of the short fibers in the composite could be described by the load transfer factor. At different temperatures and loads, the trend that the factor value reduces with the increase of the temperature is larger than that it reduces with the increase of the stress; the varying pattern of the factor could be described by empirical formula:
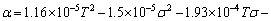

2) The high-temperature creep mechanisms of the Al2O3-SiO2(sf)/AZ91D composite and its matrix are the same. The creep of the composite is controlled by the creep of its matrix, which is the primary controller of the viscous slip of dislocation, and is the controller of grain boundary slippage as a side-benefit. The short fibers could hinder the migration of dislocations, reduce the creep rate, and improve creep resistance of the composite.
3) The creep constitutive model of the Al2O3-SiO2(sf)/AZ91D composite is
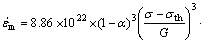
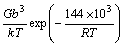 .
.
References
[1] Polmear I J. Magnesium alloys and applications [J]. Materials Science and Technology, 1994, 10(1): 1-16.
[2] AGHION E, BRONFIN B. Magnesium alloys development towards the 21stCentury [J]. Materials Science Forum, 2000, 350-351: 19-30.
[3] Spigarelli S, Mehtedi M E, Cabibbo M, Evangelistaa E. Analysis of high-temperature deformation and microstructure of an AZ31 magnesium alloy [J]. Materials Science and Engineering A, 2007, 462(1-2): 197-201.
[4] QIAO J, WANG Y, SHI G D. High temperature tensile behaviors of extruded and rolled AZ31 Mg alloy [J].Transactions of Nonferrous Metals Society of China, 2010, 20(2): 540-544.
[5] Srinivasan A, Swaminathan J, Gunjan M K, Pillaiaet U T S. Effect of intermetallic phases on the creep behavior of AZ91 magnesium alloy [J]. Materials Science and Engineering A, 2010, 527(6): 1395-1403.
[6] Pekguleryuz M, Celikin M. Creep resistance in magnesium alloys [J]. International Materials Reviews, 2010, 55(4): 197-217.
[7] TONG G D, LIU H F, LIU Y H. Effect of rare earth additions on microstructure and mechanical properties of AZ91 magnesium alloys [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(2): 336-340.
[8]  Deformation behaviour of an AS21 alloy reinforced by short Saffil fibres and SiC particles [J]. Journal of Materials Processing Technology, 2005, 162-163: 131-138.
Deformation behaviour of an AS21 alloy reinforced by short Saffil fibres and SiC particles [J]. Journal of Materials Processing Technology, 2005, 162-163: 131-138.
[9] Dragone T L, Nix W D. Steady state and transient creep properties of an aluminum alloy reinforced with alumina fibers [J]. Acta Metallurgicaet Materialia, 1992, 40(10): 2781-2791.
[10] Pandey A B, Mishra R S, Mahajan Y R. Steady state creep behaviour of silicon carbide particulate reinforced aluminium composites [J]. Acta Metallurgicaet Materialia, 1992, 40(8): 2045-2052.
[11] Pahutova M, Brezina J, Kucharova K,  a V. Metallographic investigation of reinforcement damage in creep of an AZ 91 matrix composite [J]. Materials Letters, 1999, 39(3): 179-183.
a V. Metallographic investigation of reinforcement damage in creep of an AZ 91 matrix composite [J]. Materials Letters, 1999, 39(3): 179-183.
[12] Tian J, Li W F, Han L F, Pen J H. Microstructure, interface and fabricating process of Al2O3-SiO2/AZ91D composites prepared by squeeze infiltration [J]. Hot Working Technology, 2009, 38(20): 53-56. (in Chinese)
[13] Yawny A, Eggeler G. Assessment of back stress and load transfer approaches for rationalizing creep of short fiber reinforced aluminum alloys [J]. Materials Science and Engineering A, 2004, 387-389: 905-909.
[14]  MOLL F. An evaluation of the creep characteristics of an AZ91 magnesium alloy composite using acoustic emission [J]. Materials Science and Engineering A, 2002, 338(1-2): 1-7.
MOLL F. An evaluation of the creep characteristics of an AZ91 magnesium alloy composite using acoustic emission [J]. Materials Science and Engineering A, 2002, 338(1-2): 1-7.
[15]  V, Svoboda M,
V, Svoboda M,  M,
M,  K, Langdon T G. Microstructural processes in creep of an AZ 91 magnesium-based composite and its matrix alloy [J]. Materials Science and Engineering A, 2001, 319-321: 741-745.
K, Langdon T G. Microstructural processes in creep of an AZ 91 magnesium-based composite and its matrix alloy [J]. Materials Science and Engineering A, 2001, 319-321: 741-745.
[16] Olbricht J, Yawny A, Young M L, Eggeler G. Mechanical and microstructural observations during compression creep of a short fiber reinforced AlMg metal matrix composite [J]. Materials Science and Engineering A, 2009, 510-511: 407-412.
[17] Spigarelli S, Mehtedi M E. Microstructure-related equations for the constitutive analysis of creep in magnesium alloys [J]. Scripta Materialia, 2009, 61(7): 729-732.
[18] Zhang J S. High-temperature deformation and fracture of materials [M]. Beijing: Science Press, 2007. (in Chinese)
[19] Ma Z Y, Tjong S C. The high-temperature creep behaviour of 2124 aluminium alloys with and without particulate and SiC-whisker reinforcement [J]. Composites Science and Technology, 1999, 59(5): 737-747.
[20] Wang Z X, Liu X F, Xie J X. Constitutive relationship of hot deformation of AZ91 magnestium alloy [J]. Acta Metallurgica Sinica, 2008, 44(11): 1378-1383. (in Chinese)
[21] Cadek J, Oikawa H, Sustek V. Threshold creep behaviour of discontinuous aluminium and aluminium alloy matrix composites: An overview [J]. Materials Science and Engineering A, 1995, 190(1-2): 9-23.
[22] LI Y, LANGDON T G. Creep behavior of an AZ91 magnesium alloy reinforced with alumina fibers [J]. Metallurgical and Materials Transactions A, 1999, 30(8): 2059-2066.
[23] Svoboda M, 
 V. The role of matrix microstructure in the creep behaviour of discontinuous fiber-reinforced AZ 91 magnesium alloy [J]. Materials Science and Engineering A, 2002, 324(1-2): 151-156.
V. The role of matrix microstructure in the creep behaviour of discontinuous fiber-reinforced AZ 91 magnesium alloy [J]. Materials Science and Engineering A, 2002, 324(1-2): 151-156.
[24] Spigarelli S, Cabibbo M, Evangelista E, Talianker M. Analysis of the creep behaviour of a thixoformed AZ91 magnesium alloy [J]. Materials Science and Engineering A, 2000, 289(1-2): 172-181.
[25] Tian S G, Wang L, Sohn K Y, Kim K H. Microstructure evolution and deformation features of AZ31 Mg-alloy during creep [J]. Materials Science and Engineering A, 2006, 415(1-2): 309-316.
田 君,石子琼
东莞理工学院 机械工程学院,东莞 523808
摘 要:利用常应力拉伸蠕变实验法对体积分数为30%的硅酸铝短纤维增强AZ91D镁基复合材料及其基体合金AZ91D在不同温度和应力下进行蠕变测试。结果表明:2种材料的真应力指数均为3,真蠕变激活能均等于144.63 kJ/mol;复合材料的蠕变是由基体的蠕变控制,以位错黏滞性滑移控制为主,晶界滑移控制为辅。由实验数据获得的蠕变本构模型的经验公式能较好地描述复合材料的蠕变变形规律。
关键词:镁基复合材料;门槛应力;有效应力;本构模型
(Edited by Chao WANG)
Foundation item: Project (10151170003000002) supported by the National Science Foundation of Guangdong Province, China
Corresponding author: Jun TIAN; Tel: +86-769-22861281; E-mail: 841608534@qq.com
DOI: 10.1016/S1003-6326(14)63105-8

