Springback prediction of TC4 titanium alloy V-bending under hot stamping condition
来源期刊:中南大学学报(英文版)2020年第9期
论文作者:王宝雨 杨晓明 党利明 王耀琦 周靖
文章页码:2578 - 2591
Key words:titanium alloy; hot stamping; springback; FE modelling; analytical model
Abstract: In this paper, the springback of TC4 titanium alloy under hot stamping condition was studied by means of experiment and numerical analysis. Firstly, an analytical model was established to predict the V-shaped springback angle Δα under the stretch-bending conditions. The model took into account of blank holder force, friction, property of the material, thickness of the sheet and the neutral layer shift. Then, the influence of several process parameters on springback was studied by experiment and finite element simulation using a V-shaped stamping tool. In the hot stamping tests, the titanium alloy sheet fractured seriously at room temperature. The titanium alloy has good formability when the initial temperature of the sheet is 750–900 °C. However, the springback angle of formed parts is large and decreases with increasing temperature. The springback angle Δα decreased by 50% from 0.5° to 0.25°, and the angle Δβ decreased by 46.7% from 1.5° to 0.8° when the initial temperature of sheet increased from 750 °C to 900°C. The springback angle of titanium alloy sheet increases gradually with the increase of the punch radius, because of the increase of elastic recovery, the complex distribution of stress, the length of forming region and the decreasing degree of stress. Compared with the simulation results, the analytical model can better predict the springback angle Δα.
Cite this article as: YANG Xiao-ming, DANG Li-ming, WANG Yao-qi, ZHOU Jing, WANG Bao-yu. Springback prediction of TC4 titanium alloy V-bending under hot stamping condition [J]. Journal of Central South University, 2020, 27(9): 2578-2591. DOI: https://doi.org/10.1007/s11771-020-4483-y.

J. Cent. South Univ. (2020) 27: 2578-2591
DOI: https://doi.org/10.1007/s11771-020-4483-y
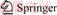
YANG Xiao-ming(杨晓明)1, DANG Li-ming(党利明)1, WANG Yao-qi(王耀琦)2,ZHOU Jing(周靖)1, 3, WANG Bao-yu(王宝雨)1, 3
1. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Metal Forming Technology Department, AVIC Manufacturing Technology Institute,Beijing 100024, China;
3. Beijing Key Laboratory of Metal Lightweight Forming Manufacturing, Beijing 100083, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: In this paper, the springback of TC4 titanium alloy under hot stamping condition was studied by means of experiment and numerical analysis. Firstly, an analytical model was established to predict the V-shaped springback angle △α under the stretch-bending conditions. The model took into account of blank holder force, friction, property of the material, thickness of the sheet and the neutral layer shift. Then, the influence of several process parameters on springback was studied by experiment and finite element simulation using a V-shaped stamping tool. In the hot stamping tests, the titanium alloy sheet fractured seriously at room temperature. The titanium alloy has good formability when the initial temperature of the sheet is 750–900 °C. However, the springback angle of formed parts is large and decreases with increasing temperature. The springback angle △α decreased by 50% from 0.5° to 0.25°, and the angle △β decreased by 46.7% from 1.5° to 0.8° when the initial temperature of sheet increased from 750 °C to 900°C. The springback angle of titanium alloy sheet increases gradually with the increase of the punch radius, because of the increase of elastic recovery, the complex distribution of stress, the length of forming region and the decreasing degree of stress. Compared with the simulation results, the analytical model can better predict the springback angle △α.
Key words: titanium alloy; hot stamping; springback; FE modelling; analytical model
Cite this article as: YANG Xiao-ming, DANG Li-ming, WANG Yao-qi, ZHOU Jing, WANG Bao-yu. Springback prediction of TC4 titanium alloy V-bending under hot stamping condition [J]. Journal of Central South University, 2020, 27(9): 2578-2591. DOI: https://doi.org/10.1007/s11771-020-4483-y.
1 Introduction
Springback of the sheet is the most serious and difficult problem in stamping process, because the shape of stamping parts after springback is related to the whole forming history. Titanium alloy has been extensively used for aerospace and aviation applications because of an attractive combination of properties such as high specific strength, excellent fracture toughness and good heat/corrosion resistance [1]. TC4 titanium alloy is by far the most popular one among titanium alloys [2]. However, the alloy is difficult to form into a complex part at room temperature due to its poor formability [3]. And the part has poor dimensional precision due to springback.
Traditional forming methods of titanium alloy,such as superplastic forming [4], creep aging forming [5], isothermal forming [6], and hot gas forming [7, 8] require a very high temperature of sheet, and heating of tools simultaneously. In addition, the strain rate (10-4-10-2 s-1) of titanium alloy sheets needs to be strictly controlled to prevent from forming defects in these processes. This means that the production efficiency of these processes is not high. It may not be able to meet the demand of the rapid growth of these aviation parts in the future. MOHAMED et al [9] and FOSTER et al [10] proposed a novel forming process named hot stamping and die quenching (HFQ ) to resolve the poor formability of aluminum alloy and reduce the springback of the part. In this process, the sheet firstly was heated for a certain time. Then, it will be transferred to the cold tool for forming and quenching concurrently. So far, this process has been widely used in automobile body manufacturing, such as AA6082 and AA5754 aluminum alloy. At present, the research on hot stamping process is still focused on aluminum alloy and high strength steel. However, few investigations have been reported focusing on the hot stamping of titanium alloy, which has excellent temperature stability and corrosion resistance[11]. In this study, the HFQ process was used to form titanium alloy parts due to its productive and good application in the aspect of controlling high strength steel and aluminum alloy springback.
) to resolve the poor formability of aluminum alloy and reduce the springback of the part. In this process, the sheet firstly was heated for a certain time. Then, it will be transferred to the cold tool for forming and quenching concurrently. So far, this process has been widely used in automobile body manufacturing, such as AA6082 and AA5754 aluminum alloy. At present, the research on hot stamping process is still focused on aluminum alloy and high strength steel. However, few investigations have been reported focusing on the hot stamping of titanium alloy, which has excellent temperature stability and corrosion resistance[11]. In this study, the HFQ process was used to form titanium alloy parts due to its productive and good application in the aspect of controlling high strength steel and aluminum alloy springback.
In order to study the applicability of hot stamping process in titanium alloy forming, the high temperature deformation behaviors of titanium alloy must be studied. The flow stress increases with increasing the temperature and decreasing the strain rate in the temperature ranging from 880 °C to 950 °C and strain rate ranging from 1 s-1 to 50 s-1 [12]. The mainly flow softening behavior mechanisms of titanium alloy are phase transforming, dynamic recrystallization and dynamic recovery. The flow softening behavior can be promoted by increasing the material temperature [13-15].
Springback is a geometrical and dimensional inaccuracy in sheet metal formed components between the fully loaded and unloaded configurations, which can lead to inaccurate assembly [16]. Titanium alloy parts are more likely to springback because of its high yield strength and low elastic modulus [17]. The springback rules can be obtained by experimental tests. And the experimental study of simple parts can guide to forming the complex accurately. CHEN et al [18] found that the springback angle of pure titanium is small at small punch radius and high deformation temperature by V-shaped bend tests. However, the negative springback angles occur in the smaller punch radius because of the complex stress distribution of the side wall. Therefore, the radius of punch should be appropriately chosen. ZHAO et al [19] studied the effect of electron pulse on springback of Ti6Al4V alloy. It was found that 30% duty cycle had a great effect on springback angle of forming parts, and 30% duty cycle can reduce residual stress by 50%. It is indicated that the deformation temperature of sheet is not the only factor to reduce springback in the electric current treatment. AO et al [20] also studied the effect of electropulsing on springback of Ti6Al4V alloy. It was found that the distribution of β-phase particles was contributing to reduce springback by observing the microstructure of inner, neutral and outer layers of the formed parts. ZONG et al [21] studied the effects of sheet temperature, punch radius and holding time on springback of Ti6Al4V alloy under isothermal forming conditions. It is found that the increasing of holding time could greatly reduce the springback angles due to the internal stress relaxation. GHEYSARIAN et al [22] found that application of annealing before aging can effectively reduce the springback of Ti6Al4V alloys. There is a lot of research on the influence of process on titanium alloy springback. Therefore, the experimental schemes are determined based on the existing experimental research. At present, due to the emergence of new research methods and new processes, the existing research on Ti6Al4V alloy has been unable to adopt the current development. Although the forming tests can obtain accurate springback law, it takes a lot of time and cost. Therefore, it is necessary to establish an analytical model of sheet and predict its springback. Up to now, some researchers used analytical model to theoretically analyze and predict the springback of the sheet. The springback of DP600 was predicted using simulation with multiple cyclic stress–strain curves proposed by UI et al [23]. Comparing to the other models with single stress-strain curve, the simulation model with multiple cyclic stress- strain curves has higher prediction accuracy in Ref. [23]. The Bauschinger effect is a description of the change of residual stress. The Bauschinger effect should be considered in the analytical model for accurate prediction of springback. GAU et al [24] established a new model considering the Bauschinger effect. And the springback of AA6111 can be well predicted by using this model. An analytic model that can calculate the large strain was proposed by ALEXANDROV et al [25]. Simultaneously, the distribution of residual stress was studied in the sheet cross-section. An analytical model was described the springback of advanced high strength steel (DP780) by YANG et al [26]. The influence of the elastic modulus, material constant K and the hardening exponent n on the springback was analyzed. It draw conclusions that elastic modulus is a variable in bending process and the prediction accuracy can be improved by more accurate expression of elastic modulus changing. CHATTI et al [27] used three hardening models and modified Yushida-Uemori model to predict the springback angles of L-bending and U-bending tests, respectively. The results show that the combination of non-kinematic hardening and Yushida-Uemori model can better predict the springback of parts. The release of residual stress is other reason to cause springback except elastic recovery. Therefore, the distribution of stress is important in the springback prediction model. The modelling considering hardening law and yield criteria was established by EGGERTSEN et al [28]. The results show that Y-U model can better fit the change of the stress in the bending process. However, the Y-U model is high complex. Therefore, the Gen- Wagoner is selected due to its prediction accuracy and low complexity. In engineering application, the springback is not a single direction, but multiple directions. PARSA et al [29] established a prediction model considering the change of sheet thickness and the displacement of neutral surface to predict the double curved springback. Similarly, XUE et al [30] proposed an analytical model that can predict the springback in the process of double-curvature forming.
In this paper, the analytical model was proposed to describe the springback of V-shaped under the stretch-bending conditions. Then, the hot tensile tests were conducted at temperature ranging from 750 °C to 900 °C and strain rate ranging from 0.01 s-1 to 1 s-1. The springback features of TC4 titanium alloy at deformation temperature ranging from 750 °C to 900 °C and punch radius ranging from 5 mm to 30 mm were studied by V-shaped tool. And the change of stress was analyzed by finite element simulation under loading and unloading conditions.
2 Experimental details
2.1 Material
The experimental material was TC4 annealed titanium alloy with a thickness of 1.6 mm. The initial microstructure of the sheet is shown in Figure 1. It can be seen that β-phase is dispersed in the α-phase matrix.

Figure 1 SEM image of TC4 annealed titanium alloy
2.2 Uniaxial hot tensile tests
The hot tensile tests were conducted on a Gleeble-1500 thermal simulation machine to characterize the flow behavior of TC4 titanium alloy. The specimens were fixed within high thermal conductivity grips, clamped within jaws having embedded water-cooling. A pair of thermocouples was welded to each specimen to provide signals for accurate feedback control of the specimen temperature. Figure 2(a) shows the testing fixture and the dimensions of the specimen. Specimens used in the hot tensile test were previously machined by wire-electrode cutting. The length direction is the rolling direction.
In the hot tensile test, in order to prevent the heating temperature from exceeding the deformation temperature because the heating speed of the sample is too fast, the following test scheme is adopted: Firstly, the specimens were heated to a temperature 25 °C lower than the deformation temperature at a heating rate of 20 °C/s. Then, the specimens were heated to the forming temperature at a rate of 5 °C/s and soaked for 180 s to guarantee uniform temperature distribution in all parts of the sample. After the specimens were fully heated, the specimens were stretched to failure. The samples were quenched immediately after fracturing to retain its high temperature microstructure. The deformation temperatures were 750, 800, 850 and 900 °C. The strain rates were 0.01, 0.1 and 1 s-1. The experimental route is shown in Figure 2(b).
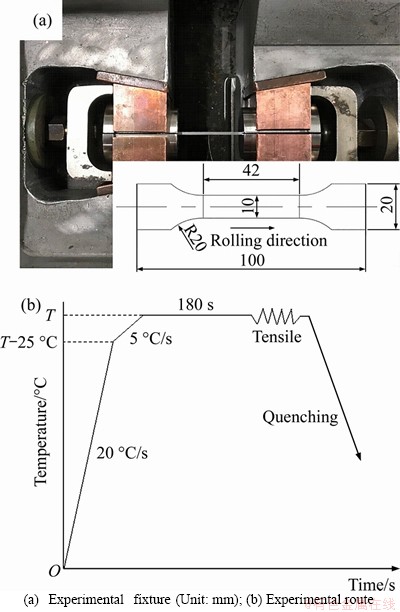
Figure 2 Hot tensile test:
The resistance heating mode was used in Gleeble-1500 thermal simulation machine, and the temperature distribution in the length direction was non-uniform. Therefore, the isothermal region of the sample was considered as 10 mm in the middle of the sample shown in Figure 3, and the stress- strain curve was calculated and modified by the following formula.

Figure 3 Hot tensile sample
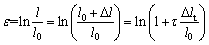 (1)
(1)
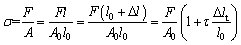 (2)
(2)
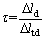 (3)
(3)
where σ and ε represent the true stress and true strain, respectively; A and l represent the instantaneous cross sectional area and length of isothermal region, respectively; A0 and l0 represent the initial cross sectional area and length of isothermal region, respectively; △l and △lt represent the instantaneous extension length of isothermal region and the instantaneous extension length of the sample, respectively; τ is the conversion coefficient; △ld and △ltd are the extension length of isothermal region and the extension length of the sample, respectively, after fracture.
2.3 Hot V-bending test
Due to the fact that the traditional forming method of titanium alloy sheet is isothermal forming and superplastic forming, there are few reports on springback of titanium alloy under hot stamping conditions. A V-shaped tool was used to investigate springback of Ti6Al4V alloy in the hot stamping conditions. The V-shaped tool is shown in Figure 4. Before the tests, the titanium alloy sheet was cut into a sample having dimensions of 180 mm×50 mm×1.6 mm. Then, the sheet was spread with the glass lubricant on both sides to reduce the friction. During the hot stamping test, the titanium alloy sheet was placed in a heating furnace and heated to forming temperature ranging from 750 °C to 900 °C for 300 s. Then, the sheet was rapidly transferred to the blank holder, and the 60 t press worked to complete the stamping. The blank holder was supported by a gas spring and exerted blank holder force on the sheet. After the stamping, the sheet was held between the cold punch and die to quench for 30 s, ensuring sufficient cooling of the sheet. Parameters of hot stamping are shown in Table 1.

Figure 4 V-shaped tool
Table 1 Parameters of hot stamping

The springback angle is shown in Figure 5. The change of forming region angle △α and blank holder region angle △β is mainly studied. The angles to be measured after forming are △ and △β, respectively. However, directly measuring △β is difficult, so γ is measured and the following formula is adopted to calculate the springback angles and α is the tool design angle.
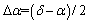
 (4)
(4)

Figure 5 Angles defining springback for V-shape bending
3 Stress–strain curves and FE model
3.1 True stress–strain curves
Figure 6 shows the true stress-strain curves of TC4 titanium alloy corresponding to different deformation conditions. It can be seen from the figure that the stress-strain curves can be divided into three stages: elastic deformation, work hardening and softening.
Both deformation temperatures and strain rates affect the flow stress of TC4 titanium alloy. At the same deformation temperature, with the increase of strain rate, the cumulative rate of dislocation increases gradually, and the ability of dislocation recovery at high strain rate is weaker than that at low strain rate. As the deformation increases, the dislocation density in the material increases, which restraints the plastic flow of the material. Eventually, the flow stress of the material increases gradually. At the same strain rate, the flow stress decreases with the increase of deformation temperature. And with the increase of deformation temperature, the α-phase with higher strength gradually transforms to a β-phase with lower strength, which is one of the reasons for material softening during the tensile tests except dynamic recovery and recrystallization [31].
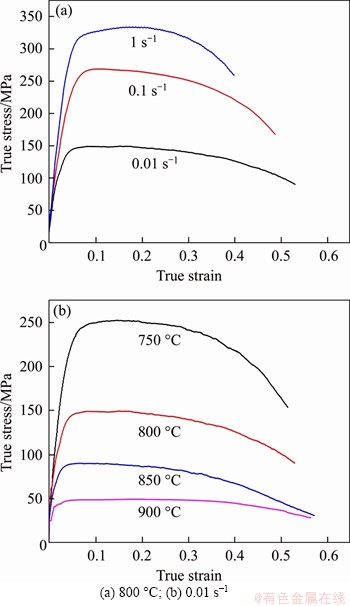
Figure 6 Stress–strain curves:
3.2 FE model
The finite element simulation software Pam-stamp was used to establish the finite element model of the V-shape part. Since the formed part is symmetry, half of the cut-out part was modeled. In the FE simulation, the HFQ process was divided into five stages: aircooling, holding, stamping, die quenching and springback. The simulation process is shown in Figure 7.
process was divided into five stages: aircooling, holding, stamping, die quenching and springback. The simulation process is shown in Figure 7.

Figure 7 Process of FE simulation
In the model, the sheet elements are elastic-plastic elements with the mesh size of 0.1 mm and the material stress-strain curve adopts the curve shown in Figure 5. The elastic modulus is 110 GPa. Density of TC4 titanium alloy is 4.51 g/cm3. The other physical properties of the materials are shown in Table 2. In order to simplify the calculation, the tools were set to be a rigid body, with an average element size of 2 mm, and the initial temperature of the tool is set to room temperature. The friction coefficient between the sheet and the tool is set to a fixed value of 0.15. The heat transfer coefficient which was measured by BAI et al [32] was used in this model.
Table 2 Physical parameters of TC4 titanium alloy

In the experiment, the die material is H13. In the simulation model, H13 is also selected as the tool material with a density of 7.8 g/cm3 in order to ensure the accuracy of finite element simulation. The change of physical parameters with temperature is shown in Table 3.
Table 3 Physical parameters of H13

4 Analytical model
In the experimental tests, the sheet was subjected to the bending moment M and the force F because of the friction. The deformation of TC4 titanium alloy can be considered a stretch-bending problem. And the stretch-bending modes are shown in Figure 8. Under the action of the stretch force F, the tensile stress of the outer layer increases, the compressive stress of the inner layer decreases, the neutral layer of the sheet moves toward the inner layer, and the neutral layer moves from the middle surface y=0 to the neutral surface y=yT.
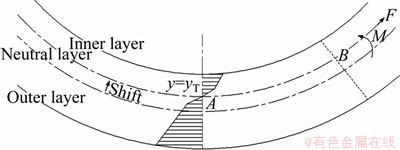
Figure 8 Stretch-bending mode
The loading moment can be calculated by:
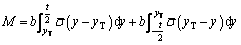 (5)
(5)
where the yT is the moving distance of neutral layer due to the influence of tensile force; b is the width of blank;  is the equivalent stress which is composed of plastic stress and stretching stress (σF=F/A); A is the area of the blank cross-section; F is the stretching force due to the friction and it can be described by [27]:
is the equivalent stress which is composed of plastic stress and stretching stress (σF=F/A); A is the area of the blank cross-section; F is the stretching force due to the friction and it can be described by [27]:
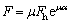 (6)
(6)
where Fh is the blank holder force; μ is the friction coefficient between tool and blank; α is the mold design angle.
And the plastic flow stress can be described by
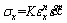 (7)
(7)
where K is the material constant; n is the strain hardening exponent; m is strain rate sensitivity coefficient. The relationships between the three parameters and temperature are respectively described by
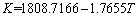 (8)
(8)
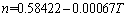 (9)
(9)
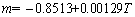 (10)
(10)
εx is the longitudinal strain which can be calculated by
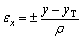 (11)
(11)
where ρ is the curvature radius of neutral layer before springback; “±” denotes the stress state in the cross-section; “+” denotes the tensile stress state; “-” denotes the compressive stress state.
As a result, Eq. (5) can be modified as
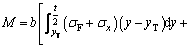

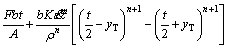 (12)
(12)
There will be elastic recovery on the region AB when the loading is removing. After unloading, the part rebounds because of the elastic recovery. The springback caused by elastic recovery is equivalent to the reverse bending moment applied in the deformation zone. The springback value can be calculated by

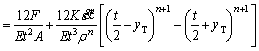 (13)
(13)
where E is the elastic modulus; I is the moment of inertia; ρ0 is the curvature radius of neutral layer after springback.
The angle after springback can be expressed by
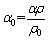 (14)
(14)
As a result, the springback angle can be calculated by
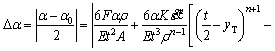
 (15)
(15)
5 Results and discussion
5.1 Effect of temperature on springback
Figure 9 shows the forming parts at different initial temperatures when the radius of the punch is 5 mm. It can be seen that the titanium alloy sheet has serious fracture at room temperature. The titanium alloy has good formability when the initial temperature of the sheet is between 750 °C and 900 °C. This is because titanium alloy is mainly composed of high strength α-phase at room temperature, and the plastic is poor. With the increase of temperature, the α-phase with hexagonal close-packed crystal structure transforms into β-phase with body-centered cubic crystal structure, and the material plastic increases, which makes it easier to deform.
Although, the springback angle decreases gradually with the increase of initial temperature of sheet, the formed part still has a large springback angle, because the temperature of the sheet drops rapidly as the sheet material is transferred from the furnace to the die. The temperature distribution of blank was observed by infrared thermal camera during transferring and holding. The initial blank temperature is 850 °C. The temperature distribution is shown in Figure 10. It can be seen that the distribution of temperature has good consistency between experimental test and finite element analysis. The distribution of blank temperature along the length of sheet is shown in Figure 10(e) after stamping. The temperature in the side wall is higher than the other regions due to less contacting with the tool. The blank holder region has the lower temperature because of the long time contacting with the tool. The inhomogeneous distribution of sheet temperature results in the appearance of residual stress. The release of residual stress increases the springback after unloading.

Figure 9 Forming parts at different initial temperatures:
The prediction model is only used to predict the springback angle △α, because the angle △β is affected by many factors, such as side wall and the angle △α. Figure 11 shows the comparisons of springback angles between prediction and experimental results at different initial temperatures of sheet. It can be seen that the analytical model can better predict the change of angle △α compared with the simulation results. According to the experimental results, when the initial temperature of sheet increased from 750 °C to 900 °C, the springback angle △α decreased by 50% from 0.5° to 0.25°, and the angle △β decreased by 46.7% from 1.5° to 0.8°. It can be considered that increasing the initial temperature of sheet is beneficial to the reduction of springback angle. This is because the yield strength of the material decreases with the increase of the sheet temperature. In the process of deformation, the elastic deformation energy will be accumulated when the deforming force is smaller than the yield strength of the material. When the deforming force exceeds the material yield strength, the plastic deformation energy will be accumulated, which is the permanent deformation of the sheet. Under the same deformation conditions, higher temperature can make the sheet accumulate more plastic deformation energy. The higher plastic deformation energy makes more plastic deformation under the same deformation conditions. And the elastic deformation will decrease so that the elastic recovery will decrease. Therefore, the springback angles will reduce.
The change of equivalent stress is shown in Figure 12 under loading and unloading conditions. It can be seen that the equivalent stress has reduced after springback. And it concludes that the change of the equivalent stress is another important reason for the change of the springback angles. The equivalent stress in the CD region is larger than other regions because of the bending moment. On the other hands, the stress in the CD region is also affected by the stress in the AB region and BC region. Therefore, the springback angle △β in blank holder region is larger than the angle △α in the forming region. And it can be seen that the reduction of the equivalent stress near in the CD region is larger than that in the AB region. So, the springback angle of the CD region is large comparing to the AB region. In addition, with the increase of the sheet temperature, the change range of the equivalent stress decreases before and after springback. In AB region, the equivalent stress decreases from 125.45 MPa to 90.03 MPa at 750 °C. The equivalent stress decreases from 37.58 MPa to 32.05 MPa at 900 °C. Therefore, the release of equivalent stress is smaller at higher temperature, and the springback of sheet is smaller after unloading.
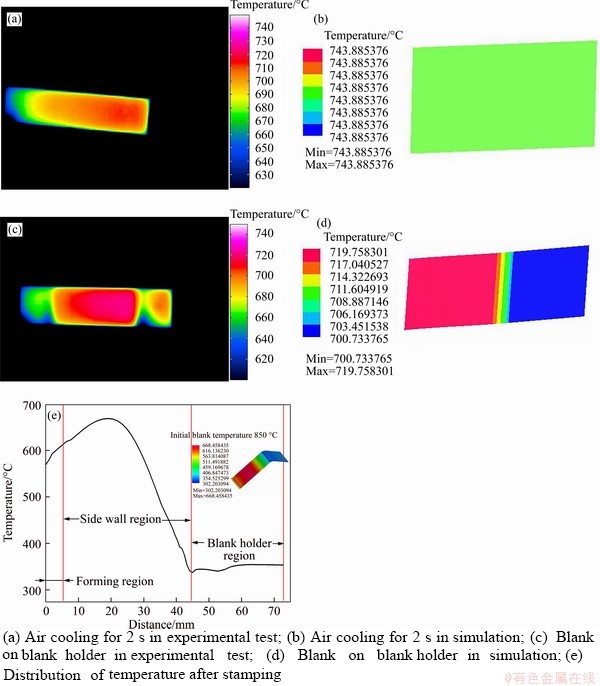
Figure 10 Comparison of experimental and simulation results:
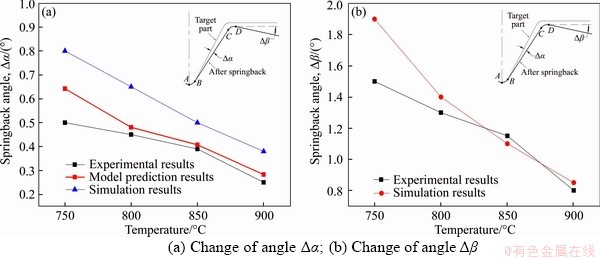
Figure 11 Comparisons between prediction and experimental results at different temperatures:
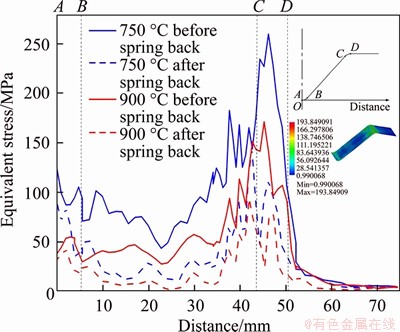
Figure 12 Change of equivalent stress at different temperatures
5.2 Effect of punch radius on springback
Figure 13 shows the formed parts using hot stamping and cold die quenching process at different punch radii when the sheet temperature is 800 °C. The TC4 titanium alloy sheet has good formability under different punch radii. However, as the radius of the punch increases, the formed part rebounds. When the radius of punch increases, the localized plastic deformation of material decreases, and a large number of elastic deformation remains in the forming part. After the die was removed, the elastic deformation recovery and residual stress release lead to the increase of springback [33].

Figure 13 Forming parts at different punch radii at 800 °C:
The influence of the punch radius on the springback angle is shown in Figure 14 when the initial blank temperature is 800 °C. It can be seen that the springback angle increases rapidly with the increase of punch radius. According to the experimental results, the angle △α increased from 0.45° to 8.5°, and the angle △β increased from 1.3° to 7.1°, as the punch radius increased from 5 mm to 30 mm. Large radius of punch is not conducive to hot stamping of titanium alloy, so proper radius of punch should be selected in hot stamping of titanium alloy. The analytical model has a good prediction precision.
The springback of sheet occurs in the unloading process, so it is necessary to analyze the variation of stress in the deformed zone of bending sheet metal during unloading process. Under the action of bending moment, the internal layer of sheet is compressive stress and the external layer of sheet metal is tensile stress. The elastic recovery after unloading can be considered adding an imaginary elastic moment in the opposite direction of the plastic moment. Therefore, the internal stress of sheet metal is tensile stress and the external stress of sheet metal is compressive stress when the elastic moment applies on the parts. When the elastic bending moment acts on the sheet metal, the elastic deformation restores and remains in the sheet metal to form residual stress. In hot stamping test of titanium alloy, with the increase of punch radius, the bending length of V-shaped parts at the corner of punch gradually increases, the degree of plastic deformation decreases, the plastic bending moment decreases, and the elastic bending moment increases [34]. Under the effect of elastic deformation recovery and residual stress release, the springback angle of forming parts increases gradually.
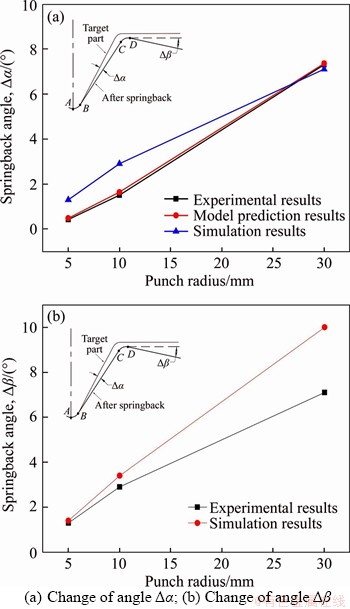
Figure 14 Comparisons between prediction and experimental results at different punch radii:
The comparison of equivalent stress at different punch radii is shown in Figure 15. The equivalent stress of forming region at punch radius 5 mm and 30 mm is in AB1 and AB2 region respectively. It can be seen that the distribution of TC4 titanium alloy equivalent stress becomes complex and the stress increases with the punch radius increasing. The fluctuation of equivalent stress is not obvious at punch radius 5 mm, but the stress fluctuation in the forming area is obvious when the punch radius increases to 30 mm, which leads to the increase of springback after unloading. The reduction of equivalent stress is greatly high at punch radius 30 mm comparing with punch radius 5 mm. In forming region, the equivalent stress decreases from 89.45 to 73.14 MPa at punch radius 5 mm. The equivalent stress decreases from 120.47 to 80.87 MPa at punch radius 30 mm. Finally, the springback angle increases at high punch radius due to the complex distribution of stress, the length of forming region and the decreasing degree of stress.

Figure 15 Comparison of equivalent stress at punch radius 5 mm and 30 mm
6 Conclusions
1) According to the prediction model, it is found that the change of springback angle of sheet metal is influenced by the properties of sheet metal, radius of the punch, blank holder force, friction coefficient and thickness of sheet metal. The prediction model established in this paper can better predict the springback angle △α by comparing the results of the prediction model and the simulation.
2) Compared with cold forming, TC4 titanium alloy can be better formed by hot stamping process. With the increase of initial blank temperature, the springback angle △α decreased by 50% from 0.5° to 0.25°, and the angle △β decreased by 46.7% from 1.5° to 0.8°. The springback angle of the titanium alloy V-parts increases gradually with the increase of the punch radius. Especially when the punch radius is 30 mm, the springback angle is 8.5°. In this study, the initial temperature of sheet is 900 °C and the punch radius is 5 mm, which can obtain better forming quality and precision.
3) According to the simulation results, it can be seen that the inhomogeneous distribution of sheet temperature and equivalent stress increases the springback after unloading.
Contributors
The overarching research goals were developed by YANG Xiao-ming, WANG Yao-qi, WANG Bao-yu and ZHOU Jing, and YANG Xiao-ming and DANG Li-ming provided the experimental data, and analyzed the experimental data. YANG Xiao-ming and ZHOU Jing established the predicted model and simulation model.The initial draft of the manuscript was written by YANG Xiao-ming. All authors replied to reviewers & apos; comments and revised the final version.
Conflict of interest
YANG Xiao-ming, DANG Li-ming, WANG Yao-qi, ZHOU Jing and WANG Bao-yu declare that they have no conflict of interest.
References
[1] GRUN P A, UHEIDA E H, LACHMANN L, DIMITROV D, OOSTHUIZEN G A. Formability of titanium alloy sheets by friction stir incremental forming [J]. International Journal of Advanced Manufacturing Technology, 2018, 99: 1993-2003. DOI: https://doi.org/10.1007/s00170-018-2541-5.
[2] YANG Xia-wei, FENG Wu-yuan, LI Wen-ya, CHU Qiang, XU Ya-xin, MA Tie-jun, WANG Wei-bing. Microstructure and mechanical properties of dissimilar pinless friction stir spot welded 2A12 aluminum alloy and TC4 titanium alloy joints [J]. Journal of Central South University, 2018, 25(12): 3075-3084. DOI: https://doi.org/10.1007/s11771-018-3975- 5.
[3] PARK N K, YEOM J T, NA Y S. Characterization of deformation stability in hot forging of conventional Ti-6Al-4V using processing maps [J]. Journal of Materials Processing Technology, 2002, 130: 540-545. DOI: https:// doi.org/10.1016/S0924-0136(02)00801-4.
[4] PITT F, RAMULU M. Influence of grain size and microstructure on oxidation rates in titanium alloy Ti6Al4V under superplastic forming conditions [J]. Journal of Materials Engineering and Performance, 2004, 13(6): 727-734. DOI: https://doi.org/10.1361/10599490421394.
[5] DENG T, LIU D, LI X, DING P, ZHAO K. Hot stretch bending and creep forming of titanium alloy profile [J]. Procedia Engineering, 2014, 81: 1792-1798. DOI: https://doi.org/10.1016/j.proeng.2014.10.234.
[6] GAO P F, YANG H, FAN X G, YAN S L. Microstructural features of TA15 titanium alloy under different temperature routes in isothermal local loading forming [J]. Materials Science and Engineering A, 2012, 540(1): 245-252. DOI: https://doi.org/10.1016/j.msea.2012.02.006.
[7] WU Yong, LIU Gang, JIN Shou-yi, LIU Zhi-qiang. Microstructure and mechanical properties of Ti2AlNb cup-shaped part prepared by hot gas forming: Determining forming temperature, strain rate, and heat treatment [J]. International Journal of Advanced Manufacturing Technology, 2017, 92: 4583-4594. DOI: https://doi.org/10. 1007/s00170-017-0501-0.
[8] WANG Guo-feng, LI Xiao, LIU Si-yu, GU Yi-bin. Improved superplasticity and microstructural evolution of Ti2AlNb alloy sheet during electrically assisted superplastic gas bulging [J]. International Journal of Advanced Manufacturing Technology, 2018, 99: 773-787. DOI: https://doi.org/10.1007/s00170-018-2431-x.
[9] MOHAMED M S, FOSTER A D, LIN J G, BALINT D S, DEAN T A. Investigation of deformation and failure features in hot stamping of AA6082: Experimentation and modelling [J]. International Journal of Machine Tools and Manufacture, 2012, 53(1): 27-38. DOI: https://doi.org/10.1016/ j.ijmachtools. 2011.07.005.
[10] FOSTER A, DEAN T A, LIN J. Process for forming aluminum alloy sheet components: European Patent; EP2324137 [P]. 2013-10-09.
[11] WILLIAMS J C, STARKE E A Jr. Progress in structural materials for aerospace systems [J]. Acta Materialia, 2003, 51(19): 5775-5799. DOI: https://doi.org/10.1016/j.actamat. 2003. 08.023.
[12] BRUSCHI S, POGGIO S, QUADRINI F, TATA M E. Workability of Ti6Al4V alloy at high temperatures and strain rates [J]. Materials Letters, 2004, 58(27, 28): 3622-3629. DOI: https://doi.org/10.1016/j.matlet.2004.06.058.
[13] SUN Sheng-di, ZONG Ying-ying, SHAN De-bin, GUO Bin. Hot deformation behavior and microstructure evolution of TC4 alloy titanium alloy [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(11): 2181-2184. DOI: https://doi.org/10.1016/S1003-6326(09)60439-8.
[14] MOMENI A, ABBASI S M. Effect of hot working on flow behavior of Ti-6Al-4V alloy in single phase and two phase regions [J]. Materials & Design, 2010, 31: 3599-3604. DOI: https://doi.org/10.1016/j.matdes.2010.01.060.
[15] QUAN Guo-zheng, LUO Gui-chang, LIANG Jian-tian, WU Dong-sen, MAO An, LIU Qing. Modelling for the dynamic recrystallization evolution of Ti6Al4V alloy in two-phase temperature range and a wide strain rate range [J]. Computational Materials Science, 2015, 97: 136-147. DOI: https://doi.org/10.1016/j.commatsci.2014.10.009.
[16] WANG Yao, LANG Li-hui, LAURIDSEN S, KAN Peng. Springback analysis and strategy for multi-stage thin-walled parts with complex geometries [J]. Journal of Central South University, 2017, 24(7): 1582-1593. DOI: 10.1007/s11771- 017-3563-0.
[17] LI Qiao-chu, MIN Xiao-hua, BAI Peng-fei, WANG Wei-qiang, TAO Xiao-jie, ZHONG Gong-cheng, BAI Shu-yu, ZHAO Jie. Microstructure, mechanical properties and springback behavior of Ti-6Al-4V alloy connection rod for spinal fixation device [J]. Materials Science and Engineering C, 2019, 94: 911-820. DOI: https://doi.org/ 10.1016/j.msec.2018. 10.030.
[18] CHEN F K, CHI K H. Stamping formability of pure titanium sheets [J]. Journal of Material Processing Technology, 2005, 170: 181-186. DOI: https://doi.org/10.1016/j.jmatprotec. 2005.05.004.
[19] ZHAO Yi-xi, PENG Lin-fa, LAI Xin-min. Influence of the electric pulse on springback during stretch U-bending of Ti6Al4V titanium alloy sheets [J]. Journal of Materials Processing Technology, 2008, 261: 12-23. DOI: https://doi. org/10.1016/j.jmatprotec.2018.05.030.
[20] AO Dong-wei, CHU Xiong-rong, YANG Yang, LIN Shu-xia, GAO Jun. Effect of electropulsing on springback during V-bending of Ti-6Al-4V titanium alloy sheet [J]. International Journal of Advanced Manufacturing Technology, 2018, 96: 3197-3207. DOI: https://doi.org/10. 1007/s00170-018-1654-1.
[21] ZONG Ying-ying, LIU Po, GUO Bin, SHAN De-bin. Springback evaluation in hot v-bending of Ti-6Al-4V alloy sheets [J]. International Journal of Advanced Manufacturing Technology, 2015, 76: 577-585. DOI: https://doi.org/10. 1007/s00170-018-1654-1.
[22] GHEYSARIAN A, ABBASI M. The effect of aging on microstructure, formability and springback of Ti6Al4V titanium alloy [J]. Journal of Materials Engineering and Performance, 2017, 26: 374-382. DOI: https://doi.org/ 10.1007/s11665-016-2431-7.
[23] UI H H, TRAPHONER H, GUNER A, TEKKAYA A E. Accurate springback prediction in deep drawing using pre-strain based multiple cyclic stress-strain curves in finite element simulation [J]. International Journal Mechanical Sciences, 2015, 110: 229-241. DOI: https://doi.org/10.1016/ j.ijmecsci.2016.03.014.
[24] GAU J T, KINZEL G L. A new model for springback prediction in which the Bauschinger effect is considered [J]. International Journal of Mechanical Sciences, 2001, 43: 1813-1832. DOI: https://doi.org/10.1016/S0020-7403(01)00 012-1.
[25] ALEXANDROV S, MANABE K, FURUSHIMA T. A general analytic solution for plane strain bending under tension for strain-hardening material at large strains [J]. Archive of Applied Mechanics, 2011, 81: 1935-1952. DOI: https://doi.org/10.1007/s00419-011-0529-9
[26] YANG Xi, CHOI C, SEVER N K, ALTAN T. Prediction of springback in air-bending of Advanced High Strength steel (DP780) considering Young’s modulus variation and with a piecewise hardening function [J]. International Journal of Mechanical Sciences, 2016, 105: 266-272. DOI: https://doi. org/10.1016/j.ijmecsci.2015.11.028.
[27] CHATTI S, HERMI N. The effect of non-linear recovery on springback prediction [J]. Computers and Structures, 2011, 89: 1367-1377. DOI: https://doi.org/10.1016/j.compstruc. 2011.03.010.
[28] EGGERTSEN P A, MATTIASSON K. On the modelling of the bending-unbending behavior for accurate springback predictions [J]. International Journal of Mechanical Sciences, 2009, 51: 547-563. DOI: https://doi.org/10.1016/j.ijmecsci. 2009.05.007.
[29] PARSA M H, AHKAMI S N A, PISHBIN H, KAZEMI M. Investigating springback phenomena in double curved sheet metals forming [J]. Materials and Design, 2012, 41: 326-337. DOI: https://doi.org/10.1016/j.matdes.2012.05.009.
[30] XUE P, YU TX, CHE E. An energy approach for predicting springback of metal sheets after double-curvature forming - Part II: Unequal double curvature forming[J]. Int J Mech Sci, 2001, 43: 1915-1924. DOI: https://doi.org/10.1016/S0020- 7403(01)00004-2.
[31] ZHANG Song, LIANG Yi-long, XIA Qi-fan, OU Mei-gui. Study on tensile deformation behavior of TC21 titanium alloy [J]. Journal of Materials Engineering and Performance, 2019, 28: 1581-1509. DOI: https://doi.org/10.1007/s11665- 019-03901-x.
[32] BAI Q, LIN J, ZHAN L, DEAN T A, BALINT D S, ZHANG Z. An efficient closed-form method for determining interfacial heat transfer coefficient in metal forming [J]. International Journal of Machine Tools and Manufacture, 2012, 56: 102-110. DOI: https://doi.org/10.1016/ j.ijmachtools.2011.12.005.
[33] WANG Ai-ling, ZHONG Kai, EI FAKIR O, LIU Jun, SUN Chao-yang, WANG Li-liang, LIN Jian-guo, DEAN T A. Springback analysis of AA5754 after hot stamping: Experiments and FE modelling [J]. International Journal of Advanced Manufacturing Technology, 2017, 89: 1339-1352. DOI: https://doi.org/10.1007/s00170-016-9166-3.
[34] MA Wei-ping, WANG Bao-yu, XIAO Wen-chao, YANG Xiao-ming, KANG Yi. Springback analysis of 6016 aluminum alloy sheet in hot V-shape stamping [J]. Journal of Central South University, 2019, 26(3): 524-535. DOI: https://doi.org/10.1007/s11771-019-4024-8.
(Edited by YANG Hua)
中文导读
TC4钛合金V形件弯曲热冲压回弹预测
摘要:本文通过实验和数值分析的方法,研究了TC4钛合金在热冲压条件下的回弹。首先,建立了拉弯条件下V形件回弹角△α的分析模型。该模型考虑了压边力、摩擦、材料性能、板料厚度和中性层偏移等因素。然后,采用V形冲压模具,通过试验和有限元模拟研究了不同工艺参数对零件回弹的影响。在热冲压试验中,钛合金板在室温下成形出现严重断裂的现象。当板料初始温度为750~900 °C时,钛合金具有较好的成形性,但成形件的回弹角较大,且随着温度的升高而减小。当板料初始温度从750 °C升高到900 °C时,回弹角△α从0.5°减小到0.25°,减小了50%,回弹角△β从1.5°减小到0.8°,减小了46.7%。由于板料弹性恢复的增大,应力的复杂分布和成形区的长度及应力变化,导致钛合金板料的回弹角随着凸模半径的增大而逐渐增大。与仿真结果相比,分析模型能较好地预测回弹角△α的变化。
关键词:钛合金;热冲压;回弹;有限元模型;分析模型
Foundation item: Projects(U1564202, 51705018) supported by the National Natural Science Foundation of China; Project supported by the Beijing Laboratory of Modern Transportation Metal Materials and Processing Technology and the Beijing Key Laboratory of Metal Forming Lightweight, China
Received date: 2019-09-22; Accepted date: 2020-02-04
Corresponding author: WANG Bao-yu, PhD, Professor; Tel: +86-10-62332332; E-mail: bywang@ustb.edu.cn; ORCID: https://orcid. org/0000-0003-0462-9511

