set ts=-ts;
When |Si-1+ts|≤M-dt and Si-1>ρ,
set ts=ts+dt;
When |Si-1+ts|≤M-dt and Si-1<-ρ,
set ts=ts–dt.
Secondly calculate shifting position:
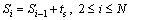 (11)
(11)
where ts is the basic shifting step; dt is the shifting step increment; Si is the shifting position of the i-th strip; N is the stroke reduction starting point; M is the maximum of shifting stroke; ρ is a small positive number.
2) The second phase of a rolling campaign
Start from the (N+1)-th strip, firstly update shifting step:
When Si-1+ts>kS(i)-dt or Si-1+tsS(i),
set ts =-ts;
When |Si-1+ts|≤kS(i)-dt and Si-1>ρ,
set ts =ts +dt;
When |Si-1+ts|≤kS(i)-dt and Si-1<-ρ,
set ts =ts–dt.
There is kS(i)=M–M·A·(i-N).
Secondly, calculate the shifting position:
 (12)
(12)
where A is the shifting stroke reduction rate; M and p are the known parameters for a specific rolling campaign; ts, dt, N and A are shifting control parameters, which decide roll shifting strategy.
When dt>0, the algorithm gets shifting strategy with varying step; when N
0, the algorithm gets shifting strategy with varying stroke. Only when dt>0 and N
0, the algorithm gets shifting strategy with varying stroke and varying step.
3.2 Comparison of four types of shifting strategy
Four types of shifting strategy can be gained by limiting the range of shifting control parameters:
1) When dt=0 and A=0, shifting strategy with fixed stroke and fixed step is obtained.
2) When dt=0 and A>0, shifting strategy with varying stroke and fixed step is obtained.
3) When dt>0 and A=0, shifting strategy with fixed stroke and varying step is obtained.
4) When dt>0 and A>0, shifting strategy with varying stroke and varying step is obtained.
Two characteristic parameters are compared in rolling process for four types of shifting strategy by numerical simulation. Take a typical same width rolling campaign as example. There are 102 strips in the rolling campaign, p=102. The maximum of shifting stroke is 200 mm, M=200 mm.
Four sets of shifting control parameters are listed in Table 2, and the corresponding shifting strategy is shown in Fig. 3. Four shifting strategies need six steps up to the maximum of shifting stroke. For the shifting strategy with varying stroke, shifting stroke in the end of a rolling campaign is set to be a half of the maximum stroke:
M-M·A·(p-N)=M/2
that is
A=0.5/(p-N)
Table 2 Control parameters of four types of shifting strategy

The corresponding characteristic parameters are shown in Figs. 4 and 5, including cat ear height and gap contour smoothness of all strips.
Figure 4 indicates that the shifting strategy with varying stroke can gain smaller cat ear height than the one with fixed stroke, and the shifting strategy with varying step can gain smaller cat ear height than the one with fixed step. Varying step is more effective than varying stroke in reducing cat ear height.
Figure 5 indicates that the shifting strategy with varying stroke can gain smaller gap contour smoothness than the one with fixed stroke, and the shifting strategy with varying step can gain smaller gap contour smoothness than the one with fixed step. Varying stroke is more effective than varying step in reducing gap contour smoothness.

Fig. 3 Comparison of four types of roll shifting strategy: (a) Shifting strategy with fixed stroke and fixed step; (b) Shifting strategy with varying stroke and fixed step; (c) Shifting strategy with fixed stroke and varying step; (d) Shifting strategy with varying stroke and varying step

Fig. 4 Cat ear height of four types of shifting strategy

Fig. 5 Gap contour smoothness of four types of shifting strategy
Based on the above analyses, it is concluded that both varying stroke and varying step can reduce cat ear height and gap contour smoothness, so the shifting strategy with varying stroke and varying step is better than the one with either varying stroke or varying step.
4 Effect of shifting control parameters on characteristic parameters of roll wear
The cat ear height in the end of a rolling campaign and the average gap contour smoothness of all strips in a rolling campaign can be taken as two evaluation factors to assess the integrated effect of roll shifting strategy on the roll wear. Two evaluation factors are as follows:
 (13)
(13)
 (14)
(14)
The effect of shifting control parameters on two evaluation factors is analyzed to provide the optimal selection of shifting control parameters.
To make good use of shifting stroke, suppose n steps up to the maximum of shifting stroke, where n is the quarter cyclic shifting number. The various shifting steps are gained by the recursive algorithm of shifting strategy, and they are ts, ts+dt, ts+2dt, …, ts+(n-1)dt. Then there is
ts+(ts+dt)+(ts+2dt)+…+ [ts+(n-1)dt]=M
That is
 (15)
(15)
Equation (15) indicates that shifting step increment dt can be converted to quarter cyclic shifting number n.
4.1 Effect of basic shifting step
Set quarter cyclic shifting number to be 6, stroke reduction starting point 30, stroke reduction rate 0.006 9, basic shifting step from 5 mm to 50 mm, and then the effect of basic shifting step on two evaluation factors is gained in Fig. 6. Basic shifting step significantly affects two evaluation factors. With the increase of basic shifting step, cat ear height decreases from 3.3 μm to 2.7 μm, and then increases from 2.7 μm to 4.5 μm. Gap contour smoothness increases linearly from 10.6 μm to 25.4 μm. Figure 6 indicates that two good evaluation factors are gained when basic shifting step is equal to 10 mm.

Fig. 6 Effect of basic shifting step on characteristic parameters
4.2 Effect of quarter cyclic shifting number
Set basic shifting step to be 10 mm, stroke reduction starting point 24, stroke reduction rate 0.006 4, quarter cyclic shifting number from 4 to 8, and then the effect of quarter cyclic shifting number on two evaluation factors is gained in Fig. 7. With the increase of quarter cyclic shifting number, cat ear height sharply decreases from 4.9 μm to 2.7 μm, and then increases from 2.7 μm to 3.8 μm. Gap contour smoothness increases slowly from 9.1 μm to 15.4 μm. Figure 7 indicates that two good evaluation factors are gained when quarter cyclic shifting number is equal to 6.

Fig. 7 Effect of quarter cyclic shifting number on characteristic parameters
4.3 Effect of stroke reduction starting point
Set basic shifting step to be 10 mm, quarter cyclic shifting number 6, stroke reduction rate 0.006 8, stroke reduction starting point from 12 to 52, and then the effect of stroke reduction starting point on two evaluation factors is gained in Fig. 8. With the increase of stroke reduction starting point, cat ear height sharply decreases from 3.7 μm to 2.73 μm, and then slowly increases from

Fig. 8 Effect of stroke reduction starting point on characteristic parameters
2.73 μm to 2.81 μm. Gap contour smoothness increases from 9.8 μm to 13.4 μm. Therefore, two good evaluation factors can be gained when stroke reduction starting point is equal to 24.
4.4 Effect of shifting stroke reduction rate
Set basic shifting step to be 10 mm, quarter cyclic shifting number 6, stroke reduction starting point 24, shifting stroke reduction rate from 0 to 0.007 7, and then the effect of shifting stroke reduction rate on two evaluation factors is gained in Fig. 9. With the increase of stroke reduction rate, cat ear height slowly changes from 2.5 μm to 2.7 μm, and sharply increases from 2.7 μm to 3.9 μm. Gap contour smoothness sharply decreases from 19.8 μm to 12.3 μm, and then slowly decreases from 12.3 μm to 9.7 μm. Therefore, two good evaluation factors can be gained when stroke reduction starting point varies from 0.005 5 to 0.006 3.

Fig. 9 Effect of stroke reduction rate on characteristic parameters
4.5 Optimal selection of shifting control parameters
Combined with simulation analysis of a large number of rolling campaigns, the selection ranges of optimal shifting control parameters are listed in Table 3.
Table 3 Selection range of optimal shifting control parameters

5 Application example and discussion
5.1 Practical example
Take the above rolling campaign as an application case (p=102, M=200 mm). According to the simulation analysis, a set of optimal shifting control parameters are listed as follows: n=6, N=24, ts=10 mm, and A=0.006 4. The corresponding shifting strategy is given in Fig. 10.

Fig. 10 Roll shifting position and quartic loading gap profile
5.2 Application effect
The optimal roll shifting strategy was applied to practical production in a hot strip mill. Strip flatness value stays in the range of (0±35) IU (1 IU=1 mm/ 100 m=10-5), and does not deteriorate in the later rolling stage. Strip edge drop value is less than 30 μm, and the trend keeps steady with the advance of a rolling campaign. Compared with traditional shifting strategy, the optimal shifting strategy with varying stroke and varying step can gain better strip profile and extend rolling length of a rolling campaign.
5.3 Discussion
The relation between quartic loading gap profiles and shifting positions of all strips is analyzed. Gap contour in the contact area is obtained from wear contour of the upper and lower work roll, and the gap contour curve is fitted with the polynomial equation [18]:
 ,
,  (16)
(16)
Get the coefficients a2, a4, and then calculate quartic loading gap profile:
 (17)
(17)
Figure 10 gives the gained quartic loading gap profile, which is related to strip edge wave or composite wave [13]. Figure 10 indicates that quartic loading gap profile significantly increases with the increase of roll shifting positions. Varying stroke makes the maximum of shifting positions in the following phase of a rolling campaign smaller than the one in the initial phase, and varying step makes the most of roll shifting positions distributed around zero. Both of them can reduce the effect of shifting positions on loading gap after roll wear accumulating to a certain extent, and reduce uncontrollable quartic loading gap profiles. Therefore, the shifting strategy with varying stroke and varying step is effective in reducing quartic loading gap profile.
In the on-line control of work roll contour, roll thermal contour can be somehow controlled by conventional means like work roll bending, as thermal contour is smooth enough due to heat exchange between roll body centre and edges. But roll wear is not. To some extent, this work provides some control means for roll wear and reduces some restrictions on rolling schedule.
6 Conclusions
1) A new roll shifting strategy with varying stroke and varying step is presented, and a recursive algorithm of establishing the new shifting strategy is proposed.
2) Characteristic parameters of cat ear height and gap contour smoothness are introduced to assess the effect of shifting strategy on roll wear. Both varying stroke and varying step can reduce cat ear height and gap contour smoothness, so the shifting strategy with varying stroke and varying step is better than the one with either varying stroke or varying step.
3) A case study is conducted to validate the proposed shifting strategy, which can improve strip profile and extend rolling length of a rolling campaign. Analysis indicates that both varying stroke and varying step can reduce uncontrollable quartic loading gap profile.
References
[1] TAKASHI A, YOJI I, TOSHIKI Y. Universal continuous caster-hot strip mill direct rolling process by effective utilization of the unique schedule free rolling operation system [J]. Journal of the Iron and Steel Institute of Japan, 1988, 74(7): 182-189.
[2] MASUDA S, TERAUCHI T, TANIGUCHI I. Hot strip profile and flatness control in schedule free rolling with four-high work roll shift mill [C]// 31st Mechanical Working and Steel Processing Conference. Chicago, 1989: 47-53.
[3] ZHANG Qing-dong, HE An-rui, HUANG Lun-wei, CHEN Xian-lin. Shape control in schedule free hot strip rolling [J]. Iron and Steel, 2001, 36(2): 72-75. (in Chinese)
[4] KONG Xiang-wei. Research on conventional work roll shifting and schedule free rolling [D]. Shenyang: Northeastern University, 2003. (in Chinese)
[5] SHAO Jian. Study on profile and flatness control technology in schedule free rolling [D]. Beijing: University of Science and Technology Beijing, 2008. (in Chinese)
[6] CAO Jian-guo, ZHANG Jie, SONG Ping, SU Yi, Yan TAN-li. ASR technology for controlling profile and flatness of non-oriented electrical steel strip in hot rolling [J]. Iron and Steel, 2006, 41(6): 43-46. (in Chinese)
[7] ANON. Work roll shifting devices fitted to a hot strip mill [J]. Steel Times, 1988, 216(11): 590-594.
[8] KITAHAMA M, YARITA I, ABE H, AWAZUHARA H. Profile control of hot rolled strip by working roll shifting (K-WRS) mill [J]. Iron and Steel Engineer, 1987, 64(11): 34-43.
[9] GINZBURG B V. High-quality steel rolling: Theory and practice [M]. New York: Marcel Dekker, 1993: 405-443.
[10] PARK H D, YI J J, KIM J K, SHIN S C. Development of work roll shifting pattern for schedule free in hot rolling [J]. Research Institute of Industrial Science and Technology (Pohang City) Technical Research Report, 1991, 5(4): 789-801.
[11] ODA T. Advanced technology for schedule free rolling. III. Work roll shift method by prediction of roll profile on hot strip mill [J]. Journal of the Japan Society for Technology of Plasticity, 1995, 36(417): 1151-1156.
[12] XU Ning, LIU Hong-yan, XU Zhi-rang. Investigation of roll shift schedule for WRS mill and rolls deflections [J]. Journal of Anhui Technology of University, 2006(4): 410-412. (in Chinese)
[13] SHAO Jian, HE An-rui, YANG Quan. Varying shifting stroke strategy of work rolls in hot rolling [J]. Journal of University of Science and Technology Beijing, 2011, 33(1): 93-98. (in Chinese)
[14] KONG Xiang-wei, XU Jian-zhong, WANG Guo-dong, LIU Xiang-hua. Optimization shift scheme of SFR realized by adopting flat roll [J]. Journal of Northeastern University: Natural Science, 2002, 23(12): 1166-1169. (in Chinese)
[15] CAO Jian-guo, WEI Gang-cheng, ZHANG Jie, CHEN Xian-lin, ZHOU Yi-zhong. VCR and ASR technology for profile and flatness control in hot strip mills [J]. Journal of Central South University of Technology, 2008, 15(2): 264-270.
[16] SACHS G, LATORRE J V. Roll wear in finishing trains of hot strip mills [J]. Iron and Steel Engineer, 1961, 38(12): 71-92.
[17] JOHN S, SIKDAR S, MUKHOPADHYAY A, PANDIT A. Roll wear prediction model for finishing stands of hot strip mill [J]. Ironmaking and Steelmaking, 2006, 33(2): 169-175.
[18] CHEN Xian-lin. Flatness control in new generation high-tech mills for wide strip rolling [J]. Journal of University of Science and Technology Beijing, 1997, 19(Sl): 1-5. (in Chinese)
(Edited by YANG Bing)
Foundation item: Project(50974039) supported by the National Natural Science Foundation of China
Received date: 2011-05-24; Accepted date: 2011-09-23
Corresponding author: LI Wei-gang, PhD Candidate; Tel: +86-21-26641062; E-mail: liweigang@baosteel.com