J. Cent. South Univ. Technol. (2010) 17: 1376-1382

DOI: 10.1007/s11771-010-0645-7

Deduction and experimental investigation of constitutive relation of liquefaction of saturated sand

WANG Xing-hua(王星华)^{1, 2}, CUI Ke-yu(崔科宇)¹, WANG Zhen-yu(王振宇)^{1, 3}, WANG Mian-chan(王绵昌)²

1. School of Civil and Architectural Engineering, Central South University, Changsha 410075, China;

2. Department of Civil and Environment Engineering, the Penn State University,

University Park, PA, 16802, USA;

3. Tunnel Engineering Group, China Communication Construction Group Company, Beijing 100011, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Abstract: According to the existing problems of liquefaction models of saturated sand that were put forward under dynamic action, on the basis of Handin-Drnevich model, a new calculating model of the dynamic constitutive relation of saturated sand was put forward. The model was based on the basic hypothesis of instantaneous limit balance according to the basic principle that the stress estate is the destroyed condition was not overstepped. The calculated method of increment nonlinear was referenced and combined with the excellence of the model of distributed particles. The process of vibrating liquefaction of saturated sand was divided into some areas. And the phenomena of shearing dilatation and unloading shrink of saturated sand were considered. On above basic a new calculating constitutive relation model was proposed. There are a few parameters in the model. The physical means of the parameters are very evident and quantized. They could be obtained from the dynamic triaxial test in door. The model was contrasted and validated with the results of the dynamic triaxial test in door. The comparison of the results of the dynamic triaxial test in door and the calculating results of the model indicates that all sorts of phenomenon appearing in the process of liquefaction of saturated sand could be more perfectly reflected by the model. Especially at the initial stage of development of pore water pressure and strain of saturated sand, the results of the dynamic triaxial test in door are consistent with the calculated results of the model very much. But there is some difference between the results at the anaphase of development of pore water pressure and strain. On the path of stress, the calculating and experimenting ultimate state surfaces are almost identical.

Key words: sand liquefaction; dynamics; constitutive relation; dynamic triaxial test

1 Introduction

In already existence research, for the models of liquefaction of saturated sand under dynamic force, many different calculating models were formed. Because flow direction and plastic modulus were used in formula of the generalized plasticity model [1-4], the formula is simpler. But the used formula did not have obvious physical means. The physical means of formula of particulate medium model [5-6] are more obvious. The results of the model can be related with experiment phenomena nearly, more affecting factors can be considered. But the formula is more complex.

The obtained constitutive model of sand is fairer through macrocosm combined with microscopic in the structure model [7-8]. The relationships of stress and strain, strength and destruction of saturated sand under cyclic loading were considered in the formula. But there are relative more parameters in the formula, and the calculating process is more complex.

On the basis of the Handin-Drnecivh model [9], according to the basic assumption of theory of transient state ultimate equilibrium, a new calculating model was put forward, calculating method of increment nonlinear model was used and advantages of particulate model were colligated, considering the phenomenon of shear expand and shear reduce of liquefaction process.

2 Basic assumption of theory of transient state ultimate equilibrium

That the states of some temporal saturated sand under action of dynamic loading were revealed with the theory [10-13] of transient state ultimate equilibrium put forward by XIE and ZHANG can be considered to be in one of four states: while increasing loading, shear reduces and shear expands; unloading spring back and reverse shear reduce, while its state of static stress and water pressure of void is developed in some processes.

During action of dynamic loading, the four states will occur by turn in some sure law. The change of state is consanguineous relationship with the change of effective stress. In the space of effective stress there are four property spheres reflecting characteristic of four states of matter. The change of the four property spheres to the best of its abilities is reflected with the model. At the same time, medium sand or dense sand under monotone loading or periodic vibration force will be liquefied and after strain-softening, and a steady residual strength is finally attained, as shown in Figs.1 and 2. At the same time, during different vibrational times, the amplitude of pore water pressure of sand will be increased no longer and stress paths will be overlapped each other. But the strain amplitude will be increased in a permanent speed continually. The property of sand was considered in the model used in this work. After entering steady stage residual pore will be increased no longer. This means that body strain of sand is almost elastic, and continual development of axial strain is the result of shearing strain of sand.

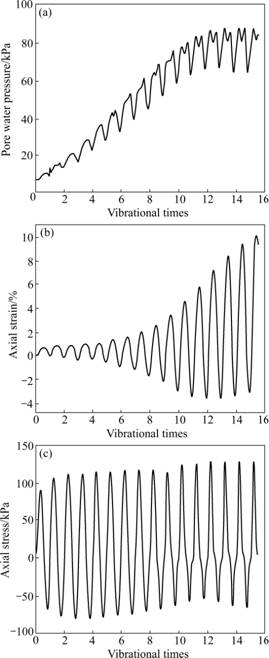
Fig.1 Time travel curve of liquefaction of sand obtained by experiment: (a) Pore water pressure; (b) Axial strain; (c) Axial stress

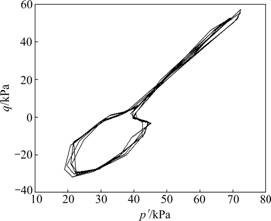
Fig.2 The 30th-35th times vibrational stress path of entering steady stage (p′ is 1/2 of effective volumetric stress; and q is generalized shearing stress)

3 Composite structure model

3.1 Derivation principle

Derivation principles used are as follows:

(1) Destroying condition of sand cannot be exceeded by stress state.

(2) Pore water pressure and shear modulus will be calculated in different region separates.

(3) The value of modulus will be related with effective stress state and property of sand.

(4) The strain will be divided into elasticity part and plasticity part.

3.2 Derivation of composite structure model

The generated plastic deformation of saturated sand under dynamic loading can be divided into two parts: 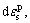 plastic deformation due to change of shear stress and  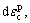plastic deformation due to increase of consolidating pressure, i.e.

                             (1)

It is supposed that the plastic deformation due to increase of consolidating pressure is isotropy and shearing strain will not be developed.

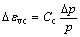                               (2)

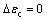                                    (3)

where C_c is the initial damping ratio, C_c=0.434λ₀; λ₀ is an experiment parameter; ?ε_vc is the volumetric strain magnitude; ?p is the difference of effective body stress; p is the effective body stress; and ε_c is the plastic deformation.

It is indicated that under condition that generalized shearing stress is constant, rotation of axis of principal stress will be brought to change of volumetric strain. But what the relationship between generalized shearing stress and generalized shearing strain is used cannot be reflection of affecting of rotation of axis of principal stress on volumetric strain. For the effect, according to Ref.[14], dγ, generalized deviator strain, is:

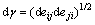                             (4)

where e_ij is the deviate strain.

Hence, equation of backbone curve can be obtained:

            (5)

where

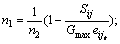
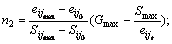
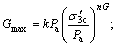
S_i is the deviator stress tensor; S_ij0 and e_ij0 are the deviator stress and deviator strain on the turning point of the curve, respectively; 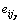is the reference deviator strain, 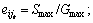G_max is the initial shearing modulus of circular; n₁ and n₂ are the model parameters; and k is the consolidation ratio.

Differentiating deviator strain of formula (5) yields

               (6)

where

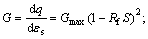
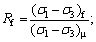
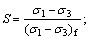
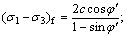
ε_s is the plastic strain; q is the generalized shearing stress; R_f is the damaging stress ratio; S is the stress; (σ₁-σ₃)_f=

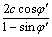 represents Mohr-Coulomb law; σ₁ and σ₃ are

the maximum and minimum main stresses, respectively; and φ′ is the effective inside friction angle.

Because of increase of pore water pressure and decrease of effective confining pressure, degradation of sand will occur to. Changing trend of shear strain can be reflected from change of G_max. Fig.3 shows that vibration amplitude of axis strain will be increased with the increase of vibration time, and the sharp of hysteresis loop will not be an ellipse anymore. Fig.4 shows that the shear dynamical modulus will be degraded with increasing vibration time. In Fig.4, ε is remnants strain, and ε_L is the axis strain when the saturated sand is destroyed.

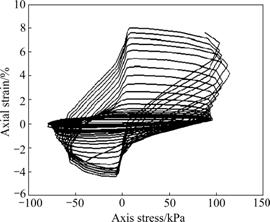
Fig.3 Hysteresis loop of strain vs stress from experiment

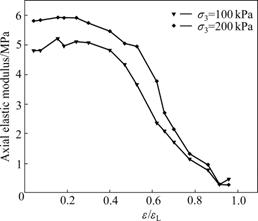
Fig.4 Process of degradation of shear dynamical modulus of sand

During the vibration liquefaction of sand, formula (4) should be satisfied at one time:

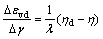                            (7)

where

;

;

;

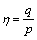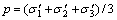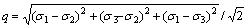?ε_vd is the volume strain of sand; and η_d is equal to η when the entering shearing expanding.

Then:

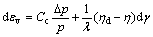                    (8)

The strain is divided into two parts: elasticity and plasticity. And according to that volume strain becomes elasticity gradually during vibration liquefaction, the formula is:

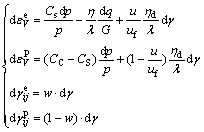             (9)

where

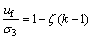                            (10)

w is the weight parameter of elastoplastic of generalized shear strain. It is thought usually that w is related with state in that vibration of sand is. At the early state of vibration, w will be more value, and at the anaphase of vibration w will be less value. In this paper w is 0.8. u_f is the limit pore water pressure of sand. It can be obtained from experiment. ζ is the relation with characters of sand. 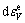 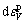and  are the volume deformation produced by pore water pressure and consolidation stress, separately.  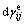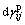and  are the generalized deviator strains produced by pore water pressure and consolidation stress, separately. C_s=0.434 k₀, k₀ is the experimental parameter.

When the stress path is in limit state, then

                               (11)

where

;

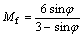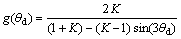               (12)

M_f is the slope of destroy line of triaxial compress experiment; g(θ_d) [15]; and θ_d is the function of Lode angle. It decides shape of failure surface on the π surface [16-17]. K is the strength ratio of triaxial extension to triaxial compression. For the Mohr-Coulomb material, there exists

.

Here stress path of sand will be moved along limit state surface, so volume strain is equal to 0, which can calculated according to the following formulas:

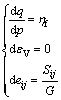                                 (13)

It is clear that whole vibration liquefaction process is divided into many areas by formula (13). It can be reflected a set of phenomena of shearing dilatation, shearing shrinkage, stiffness degradation and unloaded volume shrinkage.

4 Numerical expression of constitutive model

The strain can be written as

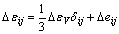                        (14)

The relationship between stress and strain can be written as follows:

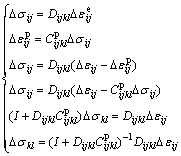               (15)

Formula (15) is the constitutive model put forward in this work.

At the same time, under the condition of no-drainage, slippage between two sand grains will be caused by the vibration force. The volume strain of sand will be also caused by the slippage. It will necessarily lead to the increase of a part of force between grains transferred to water and pore water pressure and the decrease of effective stress. It will also cause that restorable volume strain that is stored in sand grains in form of elastic deformation will be released. Because of condition of volume compatibility, the result of circus is: the change of pore volume is equal to the change of net volume of sand structural. If the change of water volume is ignored, the following equation can be obtained according to the compatibility condition:

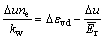                          (16)

where k_w is the modulus of volume change of pore water; n_e is the porosity; ?u is the increment of pore water pressure; and 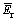 is the tangent modulus of one dimensional unloaded curve of sand.

If volume change of pore water is ignored, the following equation can be obtained:

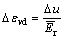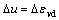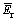or ×                (17)

5 Confirming parameters of constitutive model

It can be considered approximatively that static frictional angel of sand is equal to dynamical frictional angel of the sand [18]. The dynamical frictional angel of sand can be obtained by general triaxial experiment. The modulus of volume compression and the modulus of resilience of sand can be obtained by homogeneous compression experiment [14], then

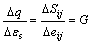                            (18)

Using shearing experiment that spherical stress is constant (p=constant), the relationship curve of generalized shearing force q and generalized shearing strain ε_s can be obtained. The curve is a hyperbola curve, i.e. the curve is a backbone curve of Hardin-Drnevich model shown by the experiment:

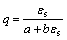                                (19)

where a is the slope of initial tangent of q-ε_s curve; and b is the reciprocal of asymptotic value of main stress difference.

η_d, a parameter of shearing dilation, is the stress ratio when sand starts shearing expanding correspondingly.

It can be obtained by observing increasing time-history curve of pore water pressure. When the curve of pore water pressure appears on the first steady flute, sand is entered into state transform surface, and volume expanding produced by shearing dilation is more than volume compression produced by volume stress, which generally leads to shearing dilation and the decrease of pore water pressure. It can be considered approximatively that stress ratio will be η_d at this time.

6 Model confirmation

For validating correctness of the modal (formula (15)), the test was carried out indoor experiment using dynamical triaxial tester. DDS-70 dynamical triaxial tester controlled by microprocessor was used in the test. The experiment process can be real-time watched by the apparatus. And the experimental data of axial force, strain and pore pressure, etc. during experiment could be recorded and stored. Sand sample used in the experiment was from Dongtinghu Lake, Hunan Province, China. Its main parameters are shown in Tables 1 and 2.

According to the dynamic balance equation of soil framework founded with saturated porous medium theory and considering seepage and effective stress principle, after above model (formula (15)) was substituted, testing calculation can be carried out through immediately. The division of cell of sand sample is shown in Fig.5. The used model is an axisymmetric model. The comparison and analysis of results of indoor experiment and results of model calculation are shown in Figs.6-10.

Figs.6 and 7 show that at the initial phase of development of pore water pressure and strain of sand, the results of calculation are closer to the results of experiment because sand is in the no-linear state at the phase, and the simulation of model is more exact. After entering into shearing dilation phase, the accuracy of simulation of the model to development of pore water pressure will be decreased, the calculated value of pore pressure is less than experimental value. Calculation of shearing dilation using the model is large, but the calculated result of strain of sand is still more perfect. During anaphase of the experiment, the result of calculation of the model is the same to the result of experiment at the limit pore water pressure. But there is more windage of simulation of model for strain. There are two reasons: at first, the result that yield process of limit state surface of sand is simulated by the model is not still perfect, and that the value of the parameters can be obtained nicely is still difficult. Second, after sand is pulled and destroyed in the experiment, dynamical loading cannot be appended on sand in total. It is different from that during calculation the amplitude of dynamical loading is kept to be constant.

Table 1 Parameter of sand

Table 2 Composition grain of sand

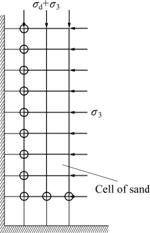
Fig.5 Division of sand cell

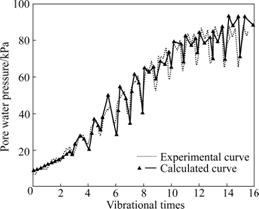
Fig.6 Comparison of calculated pore pressure and experimental pore pressure

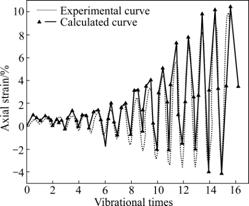
Fig.7 Comparison of calculated strain and experimental strain

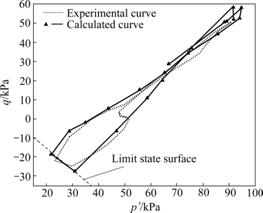
Fig.8 Comparison of calculated stress path and experimental stress path

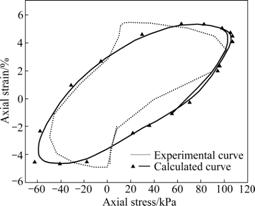
Fig.9 Comparison of calculated hysteresis loop and experimental hysteresis loop

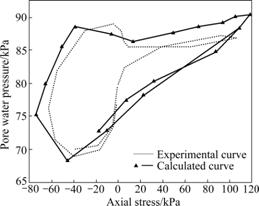
Fig.10 Comparison of calculated pore pressure and experimental pore pressure

Fig.8 shows that both limit state surfaces of stress paths of calculation and experiment are almost concordant.

In Fig.9, the calculated hysteresis loop is in the shape of an ellipse approximately, but the experimental hysteresis loop is in an abnormity form. The main reason is: during experiment, after sand is pulled and destroyed, dynamical loading can be appended on the sand in total, but during calculation the amplitude of dynamical loading is still kept to be constant. The reason that there is a phenomenon of “un-loading and increasing pressure” in Fig.10 is the same.

Fig. 10 shows that for the relationship between pore water pressure and axial pressure, difference of results of calculation and experiment is also reflected on the phenomenon of “un-loading and increasing pressure”. But while axial tensile stress is more unloaded, in experiment, pore water pressure will be zoomed, but the pressure is increased in gentle in calculation.

From above it is known that the model can present more perfectly all kinds of phenomena appearing in process of liquefaction of sand, especially for pore water pressure, initial phase of strain development and limit state surface of stress path, the results of calculation well agree with results of experiment.

7 Conclusions

(1) On the basis of Handin-Drnevich model, a new calculative constitutive model that is simple for calculation is educed. The model is validated with indoor dynamic triaxial tests. All kinds of phenomena appearing during liquefaction of sand can present more perfectly by the model. But there are some differences between the results of experiment and those of calculation. The model is not perfect. There are still some bugs in the model.

(2) At the initial phase of development of pore water pressure and strain of sand, the results of calculation of the model are nearer the results of experiment.

(3) The calculated hysteresis loop of the model is in the shape of an ellipse approximately, but the experimental hysteresis loop is in an abnormity form.

(4) For the relationship between pore water pressure and axial pressure, difference of results of calculation and experiment also reflects the phenomenon of “un-loading and increasing pressure”.

References

[1] MROZ Z, ZIENKIEWICS O C. An anisotropic critical state model for soils subjected to cyclic loading [J]. Geotechnique, 1981, 31(4): 451-470.

[2] PASTOR M, ZIENKIEWICS O C, CHEN H C. Generalized plasticity and modeling of soil behavior [J]. Inter Tran of Nume Anal Methods in Geotechnics, 1990(2): 151-190.

[3] ZHANG Jian-min, WANG Gang. Mechanism of large post-liquefaction deformation in saturated sand [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(7): 33-38. (in Chinese)

[4] WANG Gang, ZHANG Jian-min. Numerical modeling of liquefaction-induced deformation in sand [J]. Chinese Journal of Geotechnical Engineering, 2007, 29(3): 96-102. (in Chinese)

[5] SHEN Zhu-jiang. A granular medium model for liquefaction analysis of sands [J]. Chinese Journal of Geotechnical Engineering, 1999, 21(6): 742-748. (in Chinese)

[6] WANG Gang, ZHANG Jian-min. Recent advances in seismic liquefaction research [J]. Advances in Mechanics, 2007(4): 97-111. (in Chinese)

[7] SHEN Zhu-jiang. Critical review and reconstitution of constitutive theory of sands [C]// The 6th Conference of Numerical Analysis and Analytic Method of Soil Mechanics. Guangzhou: Guangdong Press of Science and Technology, 1998: 16-23. (in Chinese)

[8] GUO Sheng-bing, WANG Ming-yang, QIAN Qi-hu. Study on characteristics of explosion liquefaction of saturated sandy soil [J]. Rock and Soil Mechanics, 2007, 28(3): 427-435. (in Chinese)

[9] CARTER J P, BOOKER J R, WROTHU C P. A critical state soil model for cyclic loading [C]// PANDE G N, ZIENKIEWICS O C, eds. Soil Mechanics-Transient and Cyclic Loadings. London: John Wiley and Son, 1982: 35-62.

[10] XIE Ding-yi, ZHANG Jian-ming. Research on transient change mechanism of pore water pressure in saturated sand under cyclic loading [J]. China Civil Engineering Journal, 1990, 23(2): 51-60. (in Chinese)

[11] LIU Yang, ZHOU Jian, FU Jian-xin. Fluid-particle coupled model for saturated sand and its application to liquefaction analysis [J]. Journal of Hydraulic Engineering, 2009, 40(2): 250-256. (in Chinese)

[12] ZHOU Jian, YANG Yong-xiang, LIU Yang. Model testing of meso-fabric of saturated sand liquefaction [J]. Journal of Tongji University: Natural Science, 2009, 37(4): 466-470. (in Chinese)

[13] WANG Yan-li, WANG Yong. Experimental study on evolutionary characteristics of dynamic pore water pressure of saturated sands [J]. Journal of Tongji University: Natural Science, 2009, 37(12): 1603-1607. (in Chinese)

[14] SHAO Sheng-jun, XIE Ding-yi. Research on dynamic behaviours and its application approach of saturated sands [J]. Journal of Xi’an University of Technology, 1999, 15(3): 34-38. (in Chinese)

[15] QIU Chang-lin, YAN Shu-wang. A universal elastoplastic model of saturated sands under cyclic loading [J]. Journal of Hydraulic Engineering, 1998(12): 42-46. (in Chinese)

[16] FENG Tu-gen, LIU Han-long, GAO Yu-feng, FEI Kang. Seismic response characteristic of horizontal layer [J]. Journal of PLA University of Science and Technology: Natural Science Edition, 2009, 10(S1): 74-79. (in Chinese)

[17] LI Jin-kun, ZHANG Qing-hui. The effects of lode’s angle of stress on pore pressure development [J]. Chinese Journal of Geotechnical Engineering, 1994, 16(7): 17-21. (in Chinese)

[18] WU De-lun, ZHANG Jian-hua. A weighted absorbing boundary for wave propagation in porous elastic media [J]. Journal of Hydraulic Engineering, 1997, 19(4): 57-63. (in Chinese)

(Edited by YANG You-ping)

Foundation item: Project(59979001) supported by the National Natural Science Foundation of China

Received date: 2010-03-05; Accepted date: 2010-05-20

Corresponding author: WANG Xing-hua, PhD, Professor; Tel: +86-731-82655489; E-mail: xhwang@mail.csu.edu.cn