机器激励下考虑填充墙影响的结构动力响应分析

李敏锋¹，金国芳¹，李永华²

(1. 同济大学 结构工程与防灾研究所，上海，200092；

2. 南昌大学 建筑工程学院，江西 南昌，330031)

摘要：为了研究在机器激励下填充墙对结构动力响应的影响，根据现场实测结果，从时域上利用Newmak法对该结构进行动力时程分析；基于实测数据的功率谱，拟合出Kanai-Tajimi模型的参数，利用SAP2000的PSD分析模块对结构进行随机振动分析，与未考虑填充墙影响时结构的动力响应进行分析比较。研究结果表明：考虑填充墙影响后，结构的自振频率增大，与实测结构频率及机器工作频率更接近；考虑填充墙影响后，结构的加速度、速度以及内力响应均增大，位移响应因结构的共振效应也增大。

关键词：钢筋混凝土剪力墙结构；填充墙；机器激励；时程分析；随机振动分析；动力响应

中图分类号：TU375       文献标志码：A         文章编号：1672-7207(2013)05-2041-06

Dynamic response analysis of infilled shear wall structure under machine excitation

LI Minfeng¹, JIN Guofang¹, LI Yonghua²

(1. Research Institute of Structural Engineering and Disaster Reduction, Tongji University, Shanghai 200092, China;

2. School of Civil Engineering and Architecture, Nanchang University, Nanchang 330031, China)

Abstract: The dynamic response analysis of infilled shear wall structure under machine excitation was studied. Based on the tested results, the dynamic time history analysis using Newmark method was applied. Based on the power spectrum density (PSD) of tesed data, parameters of Kanai-Tajimi modal were fitted. Using the PSD analysis of SAP2000, the random vinration analysis was carried out, and the response results were compared to those of the structure without infill wall. The results show that the natural frequency of infilled shear wall structure increases, and is close to the tested frequency and machines’ working frequency. The acceleration, velocity, displacement and internal force responses all increase.

Key words: RC shear-wall structure; infill wall; machine excitation; time history analysis; random vibration analysis; dynamic response

在建设工程中的各种振源如打桩机、重锤以及工业生产中的机械设备如锯石机、冲压机床设备往往由于其振动的频率与结构的固有频率接近，引起房屋振动。这类机器激励致使房屋振动与地震动相似，均通过基础传递到上部结构，但持续时间比地震长。国内外学者对于考虑填充墙的钢筋混凝土框架结构抗侧体系进行了大量研究，并取得了一定的成果^[1-5]。但对于考虑填充墙的剪力墙结构特别是短肢剪力墙结构方面的研究甚少。由于填充墙抗侧刚度相对剪力墙结构的抗侧刚度较小，计算中很容易忽略填充墙刚度的贡献.事实上，在很多短肢剪力墙结构体系高层住宅房屋中，填充墙的作用不容忽视。我国规范^[6]对剪力墙结构的周期折减系数取0.8~1.0，对短肢剪力墙结构体系，填充墙的影响作用较大，取0.8，但都没有考虑填充墙刚度的贡献。Metin等^[7]利用SAP2000建立1幢考虑填充墙影响的10层高层建筑三维空间模型，采用对角斜杆模拟填充墙，分析结构在地震作用下的响应。李敏锋等^[8]对考虑填充墙的单层双肢剪力墙的抗侧刚度进行了分析，建议在弹性阶段可采用整体墙元模型来计算考虑填充墙的剪力墙结构体系。Li等^[9]则对某剪力墙结构在机器激励下的振动响应进行了测试和分析，但计算模型中没有考虑填充墙刚度的贡献。本文作者基于文献[9]中的具体工程实例，根据现场实测的振动结果，对考虑填充墙影响时结构的动力特性和动力响应进行分析，与未考虑填充墙时进行比较。结合现场实测响应，对2种情况下的计算结果进行对比分析，以便为类似振动问题和工程振动分析提供参考。

1  计算模型及运动方程

1.1  计算模型

根据设计图纸，房屋采用桩基础，剪力墙墙厚地下室为250 mm，其余各层均为200 mm。梁的主要截面长×宽分别为200 mm×250 mm，200 mm×300 mm，200 mm×350 mm及200 mm×400 mm。钢筋混凝土楼板板厚为110 mm，局部为150 mm及90 mm。建立考虑剪力墙刚度贡献的SAP2000有限元模型，剪力墙、填充墙、楼板采用薄壳单元，梁柱采用杆系单元，当连梁的跨高比大于5时按梁进行模拟，对连梁刚度予以折减。现场调查未发现填充墙开裂现象，结构基本处于弹性状态，因此，建立空间整体墙元模型^[8]，如图1所示。当填充墙开洞较大且两端均无剪力墙或约束时，不考虑填充墙刚度的影响。

图1  计算模型

Fig.1  Calculation modal

混凝土强度等级为C30，弹性模量为3.0×10¹⁰ Pa，泊松比为0.2，混凝土小型空心砌块的弹性模量为2.562×10⁹ Pa，泊松比为0.15。

1.2  运动方程

对于多自由度体系，其运动方程^[10]可表示为

         (1)

式中：M，C和K分别为结构质量刚度矩阵、阻尼矩阵、刚度矩阵；，，和分别为加速度、速度、位移以及输入加速度激励向量。阻尼矩阵采用瑞利阻尼计算，比例系数通过结构的前2阶自振频率求解。输入激励是复杂的随机函数，采用现场实测结果进行计算。

2  动力特性分析

根据建立的有限元模型，计算结构的前3阶自振周期与不考虑填充墙刚度贡献时的结构前3阶自振周期对比如表1所示。

表1  结构动力特性计算结果对比

Table 1  Comparison of structural dynamic property

由表1可知：考虑填充墙刚度影响后结构的自振频率明显增大，与实测结构自振频率x向差别较大。这主要是x向的门窗开洞较大以及两端无约束填充墙的刚度对结构刚度的贡献没有考虑，但y向的自振频率非常接近。考虑填充墙刚度贡献后结构的振型规律基本一致，第1阶振型为x向平动，第2阶振型为y向平动，第3阶振型为扭转，因此，可以确定机器激励引起了结构的“晃动”。

3  动力响应分析

对考虑填充墙影响的剪力墙结构进行时程分析以及频域上的随机振动分析，并与未考虑填充墙影响时结构的响应进行对比。

3.1  动力时程分析

在机器激励下，结构处于弹性状态，采用Newmark法(γ=1/2，β=1/4)求解运动方程。输入现场地下室实测的加速度激励如图2所示(其中，1g=9.8 m/s²)，计算考虑填充墙与不考虑填充墙时各楼层的水平绝对加速度峰值与实测峰值，如图3所示。

图2  输入加速度激励

Fig. 2  Input acceleration excitation

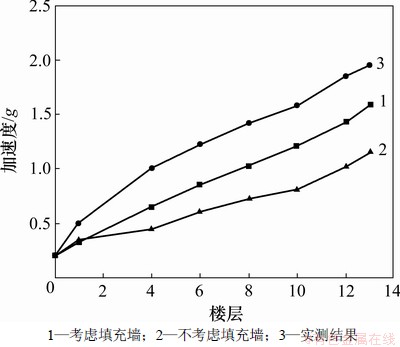
图3  各楼层的水平绝对加速度峰值分布

Fig. 3  Absolute peak acceleration distribution of floor

从图3可知：考虑填充墙和不考虑填充墙的计算结果与实测结果有一定误差，但显然考虑填充墙后的误差比未考虑填充墙时的要小。而这种误差可能是测试时的噪声以及风振所所致。

顶层水平向考虑填充墙与不考虑填充墙时结构的动力反应如图4和图5所示。

图4  顶层x向绝对加速度

Fig.4  Absolute acceleration of top floor in x direction

图5  顶层y向绝对加速度分布

Fig.5  Absolute acceleration of top floor in y direction

从图4和图5可以看出：无论考虑填充墙与否，x向绝对加速度实测值与计算值均有偏差，且峰值与实测值比较接近；不考虑填充墙时，y向绝对加速度计算值与实测值有一定峰值偏差及时滞；而考虑填充墙后，计算结果与实测值非常接近，数值模拟效果较好。

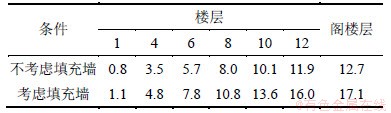
由于结构的水平y向振动比较明显，因而，计算结构的各层水平y向相对位移，见表2。表2中结构的水平相对位移并没有因为考虑填充墙后结构的抗侧刚度增大而减小，相反，其y向水平相对位移有所增大。不考虑填充墙时，各楼层y向最大水平相对位移为12.7 mm，而考虑填充墙后，y向最大水平相对位移可以达到17.1 mm。这主要是考虑填充墙后，结构的自振频率更接近机器正常工作频率而产生的共振效应所致。

表2  y向水平相对位移对比

Table 2  comparison of structural dynamic property in y direction        mm

3.2  随机振动分析

3.2.1  随机功率谱模型及参数

大型机器激励引起的地面运动在传播过程中需要经过土层来传播，传播方式与地震波的相似，从房屋基础传递到上部结构，所以，本文采用地震动随机模型近似模拟。根据现场实测地面加速度记录样本，采用最小二乘法拟合随机功率谱模型参数。选取最经典且在实际工程中应用最广泛的Kanai-Tajimi模型^[11](简称K-T模型)：

    (2)

并选取胡聿贤等^[12]改进的Kanai-Tajimi模型

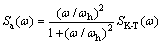         (3)

进行对比。其中：和分别为输入Kanai- Tajimi及改进的Kanai-Tajimi加速度功率谱函数。由于该房屋所在地场地土类别为Ⅳ类土，地震设计分组为第1组，采用现行抗震设计规范规定的特征周期求出地表土层的卓越频率，以及欧进萍等^[13]给出的模型参数阻尼分别为ω_g=9.67 rad/s，ξ_g=0.90。胡聿贤等^[12]模型中反映基岩特性的谱参数ω_h=2.0 rad/s。地面加速度最大值的均值取5 cm/s²，谱强度因子S₀采用薛素铎等^[14]给出的具体参数计算出S₀=0.140 39 cm²/s³。

现场实测机器激励下的加速度功率谱如图6所示，根据最小二乘法可以拟合出模型参数卓越频率为ω_g=12.14 rad/s，阻尼比ξ_g=0.60。

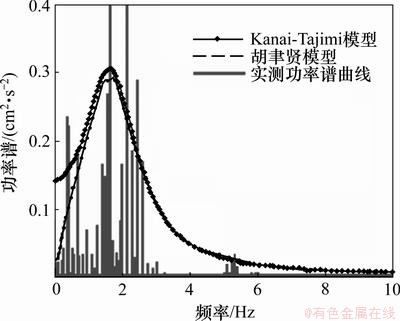
图6  输入随机功率谱曲线

Fig.6  Curves of input PSD modal

3.2.2  线性平稳随机响应分析

对于多自由度线性平稳随机振动分析，可以利用SAP2000提供的PSD分析模块进行分析。输入响应功率谱与输入功率谱间的关系为^[15]

     (4)

其中：；为振型向量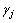；为振型参与系数；为加速度功率谱。根据结构的质量、阻尼以及刚度可以计算出频响函数，由于输入功率谱密度已知，从而可根据式(4)计算结构的输出响应。

根据拟合的参数，代入功率谱模型作为输入PSD函数。利用SAP2000求出考虑顶填充墙与不考虑填充墙时结构顶层y向绝对加速度、相对速度、相对位移以及基底剪力和弯矩峰值对比结果如表3所示。

表3  y向功率谱峰值对比

Table 3  Comparison of PSD peak in y direction

从表3可知：考虑填充墙后，顶层绝对加速度、相对速度和相对位移功率谱响应有所增大，且绝对加速度增大的幅度较明显；基底剪力和弯矩功率谱响应均有所增大，且剪力功率谱响应增大幅度较明显。

进一步研究响应曲线在频域上的分布，得到顶层y向的绝对加速度、相对位移功率谱响应曲线对比结果分别如图7和图8所示，基底剪力和基底弯矩的功率谱响应分布分别如图9和图10所示。考虑到胡聿贤模型与K-T模型响应曲线基本相同，且峰值相对接近，为了在图中能更清晰地比较，各图中对比了K-T模型和实测功率谱模型的结果。

由图7~10可知：考虑填充墙后峰值对应的频率增大，由于考虑填充墙后结构的刚度增大，从而频率增大；且无论是变形还是内力功率谱响应，其能量集中分布在结构自振频率附近。

图7  绝对加速度响应曲线图

Fig.7  Response curves of absolute acceleration

图8  相对位移响应曲线

Fig.8  Response curves of relative displacement

图9  基底剪力F_y响应曲线图

Fig.9  Response curves of base shear F_y

图10  基底弯矩M_x响应曲线

Fig.10  Response curves of base moment M_x

4  结论

(1) 对剪力墙结构进行振动分析时，应考虑填充墙的影响；考虑填充墙后结构的自振频率有所增大，与实测值更接近，因而能引起房屋共振。

(2) 不考虑填充墙时绝对加速度计算值与实测值有一定峰值偏差及时滞；而考虑填充墙时，绝对加速度计算结果与实测值接近，模拟效果较好。

(3) 考虑填充墙后，结构的水平相对位移并没有因为考虑填充墙刚度后结构的抗侧刚度增大而减小，相反，结构的水平相对位移因结构的共振效应而有所增大。

(4) 自振频率处结构的响应最大，且K-T模型和胡聿贤模型计算结果接近，比实测功率谱模型的峰值略高；考虑填充墙后，顶层绝对加速度、相对速度、基底剪力和弯矩功率谱响应均有所增大，而相对位移功率谱响应因结构共振效应也增大。

参考文献：

[1] Stafford S B. Behavior of square infilled frames[J]. Journal of Structural Engineering (ASCE), 1966, 92(1): 381-403.

[2] Liauw T C, Kwan K H. Unified plastic analysis for infilled frames[J]. Journal of Structural Engineering (ASCE), 1985, 111(7): 1427-1448.

[3] Thiruvengadam V. On the natural frequencies of infilled frames[J]. Earthquake Engineering and Structural Dynamics, 1985, 13(4): 401-419.

[4] Asteris P G. Lateral stiffness of brick masonry infilled plane frames[J]. Journal of Structural Engineering (ASCE), 2003, 129(8): 1071-1079.

[5] 童岳生, 钱国芳, 梁兴文, 等. 砖填充墙钢筋混凝土框架的刚度及其应用[J]. 西安冶金建筑学院学报, 1985, 44(4): 21-35.

TONG Yuesheng, QIAN Guofang, LIANG Xingwen, et al. The stiffness of infilled reinforced concrete frame and its application[J]. Journal of Xi’an Institute of Metallurgy and Construction Engineering, 1985, 44(4): 21-35.

[6] JGJ 3—2010, 高层建筑混凝土结构技术规程[S].

JGJ 3—2010, Technical specification for concrete structures of tall building [S].

[7] Metin K K, Ozge K. Effects of infill walls on base responses and roof drift of reinforced concrete buildings under time-history loading[J]. The Structural Design of Tall and Special Buildings, 2011, 20(3): 402-417.

[8] 李敏锋, 金国芳. 单层双肢剪力墙结构弹性抗侧刚度分析[J]. 结构工程师, 2012, 28(1): 8-13.

LI Minfeng, JIN Guofang. Elastic lateral stiffness of single-story coupled shear walls[J]. Structural Engineers, 2012, 28(1): 8-13.

[9] LI Minfeng, JIN Guofang. Vibration source inversion and vibration evaluation of a tall residential building[J]. Advances in Civil Engineering, AMR, 2011, 255/260: 1770-1774.

[10] Clough R, Penzien J. Dynamics of structures[M]. 3rd ed. New York: McGraw-Hill, 2003: 173.

[11] Kanai K. Semi-empirical formula for the seismic characteristics of the ground motion[J]. Bulletin of the Earthquake Research Institute, 1957, 35(2): 308-325.

[12] 胡聿贤, 周锡元. 弹性体系在平稳和平稳化地面运动下的反应[C]//中国科学院土木建筑研究所地震工程研究报告集(第1集). 北京: 科学出版社, 1962: 33-50.

HU Yuxian, ZHOU Xiyuan. The response of the elastic system under the stationary and nonstationary ground motions[C]// Earthquake Engineering Research Report (No.1) by the Institute of Civil Engineering, Chinese Academy of Sciences. Beijing: Science Press, 1962: 33-55.

[13] 欧进萍, 牛荻涛, 杜修力. 设计用随机地震动的模型及其参数确定[J]. 地震工程与工程振动, 1991, 11(3): 45-54.

OU Jinping, NIU Ditao, DU Xiuli. Model and parameters of random ground motion to design[J]. Journal of Earthquake Engineering and Engineering Vibration, 1991, 11(3): 45-54.

[14] 薛素铎, 王雪生, 曹资. 基于新抗震规范的地震动随机模型参数研究[J]. 土木工程学报, 2003, 36(5): 5-10.

XUE Suduo, WANG Xuesheng, CAO Zi. Parameters study on seismic random model based on new seismic code[J]. China Civil Engineering Journal, 2003, 36(5): 5-10.

[15] 俞载道, 曹国敖. 随机振动理论及其应用[M]. 上海: 同济大学出版社, 1988: 106.

YU Zaidao, CAO Guoao. Theory of random vibration and application[M]. Shanghai: Tongji University Press, 1988: 106.

(编辑  陈灿华)

收稿日期：2012-04-08；修回日期：2012-07-05

基金项目：国家自然科学基金资助项目(51168037)

通信作者：李敏锋(1983-)，男，江西新余人，博士研究生，从事工程抗震、结构鉴定与加固研究；电话：13564974942；E-mail: liminfeng001@163.com