J. Cent. South Univ. Technol. (2009) 16: 0177-0183
DOI: 10.1007/s11771-009-0030-6 
First-principles lattice stability of Fe, Ru and Os
TAO Hui-jin(陶辉锦)1, 2, 3, YIN Jian(尹 健)3
(1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;
2. School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China;
3. Key Laboratory of Nonferrous Materials Science and Engineering, Ministry of Education,
Central South University, Changsha 410083, China)
Abstract: Lattice constants, total energies and densities of states of transition metals Fe, Ru and Os with BCC, FCC and HCP structures were calculated by the GGA+PBE functional and the ultrasoft pseudo-potential plane wave method, and compared with those of the first-principles projector augmented wave (PAW) method, CALPHAD method and experimental data. The results show that the lattice stability of this work is ?GBCC-HCP>?GFCC-HCP>0, agreeing well with those of PAW method in the first-principles and CALPHAD method except for BCC-Fe. And the densities of state of HCP-Ru and Os have an obvious character of stable phase, agreeing completely with the results of the total energy calculations. Further analyses of atomic population show that the transition rate of electrons from s to p state for HCP, FCC and BCC crystals increases from Fe to Os, and a stronger cohesion, a higher cohesive energy or a more stable lattice between atoms of heavier metals are formed.
Key words: Fe; Ru; Os; lattice stability; first-principles
1 Introduction
The lowest and the most basic system of phase diagrams is the unary system, i.e. the pure elements, and the assessment of relative Gibbs energy between different crystalline structures of pure elements, i.e. the lattice stability parameters, is the most important foundation of CALPHAD [1]. Scientific Group Thermodata Europe (SGTE) [2] has established Gibbs energy functions of different structures for 78 kinds of elements above 298.15 K. At the same time, the first-principles methods can be used to calculate total energies, electronic densities of state and other properties from the perspective of quantum mechanics [3]. Such thermodynamic properties as cohesive energy, heat of formation and heat of phase transition can be calculated by first-principles method as well [4-11]. More importantly, the physical reason of lattice or phase stabilities of materials can be further understood according to the total energy and electronic structure calculations [12-16]. Recently, systematic calculations of lattice stability have been performed for all the transition and simple metals [17], and even the lattice stabilities of some intermetallics or alloys have been studied as well [18-19].
To find the difference between CALPHAD and the first-principles and explore the physical reason of lattice stability of pure metals, elements Fe, Ru, Os in ⅧB group were selected for calculations in pseudo-potential plane wave method of the first-principles [20]. And the generalized gradient approximation (GGA) [21] was used to calculate the total energies, lattice constants and densities of state for these elements. All the results were compared with the experimental data.
2 Principles and methods
2.1 First-principles
The first-principles are based on the density functional theory. It is completely an ab-initio theory based on quantum mechanics [22]. And it is the Schr?dinger equation of the system of many particles
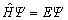 (1)
(1)
that describes materials. In principle, all the possible information is included in the wave function of many particles, and all the physical quantities can be calculated by the strict solution of Schr?dinger equation. But in fact, the solutions can only be calculated with some reasonable approximations due to the complexity of real material system. As the elementary approximation, three hypotheses are introduced to simplify this problem: (1) using the non-relative approximation to solve the non-relative Schr?dinger equation instead of the relative Dirac equation; (2) using the Born-Oppenheim approximation to separate the Schr?dinger equation of the system respectively into the equations of nuclei and electrons; (3) using the single-electron approximation to transform the multi-electron equation into the single- electron on
2.2 Density functional theory (DFT)
HOHENBERG and KOHN [23] proved that the density distribution of electrons completely determines the properties of a system on the ground state and built the foundation of density functional theory (DFT), i.e. the KOHN-SHAM equation [24]:
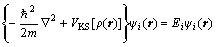 (2)
(2)
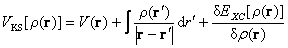 (3)
(3)
On the right side of Eqn.(3), the first item is the attracting potential between electrons and nuclei, the second item is the excluding potential between electrons, and the third is exchange and correlation potential. These equations indicate the complete establishment of DFT.
2.3 GGA method
The density distribution function and related properties of a system can be calculated according to the accurate expressions of energy density functional in KOHN-SHAM equation. But the completely accurate energy density functional cannot be known, so approximations have to be applied. And the common approximations of energy density functional are local density approximation (LDA) and GGA [21]. The basic idea of LDA is to get the exchange and correlation functional of inhomogeneous electron gas by the density function ρ(r) of homogeneous electron gas. In LDA, the density distribution of electrons can be calculated by solving a set of equations of single-electrons moving in the effective potential field. But in GGA, the exchange correlation potential is related to both the local density and the gradient of density function, and the calculated results can be improved in some cases.
2.4 Pseudopotential plane wave method
From the viewpoint of mathematics, any complete mathematic set can be taken as the initial solution of KOHN-SHAM equation, but the basis set of functions must be constructed elaborately to guarantee the convergence of the iteration solution process. Different basis functions have different advantages and disadvantages. And the common method based on DFT is pseudo-potential and plane wave method. There are other methods, such as full potential linear muffin-tin orbit (FPLMTO), and full potential linear augmented plane wave (FPLAPW) methods [25]. All these methods do not need any empirical parameters in calculations and have sound theoretical basis.
2.5 Calculation method
In this work, the GGA+PBE function and the ultrasoft pseudo-potential plane wave method were applied to calculate the lattice constants, total energies and densities of state of BCC-, FCC- and HCP-Fe, Ru, Os in ⅧB group [26]. The geometric optimization of lattice parameters was performed in original cell and the spin polarizing effect was considered. And to avoid the influence of Pulay stress [27], the total energy and other properties were calculated individually after a series of geometric optimizations with medium, fine and ultrafine qualities. At the same time, to accelerate the convergence of integration in Brilluin zone, the limited temperature Gaussian smearing was adopted [28].
3 Results
3.1 Calculation parameters
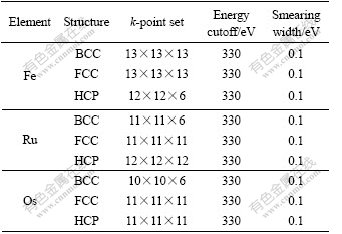
Table 1 lists the parameters after the geometric optimization and total energies calculated with ultrafine quality.
Table 1 Crystalline structures, k-point sets, cutoff energies and smearing widths of Fe, Ru and Os
3.2 Lattice constants and atomic volumes
Table 2 lists the results of lattice constants and atomic volumes of Fe, Ru and Os after geometric optimization.
Table 2 Lattice constants and atomic volumes of Fe, Ru and Os

3.3 Total energies and cohesive energies
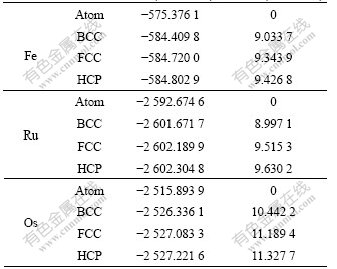
Table 3 lists the total energies and cohesive energies of Fe Ru and Os. Here, cohesive energy means the energy needed to separate the crystal at 0 K and 1.013×105 Pa into free atom in ground state [29]. And according to the definition of enthalpy H=U+pV, if the free atom state is chosen as the reference state, then item pV can be ignored due to the very small volume of condensed matter at 1.013×105 Pa. In this case, there exists H≈U for solid state matter. Then, the cohesive energy needed to separate solids into free atom in ground state can be approximately treated as U.
Table 3 Total energy and cohesive energy of Fe, Ru and Os
3.4 Density of state and atomic population
The difference of electronic structures is the intrinsic reason of lattice stability. The electronic structures of BCC-, FCC- and HCP-Fe, Ru, Os are calculated in this work. Figs.1-3 respectively show the total density of state (DOS), partial density of s state electrons, partial density of p state electrons, and partial density of d state electrons of BCC-, FCC- and HCP-Fe, Ru and Os, respectively. The atomic populations are presented in Table 4.
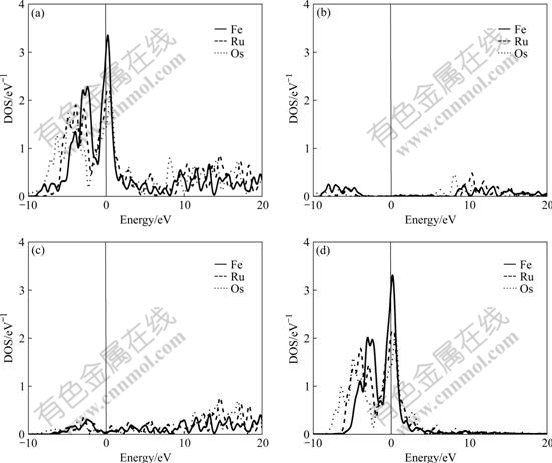
Fig.1 Total density (a), partial density of s state (b), partial density of p state (c), and partial density of d state(d) of BCC-Fe, Ru and Os
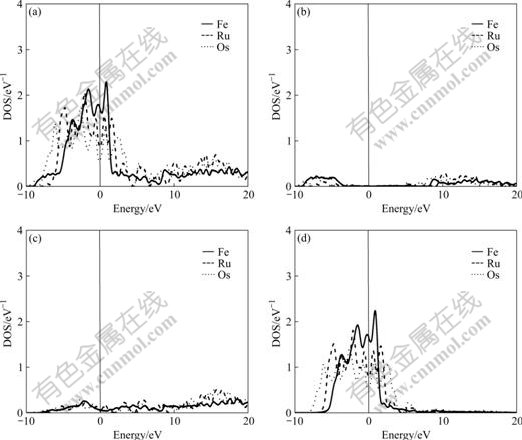
Fig.2 Total density (a), partial density of s state (b), partial density of p state (c), and partial density of d state (d) of FCC-Fe, Ru and Os
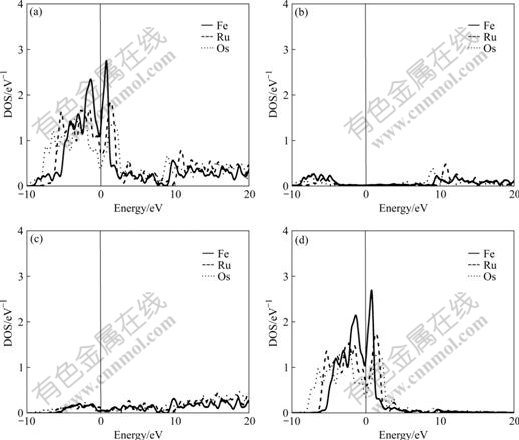
Fig.3 Total density (a), partial density of s state (b), partial density of p state (c), and partial density of d state (d) of HCP-Fe, Ru and Os
Table 4 Atomic population (AP) of BCC-, FCC-, HCP-Fe, Ru and Os
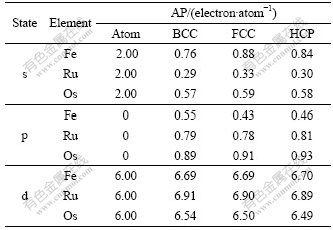
In Table 4, the electronic configurations of atomic Fe, Ru and Os in the ground state are respectively [Ar]3d64s2, [Kr]4d65s2 and [Xe] 4f145d66s2, and the total valence electron number is 8. When these atoms are condensed into crystals, the chemical bonds and energy bands form. Table 4 presents the changes of atomic population (AP) of BCC-, FCC-, HCP-Fe, Ru and Os.
4 Discussion
4.1 Lattice stability parameters
The lattice stability parameters are in fact the relative Gibbs energies, which describe the relative stability of phases. As for Fe, the lattice stability parameters are the energy differences (G-GBCC) of FCC and HCP phases relative to BCC phase. But for Ru and Os, the lattice stability parameters are the energy differences of BCC and FCC phases relative to HCP phase. For research convenience, the energy difference of (G-GHCP) was chosen for all the three elements. The function is dependent on temperature. But in this work, only the case at 0 K was discussed. So, there exists
?G =G-GHCP= H-HHCP≈U-UHCP (4)
And the results of total energy U calculated by the first-principles can be compared with those in SGTE database in CALPHAD method. The difference between CALPHAD method and the first-principles method and the difference between first-principles methods themselves can also be compared and discussed. The results are listed in Table 5.
Table 5 Lattice stability parameters of BCC-, FCC-, HCP-Fe, Ru and Os

It is shown in Table 5 that the lattice stability in CASTEP-GGA is ?GBCC-HCP>?GFCC-HCP>0 for all the three elements, which agrees with that of VASP-GGA and CALPHAD method except for BCC-Fe, and the relationship between lattice stability and electronic structure can be further discussed.
4.2 Lattice constants and atomic volumes
The comparison of lattice constants and atomic volumes obtained by first-principles method and experiment is shown in Table 6.
Table 6 Lattice constants and atomic volumes of BCC-, FCC-, HCP-Fe, Ru and Os

It is known from Table 6 that the lattice constants and atomic volumes calculated by CASTEP-GGA are smaller than those by VASP-GGA, and the atomic volumes of stable phases of HCP-Ru and HCP-Os are closer to the experimental data.
4.3 Total energy and cohesive energy
Cohesive energy is the total energy of condensed matter relative to free atom. In this paper, the free atom state was chosen as the reference state to calculate the differences of total energies between different structures in Table 7.
Table 7 Total energy of BCC-, FCC-, HCP-Fe, Ru and Os
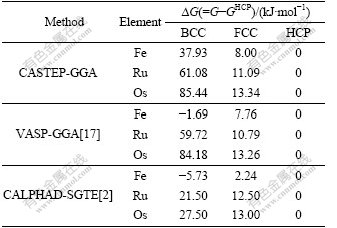
It is known that the total energies of the three elements by CASTEP-GGA are lower than those by VASP-GGA, and the results of both first-principles methods are different with those of experiments.
4.4 DOS and atomic populations
It is known from the comparison of total DOS, partial density of s state, partial density of p state and partial density of d state in Figs.1-3 that: (1) the electrons in s state are transferred into p and d states in the area from -10 to 0 eV, and all the electrons distribute widely, showing the strong hybridization between s, p and d states to construct crystals; (2) the Fermi energies of HCP-Ru and HCP-Os lie in the valley between two peaks of DOS with an obvious characteristic of stable phase, and those of FCC phases lie in the plat of peaks of DOS with the characteristic of unstable phase. These results agree well with the calculated results of the total energy.
The atomic population reflects the area below the curve of DOS, so the atomic populations in Table 4 can show the fine difference between the partial density of state(PDOS). It is known from Table 4 that: (1) most electrons in s state are transferred into p and d states to increase the bonding ability and strengthen the chemical bonding between atoms in crystals; (2) the transition number and rate vary with both the crystal structures and the elemental period. So the transition rate (δ) can be defined as
 (5)
(5)
where N1 is the number of electrons transferred from s to p or d state; and N2 is the total number of electrons transferred from s to p and d state.
The variation of δ with crystal structures and elemental period is listed in Table 8, and the transition electron number (TEN) is the number of the transferred electrons of s state.
Table 8 Transition electron number (TEN) of s state and transition rate (δ) of Fe, Ru and Os
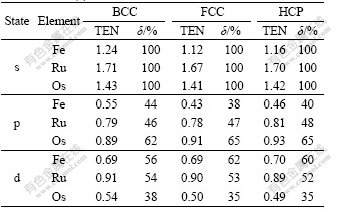
It is known from Table 8 that TENs from s to p state for BCC, FCC and HCP crystals of Fe, Ru and Os increase with the increase of elemental period, but those from s to d state decrease. For example, in the HCP crystals of Fe, Ru and Os, the transition rates of electrons from s to p state are respectively 40%, 48% and 65%, showing that with the increase of period, the electrons in s state are transferred into the stronger bonding p state dramatically with larger δ to form stronger cohesion, higher cohesive energy and more stable lattice in heavier metals.
5 Conclusions
(1) The calculations of lattice constants, total energies and densities of state of BCC- FCC-, HCP-Fe, Ru and Os in ⅧB group by total energy plane wave pseudopotential method of first-principles are performed. The results are compared with those of projector augmented wave method in first-principles, CALPHAD method and experimental data.
(2) The lattice stability of the three elements obtained by CASTEP-GGA method is ?GBCC-HCP>?GFCC-HCP>0 for Fe, Ru and Os, agreeing with that obtained by VASP-GGA and CALPHAD methods except for BCC-Fe.
(3) The lattice constants and atomic volumes of the three elements obtained by CASTEP-GGA are smaller than those by VASP-GGA, but the results of stable HCP-Ru and HCP-Os are closer to the experimental data, and the same case occurs in the total energy calculations.
(4) The electrons in s state are transferred into p and d states in the area from -10 to 0 eV, and all the electrons distribute widely, showing the strong hybridization between s, p and d states to construct crystals.
(5) The Fermi energies of HCP-Ru and HCP-Os lie in the valley between two peaks of DOS with an obvious characteristic of stable phases, agreeing well with the total energy calculations.
(6) The transition electron numbers from s to p increase dramatically in Fe, Ru and Os to form stronger cohesion, higher cohesive energy and more stable lattice in heavier metals.
References
[1] SAUNDERS N, MIODOWIK A P, DINDALE A T. Metastable lattice stabilities for the elements[J]. Calphad-Computer Coupling of Phase Diagrams and Thermochemistry, 1988, 12(4): 351-374.
[2] DINDALE A T. SGTE data for pure elements[J]. CALPHAD, 1991, 15(4): 317-425.
[3] JONES R O,GUNARSSON O. The density functional formalism, its applications and prospects [J]. Reviews of Modern Physics, 1989, 61(3): 689-746.
[4] KISSAVOS A E, SHALLCROSS S, KAUFMAN L, GR?N?S O, RUBAN A V, ABRIKOSOV I A. Thermodynamics of ordered and disordered phases in the binary Mo-Ru system[J]. Physical Review B, 2007, 75(18): 184203-184210.
[5] XIAO B, XING J D, FENG J, LI Y F, ZHOU C T, SU W, XIE X J, CHEN Y H. Theoretical study on the stability and mechanical property of Cr7C3[J]. Physica B, 2008, 403(13/16): 2273-2281.
[6] PENG J Z, WANG Y F, GRAY M F. First-principles study of structural stabilities and electronic properties of Mg-Nd intermetallic compounds[J]. Physica B, 2008, 403(13/16): 2344-2348.
[7] LV Z Q, SUN S H, JIANG P, WANG B Z, FU W T. First-principles study on the structural stability, electronic and magnetic properties of Fe2C[J]. Computational Materials Science, 2008, 42(4): 692-697.
[8] NAKAYAMA M, MATSUNO S, SHIRAKAWA J, WAKIHARA M. First-principles study on phase stability in LixCuSb with heusler-type structure[J]. Journal of Electrochemical Society, 2008, 155(7): 505-511.
[9] BRUTTI S, NGUYEN-MANH D, PETTIFOR D G. Lattice stability of Ca, Sr and Yb disilicides[J]. Intermetallics, 2006, 14(12): 1472-1486.
[10] GHOSH G, van de WALLE A, ASTA M. First-principles calculations of the structural and thermodynamic properties of bcc, fcc and hcp solid solutions in the Al-TM (TM=Ti, Zr and Hf) systems: A comparison of cluster expansion and supercell methods[J]. Acta Materialia, 2008, 56(13): 3202-3221.
[11] HILLYARD P B, GAFFNEY K J, LINDENBERG A M, ENGEMANN S, AKRE R A, ARTHUR J, BLOME C, BUCKSBAUM P H, CAVALIERI A L, DEB A, FALCONE R W, FRITZ D M, FUOSS P H, HAJDU J, KREJCIK P, LARSSON J, LEE S H, MEYER D A, NELSON A J, PAHL R, REIS D A, RUDATI J, SIDDONS D P. Carrier-density-dependent lattice stability in InSb[J]. Physical Review Letters, 2007, 98(12): 125501-125504.
[12] ASKER C, BELONOSHKO A B, MIKHAYLUSKIN A S, ABRIKOSOV A S. First-principles solution to the problem of Mo lattice stability[J]. Physical Review B, 2008, 77(22): 220102-220105.
[13] GRAD G B, BLAHA P, LUITZ J. Electronic structure and chemical bonding effects upon the bcc to Omega phase transition: Ab initio study of Y, Zr, Nb, and Mo[J]. Physical Review B, 2000, 62(19): 12743-12753.
[14] GUO G Y, WANG H H. Calculated elastic constants and electronic and magnetic properties of bcc, fcc, and hcp Cr crystals and thin films[J]. Physical Review B, 2000, 62(8): 5136-5143.
[15] SLUITER M H F. Ab initio lattice stabilities of some elemental complex structures[J]. Calphad-Computer Coupling of Phase Diagrams and Thermochemistry, 2006, 30(4): 357-366.
[16] SIN′KO G V, SMIRNOV N A. Ab initio calculations of elastic constants and thermodynamic properties of bcc, fcc, and hcp Al crystals under pressure[J]. Journal of Physics-Condensed Matter, 2002, 14(29): 6989-7005.
[17] WANG Y, CURTAROLO S, JIANG C. Ab initio lattice stability in comparison with CALPHAD lattice stability[J]. CALPHAD, 2004, 28(1): 79-90.
[18] GHOSH G, DELSANTE S, BORZONT G, ASTA M, FERRO R. Phase stability and cohesive properties of Ti-Zn intermetallics: First-principles calculations and experimental results[J]. Acta Materialia, 2006, 54(19): 4977-4997.
[19] GAO M C, ROLLETT A D, WIDOM M. Lattice stability of aluminum-rare earth binary systems: A first-principles approach[J]. Physical Review B, 2008, 75(17): 174120-174135.
[20] MILMAN V, WINKLER B, WHITE J A, PICKARD C J, PAYNE M C, AKHMATSKAYA E V, NOBES R H. Electronic structure, properties and phase stability of inorganic crystals: A pseudopotential plane-wave study[J]. International Journal of Quantum Chemistry, 2000, 77(5): 895-910.
[21] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple[J]. Physical Review Letters, 1996, 77(18): 3865-3868.
[22] LI Zhen-yu. Properties of novel materials from first principles[D]. Hefei: University of Science and Technology of China, 2004. (in Chinese)
[23] HOHENBERG P, KOHN W. Inhomogeneous electron gas[J]. Physical Review, 1964, 136(3B): 864-871.
[24] KOHN W, SHAM L J. Self-consistent equations including exchange and correlation effects[J]. Physical Review, 1965, 140(4A): 1133-1138.
[25] BLAHA P, SCHWARZ K, SORANTIN P, TRICKEY S B. Full-potential, linearized augmented plane wave programs for crystalline systems[J]. Computer Physics Communications, 1990, 59(2): 399-415.
[26] JOHN P P, WANG Y. Accurate and simple analytic representation of the electron-gas correlation energy[J]. Physical Review B, 1992, 45(23): 13244-13249.
[27] PULAY P. Convergence acceleration of iterative sequences: The case of scf iteration [J]. Chemical Physical Letters, 1980, 73(2): 393-398.
[28] METHFESSEL M, PAXTON A T. High-precision sampling for Brillouin-zone integration in metals[J]. Physical Review B, 1989, 40(6): 3616-3621.
[29] KITTEL C. Solid state physics[M]. New York: John Wiley and Sons Inc, 1976.
[30] MARK W. The University of Sheffield and Webelements Ltd [EB/OL]. 2006. http://www.weblements.com
Foundation item: Project(20070533118) supported by the Doctoral Discipline Foundation of Ministry of Education of China; Projects(50471058, 50271085) supported by the National Natural Science Foundation of China; Project supported by the Postdoctoral Foundation of Central South University, China
Received date: 2008-08-25; Accepted date: 2008-10-30
Corresponding author: TAO Hui-jin, PhD; Tel: +86-731-8830163; E-mail: thj@mail.csu.edu.cn
(Edited by CHEN Wei-ping)