横风作用下高速列车转向架非定常空气动力特性

郗艳红¹，毛军¹，高亮¹，杨国伟²

(1. 北京交通大学 土木建筑工程学院，北京，100044；

2. 中国科学院力学研究所，北京，100190)

摘要：针对CRH型动车组的真实外形，采用分离涡数值计算方法，对横风中高速列车转向架的非定常空气动力特性进行研究。得到各个转向架气动荷载的时域特性、频域特性以及转向架周围非定常流动结构。研究结果表明，横风中高速列车转向架处流场非常紊乱，伴生出许多分离涡；转向架所受的空气动力存在非常明显的非定常性；各个转向架空气动力的功率谱密度存在明显峰值，若转向架或转向架中某些弹性体的固有频率与它们耦合，则易出现共振进而失稳的情况。本研究可以为高速列车局部减阻优化设计和提高高速列车自身的抗风性能设计提供 参考。

关键词：转向架；横风；功率谱密度；非定常空气动力；高速列车

中图分类号：U271.91           文献标志码：A         文章编号：1672-7207(2014)05-1705-10

Aerodynamic force/moment for high-speed train bogie in crosswind field

XI Yanhong¹, MAO Jun¹, GAO Liang¹, YANG Guowei²

(1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;

2. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China)

Abstract: For the real configuration of CRH with bogies and pantograph running in crosswind, the unsteady aerodynamic characteristics of bogies were studied numerically by the 3D detached-eddy simulation method. The characteristics of the unsteady forces acting on the bogies were presented from the numerical results, which included the characteristics of the time domain and the frequency domain, and the flow structures. The numerical results indicate that the aerodynamic forces on the bogies have strong unsteady characteristics. The unsteady aerodynamic forces have obvious peaks in their frequency domain. If the modal frequency range of bogies interconnected with this frequency, the bogies as a dynamical system will be resonated by the unsteady aerodynamic forces due to the crosswind and the resonance can lead to reducing of the operating safety of the train, and even lead to overturning of the train. The results are helpful to local drag-reduced optimization and train wind resistance design.

Key words: bogie; crosswind; power spectrum density; unsteady aerodynamic force/moment; high-speed train

转向架是轨道车辆结构中最为重要的部件之一，起支承车体并传递从车体至车轮之间或从轮轨至车体之间的各种载荷及作用力。随着列车运行速度的越来越高，再加上风荷载的作用，转向架不仅是轮轨关系及地面效应研究的基础，还影响到列车的气动性能及运行安全性。但是目前对侧风效应所引起的安全性问题分析较多^[1-5]，对于转向架气动特性的研究却很少^[6-8]。另外，组成转向架的各部件在列车运动过程中均处于振动状态，对于其模态振型和模态频率的分析是转向架设计时的重要内容，但对此的研究较少。本文作者以某CRH型高速列车在平原上运行为例，根据其真实外形和细部结构建模，分析其转向架绕流的非定常瞬态特性，为车辆设计及提高列车自身的抗风性能与运行安全性提供参考。转向架尾涡的流场非常复杂，包含各种不同尺度的漩涡，要准确模拟转向架尾部的流场，就必须准确捕捉转向架尾部各种尺度的涡结构。分离涡模拟(DES)基本思想是：在近壁面附近采用雷诺时均(RANS)方法，用湍流模型模拟其中的小尺度脉动运动；在远离物面的区域，采用大涡模拟(LES)方法模拟脱体涡运动。这样既可在附面层内发挥RANS方法计算量小的优势，又可在远离物面的区域对大尺度的脱体分离涡进行较好模拟。由于分离涡模拟兼有雷诺时均方法和大涡模拟的优点，逐渐受到科研人员的重视，并应用到像列车这种长大物体周围的瞬态流场的模拟，计算结果和实验结果基本吻合^[9-14]，因此，本文作者采用分离涡模拟法(DES)进行数值模拟计算。

1  计算模型及条件

由于列车中部截面不变，缩短的模型不改变列车流场结构的基本特征^[15]，因此采用3辆车编组，即头车+中间车+尾车，长度分别为25.675，24.775和25.675 m，列车宽度为3.265 m，高度为3.89 m，考虑转向架、受电弓、风挡、空调导流罩等细部结构，头车和尾车均为流线型。主要的计算条件和方法如下：

(1) 列车车速300 km/h；横风风速20 m/s，采用指数风，即在气象上10 m高度处的风速为20 m/s，横风风向角为90°，指数风场按照文献[16]确定；

(2) 采用trim网格，加密列车周围、列车尾流、列车背风侧等流场变化大的区域。在近壁面区采用壁面函数法，列车壁面和地面的边界层均设15层，近壁面第1层网格到壁面的距离均为0.2 mm，网格总量约为8 200万；

(3) 采用分离涡方法进行非定常计算，基于Menter k-ω SST两方程湍流模型，经反复试算，考虑计算精度及效率2方面因素，确定非定常计算的时间步长为5×10^-4 s，每一个时间步内进行20次子迭代，通过监测列车气动力参数以保证每一个时间步内的计算收敛，总共计算4 000个时间步，并保存每一时间步的有效数据，非定常时程为2 s。计算时首先使用雷诺时均法对定常流场进行求解，得到的结果作为非定常流场的初始解，即初始条件。然后再使用分离涡模拟方法进行非定常流场计算。数值模拟计算采用的模型及计算域如图1所示。

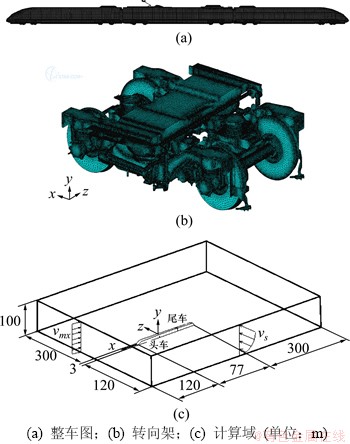
图1  所用模型及计算域

Fig. 1  Geometric model and computational domain

2  结果分析

2.1  转向架气动荷载的时域特性

转向架的气动阻力、升力和横向力分别由转向架表面分布的压力和切应力在列车运动方向、铅垂方向及水平方向上的投影积分得到，结果如图2~4所示。

2.1.1  气动阻力的时域特性

由图2可知：转向架的气动阻力都围绕某一时均值上下脉动。同一车辆上的前、后转向架的气动阻力的瞬态值和平均值不同，脉动周期也不尽相同。对于头车和尾车，前转向架的阻力比后转向架的大，而对于中间车的则相反。前、后转向架的阻力平均值相差最高可达800 N，占较大平均值的1/3，瞬态阻力差值更大。尾车前、后转向架的时变周期曲线的反相变化规律比较明显，即在前转向架的阻力增大时，后转向架的阻力却同时减少。头车和中间车的阻力时变周期曲线的反相性质则不明显。

由图3可知：转向架的气动升力都围绕某一时均值上下脉动。同一车辆上的前、后转向架的气动升力的瞬态值和平均值不同，脉动周期也不尽相同。对于头车，前转向架在全时程内受到的都是负升力，后转向架的升力则在0附近脉动、周期性地正负交替，均值接近于0；中间车的前转向架在全时程内受到的都是负升力，均值为负，而后转向架受到的则都是正升力，均值为正。中间车的前、后转向架的升力平均值相差最高可达800 N，占较大平均升力绝对值的2/3。尾车前转向架的升力在较小的负值附近周期性地正负交替，后转向架则始终受到负升力的作用。尾车的前、后转向架的时变周期曲线的反相变化规律比较明显，即在前转向架的升力增大时，后转向架的升力却同时减少。

2.1.2  气动横向力的时域特性

由图4可知：各转向架的气动横向力都围绕某一时均值上下脉动。同一车辆上的前、后转向架的气动横向力的瞬态值和平均值不同，脉动周期也不尽相同。全部转向架的横向力在全时程内均为正值，即与横风方向一致。对于头车，前转向架的横向力较大，比后转向架的大0.1 kN左右，但后转向架的横向力波动较大，波幅接近0.8 kN，约为平均值(1.4 kN)的60%。对于中间车，后转向架横向力的平均值比前转向架的大0.5 kN左右，且波动幅值较大，最大波幅可达1.2 kN，与平均值相当。尾车前转向架的横向力及横向力的波动幅值均大于后转向架的。中间车的前、后转向架的横向力变化具有一定的反相变化规律，即在前转向架的横向力增大时，后转向架的横向力却同时减少。头车的横向力在部分时程内表现出反相变化规律。

2.1.3  倾覆力矩的时域特性

不同转向架的倾覆力矩时变曲线如图5所示。由图5可知：各转向架的倾覆力矩都围绕某一时均值上下脉动。同一车辆上的前、后转向架的倾覆力矩的瞬态值和平均值不同，脉动周期也不尽相同。对于头车，转向架的倾覆力矩在全时程内基本为正值，后转向架的倾覆力矩时均值较大，比前转向架的大0.6 kN×m左右；但前转向架的横向力波动较大，最大波幅接近0.85 kN×m，约为平均值(0.56 kN×m)的150%。对于中间车，后转向架的倾覆力矩在全时程内均为正值，最大波幅约为0.9 kN×m，约为平均值(1.2 kN×m)的75%；前转向架的倾覆力矩基本为负值，其平均值约为-0.3 kN×m，且波动幅值较大，最大波幅可达1.5 kN×m。对于尾车，前转向架的倾覆力矩一直保持为正值，后转向架的则在时均值-0.3 kN×m附近大幅度波动。中间车的前、后转向架的倾覆力矩变化具有一定的反相性质，即在前转向架的倾覆力矩增大时，后转向架的却同时减少。头车和尾车的在部分时程内表现出反相性质。

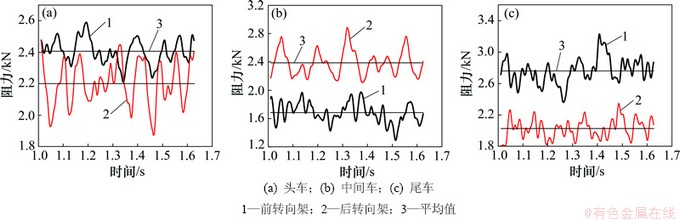
图2  不同转向架的阻力时变曲线

Fig. 2  Drag curves changing with time on different bogies

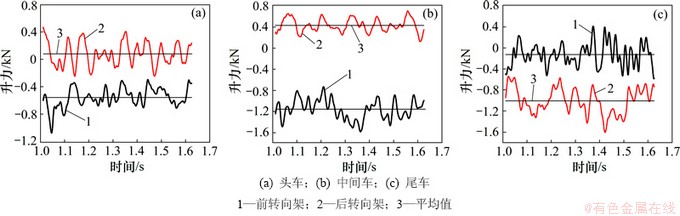
图3  不同转向架的升力时变曲线

Fig. 3  Lift force curves changing with time on different bogies

2.1.4  侧偏力矩和俯仰力矩的时域特性

不同转向架的侧偏力矩时变曲线如图6所示。由图6可知：头车和中间车的前转向架的侧偏力矩均为正值，后转向架的则全部为负值，而且两者各自的前、后转向架的侧偏力矩的时均值都相差很大。尾车的前转向架的侧偏力矩均为负值，后转向架的为正值。各个转向架的侧偏力矩的波动幅度都比较大。

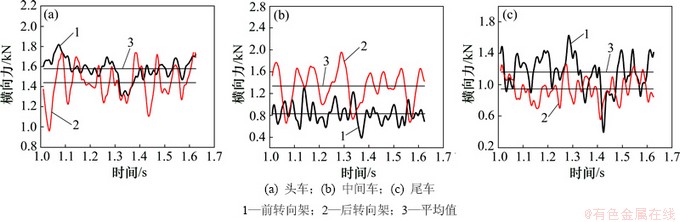
图4不同转向架的横向力时变曲线

Fig. 4  Lateral force curves changing with time on different bogies

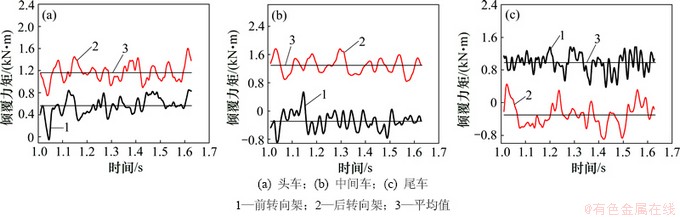
图5  不同转向架的倾覆力矩时变曲线

Fig. 5  Overturning moment curves changing with time on different bogies

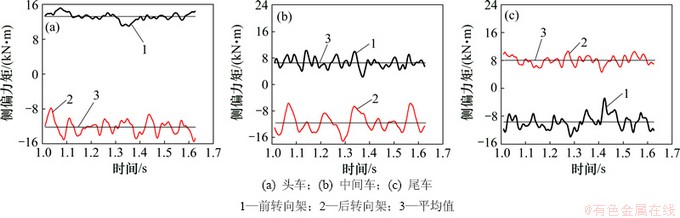
图6  不同转向架的侧偏力矩时变曲线

Fig. 6  Lateral moment curves changing with time on different bogies

不同转向架的俯仰力矩时变曲线如图7所示。由图7可知：头车和中间车的前、后转向架的俯仰力矩均为正值，而且后转向架的相对波幅较大。尾车的后转向架的俯仰力矩均为正值，后转向架的则在部分时刻出现负值。

需要指出的是，各转向架的各种气动荷载不相同。由文献[17]可知：高速列车在横风中运行时，头车、中间车和尾车的绕流流场十分复杂。尤其在转向架区域，转向架几何外形复杂，转向架、车体底部的离地间隙相差较大，因此，流经不同转向架的流场差别也较大，从而使各转向架受到的各种气动荷载具有不同的变化规律。

2.2  转向架气动荷载的频域特性

2.2.1  气动阻力的频域特性

为了分析各工况下高速列车所受空气动力的周期性，对各工况下各车辆的空气动力时域信号进行功率谱密度计算。

不同转向架的阻力功率谱密度特性如图8所示。由图8可知：全车阻力功率谱密度峰值的频率集中在20 Hz以内，同一车辆的前后转向架的功率谱密度峰值相差2~3倍；头车和中间车的后转向架的阻力功率谱密度远比前转向架的高，对应的峰值频率为12.987和8.117 Hz；尾车的则是前转向架的阻力功率谱密度远比后转向架的高，前、后转向架的峰值频率均为9.740 Hz，而且前转向架有比较接近的2个功率谱密度峰值，即主频为9.740 Hz，次频为3.999 Hz。

2.2.2  气动升力的频域特性

不同转向架的升力功率谱密度特性如图9所示。由图9可知：升力功率谱密度峰值的频率集中在50 Hz以内，同一车辆的前后转向架的功率谱密度峰值相差1~3倍。头车的前、后2个转向架均有多个峰值频率，后转向架的主频为17.857 Hz，次频为12.987 Hz，功率谱密度为3.5×10³ N²×Hz^-1左右；前转向架的主频为6.494 Hz，次频为1.664 Hz，功率谱密度为1.5×10³~2.0×10³ N²×Hz^-1。中间车的前、后转向架的功率谱密度峰值非常接近，大约为3.75×10³ N²×Hz^-1，对应的主频分别为1.623 Hz和8.117 Hz，前转向架的次频为9.740 Hz；尾车的后转向架的升力功率谱密度远比前转向架的高，前者接近13.0×10³ N²×Hz^-1，对应的峰值频率为3.247 Hz，后者仅为3.5×10³ N²×Hz^-1左右。

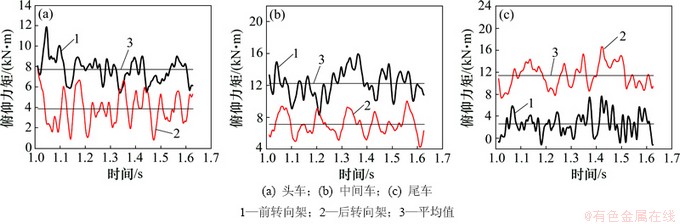
图7  不同转向架的俯仰力矩时变曲线

Fig. 7  Pitching moment curves changing with time on different bogies

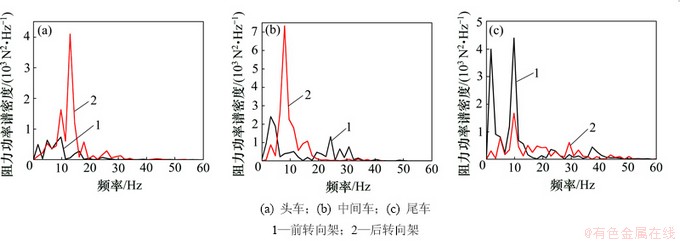
图8  不同转向架的阻力功率谱密度特性

Fig. 8  Pitching moment curves changing with time on different bogies

2.2.3  气动横向力频域特性

不同转向架的横向力时变曲线和功率谱密度特性如图10所示。由图10可知：横向力功率谱密度峰值的频率集中在30 Hz以内，同一车辆的前后转向架的功率谱密度峰值可相差1~7倍。对于头车，其前、后转向架均有多个峰值频率，后转向架的主频为12.990 Hz，功率谱密度最大峰值为7.538 5×10³ N²×Hz^-1，次频为9.740 Hz；前转向架的主频为1.623 Hz，功率谱密度峰值为3.059×10³ N²×Hz^-1，次频为4.870 Hz。中间车的前、后转向架的功率谱密度最大峰值相差很大，分别为3.023×10³和18.423×10³ N²×Hz^-1，对应的主频分别是8.117 Hz和24.350 Hz。而对于尾车，其前、后转向架有多个功率谱密度峰值，且前者远高于后者的，前转向架的次频所对应的功率谱密度峰值也高于后转向架的；前、后转向架的主频分别是9.740 Hz和3.250 Hz，对应的功率谱密度峰值分别是7.064 3×10³和2.649 4×10³ N²×Hz^-1。

2.2.4  倾覆力矩的频域特性

不同转向架的倾覆力矩功率谱密度特性如图11所示。由图11可知：倾覆力矩功率谱密度峰值的频率集中在50 Hz以内，同一车辆的前后转向架的功率谱密度峰值可相差1~4倍。头车和中间车的前、后转向架各自均有多个峰值频率。对于头车，其前转向架的主频为8.120 Hz，功率谱密度峰值为3.40×10³ N²×m²×Hz^-1，次频为14.610 Hz，后转向架的主频为12.990 Hz，功率谱密度最大峰值为5.031×10³ N²×m²×Hz^-1，次频为4.870 Hz；对于中间车，前、后转向架的功率谱密度最大峰值分别为5.284 7×10³和7.887 4×10³ N²×m²×Hz^-1，对应的主频分别为6.490 Hz和8.120 Hz。而对于尾车，后转向架的功率谱密度峰值远比前转向架的高；前、后转向架的主频分别为9.740 Hz和3.240 Hz。

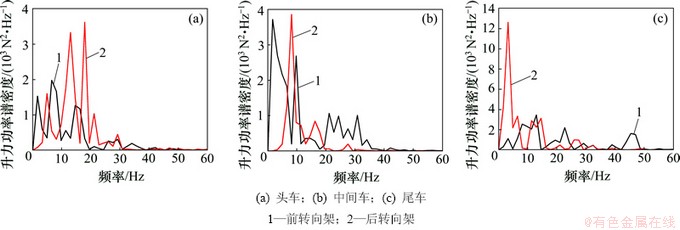
图9  不同转向架的升力功率谱密度特性

Fig. 9  Power spectral density of lift force for different bogies

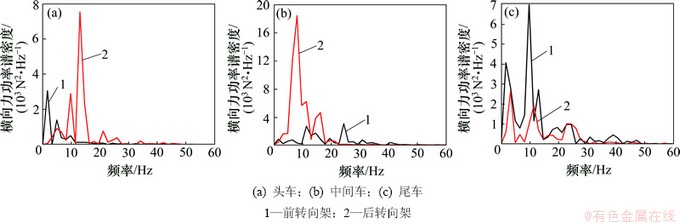
图10  不同转向架的横向力功率谱密度特性

Fig. 10  Power spectral density of lateral force for different bogies

2.2.5  侧偏力矩和俯仰力矩频域特性

不同转向架的侧偏力矩功率谱密度曲线和俯仰力矩功率谱密度特性如图12和13所示。由图12和13可知：3节车辆均是后转向架的功率谱密度峰值远高于前转向架的，但对应的主频却各不相同。

荷载峰值波幅较大，若峰值荷载较大且持续时间较长，也就是说频率较低、能量集中，则会对转向架的稳定运行产生影响。表1所示为各节车辆上各个转向架的气动荷载功率谱密度峰值及对应的频率。从表1可以看出：这些最大功率谱密度峰值对应的频率主要集中在1.664~12.990 Hz，在此频率下，气动荷载的能量集中作用于转向架，若转向架或转向架中某些弹性体的固有频率与它们耦合，则易出现共振进而失稳的情况。因此，最好采取措施使转向架的模态频率避开这些频率段。

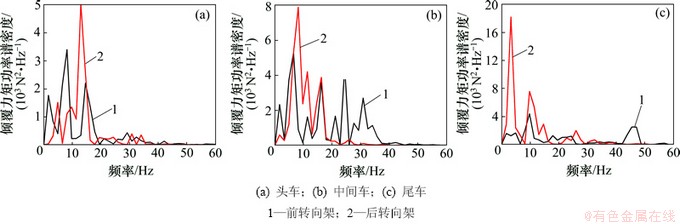
图11  不同转向架的倾覆力矩功率谱密度特性

Fig. 11  Power spectral density of overturning moment for different bogies

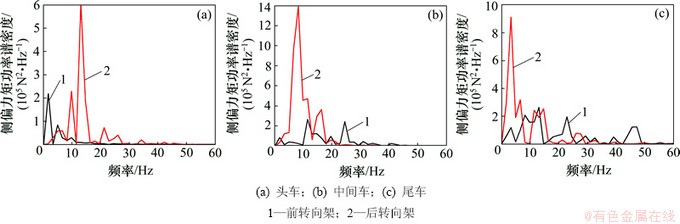
图12  不同转向架的侧偏力矩功率谱密度曲线

Fig. 12  Power spectral density of lateral moment for different bogies

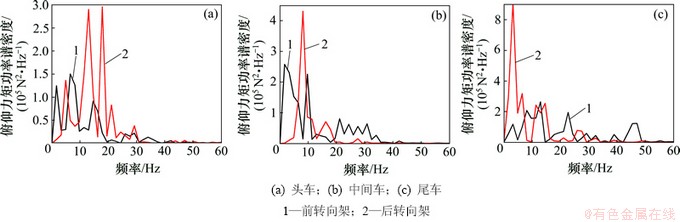
图13  不同转向架的俯仰力矩功率谱密度特性

Fig. 13  Power spectral density of pitching moment for different bogies

2.3  转向架非定常流场

由于转向架所受空气动力由转向架周围流场产生，因此转向架所受空气动力的非定常特性也必定是由转向架周围的非定常流动所致。为了进一步分析转向架所受非定常空气动力产生的原因，对转向架周围流场进行研究。

在列车上取若干截面(如图14所示)，以切过转向架的S11和未切过转向架的S12截面为例，对其流场结构进行分析。列车上横截面S11和S12非定常流动的流线图如图15和16所示。由图15可知：在不同的时刻，转向架所在截面的车体底部存在较多不稳定的小分离涡。

随着时间的推进，列车背风侧分离涡的几何尺度和位置均发生变化，分离涡的数量也发生改变。在整个过程中始终存在着主流分离涡A，但其形状、尺寸和位置发生变化，并伴生出附加的小尺度分离涡。在t=0.1 s时，背风侧壁面上下转角处开始形成小分离涡B和C；小涡C在t=0.5 s时形成，在t=1.0 s时破碎扩散，在t=1.2 s时又重新开始构造，至t=1.4 s时完全形成；而小涡B在t=1.0 s时初现雏形，在t=1.4 s时完全形成，在t=2.0 s时又破碎扩散。其间，在t=1.4 s时，生成了小涡D，一共有4个分离涡出现，该时刻是背风侧出现分离涡相对最多的时刻，随后又恢复到3个。可见，列车周围的流场和转向架处的紊流流场相互影响，进而影响到车体侧面下方的流场，伴生出一些分离涡，而在无转向架的截面(如图16所示)，车体底部未见有明显的分离涡。这一现象说明，转向架的扰动对非定常流动的影响较大，也是引起局部非定常流动的因素，进而转向架处产生了非定常的空气动力特性。

表1  转向架气动荷载的功率谱密度的频率

                          Table 1  Frequency of power spectral density for bogies                       Hz

图14  列车纵向的横截面位置

Fig. 14  Cross section position along train

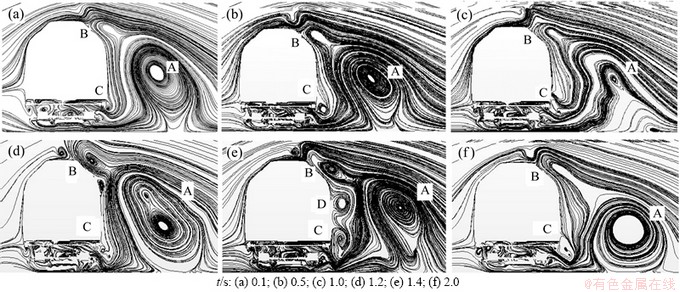
图15  列车上横截面S11非定常流动的流线图

Fig. 15  Unsteady streamline with cross section of S11

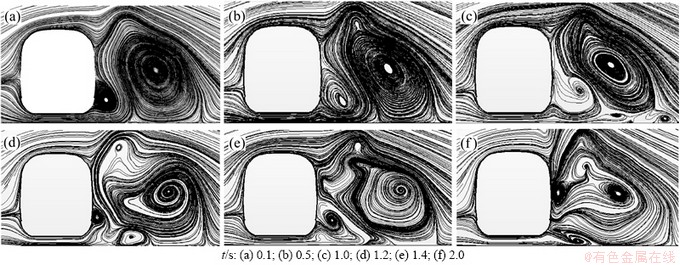
图16  列车上横截面S12非定常流动的流线图

Fig. 16  Unsteady streamline with cross section of S12

3  结论

(1) 横风中高速列车转向架所受空气动力存在明显的非定常性，各个转向架的气动力都围绕某一时均值上下脉动。不同车辆的转向架、同一车辆上的前后转向架的气动荷载的时均值、脉动量和脉动周期等均不相同，同一转向架的6个气动荷载分量的脉动参数也不相同。

(2) 通过对高速列车转向架所受非定常空气动力的频域分析可以发现,各个转向架的空气动力在功率谱密度图中存在明显峰值，这些最大功率谱密度峰值对应的频率主要集中在1.664~12.990 Hz。若转向架或转向架中某些弹性体的固有频率与它们耦合，则易出现共振进而失稳的情况。

(3) 通过对高速列车转向架周围非定常流场分析可知，在横风影响下, 转向架处流场非常紊乱，伴生出一些分离涡，从而影响到车体侧面下方的流场，是引起局部非定常流动的原因；而在无转向架的截面，车体底部未见有明显的分离涡。

参考文献：

[1] Suzuki M, Tanemoto K, Maeda T. Aerodynamic characteristics of train/vehicles under cross wind[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(1): 209-218.

[2] Stephane S, Christian B, Marc D, et al. Effect of cross winds on high-speed trains: Development of a new experimental methodology[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2004, 92(7/8): 535-545.

[3] Carrarini A. Reliability based analysis of the crosswind stability of railway vehicles[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(7): 493-509.

[4] 周丹, 田红旗, 杨明智, 等. 强横风下客车在不同路况运行的气动性能比较[J]. 中南大学学报(自然科学版), 2008, 39(3): 554-559.

ZHOU Dan, TIAN Hongqi, YANG Mingzhi, et al. Comparison of aerodynamic performance of passenger train traveling on different railway conditions up strong cross-wind[J]. Journal of Central South University (Science and Technology), 2008, 39(3): 554-559.

[5] 高广军, 苗秀娟. 强横风下青藏线客车在不同高度桥梁上的气动性能分析[J]. 中南大学学报(自然科学版), 2010, 41(1): 376-380.

GAO Guangjun, MIAO Xiujuan. Aerodynamic performance of passenger train on different height of bridge of Qinghai-Tibet railway line under strong cross wind[J]. Journal of Central South University (Science and Technology), 2010, 41(1): 376-380.

[6] 黄学辉. 转向架对高速列车气动特性影响研究[D]. 成都: 西南交通大学机械工程学院, 2008: 10-40.

HUANG Xuehui. Influence of bogie on aerodynamic characteristic of high-speed trains[D]. Chengdu: Southwest Jiaotong University. School of Mechanical Engineering, 2008: 10-40.

[7] 郗艳红, 毛军, 李明高, 等. 高速列车侧风效应的数值模拟[J]. 北京交通大学学报, 2010, 34(1): 14-19.

XI Yanhong, MAO Jun, LI Minggao, et al. Numerical study on the crosswind effects of high-speed train[J]. Journal of Beijing Jiaotong University, 2010, 34(1): 14-19.

[8] 郑循皓, 张继业, 张卫华. 高速列车转向架空气阻力的数值模拟[J]. 交通运输工程学报, 2011, 11(2): 45-51.

ZHENG Xunhao, ZHANG Jiye, ZHANG Weihua. Numerical simulation of aerodynamic drag for high-speed train bogie[J]. Journal of Traffic and Transportation Engineering, 2011, 11(2): 45-51.

[9] Ghuge H. Detached eddy simulations of a simplified tractor/trailer geometry[D]. Alabama: Auburn University. Department of Aerospace Engineering Auburn, 2007: 1-101.

[10] Villiers E, Jackson A, Campos F. Aerodynamic simulations using vertically integrated open source solutions[C]// Proceedings of 7th MIRA International Vehicle Aerodynamics Conference. Coventry, UK: Mira Ltd, 2008: 378-388.

[11] Diedrichs B. Aerodynamic crosswind stability of a regional train model[J]. Proceedings of the Institution of Mechanical Engineers (Part F): Journal of Rail and Rapid Transit, 2010, 224(6): 580-591.

[12] Emmanuel G. Numerical simulation with a DES approach[J]. SAE International Journal of Passenger Cars: Mechanical Systems, 2010, 3(1): 574-587.

[13] Tristan F, Gunilla E. An assessment of detached-eddy simulations of unsteady crosswind aerodynamics of road vehicles[J]. Flow, Turbulence and Combustion, 2011, 87(1): 132-163.

[14] 苗秀娟, 高广军. 基于DES的车辆横风气动性能模拟[J]. 中南大学学报(自然科学报), 2012, 43(7): 2855-2860.

MIAO Xiujuan, GAO Guangjun. Aerodynamic performance of train under cross-wind based on DES[J]. Journal of Central South University (Science and Technology), 2012, 43(7): 2855-2860.

[15] Khier W, Breuer M, Durst F. Flow structure around trains under side wind conditions: A numerical study[J]. Computers and Fluids, 2000, 29(2): 179-195.

[16] 毛军, 郗艳红, 杨国伟. 侧风风场特征对高速列车气动性能作用的研究[J]. 铁道学报, 2011, 33(4): 22-30.

MAO Jun, XI Yanhong, YANG Guowei. Research on influence of characteristics of cross wind field on aerodynamic performance of a high-speed train[J]. Journal of the China Railway Society, 2011, 33(4): 22-30.

[17] 郗艳红. 横风作用下的高速列车气动特性及运行安全性研究[D]. 北京: 北京交通大学土木建筑工程学院, 2013: 12-20.

XI Yanhong. Research on aerodynamic characteristics and running safety of high-speed trains under cross winds[D]. Beijing: Beijing Jiaotong University. School of Civil Engineering, 2013: 12-20.

(编辑  赵俊)

收稿日期：2013-05-08；修回日期：2013-08-25

基金项目：国家自然科学基金资助项目(51278032)；“十一五”国家科技支撑计划重大项目(GTYZ200902)；中国博士后科学基金资助项目(2013M530520)

通信作者：毛军(1966-)，男，湖北公安人，教授，博士生导师，从事空气动力学及火灾安全研究；电话：13331103265；E-mail: jmao@bjtu.edu.cn