文章编号：1004-0609(2014)05-1333-06

Ru掺杂Sn基氧化物电极的第一性原理计算

刘雪华^{1, 2, 3}，邓芬勇^{1, 2}，翁卫祥^{1, 2}，王  欣^{1, 2}，林  玮¹，唐  电^{1, 2}

(1. 福州大学 材料研究所，福州 350108；

2. 福州大学 材料科学与工程学院，福州 350108；

3. 福建工程学院 材料科学与工程学院，福州 350108)

摘  要：采用基于密度泛函理论的平面波超软赝势方法和局域密度近似，研究Ru掺杂SnO₂形成的Sn_0.875Ru_0.125O₂复合氧化物电极的晶体结构和电子结构，比较掺杂前后体系的能带结构、电子态密度和载流子浓度。计算表明： Ru掺杂后SnO₂的晶胞体积缩小，复合氧化物电极的能带结构、电子态密度和载流子浓度均发生显著变化，导致材料的导电类型呈现近金属特性，揭示Ru掺杂后SnO₂导电性能显著增强的原因是导带底附近形成的杂质能级的贡献。

关键词：Sn基氧化物；Ru掺杂；第一性原理计算；电子结构；导电性能

中图分类号：TG174.4　　     文献标志码：A

First-principles calculation of Ru-doping Sn-based oxide electrode

LIU Xue-hua^{1, 2, 3}, DENG Fen-yong^{1, 2}, WENG Wei-xiang^{1, 2}, WANG Xin^{1, 2}, LIN Wei², TANG Dian^{1, 2}

(1. Institute for Materials Research, Fuzhou University, Fuzhou 350108, China;

2. College of Material Science and Engineering, Fuzhou University, Fuzhou 350108, China;

3. College of Materials Science and Engineering, Fujian University of technology, Fuzhou 350108, China)

Abstract: The lattice structure and the electronic properties of the composite oxide electrode, Sn_0.875Ru_0.125O₂, formed by doping Ru into SnO₂ were investigated with the ultra soft pseudo potential plane wave method and the local density approximation within density functional theory. The band structure, density of states and concentration of carrier of the Sn-based oxides before and after doping were compared. The results show that the cell volume of the system decreases and the band structure, density of states and concentration of carrier of the SnO₂ all change significantly after Ru doping. All these changes lead to the similar metallic conductive mechanism of the Sn_0.875Ru_0.125O₂. And then the physical essence of electronic structure changes leading to significant enhances of the conductive performance of the SnO₂ doping Ru was revealed.

Key words: Sn-based oxides; Ru-doping; first-principles calculation; electronic structure; conductive performance

RuO₂具有优越的导电性，可以被用作析氯^[1-2]、析氧^[3]、超电容^[4]和燃料电池^[5]的电极材料。但是Ru资源有限且价格昂贵，因而限制了其应用。人们发现具有金红石结构的氧化物TiO₂和SnO₂可以与RuO₂形成固溶体^[6]，这类第二组元的引入可以明显增强RuO₂与贵金属氧化物的之间的协同作用。大量研究发现，如果在SnO₂基体中添加Ru可获得固溶体电极材料，该方法不仅可以降低成本，而且可以提高其性能。普遍应用的Ru-Sn氧化物电极材料的主要结构都是含Ru的Sn基氧化物固溶体。有研究表明^[7]，只要添加1.4%(质量分数)的Ru即可得到性能优良的电极材料。但Ru掺杂后SnO₂的导电性发生明显改善的机理尚未见深入研究的报道，而对于与导电性直接相关的电极材料而言，电子结构的研究是解释这一现象的重要方面。因此，本文作者引入密度泛函理论的第一性原理方法，以SnO₂和经Ru置换Sn形成的Sn_0.875Ru_0.125O₂固溶体为研究体系，对其晶体结构和电子结构进行计算，对比研究添加Ru前后SnO₂电极的能带结构、态密度和载流子浓度，在此基础上分析掺杂Ru对SnO₂电极材料导电性能的影响，找出含Ru电极材料具备优良导电性能的物理依据，为其广泛应用提供理论上的支持。

1  研究方法

考虑到常规SnO₂基氧化物电极材料以金红石为骨架结构，添加的Ru与SnO₂形成Sn_1-xRu_xO₂置换固溶体^[8]，故在此考虑以金红石结构为原型，其空间群为P42/mnm。对于Sn_0.875Ru_0.125O₂固溶体，可通过在构建的SnO₂的2×2×1超胞中以一个Ru原子将一个Sn原子替换来建立模型，超胞结构如图1所示，其中Ru原子的位置是无序分布的。计算工作由VASP程 序软件包完成，交换关联势采用局域密度近似LDA，波函数通过平面波来展开；经过不同条件的测试，本研究中采用6×6×6 Monkhorst-Pack特殊点对布里渊区进行分割，平面波截断能取520 eV^[9-10]。详细的计算方法参见文献[11-12]。为保证计算的精度要求，本研究中自洽场的收敛标准为原子总能变化低于2×10^-5 eV/atom，原子受力小于0.5 eV/nm，位移公差小于2.0×10^-4 nm，最大张力不超过0.1 GPa。能量计算都在倒易空间中进行，采用周期性边界条件。由于RuO₂-SnO₂平衡体系的端际氧化物固溶度很低^[12]，Sn_0.875Ru_0.125O₂固溶体不能稳定存在，但采用常规工艺可以在30%~70%(摩尔分数)间得到亚稳定的固溶体电极材料^{[2, 8, 13]}。故在本计算中，本文作者构筑了不同组态的Sn_0.875Ru_0.125O₂置换固溶体，通过几何结构优化，得到能量最低的一种固溶体组态，并假设它属于常见电极材料的结构。再利用Murnaghan状态方程式来确定平衡状态的SnO₂和Sn_0.875Ru_0.125O₂的总能和体积，从而获得折合的晶胞参数a和c，之后进一步计算体系的电子结构。

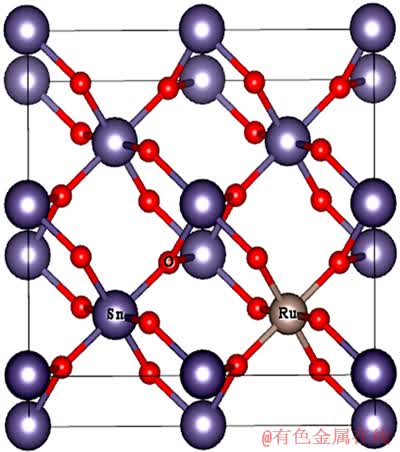
图1  Sn₇Ru₁O₁₆超胞的结构示意图

Fig. 1  Supercell structure of Sn₇Ru₁O₁₆

2  结果与讨论

2.1  晶体结构

图2所示为通过计算获得的掺杂前后超胞的总能与超胞体积的对应关系。由图2可知，所有计算数值均随体积增大呈现类似抛物线的变化特征，即体系总能随体积增大发生由高至低、达某一最低点后再回升的变化趋势，而此最低点则为体系总能稳定存在的状态。对这些计算数据点，采用Murnaghan 状态方程进行拟合后发现，拟合曲线与计算数据点十分吻合，说明本计算中的条件设定较为合理。表1列出经计算获得的折合的点阵常数和文献报道中的SnO₂和RuO₂相应数据。需指出的是，文献中尚未找到采用ab-initio原理计算Sn_0.875Ru_0.125O的数据。在此，将计算得到的RuO₂和SnO₂的晶格参数和文献报道的数据^{[9-10, 14]}进行了比较，结果见表1。本计算中得到的两个端际氧化物的晶格参数结果与报道的理论或实验数据均很接近，与其他文献的数据相比，相对误差(ΔV/V_card)很小(见表1)，表明采用ab-initio的计算方法和计算结果是可以接受的。

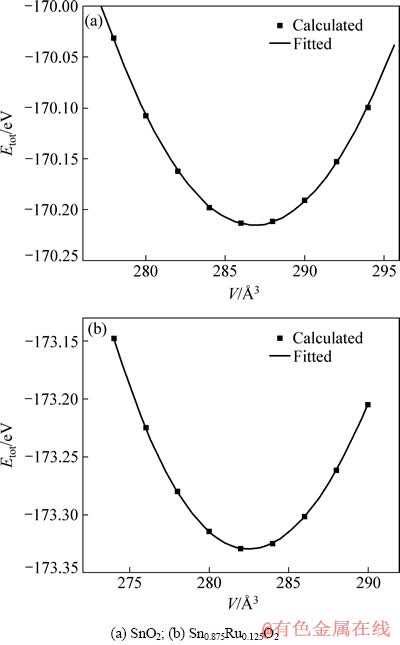
图2  两种体系的总能与超胞体积(E-V)关系曲线

Fig. 2  Dependence of total energy on average cell volume for two systems

表1  SnO₂、RuO₂和Sn_0.875Ru_0.125O₂的晶格参数

Table 1  Lattice parameters of SnO₂, RuO₂ and Sn_0.875Ru_0.125O₂

由表1可见，与SnO₂的晶胞体积相比，在SnO₂中掺入12.5%(摩尔分数)的Ru后晶胞体积变小，减小值为0.00095 nm³。晶胞的收缩与Ru离子半径(0.076 nm)小于Sn离子半径(0.083 nm^[15])有关。Sn_0.875Ru_0.125O₂仍然保持金红石的构型，这是由于RuO₂和SnO₂的点阵参数非常接近，以至满足了Hume-Rothery条件^[8]，因此，在添加少量Ru的SnO₂电极中，Ru⁴⁺离子可以取代Sn⁴⁺离子而形成固溶体，而前期研究^[13]也表明，包括Sn_0.875Ru_0.125O₂在内的更高Ru含量的电极材料中同样形成置换式固溶体。

2.2  能带结构和态密度

计算获得的SnO₂和Sn_0.875Ru_0.125O₂固溶体的能带结构如图3所示。需要注意的是，常规定义的费米能级在禁带的中部附近^[16]，而VASP软件所规定的费米能级则在价带顶部，即图3中零点为费米能级。由图3(a)中可见，未掺杂Ru的SnO₂能带结构中存在禁带，其帯隙宽度在高对称性的Γ点位置出现最小值，约为1.1 eV，与HU等^[4]计算的SnO₂完全相同，小于实验值(约为3.6 eV)^[17]。SnO₂帯隙的计算结果与实验结果存在一定偏差，这是计算方法本身造成的。如前述，本文作者采用LDA局域密度近似进行计算，而该方法常常低估原子和离子的基态能量，这样就导致带隙计算结果偏低，但用该方法计算的简便性和有效性已为大家普遍接受，对此文献中已有过讨论^{[6, 18-19]}。对照图3(a)和(b)可知，未掺杂Ru的本征态SnO₂难以导电；添加Ru后，在SnO₂晶格中形成了Ru离子取代型掺杂，引入了施主型杂质能级，材料呈现n型半导体特征。此代位杂质能级的宽度达到2.2 eV左右，与导带的低能部分几乎相连，导致带隙由1.1 eV降低至0.1 eV；同时还可以看出，Sn_0.875Ru_0.125O₂的费米能级已处于施主能级之中，因此材料呈现接近金属的简并半导电体。可见，Ru掺杂改变了SnO₂的导电状态和性质。

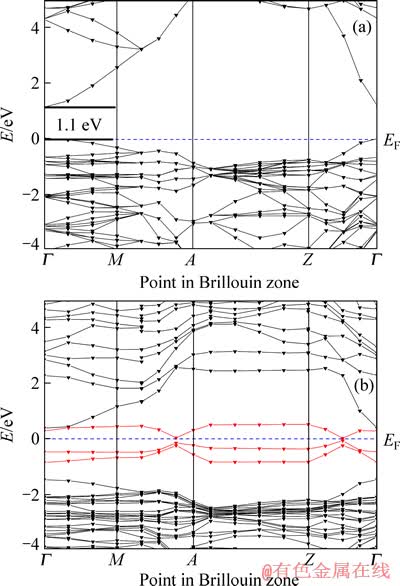
图3  SnO₂和Sn_0.875Ru_0.125O₂的能带结构图

Fig. 3  Band structures of SnO₂ (a) and Sn_0.875Ru_0.125O₂ (b)

为进一步分析添加Ru对SnO₂导电性质的影响，分别计算了SnO₂、Sn_0.875Ru_0.125O₂的总态密度和分波态密度，结果如图4所示。SnO₂的总态密度可分为5组峰，其中A、B和C峰属于价带， D和E峰属于导带，与NABI等^[20]计算所得到的结果非常接近。位于-15.9~18.9 eV 处的A峰主要是因O 2s和Sn 5p电子态发生轨道重叠，它属深能级处的内层轨道相互作用。从约-8.3 eV至价带顶存在B和C两组峰，其中的B峰主要来自于Sn 5s-O 2p电子杂化形成的成键态。而C峰主要表现为O 2p态特征。低能级部分对应的D组峰，主要为Sn 5s-O 2p杂化后的反键态。高能部分的E组峰主要是Sn 5p的电子态，另有少量的Sn 5s和O 2p电子态的贡献。

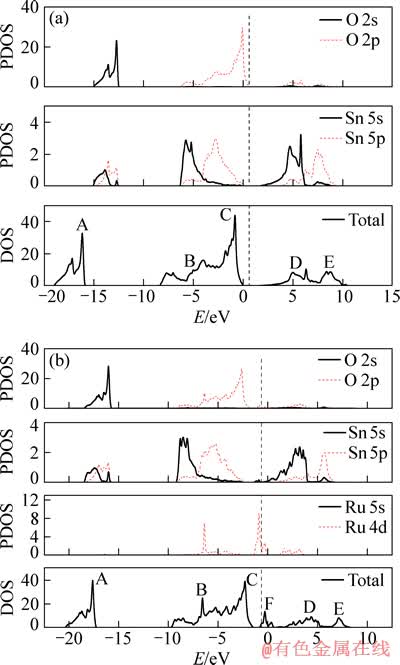
图4  SnO₂和Sn_0.875Ru_0.125O₂总态密度(DOS)和分波态密度(PDOS)

Fig. 4  DOS and PDOS of SnO₂ (a) and Sn_0.875Ru_0.125O₂ (b)

图4(b)所示为Sn_0.875Ru_0.125O₂固溶体的总态密度图和分波态密度分布。可以看出，Sn_0.875Ru_0.125O₂整个体系的态密度存在明显向低能方向移动的趋势，其中B和C两组峰移动的能量约为1.2 eV。由于Ru 5s参与了与O 2p的轨道杂化，略微改变了B峰的形态。值得注意的是，添加Ru离子后，Ru在导带底形成施主型的浅杂质能级(见图4(b)中的F峰)，它与导带底部只有0.1 eV的能隙，此代位杂质能级峰尖突出，说明其中做出主要贡献的Ru 4d电子态具有很强的局域特征。对图4(b)中电子的部分态密度经积分运算可得到，电子进入导带的相对电子数为2.7，说明掺杂Ru后，材料导带内电子数目明显增加，材料从本征态难以导电转变为带隙非常小之简并态半导体。这一掺杂贵金属引起的导电机制的变化现象，在SnO₂中加Pd^[21]和HfO₂中加Ru^[22]的材料中也有发现。

2.3  载流子浓度

对于导电材料来说，导电的关键是载流子的输运，它是由费米面附近的电子态所决定的^[23]。掺杂前后SnO₂载流子输运能力的不同还需从量的变化方面来分析。

因为Ru掺杂浓度为12.5%，属于高掺杂浓度，形成简并半导体，故电子服从费米-狄拉克分布：

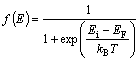                      (1)

式中：E_F为Fermi能级，E_i为导带底能级，k_B为波尔兹曼常数，T为热力学温度。体系的导带电子浓度(n₀)为

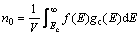                      (2)

式中：g_c(E)为导带底附近状态密度，V为超晶胞体积。通过对总态密度(见图4(b))的积分计算可得(积分区间从导带底到费米能级)，Sn_0.875Ru_0.125O₂的电子浓度为9.64×10²¹ cm^-3，而Ru掺杂前SnO₂的电子浓度为2.62×10¹⁸ cm^-3，掺杂后电子浓度增大了约4×10³ 倍，其中SnO₂的计算结果和文献报道的1×10¹⁵~1×10¹⁸ cm^-3[24-26]基本相符。根据载流子浓度计算结果，结合图3和图4可以发现，Sn_0.875Ru_0.125O₂的导电机制与SnO₂的相比，发生了显著改变，SnO₂为半导体，掺杂之后的Sn_0.875Ru_0.125O₂已经转变成为接近金属特性的简并态半导体，因而材料的导电性能显著增强。

3  结论

1) 对金红石型的SnO₂和Sn_0.875Ru_0.125O₂固溶体进行了第一性原理计算，对比分析了Ru掺杂前后SnO₂的晶体结构和电子结构。掺杂12.5%Ru后，其晶胞体积减小，同时Ru的掺入导致体系的态密度明显向低能方向移动，并且在SnO₂导带底附近形成施主型杂质能级，其与导带非常接近，使带隙由1.1 eV减小至0.1 ev，同时费米能级上移进入施主能级，使导电类型发生改变。经计算，掺杂后载流子浓度为9.64×10²¹ cm^-3，较掺杂前的增大4×10³倍，说明材料导电类型由半导体转变为接近金属的n型简并半导体。可见，添加少量的Ru便可极大地改善SnO₂电极材料的导电性能，这一研究结果阐释了掺杂Ru的SnO₂氧化物电极材料具有优良导电性能的物理基础，揭示了此类电极性能优越的物理本质，为制备与应用此类电极材料提供了理论依据。

REFERENCE

[1] 王 欣, 唐 电, 周敬恩. 添加SnO₂组元对RuO₂-TiO₂-SnO₂/Ti钛阳极组织形貌的影响[J]. 中国有色金属学报, 2002, 12(5): 920-924.

WANG Xin, TANG Dian, ZHOU Jin-en. Effects of SnO₂ on microstructure, morphology of RuO₂+SnO₂+TiO₂/Ti anode[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(5): 920-924.

[2] WANG Xin, TANG Dian, ZHOU Jin-en. Microstructure, morphology and electrochemical property of RuO₂70SnO₂30mol% and RuO₂30SnO₂70mol% coatings[J]. Journal of Alloys and Compounds, 2007, 430: 60-66.

[3] WU Xu, TAYAL J, BASU S, SCOTT K. Nano-crystalline Ru_xSn_1-xO₂ powder catalysts for oxygen evolution reaction in proton exchange membrane water electrolysers[J]. International Journal of Hydrogen Energy, 2011, 36: 14796-14804.

[4] HU Chi-chang, CHANG Kuo-hsin, WANG Chen-ching. Two-step hydrothermal synthesis of Ru-Sn oxide composites for electrochemical supercapacitors[J]. Electrochimica Acta, 2007, 52: 4411-4418.

[5] LEE J M, HAN S B, LEE Y W, SONG Y J, KIM J Y, PARK K W. RuO₂-SnO₂ nanocomposite electrodes for methanol electrooxidation[J]. Journal of Alloys and Compounds, 2010, 506: 57-62.

[6] STAMPFL C, VAN DE WALLE C G. Density-functional calculations for III-V nitrides using the local-density approximation and the generalized gradient approximation[J]. Physical Review B, 1999, 59: 5521-5535.

[7] WU Nae-lih, KUO Shin-liang, LEE Ming-hsueh. Preparation and optimization of RuO₂-impregnated SnO₂ xerogel supercapacitor[J]. Journal of Power Sources, 2002, 104: 62-65.

[8] NANNI L, POLIZZI S, BENEDETTI A, DE BATTISTI A. Morphology, microstructure, and electrocatalytic properties of RuO₂-SnO₂ thin films[J]. Journal of Electrochemical Society, 1999, 146: 220-225.

[9] ZHU Zhi-gang, RAMESH C D, ARUNABHIRAM C, RIADH S, HIDEYUKI T, MICHIHISA K, NOZOMU H, AKIRA E, HIROMITSU T, CARLOS A D C, MOMOJI K, AKIRA M. Enhanced gas-sensing behaviour of Ru-doped SnO₂ surface: A periodic density functional approach[J]. Journal of Physics and Chemistry of Solids, 2009, 70: 1248-1255.

[10] GODINHO K G, WALSH A, WATSON G W. Energetic and electronic structure analysis of intrinsic defects in SnO₂[J]. Journal of Physical Chemistry C, 2009, 113: 439-448.

[11] ZHU Jun-qiu, WANG Xin, YI Zhong-hua, TANG Zhong-zhi, WU Bo, TANG Dian, LIN Wei. Stability of solid-solution phase and the nature of phase separation in Ru-Zr-O ternary oxide[J]. Journal of Physical Chemistry C, 2012, 116: 25832-25839.

[12] WANG Xin, DENG Fen-yong, TANG Zhong-zhi, WU Bo, TANG Dian, LIN Wei. The nature of phase separation in a Ru-Sn-O ternary oxide electrocatalyst[J]. Phys Chemistry Chemical Physics, 2013, 15(11): 3977-3984.

[13] TANG Dian, WEN Shi-xue, CHEN Shi-ren. Preparation of RuO₂-SnO₂ nanomaterial by sol gel technique[J]. Transactions of Metal Heat Treatment, 2000, 10: 337-339.

[14] GRACIA L, BELTRAN A, ANDRES J. Characterization of the high-pressure structures and phase transformations in SnO₂: A density functional theory study[J]. Journal of Physical Chemistry B, 2007, 111: 6479-6485.

[15] MURAKAMI Y, ITO M, KAJI H, TAKASU Y. Surface characterization of ruthenium-tin oxide electrodes[J]. Applied Surface Science, 1997, 121: 314-318.

[16] 赵慧芳, 曹全喜, 李建涛. N、Ga共掺杂实现p型ZnO的第一性原理研究[J]. 物理学报, 2008, 57: 5828-5832.

ZHAO Hui-fang, CAO Quan-xi，LI Jian-tao. First principle study of N, Ga codoped P-type ZnO[J]. Acta Physica Sinica, 2008, 57: 5828-5832.

[17] DOLBEC R, KHAKANI M A E, SERVENTIA A M, TRUDEAU M, SAINT-JACQUES R G. Microstructure and physical properties of nanostructured tin oxide thin films grown by means of pulsed laser deposition[J]. Thin Solid Films, 2002, 419: 230-236.

[18] 逯 瑶, 王培吉, 张昌文, 冯现徉, 蒋 雷, 张国莲. 第一性原理研究Fe掺杂SnO₂材料的光电性质[J]. 物理学报, 2011, 60: 113101-113108.

LU Yao, WANG Pei-ji, ZHANG Chang-wen, FENG Xian-yang, JIANG Lei, ZHANG Guo-lian. First-principles calculation on electronic structure and optical properties of iron-doped SnO₂[J]. Acta Physica Sinica, 2011, 60: 113101-113108.

[19] PERDEW J P, LEVY M. Physical content of the exact kohn-sham orbital energies: Band gaps and derivative discontinuities[J]. Physical Review Letters, 1983, 51: 1884-1887.

[20] NABI Z, KELLO A, MECABIH S, KHALFI A, BENOSMAN N. Opto-electronic properties of rutile SnO₂ and orthorhombic SnS and SnSe compounds[J]. Materials Science and Engineering B, 2003, 98: 104-115.

[21] SKALA T, VELTRUSKA K, MOROSEAC M, MATOLINOVA I, CIRERA A, MATOLIN V. Redox process of Pd-SnO₂ system[J]. Surface Science, 2004, 566: 1217-1221.

[22] MUKHOPADHYAY A B, SANZ J F, MUSGRAVE C B. First-principles investigation of the structure, energetics, and electronic properties of Ru/HfO₂ interfaces[J]. Journal of Physical Chemistry C, 2007, 111: 9203-9210.

[23] 刘恩科, 朱秉升, 罗晋生. 半导体物理学[M]. 北京：国防工业出版社, 2008: 212-213.

LIU En-ke, ZHU Bing-sheng, LUO Jin-sheng. Physics semiconductor[M]. Beijing: National Defense Industry Press, 2008: 212-213.

[24] 郭玉忠, 王建华, 黄瑞安. 掺杂SnO₂透明导电薄膜电学及光学性能研究[J]. 无机材料学报, 2002, 17: 131-138.

GUO Yu-zhong, WANG Jian-hua, HUANG Rui-an. Electrical and optical properties of transparent and conductive Sb-doped SnO₂ films[J]. Journal of Inorganic Materials, 2002, 17: 131-138.

[25] SVANE A, ANTONCIK E. Electronic structure of rutile SnO₂, GeO₂ and TeO₂[J]. Journal of Physics and Chemistry of Solids, 1987, 48: 171-180.

[26] FREEMAN A J, POEPPELMEIER K R, MASON T O, CHANG R P H, MARKS T J. Chemical and thin film strategies for new transparent conducting oxides[J]. MRS Bull, 2000, 25: 45-51.

(编辑  龙怀中)

基金项目：国家自然科学基金资助项目(11374053，11104031，50971043，51171046)

收稿日期：2013-08-27；修订日期：2014-02-26

通信作者：唐  电，教授；电话：0591-22866532；E-mail：tangdian@fzu.edu.cn