预应力自平衡索桁架的非线性固有振动
杨立军1,叶柏龙2,喻爱南2,吴晓1
(1. 湖南文理学院 土木建筑工程学院,湖南 常德,415000;
2. 中南大学 土木建筑学院,湖南 长沙,410083)
摘要:研究预应力自平衡索桁架的非线性固有振动。考虑温度变化及几何非线性影响,采用连续化理论导出点支式玻璃幕墙预应力自平衡索桁架支承体系非线性振动方程。通过Galerkin方法,将偏微分程转化为常微分方程,采用L-P法对常微分方程进行求解。结合工程实例讨论分析温度变化、振幅、初始张力、矢高等因素对点支式玻璃幕墙预应力自平衡索桁架支承体系非线性振动的影响。算例结果表明:预应力自平衡索桁架支承体系固有频率随着温度的升高而减小,具有较强的非线性,其固有振动频率随着振幅发生变化,其非线性振动呈现“硬弹簧”特性,非线性振动频率高于线性振动频率。
关键词:预应力;自平衡索桁架;点支式玻璃幕墙;非线性;固有振动
中图分类号:TU394;O322 文献标志码:A 文章编号:1672-7207(2011)04-1111-06
Nonlinear natural vibration of prestressed self-balanced cable truss
YANG Li-jun1, YE Bai-long2, YU Ai-nan2, WU Xiao1
(1. College of Architecture & Civil Engineering, Hunan University of Arts and Science, Changde 415000, China;
2. School of Civil Engineering and Architecture, Central South University, Changsha 410083, China)
Abstract: The nonlinear natural vibration of prestressed self-balanced cable truss was investigated. Taking the temperature effect and geometric nonlinearity into consideration, the nonlinear vibration equation of prestressed self-balanced cable truss support system in point-supported glass curtain wall was derived by assuming the support system as a continuum membrane. By the Galerkin method, the partial differential equation was transformed into ordinary differential equation which was solved using L-P method. The effects of temperature, amplitude, initial tension and vector height on the nonlinear vibration were discussed using the engineering example. The result indicates that frequency of self-balanced cable truss support system decreases, which results in the increase of temperature, the vibration of self-balanced cable truss support system belongs to the nonlinear system, which is different from conventional structures, and its frequency varies with the amplitude of vibration, which shows hard spring characteristic. The nonlinear vibration frequency is higher than linear vibration frequency.
Key words: prestressing; self-balanced cable truss; point-supported glass curtain wall; nonlinearity; natural vibration
点支式玻璃幕墙是目前流行的玻璃幕墙建造技术,轻巧通透,构成形式灵活多变,在一些大型公共建筑物(如展览馆、机场候机楼、歌剧院等)中得到了广泛应用[1-2]。点支式玻璃幕墙由结构支承体系、驳接头和玻璃组成[3-4]。预应力自平衡索桁架是点支承玻璃幕墙的主要支承结构形式之一,如广州新白云国际机场主楼、连接楼的外围护点支式玻璃幕墙支承结构均采用了预应力自平衡索桁架[5]。预应力自平衡索桁架由中间主压杆、辅助横撑杆以及两侧布置的拉索组成。索的预拉力通过两端由主压杆来承担,从而在桁架内部形成一个独立的力平衡体系。在承受横向荷载时,相当于一个两端简支桁架的结构功能,故称为预应力自平衡索桁架。与普通的索桁架相比,预应力自平衡索桁架由于其本身独立形成一个力平衡体系,拉索的预拉力不施加在周边结构上,这就解决了大跨度拉索对周边结构附加拉力问题。现在对点支式玻璃幕墙预应力索桁架支承体系开展了非常多的研究[6-10],但基本上局限于其静力行为的研究。索桁架作为一种新型预张力结构体系,具有柔性大、质量小、阻尼小、自振频率低的特点,属风敏感结构,不能将传统的刚性结构动力计算方法直接用于该结构体系。关于柔性结构的动力学行为已经成为当今学术研究的热点,如吴丽丽等[11-20]研究了索结构的动力性能。作为自平衡索桁架结构风振分析的基础,本文作者考虑温度变化及几何非线性影响,采用连续化理论导出点支式玻璃幕墙预应力自平衡索桁架支承体系非线性固有振动方程。通过Galerkin方法,将偏微分程转化为常微分方程,采用L-P法对预应力自平衡索桁架支承体系非线性固有振动进行计算。
1 非线性固有振动方程
基本假定:(1) 拉索是理想柔性的;(2) 自平衡索桁架的横撑杆绝对刚性,横撑杆对上下拉索的力为连续分布;(3) 索材料满足虎克定律。
图1所示为预应力自平衡索桁架,其非线性振动方程为:
 (1)
(1)
 (2)
(2)
式中:下标1和2分别代表稳定索、承重索(下同);H为索初始水平张力;w为振动位移函数;ΔH为钢拉索水平拉力增量;z为索初始形状函数;m为索单位面积质量;q(x,t)为横撑杆给索的力。
将式(1)与式(2)相加,并令M=m1+m2,得:

 (3)
(3)

图1 预应力自平衡索桁架
Fig.1 Prestressed self-balanced cable truss
钢拉索的拉力增量ΔH1和ΔH2分别为
 (4)
(4)
式中:E为钢拉索弹性模量;αs为热膨胀系数;A为钢拉索单位长度横截面积;Δθ为温度增量。
设稳定索和承重索初始形状函数为:
 (5)
(5)
在实际应用中,往往对基频最感兴趣,设自平衡索桁架振动位移函数为
 (6)
(6)
由Galerkin方法可以得到:

 (7)
(7)
式中:中括号内为自平衡索桁架非线性振动方程;sin[π(x+l/2)/l]为振型函数。
将式(4)~(6)代入式(7),经整理可得:
 (8)
(8)
式中:T表征点的振动规律;

 ;
; ;
; ;
; 。
。
2 非线性固有振动近似解
式(8)是一个非线性方程,利用L-P法对式(8)求解。设式(8)的初始条件为
t=0, ,
, (9)
(9)
令 ,把式(8)化为
,把式(8)化为
 (10)
(10)
设
 (11)
(11)
将式(11)代入式(10),比较ε同次幂系数得:
 (12)
(12)
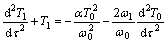 (13)
(13)

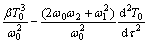 (14)
(14)
由式(12)可得:
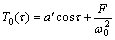 (15)
(15)
由式(9)和式(15)可得:
 (16)
(16)
把式(10)的各阶摄动项表示为系数待定的傅里叶级数,得

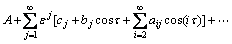 (17)
(17)
为了使式(17)满足式(9),需补充约束条件:
 (18)
(18)
将T0(τ)和T1(τ)的级数表达式代入式(13)和式(14),求得预应力自平衡索桁架支承体系非线性固有振动频率及位移函数分别为:


 (19)
(19)
 ?
?


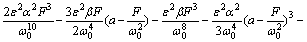



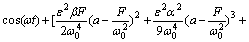


 (20)
(20)
3 算例分析及有限元计算验证
广州新白云国际机场酒店在正面入口选用了如图1所示的预应力自平衡索桁架点支式玻璃幕墙。点支式玻璃幕墙宽9 m,高12 m。索桁架间距2.7 m,跨度l=12 m,h1=h2=0.92 m。竖向索采用12 mm钢拉索,主压杆采用245 mm×6.5 mm(外径×壁厚)。承重索及稳定索呈抛物线布置,截面面积261.41 mm2。初始张拉力40 kN,αs=1.2×10-5/℃,E=150 GPa。索及玻璃幕质量M=80 kg/m2。得需要的基本参数为:H1=H2=14.8 kN/m,A1=A2=9.68×10-5 m。由此可得到预应力自平衡索桁架支承体系振动圆频率(ω0,ω),将振动圆频率除以2π得振动频率(f0,f),计算结果如表1和表2所示。
把以上有关参数代入式(19)和式(20),即可得到自平衡索桁架支承体系非线性固有振动的时程曲线,如图2所示x=0处时程曲线。
由式(19)也可以讨论其他因素对点支式玻璃幕墙自平衡索桁架支承体系振动特性的影响。
下面讨论初始张拉力的影响。初始拉力分别取上面算例的0.8倍、1.0倍和1.2倍。
工况1: ;
;
工况2: ;
;
工况3: 。
。
取振幅a=0.1 m,其他参数不变,据此可以得到初始张拉力对自平衡索桁架支承体系非线性固有振动频率影响,如表3所示。
取振幅a=0.1 m,设h=h1=h2为1.0,1.5和2.0 m,其他参数不变,据此讨论矢高 对自平衡索桁架非线性固有振动频率影响,如表4所示。
对自平衡索桁架非线性固有振动频率影响,如表4所示。
为验证本文近似公式的可靠性,采用ANSYS对算例中索桁架支承体系进行了瞬态分析,按表2给定的振幅a和温度增量Δθ参数分别计算索桁架支承体系固有频率。索桁架初始张拉力和温度增量通过钢拉索初始应变模模拟。非线性瞬态分析的激振方式为初始位移法,即先按照振型形状 给索桁架各节点施加瞬时位移,然后释放让其自由振动。表2中f和f′分别为本文中的式(19)和ANSYS计算结果。
给索桁架各节点施加瞬时位移,然后释放让其自由振动。表2中f和f′分别为本文中的式(19)和ANSYS计算结果。
表1 索桁架线性振动固有频率
Table 1 Linear vibration frequency of cable truss Hz

表2 本文计算结果与有限元解的比较
Table 2 Results comparison between this work and ANSYS

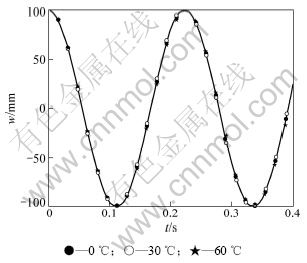
图2 温度对时程曲线的影响
Fig.2 Influence of temperature on time-history curve
表3 初始拉力对非线性振动固有频率的影响
Table 3 Influence of initial tension on nonlinear frequency Hz

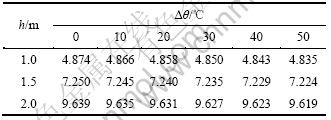
表4 矢高对非线性振动固有频率的影响
Table 4 Influence of vector height on nonlinear frequency Hz
对表1~4及图2进行分析可以得到如下结论:
(1) 本文给出的解析解计算结果和有限元计算结果吻合较好,小于工程上的允许误差(5%),验证了该公式的可靠性(见表2)。
(2) 温度变化对结构时程曲线影响不大,这说明了索桁架振动对温度变化不敏感(见图2)。
(3) 自平衡索桁架支承体系线性振动固有振动频率随着温度的增加而减小。如表1所示,当温度增量Δθ=0 ℃时,索桁架线性振动频率f0=4.489 Hz;当Δθ=50 ℃时,f0=4.447 Hz,频率降低了0.94%。
当振幅一定时,随着温度的增加,自平衡索桁架支承体系非线性固有振动频率将变小;如表2所示,振幅a=0.15 m,当温度增量Δθ=0 ℃时,索桁架非线性振动频率f=4.504 Hz;当Δθ=40 ℃时,f=4.471 Hz,频率降低了0.73%。
(4) 当温度一定时,随着振幅的增大,自平衡索桁架支承体系非线性固有振动频率将增大。如在表2中,温度增量Δθ=20 ℃时,振幅a为0.05,0.15和0.25 m的索桁架非线性振动频率f分别等于4.474,4.488和4.515 Hz,频率分别升高了0.31%和0.92%。这说明自平衡索桁架支承体系非线性振动呈现“硬弹簧”特性。
(5) 自平衡索桁架支承体系的非线性振动频率高于线性频率。如温度增量Δθ=20 ℃时,f0=4.472 Hz,f=4.488 Hz(a=0.15 m),频率升高0.36%。与一般结构不同,由于自平衡索桁架支承体系在振动过程中索力不断变化导致其刚度变化,故实际上它属于非线性硬化刚度体系。
(6) 索桁架振动频率随着初始拉力增大而增大,但增大效果不明显。如Δθ=20 ℃时工况2、工况3的振动频率相对于工况1分别升高0.31%和0.63%(见表3)。这也印证了有关文献初始拉力对索桁架支承体系的刚度贡献不大的结论[6]。
(7) 自平衡索桁架支承体系振动频率随着矢高增大而增大,并且增大幅度很大,这与文献[21]的结论是一致的。如温度增量Δθ=30 ℃时,矢高h为1.0,1.5和2.0 m的非线性振动频率f分别等于4.850,7.235和9.627 Hz,频率分别升高了49.18%和98.49%(见 表4)。
4 结论
(1) 考虑温度变化及几何非线性影响,采用连续化理论导出了点支式玻璃幕墙预应力自平衡索桁架支承体系非线性振动方程。采用L-P法求得了振动方程近似解,据所得到的近似解可以方便地分析各种因素对其动力特性的影响。
(2) 本文给出的点支式玻璃幕墙预应力自平衡索桁架支承体系非线性振动解析解计算结果与有限元计算结果较吻合,小于工程上的允许误差,验证了该解析解的可靠性。
(3) 预应力自平衡索桁架支承体系固有频率随着温度的增加而减小,随着振幅、初始拉力、矢高的增大而增大。
(4) 自平衡索桁架支承体系的非线性振动频率高于线性振动频率。
参考文献:
[1] Graf H, Albrecht G, Sackmann V, et a1. Structural behaviour of point-supported and clamped laminated glass[J]. Structural Engineering International, 2004, 14(2): 129-133.
[2] Schlaich J, Schober H, Moschner T. Prestressed cable net facades[J]. Structural Engineering International, 2005, l5(1): 36-39.
[3] Vyzantiadou M, Avdelas A. Point fixed glazing systems: technological and morphological aspects[J]. Journal of Constructional Steel Research, 2004, 60(6): 1227-1240.
[4] 吴丽丽, 王元清, 石永久, 等. 点支式玻璃建筑单层索网体系的动力特性[J]. 清华大学学报: 自然科学版, 2006, 46(3): 318-321.
WU Li-li, WANG Yuan-qing, SHI Yong-jiu, et al. Dynamic characteristics of monolayer cable net for dot point glass curtain wall[J]. Journal of Tsinghua University: Science and Technology, 2006, 46(3): 318-321.
[5] 花定兴, 姚裕昌. 广州新机场主航站楼点支式玻璃幕墙结构设计[J]. 建筑结构, 2003, 33(11): 67-72.
HUA Ding-xing, YAO Yu-chang. Design and analysis of the point supported glass curtain wall in the Guangzhou new airport[J]. Building Structure, 2003, 33(11): 67-72.
[6] 毛文俊, 刘锡良. 大跨度典型索桁架支承结构体系的受力性能研究[J]. 工业建筑, 2008, 38(2): 96-98.
MAO Wen-jun, LIU Xi-liang. Study on load-bearing behavior of large-span typical cable truss supporting structural system[J]. Industrial Construction, 2008, 38(2): 96-98.
[7] 殷永炜, 张其林, 王丹, 等. 点支式玻璃幕墙索桁架支承体系的结构性能研究[J]. 结构工程师, 2005, 21(2): 17-21.
YIN Yong-wei, ZHANG Qi-lin, WANG Dan, et al. Study on load-bearing behavior of cable truss support system in point-supported curtain walls[J]. Structural Engineers, 2005, 21(2): 17-21.
[8] 王永焕, 徐海翔, 徐天爽. 北京长安中心点式玻璃幕墙工程索桁架静载试验[J]. 钢结构, 2007, 22(8): 4-7.
WANG Yong-huan, XU Hai-xiang, XU Tian-shuang. Static load test of prestress cable truss for point-supported glass curtain wall of Beijing Changan center[J]. Steel Construction, 2007, 22(8): 4-7.
[9] 郭彦林, 郭宇飞. 预应力自平衡索桁架的承载性能研究[J]. 空间结构, 2008, 14(3): 41-46.
GUO Yan-lin , GUO Yu-fei. Behavior of prestress self-balanced cable trusses[J]. Spatial Structures, 2008, 14(3): 41-46.
[10] 杨立军, 叶柏龙, 喻爱南. 点式幕墙索桁架支撑体系结构判定分析[J]. 四川建筑科学研究, 2005, 31(5): 29-31.
YANG Li-jun, YE Bai-long, YU Ai-nan. Analysis on the judge of cable truss system of point supported curtain wall[J]. Sichuan Building Science, 2005, 31(5): 29-31.
[11] 吴丽丽, 王元清, 石永久. 点支式玻璃建筑单层索网体系的动力特性分析[J]. 重庆建筑大学学报, 2006, 28(3): 39-42.
WU Li-li, WANG Yuan-qing, SHI Yong-jiu. Analysis on dynamic properties of monolayer cable net for point-supported glass curtain wall[J]. Journal of Chongqing Jianzhu University, 2006, 28(3): 39-42.
[12] 吕建根, 赵跃宇, 王荣辉. 索拱组合结构的动力建模及其内共振分析[J]. 中南大学学报: 自然科学版, 2010, 41(1): 316-321.
L? Jian-gen, ZHAO Yue-yu, WANG Rong-hui. Dynamical modeling and internal resonance of cable-stayed arch structure[J]. Journal of Central South University: Science and Technology, 2010, 41(1): 316-321.
[13] 杨立军, 吴晓, 叶柏龙, 等. 大跨索网结构动力特性[J]. 四川大学学报: 工程科学版, 2010, 42(6): 85-90.
YANG Li-jun, WU Xiao, YE Bai-long, et al. Dynamic characteristics of long-span cable-net structures[J]. Journal of Sichuan University: Engineering Science Edition, 2010, 42(6): 85-90.
[14] 武岳, 冯若强, 沈世钊. 单层索网幕墙结构的风振响应分析及实用抗风设计方法[J]. 计算力学学报, 2007, 24(5): 633-637.
WU Yue, FENG Ruo-qiang, SHEN Shi-zhao. Wind-induced response analysis and practical wind-resistant design method of cable net glazing[J]. Chinese Journal of Computational Mechanics, 2007, 24(5): 633-637.
[15] 尚仁杰, 李谦, 吴转琴, 等. 基于最小能量原理的矩形平面预应力索网结构大变形自由振动研究[J]. 振动与冲击, 2007, 26(9): 158-161.
SHANG Ren-jie, LI Qian, WU Zhuan-qin, et al. Study on the free vibration of the rectangle two-layer prestress cable net with large displacement basing on least energy principle[J]. Vibrate and Shock, 2007, 26(9): 158-161.
[16] Martine L, Perotti F. Numerical analysis of the nonlinear dynamic behavior of suspended cables under turbulent wind excitation[J]. International Journal of Structural Stability and Dynamics, 2006, 13(3): 207-233.
[17] Kwan A. A simple technique for calculating natural frequencies for geometrically nonlinear prestressed cable structure[J]. Computer and Structure, 2005, 79(3): 41-50.
[18] Feng R Q, Wu Y, Shen S Z. Simplified calculation method of nonlinear frequency of cable net under mean wind load[J]. Acta Mechanica Solida Sinica, 2006, 19(3): 248-254.
[19] Chen B, Wu Y, Shen S Z. A new method for wind induced response analysis of long span roofs[J]. International Journal of Space Structures, 2006, 21(2): 93-101.
[20] Zhu Z H, Meguid S A. Nonlinear FE-based investigation of flexural damping of slacking wire cables[J]. International Journal of Solids & Structures, 2007, 44(16): 5122-5132.
[21] 何志鹃, 陆守明. 点支式玻璃幕墙索桁架支承体系自振特性算例及分析[J]. 四川建筑科学研究, 2007, 33(1): 38-41.
HE Zhi-juan, LU Shou-ming. Study on model-frequency behavior of cable truss support systems for dot point glass curtain[J]. Sichuan Building Science, 2007, 33(1): 38-41.
(编辑 杨幼平)
收稿日期:2010-04-18;修回日期:2010-08-27
基金项目:国家创新基金支持项目(08C26224301132);湖南“十一五”重点建设学科资助项目(湘教通[2006]180号);湖南省普通高校青年骨干教师项目(湘教通[2007]256号);湖南省科技计划项目(2008FJ3067)
通信作者:杨立军(1976-),男,湖南邵阳人,硕士,副教授,从事建筑结构理论研究和教学工作;电话:15873665127;E-mail:yanglj9601@163.com