7055铝合金中低比例动态再结晶的模拟
来源期刊:中国有色金属学报(英文版)2021年第7期
论文作者:李佳宸 吴晓东 廖斌 蔺晓敏 曹玲飞
文章页码:1902 - 1915
关键词:动态再结晶;JMAK模型;DEFORM-3D;7055铝合金;热压缩
Key words:dynamic recrystallization; JMAK model; DEFORM-3D; 7055 aluminum alloy; hot compression
摘 要:研究7055铝合金在温度为390~470 °C 和应变速率为0.01~1 s-1条件下热变形和动态再结晶行为。电子背散射衍射(EBSD)表征结果表明,7055铝合金在热变形下动态再结晶含量较低,动态再结晶含量为1%~13%。为了模拟低比例动态再结晶问题,对JMAK动态再结晶模型进行修正。应用修正的模型,结合商业有限元软件DEFORM-3D,对7055铝合金的热压缩过程进行数值模拟,模拟得到的动态再结晶比例和晶粒尺寸的平均绝对相对误差(AARE)分别为13.7%和6.3%,与实验结果吻合良好。为了进一步证实该模型的有效性,采用该方法对7055铝合金工业化热轧过程进行模拟,模拟结果表明热轧板的动态再结晶分布不均匀,与实验观察结果一致。
Abstract: The hot deformation and dynamic recrystallization (DRX) behaviors of 7055 aluminum alloy were studied at temperatures of 390-470 °C and strain rates of 0.01-1 s-1. A low DRX fraction between 1% and 13% was observed by using EBSD technique. A modified JMAK-type DRX model was proposed for such low DRX fraction problems. The model was used together with commercial FEM software DEFORM-3D to simulate the hot compression of 7055 aluminum alloy. There was a good agreement between experimental and predicted DRX fractions and grain size with an average absolute relative error (AARE) of 13.7% and 6.3%, respectively. In order to further verify the validity of the proposed model, the model was also used to simulate DRX in industrial hot rolling of 7055 aluminum alloys. The results showed that the distribution of DRX fraction was inhomogeneous, and agreed with experimental observations.
Trans. Nonferrous Met. Soc. China 31(2021) 1902-1915
Jia-chen LI1, Xiao-dong WU1, Bin LIAO2, Xiao-min LIN1, Ling-fei CAO1,3
1. International Joint Laboratory for Light Alloys (Ministry of Education), College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China;
2. Alnan Aluminium Co., Ltd., Nanning 530031, China;
3. Shenyang National Laboratory for Materials Science, Chongqing University, Chongqing 400044, China
Received 18 July 2020; accepted 28 January 2021
Abstract: The hot deformation and dynamic recrystallization (DRX) behaviors of 7055 aluminum alloy were studied at temperatures of 390-470 °C and strain rates of 0.01-1 s-1. A low DRX fraction between 1% and 13% was observed by using EBSD technique. A modified JMAK-type DRX model was proposed for such low DRX fraction problems. The model was used together with commercial FEM software DEFORM-3D to simulate the hot compression of 7055 aluminum alloy. There was a good agreement between experimental and predicted DRX fractions and grain size with an average absolute relative error (AARE) of 13.7% and 6.3%, respectively. In order to further verify the validity of the proposed model, the model was also used to simulate DRX in industrial hot rolling of 7055 aluminum alloys. The results showed that the distribution of DRX fraction was inhomogeneous, and agreed with experimental observations.
Key words: dynamic recrystallization; JMAK model; DEFORM-3D; 7055 aluminum alloy; hot compression
1 Introduction
7xxx aluminum alloys have been widely used in the aviation, aerospace, transportation and other industrial fields due to their high strength, excellent corrosion resistance, and low density [1]. Hot deformation is generally needed to form aluminum alloys into final products. During this process, the dynamic recovery (DRV) and the dynamic recrystallization (DRX) happen, and show the significant influence on the microstructure of the final products [2,3]. Precise control of deformation parameters is necessary for the control of DRV and DRX during hot deformation to obtain desired microstructure, and thereafter good mechanical properties. In order to find optimum deformation parameters, a reliable DRX model is needed to predict the microstructure of products.
Various DRV/DRX models have been proposed [4,5] considering different DRX mechanisms. One type of these are empirical models, which are purely based on experimental observations. In these models, the stress is defined as a function of temperature, strain and strain rate. DRV model is mainly based on the dislocation density model proposed by ESTRIN and MECKING [6], while Johnson-Mehl-Avrami- Kolmogorov (JMAK or Avrami) type model is often used to simulate the DRX [7-11]. Based on the Avrami’s work [7], SAITO [11] adopted the JMAK model in the following form:
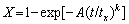 (1)
(1)
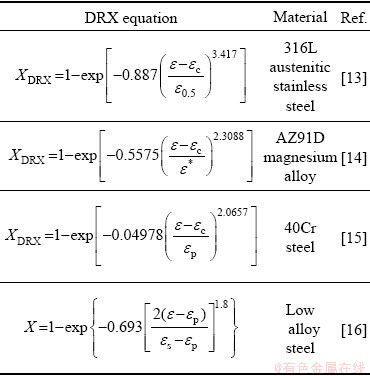
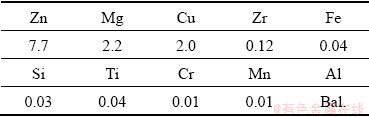
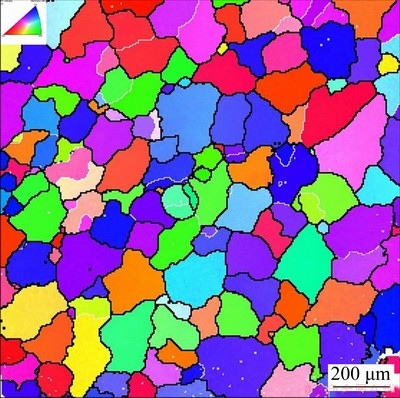
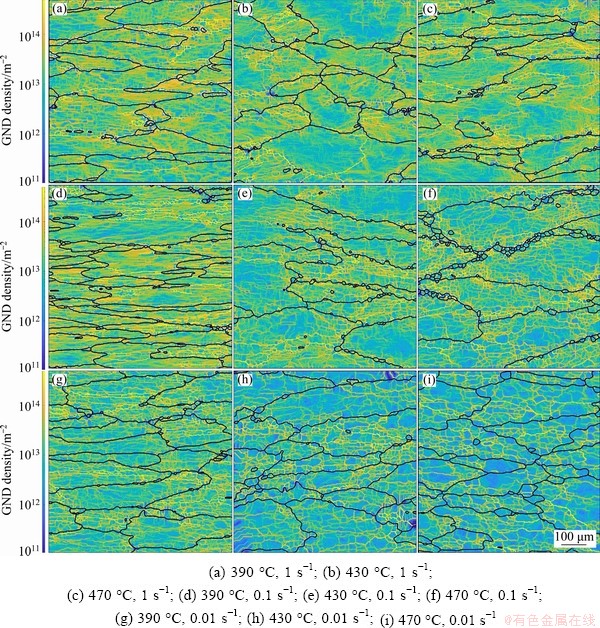
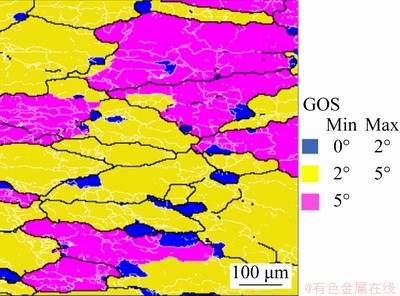
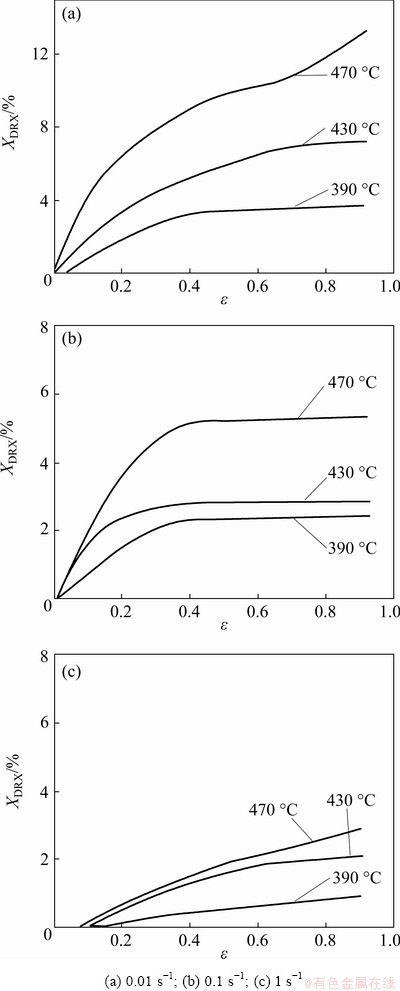
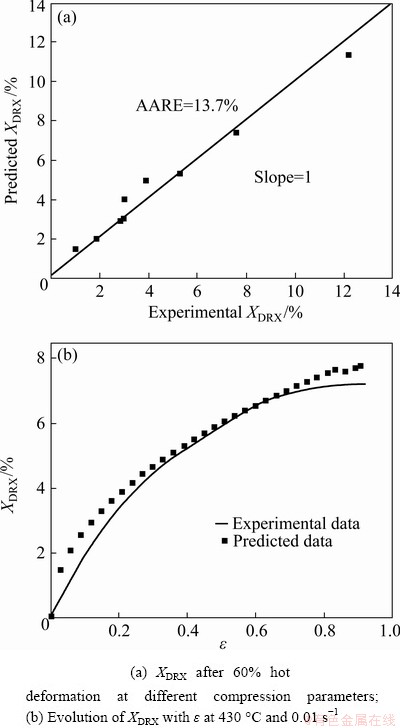
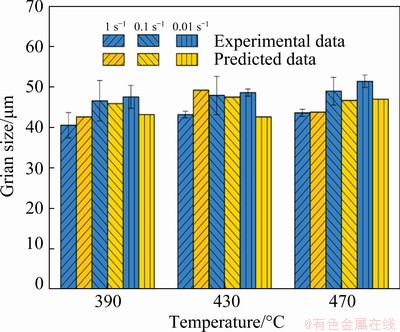
where X is the volume fraction of recrystallized grains, A and k are constants, t is the time, and tx is the time to a certain recrystallization fraction x (0 where XDRX is the DRX fraction, βd and kd are material constants, ε is the strain, εc is the critical strain where DRX starts, and εr is a reference strain [12]. WANG et al [13] adopted the strain for 50% fraction of DRX (ε0.5) as εr, and used the model to estimate accurately the volume fractions of DRX in 316LN austenitic stainless steel during hot deformation process. XU et al [14] found that there was a good consistency between the JMAK model and microstructure observation results using the strain for maximum softening rate (ε*) as εr in AZ91D magnesium alloy. Similar result was obtained by CHEN et al [15] using the peak strain (εp) in 40Cr steel. Based on εp, MIRZAEE et al [16] modified JMAK model with the steady state strain minus peak strain (εs-εp) as εr to predict the DRX flow curves at temperatures higher than 1000 °C in low alloy steel. Table 1 Various JMAK-type DRX equations However, HADADZADEH et al [12] found that the accuracy of Avrami DRX and Avrami SRX models was greatly reduced when the recrystallization fraction was lower than 50%, and the models even cannot be applied if the recrystallization fraction was too low when they were used to simulate the hot deformation of ZK60 alloy. This means that the current JMAK models mainly deal with materials with high DRX fraction during hot deformation. The reliability and capacity of these JMAK-type models will be greatly reduced if they are used to work on materials with low DRX fraction, for example, 7xxx series aluminum alloys. The DRX fraction of 7xxx aluminum alloys during hot deformation is generally very low [4,17] because 7xxx aluminum alloys have a large number of precipitates, which can strongly retard DRX by inhibiting the motion of grain boundaries; while DRV can occur easily due to high stacking fault energy of aluminum matrix, which reduces the driving force for DRX. LIAO et al [1] found that the main softening mechanism during hot deformation of 7050 aluminum alloy was DRV, and the fraction of DRX was very limited. ZANG et al [17] reported the fraction of DRX in Al-7.9Zn-2.7Mg-2.0Cu alloy was lower than 12% at the temperatures of 300-450 °C and the strain rates of 0.001-1 s-1. LI et al [18] reported the highest fraction of recrystallization was 10.2% in 7085 aluminum alloy. In order to simulate the hot deformation of 7xxx aluminum alloys, current JMAK models need to be modified. In this work, 7055 aluminum alloy was researched as a typical material with low proportion of DRX. A modified JMAK DRX model was proposed for low DRX fraction (XDRX) problems. The proposed model was applied in the finite element method (FEM) software DEFORM-3D to simulate hot compression of 7055 aluminum alloy and calculate the fraction of DRX, as well as the grain size. Finally, industrial hot rolling of 7055 aluminum alloy was simulated to further verify the proposed model, and the DRX fraction after hot rolling was calculated and compared with experimental observations. 2 Experimental The chemical composition of the studied 7055 aluminum alloy is shown in Table 2. The alloy was manufactured by the semi-continuous casting to approximate dimensions of 4000 mm × 500 mm × 400 mm. Before hot compression, the samples were homogenized at 460 °C for 3 h and 470 °C for 1 h. The microstructure of the homogenized sample is shown in Fig. 1. It has equiaxed grains with a grain size about 120 μm. Table 2 Chemical composition of alloy (wt.%) Fig. 1 Orientation map of heat-treated sample Cylindrical compression samples with 8 mm in diameter and 12 mm in height were used for the isothermal compression tests. Hot deformation was performed on a Gleeble-3800 thermal simulation machine. The specimens were heated to the deformation temperature at the heating rate of 2.5 °C/s and held for 3 min before compression to ensure uniform temperature distribution. The samples were compressed at temperatures of 390, 430, and 470 °C, and strain rates of 0.01, 0.1, and 1 s-1 with a reduction in height of 60%, corresponding to a true strain of 0.9. During the compression process, lubricant was used to reduce the friction between the mold and samples. After compression, the samples were quenched into water immediately to reserve the microstructure after compression. The samples were cut into halves along the direction parallel to the compression direction. The electron backscatter diffraction (EBSD) observations were carried out in the middle area of the cut surface. The EBSD samples were electro-polished in an electrolyte solution of 10% HClO4 and 90% C2H5OH at 20 V for 15 s. The EBSD characterization was carried out on a TESCAN MIRA 3 instrument using a scanning step length from 0.2 to 2.8 μm depending on the grain and subgrain size of the samples. Channel 5 software and MTEX software [19] were used to analyze the EBSD data. Finally, the finite element software DEFORM-3D was used to simulate the XDRX results. 3 Results and discussion 3.1 Flow behavior Figure 2 shows the true stress-true strain curves in different hot compression conditions. A gradual decrease of stress with increasing strain after the initial work hardening stage during plastic deformation can be observed in most of the curves, which is the result of dynamic softening caused by DRX and DRV. However, at lower deformation temperatures and higher strain rate (390 and 430 °C in Fig. 2(a)), a gradual increase of flow stress with increasing strain can be observed because the effect of work hardening was higher than that of dynamic softening [20]. Figure 2(d) shows the temperature changes at a strain rate of 1 s-1, where the samples’ temperature changes significantly at a high strain rate during deformation due to the heat induced by mechanical work. The flow stress strongly depends on the temperature, i.e., drops as the temperature increases, while it rises as the temperature decreases. In order to obtain the true stress-strain curves at constant temperatures, which are needed for FEM simulation, the experimental stress-strain curves need to be corrected to remove the influence of temperature change. The correction can be made using following equation [21]: where σc is the corrected flow stress, σuc is the experimental flow stress, Fig. 2 True stress-true strain curves of 7055 alloy compressed at 1 s-1 (a), 0.1 s-1 (b), 0.01 s-1 (c), variation of experimental temperatures at strain rate of 1 s-1 and different setting temperatures (d), and stress-strain curves after temperature correction (e) 3.2 Microstructure Fig. 3 EBSD maps of isothermal compression samples under different conditions Figure 3 shows the EBSD maps of the isothermal compression samples. The grey lines are subgrain boundaries with the misorientation angle between 2° and 15°, and black lines are grain boundaries with misorientation higher than 15°. The microstructure exhibits a typical feature of deformed grains, i.e., the grain is elongated perpendicularly to the compression direction. Some shear bands can be observed in the samples deformed at a higher strain rate, as shown in the white circles in Figs. 3(a) and (b), which is the typical characteristic of unstable deformation. It can also be observed that some small grains are located at the triple junctions (shown in white rectangle) or surrounded by deformed grains boundaries (shown in black rectangle), which are typical features for DRX. DRX grains can be observed in all graphs, as indicated by black arrows. The proportion of DRX grains and DRX grain size increase with the increase of isothermal compression temperature and decrease with the increase of the strain rate [22-24]. Many subgrain boundaries can be observed in Fig. 3, which are the evidence of DRV, suggesting that DRV is the main softening mechanism in all samples. DRX and DRV are competing processes because both of them are driven by the stored deformation energy. Aluminum alloys are high stacking fault energy materials. Dislocations can easily glide, climb and cross slip into partial dislocations, which favors DRV, and thereafter reduces the stored energy and retards DRX [4]. Moreover, the addition of alloying elements in 7xxx aluminum alloys is very high, which can form a large number of precipitates. These precipitates, especially Al3Zr precipitates in Zr alloyed Al-Zn-Mg-Cu alloys, can produce strong Zener pinning force on grain boundaries, which also inhibits DRX. Therefore, the fractions of DRX will be very low in the experimental alloys (1.28%-12.9%), even if the materials are deformed at high temperature and low strain rate. The density of geometrically necessary dislocation (GND) of all compressed samples was calculated based on EBSD results by MTEX, which was an open-source free MATLAB toolbox for EBSD data analysis [25]. The results are shown in Fig. 4. The density of dislocations is very high near the grain and sub-grain boundaries and gradually decreases with the increase of distance from grain and sub-grain boundaries, which suggests that grain boundaries are the main obstacles for the dislocation movement during hot deformation. With the increase of temperature and the decrease of strain rate, the density of GND gradually reduces. This can be attributed to DRV. Due to the DRV, the dislocations are aligned to compose a network, and part of the dislocation walls form sub-grain boundary. At higher temperature and lower strain rate (for example, 0.01 s-1 and 470 °C in Fig. 4(i)), larger recrystallized grains can be observed, of which the dislocation density is very low. But for the small recrystallized grains (Fig. 4(f)), some have low dislocation density, while others have high dislocation density. The deformed grains with higher dislocation density may be served as nucleation sites for recrystallization. Fig. 4 GND maps of isothermal compression samples under different conditions The DRX begins to nucleate when the dislocation density reaches the critical dislocation density, ρc, which can be calculated by the following equations [26-30]: where γi is the grain boundary energy, σs is the saturated flow stress, b is the modulus of Burger’s vector component, μ is the shear modulus, K is a constant about 10 for most metals, and M is the velocity of grain boundary movement. μ and M can be expressed by where μ0 represents the shear modulus at room temperature, Tm is the material’s melting temperature, k is the Boltzmann constant, λ is the thickness of characteristic grain boundary, Db is the boundary self-diffusion coefficient, Qb is the activation energy (69762 J/mol), and R is the mole gas constant (8.314 J/(mol·K)). The values of ρc in different deformation conditions were calculated using the parameters listed in Table 3 [28,29], and the calculated results are shown in Fig. 5(a). It can be noticed that ρc decreases with increasing deformation temperature and decreasing strain rate. The average dislocation density of the compressed samples is calculated as well according to Fig. 4, and shown in Fig. 5(b). The dependence of average dislocation density on deformation parameters is similar to that of ρc. Most values of the average dislocation density are higher than the corresponding ρc shown in Fig. 5(a), suggesting that DRX can happen under these deformation conditions. However, the average dislocation density is lower than the corresponding ρc for the samples deformed at a strain rate of 1 s-1, suggesting that in these deformation conditions DRX is hard to happen. These results correspond to the EBSD observations, of which the DRX fractions are very low in the samples deformed at strain rate of 1 s-1 (Fig. 3(a-c)). Table 3 Material parameters for 7055 aluminum alloy [28,29] 3.3 DRX fraction In order to calculate the fraction of DRX grains, grain orientation spread (GOS) was introduced to calculate XDRX. GOS represents the average deviation between the orientation of each point in a given grain and the average orientation of that grain [31,32]. The grain with threshold degree of GOS≤2° [33,34] can be defined as recrystallized grain. An example of GOS map is shown in Fig. 6, in which blue color areas (≤2°) are recrystallized grains, the yellow color areas (2°-5°) and the pink color areas (≥5°) are recovered and deformed grains, respectivley. The fraction of DRX can then be calculated according to the area fraction of the blue color area. Fig. 5 Critical dislocation density (a) and average dislocation density (b) under different deformation conditions Fig. 6 GOS map of sample deformed at 470 °C and 0.01 s-1 LAASRAOUI and JONAS [35] proposed the following equation to calculate the XDRX at a given true strain ε: where σ is the stress at a given true stain ε, σsat and σss are the saturated stress of DRV and DRX, respectively. σsat can be determined on the work hardening rate θ (=dσ/dε) vs σ curve. A typical θ-σ plot is shown in Fig. 7 for the sample compressed at a temperature of 430 °C and a strain rate of 0.01 s-1. In Fig. 7, the inflection point is defined as the onset of DRX, and the stress and strain at the inflection point are εc and σc (critical stress), respectively. σsat can be determined as the horizontal intercept of the tangent line of θ-σ curve through the inflection point with θ=0. Fig. 7 θ-σ curve at 430 °C and 0.01 s-1 (r is coefficient of DRV at a given temperature and strain rate) If a sample is fully crystallized after hot deformation, σss can be easily determined as final stress [14]; if a sample is not fully crystallized, σss is usually determined by extrapolation method. However, if the recrystallized fraction is too low, negative σss might be acquired sometimes, which is meaningless. Therefore, Eq. (7) needs to be modified in the current case. The DRX fraction in a given experimental deformation condition can be determined by microstructure characterization. According to Eq. (7), Xexp can be expressed by where σexp is the true stress at the maximum strain, Xexp and σexp are the DRX fraction and stress at a true strain of 0.9, a given deformation temperature and strain rate in this work, respectively. Substituting Eq. (8) into Eq. (7), the following expression can be acquired: Then, the dependence of XDRX on ε can be obtained using Eq. (9) and the experimental stress-strain curves, which is shown in Fig. 8. Fig. 8 DRX fraction as function of strain under different deformation conditions 3.4 DRX and cellular automation (CA) kinetic models 3.4.1 DRX kinetic model Due to the low DRX fraction in the current work, ε0.5, the strain at DRX fraction of 50%, cannot be acquired experimentally. Therefore, ε0.01, the true strain at DRX fraction of 1% is used as the reference strain, because all experimental DRX fractions are higher than 1%. Then, the JMAK model can be modified as The way to obtain εc is already shown in Fig. 7. By fitting the curves in Fig. 8 with Eq. (10), βd and kd can be obtained, which are 0.03 and 0.5, respectively. Therefore, the modified DRX kinetics equations of the studied samples can be expressed as 3.4.2 Simulation of DRX during hot compression Commercial DEFORM-3D software was used to simulate the hot compression of 7055 aluminum alloy cylinder at temperatures of 390, 430, and 470 °C, and strain rates of 0.01, 0.1, and 1 s-1 with a reduction ratio of 60% [36]. The developed DRX kinetic model was embedded in software DEFORM-3D to calculate XDRX in the middle of the samples, and was compared with experimental results, as shown in Fig. 9(a). It can be seen that the calculated results agree well with the EBSD results, and the average absolute relative error (AARE) is only 13.7%. Figure 9(b) shows the evolution of XDRX with strain at 430 °C and 0.01 s-1, which also has a good agreement with the experimental XDRX. Hence, it is evident that the modified JMAK model can simulate the DRX in 7055 aluminum alloy very well. 3.4.3 Grain size modeling by cellular automation Fig. 9 Comparison between experimental and predicted XDRX after hot compression The grain size was calculated using the CA module in the DEFORM-3D software. Laasroui-Jonas model was used to calculate the evolution of dislocations, in which the change of dislocation density ρ relative to the change of ε was expressed as [37,38] where h is the work-hardening rate. h and r can be described as follows: where Figure 10 shows the change of stress vs strain rate on logarithm scale for the studied alloy at different true strains of 0.3, 0.6 and 0.9, respectively. m is the slope of the lines. The value of r can be determined from Fig. 7 [37], and h can be calculated as The value of α is 0.5 [29]. After determining r and h, the values of r0 and h0 can be solved according to Eqs. (13) and (14), and listed in Tables 4 and 5. Fig. 10 True stress vs strain rate on logarithm scale at strains of ε=0.3 (a), ε=0.6 (b), and ε=0.9 (c) Table 4 r0 values under different temperatures and strain rates Table 5 h0 values under different temperatures and strain rates The recrystallization starts when the density of dislocations is higher than the critical dislocation density ρc. The nucleation rates were set as constants between 1×10-4 and 4×10-4 μm-3·s-1 according to the experimental results, and the grain growth rate was set as 1. CA simulation was used for an area of 1200 μm × 1200 μm with the initial grain size of 120 μm. The calculated results are shown in Fig. 11. The experimental grain sizes increase with increasing temperature and decreasing strain rate, because higher temperature and lower strain rate can offer more deformation energy and time to stimulate the growth of grains. There is a good fit between experimental and predicted data of average grain sizes, with an AARE as low as 6.3%. Therefore, the method described in this work can be used to simulate the low DRX fraction problems, especially it can be implemented in the commercial FEM software DEFORM to calculate the DRX fraction and grain size evolution during hot deformation of aluminum alloys. Fig. 11 Experimental and predicted average grain sizes of all samples 3.5 Simulation results of DRX in industrial hot rolling plate In order to further verify the validity of the modified JMAK model, industrial hot rolling of 7055 aluminum alloy thick plate was simulated with DEFORM software. A 340 mm-thick cast ingot was homogenized, then subjected to multi- pass hot rolling to a final plate of 80 mm in thickness. The true stress-strain curves, the DRX kinetics model, and other materials constants acquired from thermal simulation tests were imported into the DEFORM software. The parameters for the simulation are listed in Table 6. Table 6 Parameters for simulation of hot rolling Fig. 12 Simulation result by DEFORM-3D software (a), EBSD images (b-e) with GOS maps in insects of samples during hot rolling The distribution of XDRX on the longitudinal section of the plate is shown in Fig. 12(a). It can be found that the distribution of recrystallization area is not homogeneous, which is due to the inhomogeneous deformation of the plate during rolling. Thus, the XDRX is ranged from 0.6% to 11.8% over the whole plate. The materials in different positions of the plate, i.e., P1, P2, P3 and P4 in Fig. 12(a), were characterized by EBSD, and the results are shown in Figs. 12(b-e), respectively. The corresponding GOS maps, used for the calculation of DRX fraction, are shown in the insets as well. The plate has a typical feature of deformed and recovered microstructure. Some small DRX grains can be observed, as indicated by the red arrows. The DRX fractions are determined on the basis of the GOS map, and XDRX in the four different positions has an obvious difference, i.e., the lowest one at P1 (3.2%) and highest one at P3 (10%). A comparison between the predicted and observed XDRX is shown in Fig. 13, which basically agrees well. However, the difference between the predicted XDRX and the experimental XDRX for hot rolling is obviously higher than that for hot compression. This might be because hot compression tests were carried out on a thermal simulation machine, in which the deformation parameters were well controlled, while the deformation parameters for industrial hot rolling were not well controlled. Fig. 13 Comparison between predicted and experimental DRX fractions at different positions of hot rolling plate (Positions of P1, P2, P3 and P4 are shown in Fig. 12) 4 Conclusions (1) In 7055 aluminum alloy, DRV was easy to happen during hot deformation, therefore the DRX was very limited, lower than 12.9%. The increase of deformation temperature and decrease of strain rate could increase the fraction of DRX. (2) With the increase of temperature and the decrease of strain rate, the density of geometrically necessary dislocation (GND) gradually reduced because of DRV and/or DRX. (3) A DRX kinetics model was proposed for low proportion DRX materials. The model can be implemented in DEFORM-3D software to predict the DRX during hot compression and hot rolling very well. The AARE of the predicted DRX fraction is 13.7%. The modified JMAK-type DRX model was also used together with cellular automaton in DEFORM-3D software to predict the grain size after hot compression. The AARE of grain sizes is 6.3%. (4) The modified JMAK-type DRX model was used to simulate commercial production of 7055 aluminum alloy thick plate, and the results showed that the DRX distribution was inhomogeneous. The predicted DRX fraction agreed with experimental observation. Acknowledgments The authors are grateful for the financial supports from the National Key Research and Development Program of China (No. 2016YFB- 0300901), the National Natural Science Foundation of China (No. 51871033), the Chongqing Research Program of Basic Research and Frontier Technology, China (No. cstc2017jcyjAX0245), and the Venture & Innovation Support Program for Chongqing Overseas Returnees, China (No. cx2018002). References [1] LIAO Bin, CAO Lin-fei, WU Xiao-dong, ZOU Yan, HUANG Guang-jie, ROMETSCH P A, COUPER M J, LIU Qing. Effect of heat treatment condition on the flow behavior and recrystallization mechanisms of aluminum alloy 7055 [J]. Materials, 2019, 12(2): 311-325. [2] ZHANG Jie, LI Zhi-hui, WEN Kai, HUANG Shu-hui, LI Xi-wu, YAN Hong-wei, YAN Li-zhen, LIU Hong-wei, ZHANG Yong-an, XIONG Bai-qing. Simulation of dynamic recrystallization for an Al-Zn-Mg-Cu alloy using cellular automaton [J]. Progress in Natural Science: Materials International, 2019, 29(4): 477-484 . [3] AZARBARMAS M, MIRJAVADI S, GHASEMI A, HAMOUDA A. A combined method to model dynamic recrystallization based on cellular automaton and a phenomenological (CAP) approach [J]. Metals, 2018, 8(11): 923-937. [4] HUANG K, LOGER E. A review of dynamic recrystallization phenomena in metallic materials [J]. Materials & Design, 2016, 111: 548-574. [5] LIN Y C, WU X Y, CHEN X M, CHEN J, WEN D X, ZHANG J L, LI L T. EBSD study of a hot deformed nickel-based superalloy [J]. Journal of Alloys and Compounds, 2015, 640: 101-113. [6] ESTRIN Y, MECKING H. A unified phenomenological description of work hardening and creep based on one-parameter models [J]. Acta Metallurgica, 1984, 32(1): 57-70. [7] AVRAMI M. Kinetics of phase change. I: General theory [J]. Journal of Chemical Physics, 1939, 7(12): 1103-1112. [8] SELLARS C M, WHITEMAN J A. Recrystallization and grain growth in hot rolling [J]. Metal Science, 1979, 13(3-4): 187-194. [9] MEDINA S F, HERNANDEZ C A. Modelling of the dynamic recrystallization of austenite in low alloy and microalloyed steels [J]. Acta Materialia, 1996, 44(1): 165-171. [10] POLIAK E I, JONAS J J. A one-parameter approach to determining the critical conditions for the initiation of dynamic recrystallization [J]. Acta Materialia, 1996, 44(1): 127-136. [11] SAITO Y. Modeling of microstructural evolution in thermomechanical processing of structural steels [J]. Materials Science and Engineering A, 1997, 223: 134-145. [12] HADADZADEH A, MOKDAD F, WELLS M A, CHEN D L. Modeling dynamic recrystallization during hot deformation of a cast-homogenized Mg-Zn-Zr alloy [J]. Materials Science and Engineering A, 2018, 720(21): 180-188. [13] WANG Sheng-long, ZHANG Ming-xian, WU Huan-chun, YANG Bin. Study on the dynamic recrystallization model and mechanism of nuclear grade 316LN austenitic stainless steel [J]. Materials Characterization, 2016, 118: 92-101. [14] XU Yan, CHEN Chen, ZHANG Xu-xing, DAI Hao-hao, JIA Jian-bo, BAI Zhen-hua. Dynamic recrystallization kinetics and microstructure evolution of an AZ91D magnesium alloy during hot compression [J]. Materials Characterization, 2018, 145: 39-52. [15] CHEN Liang, SUN Wei-yan, LIN Jun, ZHAO Guo-qun, WANG Guang-chun. Modelling of constitutive relationship, dynamic recrystallization and grain size of 40Cr steel during hot deformation process [J]. Results in Physics, 2019, 12: 784-792. [16] MIRZAEE M, KESHMIRI H, EBRAHIMI G R, MOMENI A. Dynamic recrystallization and precipitation in low carbon low alloy steel 26NiCrMoV 14-5 [J]. Materials Science and Engineering A, 2012, 551: 25-31. [17] ZANG Q H, YU H S, LEE Y S, KIM M S, KIM H W. Hot deformation behavior and microstructure evolution of annealed Al-7.9Zn-2.7Mg-2.0Cu (wt.%) alloy [J]. Journal of Alloys and Compounds, 2018, 763: 25-33. [18] LI Dong-feng, ZHANG Duan-zheng, LIU Sheng-dan, SHAN Zhao-jun, ZHANG Xin-ming, WANG Qin, HAN Su-qi. Dynamic recrystallization behavior of 7085 aluminum alloy during hot deformation [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(6): 1491-1497. [19] HIELSCHER R, BARTEL F, BRITTON T B. Gazing at crystal balls: Electron backscatter diffraction pattern analysis and cross correlation on the sphere [J]. Ultramicroscopy, 2019, 207: 112836. [20] DAI Qing-song, DENG Yun-lai, TANG Jian-guo, WANG Yu. Deformation characteristics and strain-compensated constitutive equation for AA5083 aluminum alloy under hot compression [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(11): 2252-2261. [21] KAPOOR R, SINGH J B, CHAKRAVARTTY J K. High strain rate behavior of ultrafine-grained Al-1.5Mg [J]. Materials Science and Engineering A, 2008, 496: 308-315. [22] ZHAO Jiu-hui, DENG Yun-lai, TAN Jia, ZHANG Jin. Effect of strain rate on the recrystallization mechanism during isothermal compression in 7050 aluminum alloy [J]. Materials Science and Engineering A, 2018, 734: 120-128. [23] NAYAN N, MURTY S V S N, CHHANGANI S, PRAKASH A, PRASAD M J N V, SAMAJDAR I. Effect of temperature and strain rate on hot deformation behavior and microstructure of Al-Cu-Li alloy [J]. Journal of Alloys and Compounds, 2017, 723: 548-558. [24] TANG Xue-feng, WANG Bao-yu, JI Hong-chao, FU Xiao-bin, XIAO Wen-chao. Behavior and modeling of microstructure evolution during metadynamic recrystallization of a Ni-based superalloy [J]. Materials Science and Engineering A, 2016, 675: 192-203. [25] BACHMANN F, HIELSCHER R, SCHAEBEN H. Texture analysis with MTEX-free and open source software toolbox [J]. Solid State Phenomena, 2010, 160: 63-68. [26] ROBERTS W, AHLBLOM B. A nucleation criterion for dynamic recrystallization during hot working [J]. Acta Metallurgica, 1978, 26(5): 801-813. [27] ZHANG Yan-qiu, JIANG Shu-yong, LIANG Yu-long, HU Li. Simulation of dynamic recrystallization of NiTi shape memory alloy during hot compression deformation based on cellular automaton [J]. Computational Materials Science, 2013, 71: 124-134. [28] ZHANG Tao, LU Shi-hong, WU Yun-xin, GONG Hai. Optimization of deformation parameters of dynamic recrystallization for 7055 aluminum alloy by cellular automaton [J]. Transactions of Nonferrous Metals Society of China, 2017, 27(6): 1327-1337. [29] LI Jun-chao, XIE Zhi-yuan, LI Song-pu, ZANG Yan-yan. Modeling on dynamic recrystallization of aluminium alloy 7050 during hot compression based on cellular automaton [J]. Journal of Central South University, 2016, 23(3): 497-507. [30] TAN Kai, LI Jian, GUAN Zhi-jun, YANG Jia-bing, SHU Jian-xun. The identification of dynamic recrystallization and constitutive modeling during hot deformation of Ti55511 titanium alloy [J]. Materials & Design, 2015, 84(5): 204-211. [31] FIELD D, BRADFORD L, NOWELL M, LILLO T. The role of annealing twins during recrystallization of Cu [J]. Acta Materialia, 2007, 55(12): 4233-4241. [32] CAO Yu, DI Hong-shuang, ZHANG Jing-qi, ZHANG Jie-cen, MA Tian-jun, MISRA R D K. An electron backscattered diffraction study on the dynamic recrystallization behavior of a nickel-chromium alloy (800H) during hot deformation [J]. Materials Science and Engineering A, 2013, 585(15): 71-85. [33] YIN Xiang-qian, PARK C H, LI Yan-feng, YE Wen-jun, ZUO Yu-ting, LEE S W, YEOM J T, MI Xu-jun. Mechanism of continuous dynamic recrystallization in a 50Ti-47Ni-3Fe shape memory alloy during hot compressive deformation [J]. Journal of Alloys and Compounds, 2017, 693(5): 426-431. [34] BARRETT C D, IMANDOUST A, OPPEDAL A L, INAL K, TSCHOPP M A, EL KADIRI H. Effect of grain boundaries on texture formation during dynamic recrystallization of magnesium alloys [J]. Acta Materialia, 2017, 128(15): 270-283. [35] LAASRAOUI A, JONAS J J. Prediction of steel flow stresses at high temperatures and strain rates [J]. Acta Metallurgica, Metallurgical Transactions A, 1991, 22: 1545-1558. [36] LI Shi-kang, LI Luo-xing, HE Hong, LIU Zhi-wen, ZHANG Long. Influence of dynamic recrystallization on microstructure and mechanical properties of welding zone in Al-Mg-Si aluminum profile during porthole die extrusion [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(9): 1803-1815. [37] QUAN Guo-zheng, ZHANG Kai-kai, AN Chao, QIU Hui-min, XIA Yu-feng. Analysis of dynamic recrystallization behaviors in resistance heating compressions of heat-resistant alloy by multi-field and multi-scale coupling method [J]. Computational Materials Science, 2018, 149(15): 73-83. [38] MONTHEILLET F, LURDOS O, DAMAMME G. A grain scale approach for modeling steady-state discontinuous dynamic recrystallization [J]. Acta Materialia, 2009, 57(5): 1602-1612. [39] LI Peng-wei, LI Hui-zhong, HUANG Lan, LIANG Xiao-peng, ZHU Ze-xiao. Characterization of hot deformation behavior of AA2014 forging aluminum alloy using processing [J]. Transactions of Nonferrous Metals Society of China, 2017, 27(8): 1677-1688. [40] CAO Zhuo-han, SUN Yu, ZHOU Chen, WAN Zhi-peng, YANG Wen-hua, REN Li-li, HU Lian-xi. Cellular automaton simulation of dynamic recrystallization behavior in V-10Cr-5Ti alloy under hot deformation conditions [J]. Transactions of Nonferrous Metals Society of China, 2019, 29(1): 98-111. 李佳宸1,吴晓东1,廖 斌2,蔺晓敏1,曹玲飞1,3 1. 重庆大学 材料科学与工程学院 教育部轻合金材料国际合作联合实验室,重庆 400044; 2. 南南铝业股份有限公司,南宁 530031; 3. 重庆大学 沈阳材料科学国家研究中心,重庆 400044 摘 要:研究7055铝合金在温度为390~470 °C 和应变速率为0.01~1 s-1条件下热变形和动态再结晶行为。电子背散射衍射(EBSD)表征结果表明,7055铝合金在热变形下动态再结晶含量较低,动态再结晶含量为1%~13%。为了模拟低比例动态再结晶问题,对JMAK动态再结晶模型进行修正。应用修正的模型,结合商业有限元软件DEFORM-3D,对7055铝合金的热压缩过程进行数值模拟,模拟得到的动态再结晶比例和晶粒尺寸的平均绝对相对误差(AARE)分别为13.7%和6.3%,与实验结果吻合良好。为了进一步证实该模型的有效性,采用该方法对7055铝合金工业化热轧过程进行模拟,模拟结果表明热轧板的动态再结晶分布不均匀,与实验观察结果一致。 关键词:动态再结晶;JMAK模型;DEFORM-3D;7055铝合金;热压缩 (Edited by Wei-ping CHEN) Corresponding author: Xiao-dong WU, Tel: +86-18581029651, E-mail: xiaodongwu@cqu.edu.cn; Ling-fei CAO, Tel: +86-13996310689, E-mail: caolingfei@cqu.edu.cn DOI: 10.1016/S1003-6326(21)65625-X 1003-6326/ (2)
(2)
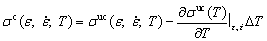 (3)
(3) is the strain rate, T is the temperature, and ΔT is the difference between the setting temperature and true temperature. An example of the flow stress-strain curves after temperature correction is shown in Fig. 2(e), and an obvious change in flow stress after correction can be observed.
is the strain rate, T is the temperature, and ΔT is the difference between the setting temperature and true temperature. An example of the flow stress-strain curves after temperature correction is shown in Fig. 2(e), and an obvious change in flow stress after correction can be observed.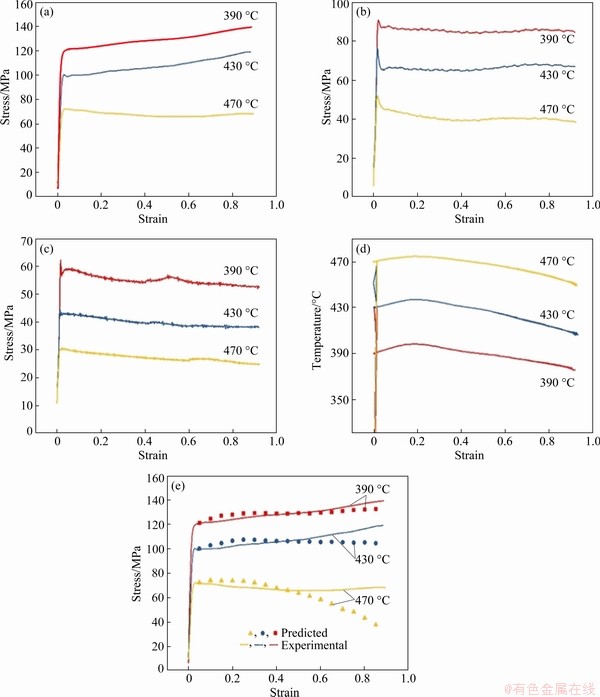

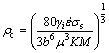 (4)
(4)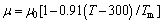 (5)
(5)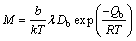 (6)
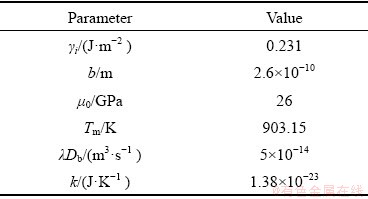
(6)
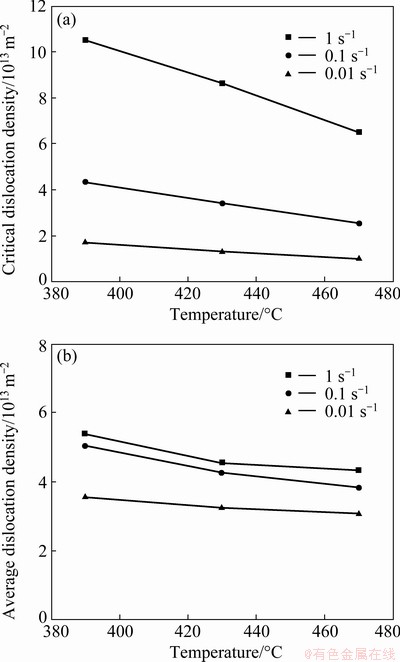
 (7)
(7)
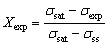 (8)
(8)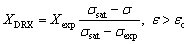 (9)
(9)
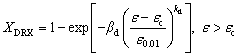 (10)
(10)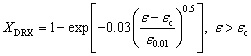 (11)
(11)
 (12)
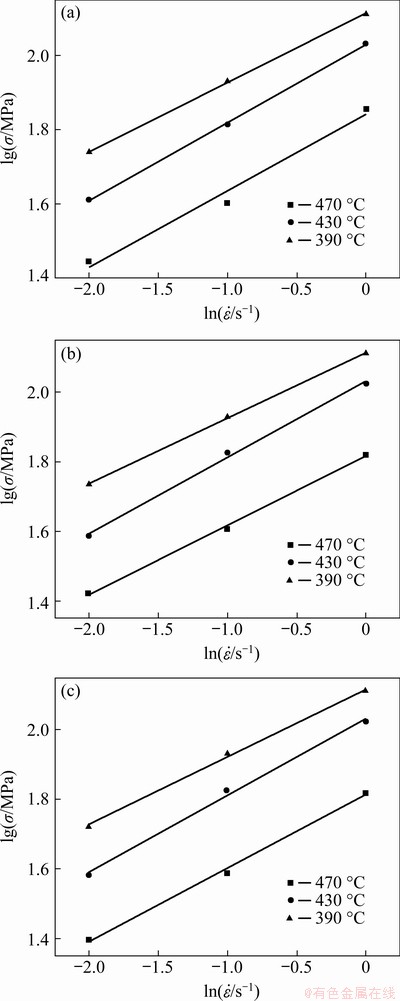
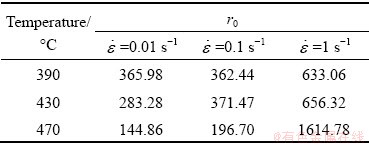
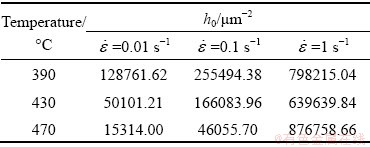
(12)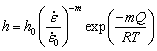 (13)
(13)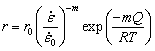 (14)
(14)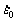 is the strain rate calibration constant and is taken as 1 in the commercial FEM DEFORM-3D software, h0 and r0 are the initial hardening parameter and the initial recovery parameter, respectively, Q is the activation energy from the modified JMAK-type equation, and m is the strain rate sensitivity [39,40], which is related to the material hardening tendency with the increase of strain rate. The calculation formula of m could be described as
is the strain rate calibration constant and is taken as 1 in the commercial FEM DEFORM-3D software, h0 and r0 are the initial hardening parameter and the initial recovery parameter, respectively, Q is the activation energy from the modified JMAK-type equation, and m is the strain rate sensitivity [39,40], which is related to the material hardening tendency with the increase of strain rate. The calculation formula of m could be described as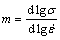 (15)
(15)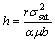 (16)
(16)



7055铝合金中低比例动态再结晶的模拟
 2021 The Nonferrous Metals Society of China. Published by Elsevier Ltd & Science Press
2021 The Nonferrous Metals Society of China. Published by Elsevier Ltd & Science Press

