DOI: 10.11817/j.issn.1672-7207.2018.07.028
基于反应谱法的低重心斜拉桥判定简化计算
张文学,陈盈,寇文琦,汪振
(北京工业大学 建筑工程学院,北京,100124)
摘要:为便于斜拉桥抗震方案比选,建立全漂浮体系斜拉桥反向双质点简化分析模型和纵向铰接体系斜拉桥双质点简化分析模型,并推导2种体系斜拉桥纵向一阶自振周期的简化计算公式。根据反应谱计算理论得到全漂浮体系和纵向铰接体系斜拉桥塔底弯矩的简化计算公式,提出简化的低重心斜拉桥判定公式,并与10座已建斜拉桥的有限元计算结果进行对比验证,弯矩吻合良好。研究结果表明:2种不同体系斜拉桥纵向一阶自振周期简化计算公式均具有较高的计算精度,基于反应谱法提出的低重心斜拉桥简化判定公式具有较高的可靠性,可为斜拉桥初步设计时抗震方案必选提供参考。
关键词:斜拉桥;漂浮体系;纵向铰接体系;双质点模型;低重心
中图分类号:U442.5 文献标志码:A 文章编号:1672-7207(2018)07-1793-06
Simplified criterion for low gravity center cable-stayed bridge based on response spectrum
ZHANG Wenxue, CHEN Ying, KOU Wenqi, WANG Zhen
(College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China)
Abstract: In order to make scheme comparison of cable-stayed bridges convenient, the reverse double-mass model for full floating cable-stayed bridges and the double-mass model for fixed hinge cable-stayed bridges were developed, and based on the simplified models, the formulas were derived. Then, on the basis of the double-mass models and the response spectrum, the simplified calculation of the bottom bending moment and simplified criterion of low gravity center cable-stayed bridges were put forward. Finally, the proposed models and simplified calculation were evaluated by the tests on ten built-up bridges and the simplified calculation results were matched well with those analyzed by finite element method. The results show that the two simplified models have higher accuracy and the criterion of low gravity center cable-stayed bridge is reliable, they can be adopted in preliminary design and scheme comparison of cable-stayed bridges.
Key worlds: cable-stayed bridges; full floating system; fixed hinge system; double-mass models; low gravity center
斜拉桥是一种具有很强竞争力的大跨度桥型,建设广泛[1-2],其结构体系直接关系到抗震性能,根据具体场地类型和结构特性选择合理的结构体系对斜拉桥的抗震性能至关重要。目前研究认为漂浮体系斜拉桥的纵向刚度较小,为长周期结构[3],在地震荷载作用下主塔控制截面内力响应较小;而纵向铰接体系斜拉桥的纵向刚度较大,可以有效地控制地震荷载作用下关键点的纵向位移响应,但主塔控制截面的内力响应比较大[4]。相比而言,全漂浮体系可以有效降低斜拉桥主塔控制截面的地震内力需求[5-6]。但以上结论是基于常规斜拉桥得出的,并未考虑重心高度对不同体系斜拉桥地震响应特性的影响,而目前关于低重心斜拉桥地震响应特性的研究还较少,还没有低重心斜拉桥简化判定方法。结构动力分析是桥梁动力响应、地震分析的基础[7-8],提出一套精度较高的斜拉桥自振周期计算公式是斜拉桥地震响应简化计算的基础[9-11]。虽然已有学者提出全漂浮体系斜拉桥自振周期简化计算方法[12-14],但其计算精度相对较低。目前关于纵向铰接体系斜拉桥纵向自振周期简化计算的研究还很少,为此,本文作者分别建立漂浮体系和纵向铰接体系斜拉桥纵向自振周期简化计算的双质点模型,推导其自振周期计算公式。在此基础上,采用规范反应谱得到2种不同体系斜拉桥塔底弯矩简化计算公式,根据低重心斜拉桥判定准则[15],建立低重心斜拉桥判定公式,并通过10座已建斜拉桥的有限元分析结果对其可靠性进行验证。
1 斜拉桥自振周期简化计算
1.1 全漂浮体系斜拉桥
将塔底简化为固结,基于斜拉桥水平地震惯性力传递路径可将全漂浮体系斜拉桥简化为如图1所示的反向双质点模型。图1中,主塔的等效质量mt堆聚到塔顶,主梁质量mb堆聚在梁体重心位置,并可绕着塔顶摆动;utt和ub分别为塔顶纵向位移和主梁纵向位移;lc为拉索等效摆长,近似取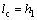 ;
; 为纵飘振动时主梁摆过的角度,由此可得主梁等效摆动刚度Kbf [13]。
为纵飘振动时主梁摆过的角度,由此可得主梁等效摆动刚度Kbf [13]。
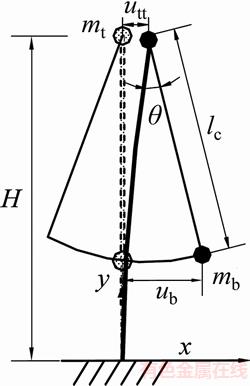
图1 反向双质点简化模型
Fig. 1 Simplified model of reverse double-mass
假设该双自由度体系的自由振动是简谐振动,忽略拉索的弹性变形和结构的阻尼效应,采用刚度法,基于结构动力学方法解得简化结构的频率为
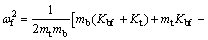
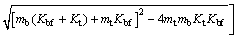 (1)
(1)
式中:Kt为塔顶处的抗推刚度。
由此可得全漂浮体系斜拉桥的纵向一阶自振周期Tf为
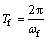 (2)
(2)
1.2 纵向铰接体系斜拉桥
对应纵向铰接体系斜拉桥,将上塔柱等效质量mp堆聚在上塔柱重心处,主梁质量和下塔柱等效质量之和md堆聚在下塔柱重心处,则纵向铰接体系斜拉桥可
简化成双质点模型,如图2所示。其中,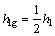 ;
;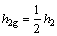 ;up和ud分别为mp和md的纵向位移。
;up和ud分别为mp和md的纵向位移。

图2 双质点简化模型
Fig. 2 Simplified model of double-mass
假设该双自由度体系的自由振动是简谐振动,忽略拉索的弹性变形和结构的阻尼效应,采用柔度法,基于结构动力学方法可知简化结构的频率为
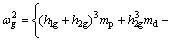

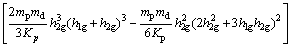 (3)
(3)
式中:Kp为主塔的纵向弯曲刚度。
因此,纵向铰接体系斜拉桥的纵向一阶自振周期Tg为
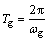 (4)
(4)
1.3 自振周期简化公式验证
为验证基于双质点模型的斜拉桥自振周期简化计算公式的可靠性,选取了10座典型斜拉桥进行对比,其基本参数见表1。其中,济南三桥、松花江大桥、松原大桥、南叶公路桥、海河大桥为单塔斜拉桥;飞云江大桥、金塘大桥、七都大桥、台州湾主桥、苏通大桥为双塔斜拉桥。采用结构分析有限元软件SAP2000分别建立这10座斜拉桥全漂浮体系和纵向铰接体系有限元模型,进行模态分析得纵向一阶自振周期,并将其与利用式(2)和文献[12]计算得到的全漂浮体系斜拉桥简化一阶纵飘振动周期以及利用式(4)计算得到的纵向铰接体系斜拉桥纵向一阶自振周期进行对比,如表2所示。从表2可知:
1) 采用本文提出的反向双质点模型计算得10座全漂浮体系斜拉桥纵向一阶自振周期与有限元分析计算结果的最大相对计算误差为-3.40%,平均相对误差均仅为-0.14%,而采用文献[12]中的单质点模型简化计算公式得到结果相对误差较大,最大相对计算误差为26.42%;双质点简化模型计算所得10座纵向铰接体系斜拉桥纵向一阶自振周期与有限元分析结果的最大相对计算误差为-5.22%,平均相对误差仅为0.05%,说明本文基于双质点简化模型推导的漂浮体系斜拉桥和纵向铰接体系斜拉桥纵向一阶周期简化计算公式具有较高的精度。
表1 算例斜拉桥主要计算参数
Table 1 Structure parameters of cable-stayed bridges in calculation
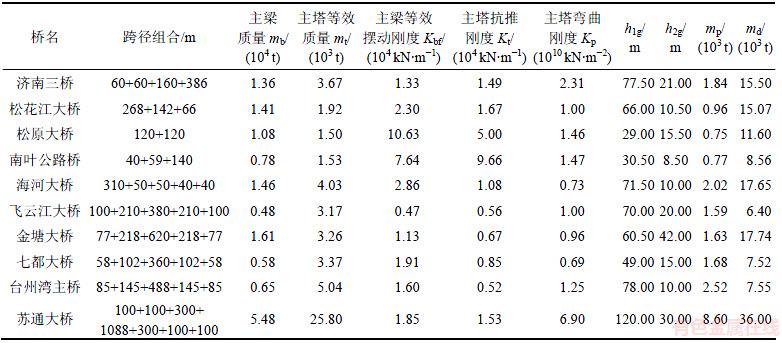
表2 周期计算结果对比
Table 2 Comparison of estimated period

2) 基于双质点简化模型求得的全漂浮体系斜拉桥和纵向铰接体系斜拉桥纵向一阶自振周期相对误差的标准差分别为2.05%和3.61%,说明本文提出的斜拉桥纵向一阶自振周期简化计算方法具有较强的稳 定性。
2 低重心斜拉桥判定
2.1 斜拉桥塔底弯矩简化计算
1) 漂浮体系斜拉桥纵向一阶振型的贡献率一般在90%以上,由漂浮体系斜拉桥纵向自振周期简化计算公式,结合规范反应谱得漂浮体系斜拉桥塔底弯矩响应简化计算公式如下:
 (5)
(5)
式中: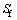 为漂浮体系斜拉桥纵向一阶自振周期对应的反应谱加速度。
为漂浮体系斜拉桥纵向一阶自振周期对应的反应谱加速度。
2) 根据纵向铰接体系斜拉桥纵向自振周期简化计算公式,在不考虑振型贡献率的情况下,纵向铰接体系斜拉桥塔底弯矩响应简化计算为
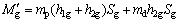 (6)
(6)
由于纵向铰接体系斜拉桥纵向一阶振型的贡献率约为30%[12],为此需对式(6)中反应谱加速度Sg进行修正,引入修正系数后纵向铰接体系斜拉桥顺桥向塔底弯矩计算式为
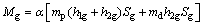 (7)
(7)
式中: 为修正系数;Sg为纵向铰接体系斜拉桥纵向一阶自振周期对应的反应谱加速度。
为修正系数;Sg为纵向铰接体系斜拉桥纵向一阶自振周期对应的反应谱加速度。
为确定修正系数 ,以济南三桥(单塔斜拉桥)和七都大桥(双塔斜拉桥)为原型,通过改变原模型的下塔柱高度h2来得到不同重心高度的计算模型,以下塔柱高h2g与总塔柱高H之比
,以济南三桥(单塔斜拉桥)和七都大桥(双塔斜拉桥)为原型,通过改变原模型的下塔柱高度h2来得到不同重心高度的计算模型,以下塔柱高h2g与总塔柱高H之比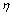 为变量。分别研究4种不同类场地规范反应谱下纵向铰接体系单塔斜拉桥和双塔斜拉桥桥纵向塔底弯矩简化计算公式修正系数
为变量。分别研究4种不同类场地规范反应谱下纵向铰接体系单塔斜拉桥和双塔斜拉桥桥纵向塔底弯矩简化计算公式修正系数 的取值情况。分析时取
的取值情况。分析时取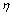 =1/10~5/10,将采用式(6)计算得纵向铰接体系斜拉桥塔底弯矩与有限元反应谱分析结果进行对比,对比结果见表3,由此可知修正系数
=1/10~5/10,将采用式(6)计算得纵向铰接体系斜拉桥塔底弯矩与有限元反应谱分析结果进行对比,对比结果见表3,由此可知修正系数 受场地类型的影响很小,可以忽略,可简单取值如下:
受场地类型的影响很小,可以忽略,可简单取值如下:
1) 对于单塔斜拉桥, 。
。
2) 对于双塔斜拉桥, 。
。
2.2 低重心斜拉桥判定
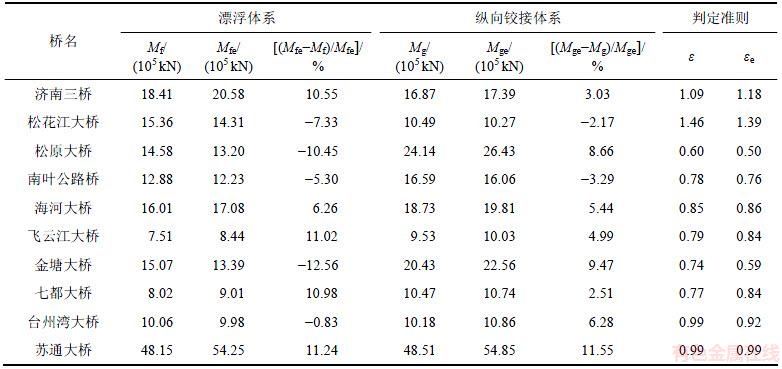
在某类场地地震荷载作用下,按漂浮体系计算出的塔底顺桥向弯矩Mfi与按纵向铰接体系计算出的塔底顺桥向弯矩Mgi的比值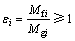 的斜拉桥即称为该类场地地震作用下的低重心斜拉桥。
的斜拉桥即称为该类场地地震作用下的低重心斜拉桥。
根据塔底弯矩简化计算公式(5)和(7)结合已有的低重心斜拉桥判定准则,得低重心斜拉桥判定公式为
 (8)
(8)
当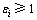 时,为低重心斜拉桥;当
时,为低重心斜拉桥;当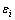 <1时,为常规斜拉桥。
<1时,为常规斜拉桥。
2.3 低重心斜拉桥判定公式验证
为验证塔底弯矩简化计算公式及简化的低重心斜拉桥判定公式的可靠性。由2.1节可知场地类型对塔底弯矩及判定公式的变化趋势影响较小,故采用与2.1节相同的反应谱分析方法仅取III类场地反应谱分析表2中所列10座斜拉桥。采用式(5)计算得Mf、采用式(7)计算得Mg与有限元计算结果进行对比,采用式(8)计算得ε与有限元计算得εe进行对比,结果见表4,由此可知:
1) 根据漂浮体系斜拉桥塔底弯矩简化计算公式(5)所得10座全漂浮体系斜拉桥塔底弯矩与有限元计算结果之间的最大相对误差为-12.56%,最小相对误差仅为-0.83%,平均相对误差为1.36%,说明本文提出全漂浮体系斜拉桥塔底弯矩简化计算公式具有较高的计算精度。
2) 根据纵向铰接体系斜拉桥塔底弯矩简化计算公式(7)所得10座纵向铰接体系斜拉桥塔底弯矩与有限元计算结果之间的最大相对误差为11.55%,最小相对计算误差仅为-2.17%,平均相对误差为4.65%,说明本文提出纵向铰接体系斜拉桥塔底弯矩简化计算公式是合理的。
3) 全漂浮体系斜拉桥和纵向铰接体系斜拉桥塔底弯矩简化计算结果相对误差的标准差分别为9.22%和4.55%,说明该简化计算方法具有较强的稳定性。
4) 低重心斜拉桥判定公式(8)的判定结果与有限元所得结论相同,说明本文提出的低重心斜拉桥判定公式具有较好的可靠性,可为斜拉桥初步设计阶段合理结构体系选择提供参考。
表3 修正系数计算结果
Table 3 Computation of correction coefficient

表4 实例对比
Table 4 Comparison of instances
3 结论
1) 基于全漂浮体系斜拉桥反向双质点简化模型和纵向铰接体系斜拉桥双质点简化模型推导的2种体系斜拉桥纵向一阶自振周期计算公式具有较高的计算精度和较强的稳定性。
2) 利用斜拉桥纵向自振周期简化计算公式结合反应谱分析方法,建立的低重心斜拉桥判定公式是可行的,可为斜拉桥的初步设计和方案选择提供参考。
参考文献:
[1] 谢文, 孙利民. 采用耗能辅助墩的超大跨斜拉桥顺桥向地震损伤控制[J]. 中南大学学报(自然科学版), 2013, 44(11): 4672-4681.
XIE Wen, SUN Limin. Seismic damage control of long span cable-stayed bridges by supporting piers with energy dissipating in longitudinal direction[J]. Journal of Central South University (Science and Technology), 2013, 44 (11): 4672-4681.
[2] ASTIZ M A., CAMARA A. Analysis and control of cable-stayed bridges subject to seismic action[J]. Structural Engineering International, 2014, 24(1): 27-36.
[3] REN Weixin, PENG Xuelin, LIN Youqin. Experimental and analytical studies on dynamic characteristics of a large span cable-stayed bridge[J]. Engineering Structures, 2005, 27(4): 535-548.
[4] 张文学, 李建中, 李怀峰. 低重心斜拉桥地震响应特性研究[J]. 桥梁建设, 2007(5): 21-23, 41.
ZHANG Wenxue, LI Jianzhong, LI Huaifeng. Study of seismic response characteristics of low gravity center cable-stayed bridge[J]. Bridge Construction, 2007(5): 21-23, 41.
[5] 李永乐, 乔倩妃, 陈克坚, 等. 大跨度铁路斜拉桥车致纵向振动及塔梁连接研究[J]. 桥梁建设, 2014, 44(2): 12-19.
LI Yongle, QIAO Qianfei, CHEN kejian, et al. Study of vehicle-induced longitudinal vibration and connection between pylon and girder of long span railway cable-stayed bridges[J]. Bridge Construction, 2014, 44(2): 12-19.
[6] 燕斌, 杜修力, 韩强, 等. 减隔震混合装置在独塔斜拉桥抗震设计中的应用[J]. 桥梁建设, 2014, 44(6): 101-106.
YAN bin, DU Xiuli, HAN Qiang, et al. Application of hybrid seismic mitigation and isolation device to seismic design of single-pylon cable-stayed bridge[J]. Bridge Construction, 2014, 44(6): 101-106.
[7] 柳成荫, 何显银, 张海江. 基于无线传感器网络的斜拉桥模型动力特性分析[J]. 中南大学学报(自然科学版). 2014, 45(1): 208-213.
LIU Chengyin, HE Xianyin, ZHANG Haijiang. Analysis of dynamic characteristics for a cable-stayed bridge model using wireless sensor network[J]. Journal of Central South University (Science and Technology), 2014, 45(1): 208-213.
[8] 范立础, 胡世德, 叶爱君. 大跨度桥梁抗震设计[M]. 北京: 人民交通出版社, 2001: 19-22.
FAN Lichu, HU Shide, YE Aijun. Seismic design of long-span bridge[M]. Beijing: China Communication Press, 2001: 19-22.
[9] AU F T K, CHENG Y S, CHEUNG Y K. On the determination of natural frequencies and mode shapes of cable-stayed bridges[J]. Applied Mathematical Modeling, 2011, 25(12): 1099-1115.
[10] STRAUPE V, PAEGLITIS A. Analysis of geometrical and mechanical properties of cable-stayed bridge[J]. Procedia Engineering, 2013, 57(1): 1086-1093.
[11] CAMARA A. Mode estimation for modern cable-stayed bridges considering the tower flexibility[J]. Journal of Bridge Engineering, 2014, 19(6): 213-226.
[12] 李国豪. 桥梁结构稳定与振动[M]. 北京: 中国铁道出版社, 1996: 390-391.
LI Guohao. Stability and vibration of bridge structured[M]. Beijing: China Railway Publishing House, 1996: 390-391.
[13] 袁万成, 闫冬. 斜拉桥纵飘频率简化计算方法[J]. 同济大学学报(自然科学版), 2005, 33(11): 1423-1427.
YUAN Wancheng, YAN Dong. Simplified calculational method of floating frequency for cable-stayed bridges[J]. Journal of Tongji University (Natural Science), 2005, 33(11): 1423-1427.
[14] 张文学, 寇文琦, 陈盈, 等. 基于能量法的斜拉桥纵向1阶自振周期简化计算[J]. 中国公路学报, 2017, 30(7): 50-57.
ZHANG Wenxue, KOU Wenqi, CHEN Ying, et al. Simplified calculation of first-order longitudinal natural vibration period of cable-stayed bridges based on energy method[J]. China Journal of Highway and Transport, 2017, 30(7): 50-57.
[15] 张文学, 王景景, 陈士通. 重心高度对不同体系斜拉桥地震响应特性影响研究[J]. 公路, 2015(1): 72-76.
ZHANG Wenxue, WANG Jingjing, CHEN Shitong. Study of seismic response characteristics of gravity center’s height to different structure system cable-stayed bridge[J]. Highway, 2015(1): 72-76.
(编辑 杨幼平)
收稿日期:2017-07-03;修回日期:2017-09-28
基金项目(Foundation item):国家自然科学基金面上资助项目(51378034,E080505);北京市自然科学基金面上资助项目(8122007) (Projects(51378034, E080505) supported by the National Natural Science Foundation of China; Project(8122007) supported by the Beijing Science Foundation)
通信作者:陈盈,博士,副教授,从事结构抗震研究;E-mail: chenying@bjut.edu.cn