文章编号:1004-0609(2013)11-3202-09
过饱和液相内析出-长大行为的蒙特卡罗模拟
张晓泳1, 2,刘邵生3,鲍寅祥2,李小斌1,周科朝2
(1. 中南大学 冶金与环境学院,长沙 410083;
2. 中南大学 粉末冶金国家重点实验室,长沙 410083;
3. 世泰科化工贸易(上海)有限公司,上海 200030)
摘 要:采用蒙特卡罗方法模拟过饱和液相体系内的析出-长大行为,其中针对溶质扩散、溶质析出以及颗粒溶解等微观过程分别制定模拟规则,并在分析模拟数据时引入临界晶核,考虑液相析出浓度与临界形核尺寸之间的关联性。模拟结果表明,随着模拟时间延长,液相浓度和过饱和度均呈现出急剧下降、缓慢下降、最后趋于平衡稳定的变化趋势。模拟温度越低,则平衡浓度越低,达到平衡浓度所需时间越长,并且在图形模拟结果中形成更多、更小的溶质格点聚集析出微区。在延长模拟时间的过程中,会发生Ostwald熟化长大,并且平均析出颗粒半径呈抛物线增加,提高模拟温度则会引起更快的析出长大行为,各种模拟温度下得到的颗粒长大指数在0.320~0.332之间,不随模拟温度变化发生较大波动。上述模拟结果与NiFe2O4-KCl熔盐体系和SrMoO4过饱和溶液体系在降低温度和延长保温时间过程中的实验现象以及在扩散过程控制下的Ostwald熟化长大理论较为吻合。
关键词:过饱和液相;蒙特卡罗方法;模拟;析出;长大
中图分类号:TG111;TP 391.7 文献标志码:A
Monte Carlo simulation for precipitation and growth behaviors in supersaturated liquid
ZHANG Xiao-yong1, 2, LIU Shao-sheng3, BAO Yin-xiang2, LI Xiao-bin1, ZHOU Ke-chao2
(1. School of Metallurgy and Environment, Central South University, Changsha 410083, China;
2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China;
3. H.C. Starck Trading(Shanghai) Co., Ltd., Shanghai 200030, China)
Abstract: The precipitation-growth progress in the supersaturated liquid was simulated by the Monte Carlo method. The simulation rules were established to simulate the micro-processes of solute diffusion, solute precipitation, and particle dissolution. The critical nucleus and the relationship between the critical nucleus size and liquid concentration were considered for analyzing the simulation data. The results show that during prolonging the simulation time, the liquid concentration and supersaturation ratio show rapid decrease, and slow decrease up to equilibrium sequentially. With decreasing simulation temperature, the equilibrium concentration decreases and the time to attain equilibrium becomes longer, and the solute lattices precipitate to form more smaller aggregations in the graphic results. Ostwald ripening growth occurs by prolonging the simulation time, in which the average precipitated particle radius increases parabolically. This growth is promoted by raising the simulation temperature. The particle growth exponents of 0.320-0.332 have only a tiny fluctuation when changing the simulation temperature. The simulation results are consistent with the temperature-decreasing and time-prolonging experiments of NiFe2O4-KCl molten salt system and SrMoO4 supersaturated solution, and the Ostwald ripening theory based on the diffusion-controlled kinetics.
Key words: supersaturated liquid; Monte Carlo method; simulation; precipitation; growth
当液相体系中存在一定过饱和度时,会发生形核析出-长大的现象。在析出过程中,溶质通过能量起伏和结构起伏聚集在一起,构成短程有序的基元团(即晶胚);一部分晶胚继续长大、直至超过临界形核尺寸后,析出固相颗粒,液相浓度随之下降,并逐渐由不稳定的过饱和状态转变为稳定的平衡浓度状态,形核驱动力为过饱和度[1]。液相体系内发生的析出-长大过程是材料科学中的基本现象之一,化学共沉淀[2]、溶胶-凝胶[3]、熔盐合成[4]等诸多涉及液相的材料合成与制备方法与该现象密切相关,并且会对合成产物的数量、结晶尺寸与形貌等产生重要作用,因此,关于此方面的研究在材料学领域受到广泛关注。
目前,针对液相体系析出-长大的实验研究主要采用激光共聚焦显微观察[5]、相衬-微分干涉显微观 察[6]、迈克尔逊干涉[7]、双脉冲[8]等直接观察的方式,通过对形成核心进行计时计数,获得形核孕育期、形核数量等结果。然而,由于形核析出发生的尺度范围极小(纳观到微观尺度)、时间极短(数十微秒)[9],因此,采用实验观察的研究手段,在精确获得实验结果(诸如液相浓度变化、形核率、临界形核尺寸等)、实时探测动态行为等方面存在较大局限性,尤其在研究不透明溶液或者高温液相时,上述问题尤显突出。
随着计算材料学和计算机技术的迅速发展,采用计算模拟的方式研究液相析出-长大行为日益受到关注。这类研究手段主要通过构建对象模型、制定驱动规则、存储并分析模拟数据等一系列环节,实现析出-长大微观过程的模拟,进而预测相关规律及动力学行为。目前,用于模拟液相析出-长大行为的方法主要有分子动力学[10]、相场[11]和蒙特卡罗等,其中蒙特卡罗方法(Monte Carlo method,MC)的模拟程序设计相对简单,模拟速度相对较快,并且可以利用计算机图形学对析出-长大微观过程进行图形化表征,体现出较好优势。如TIKARE等[12-13]利用MC方法并借助于Potts模型,对液相内溶质聚集、析出、Ostwald熟化长大的微观过程进行了模拟,所得颗粒溶解尺寸与其饱和浓度之间能够较好地符合Gibbs-Thomson关系,并认为该方法模拟得到的颗粒熟化长大过程受扩散机制控制。并通过改进模拟规则,使颗粒熟化长大指数更接近于扩散机制控制下的理论长大指数1/3,且其数值不随温度、液相含量等模拟条件变化而出现较大波动。LIU[14]、LEE等[15]和LUQUE等[16]则将MC方法从模拟液相析出-长大过程衍生至模拟液相烧结过程。杨卫兵等[17]和朱阁等[18]还将MC方法用于模拟低饱和度溶液内单晶表面的溶质析出行为,通过控制溶液浓度、单晶表面状态等因素,模拟得到了基于单核/多核生长模式的二维成核生长动力学过程。
然而,在上述文献报道中,并没有考虑在过饱和液相内形核析出时存在临界形核尺寸、以及析出后会引起液相浓度下降、进而影响临界形核半径等因素,因此,其模拟结果并不能真实准确地反映实际析出-长大行为。为此,本文作者采用MC方法,首先针对过饱和液相体系内的析出-长大过程,制定合理的MC模拟规则;然后引入临界形核尺寸,用于分析随模拟时间延长得到的模拟数据,对晶胚、晶核、析出颗粒等微观连续区域进行区分,并考虑液相浓度变化对临界形核尺寸方面的影响因素;最终获得析出-长大过程中液相浓度、过饱和度、形核率、析出颗粒数量及其尺寸等模拟结果随模拟时间延长而呈现出的规律,并对其进行相关验证。
1 模拟过程描述
1.1 初始模拟对象构建
为了模拟过饱和液相内的析出-长大行为,基于二维矩阵建立一个离散型的模拟对象:首先定义m×m的二维矩阵L,并预设液相初始浓度值c0;然后在矩阵L中随机选取c0×m2个互不相邻的格点,将整数序列[1,c0×m2]中的每一个整数值依次赋予这些格点,用于标示溶质,将数值-1赋予剩余的矩阵格点,用于标示液相区域;最后经图形化处理后得到如图1所示的初始模拟对象。
1.2 模拟体系界面能评估
在模拟过程中,受模拟规则驱动,矩阵内的单个溶质格点会发生团聚、继而形成晶胚/临界晶核/析出颗粒等连续区域(由多个状态值相同且位置相邻的溶质格点组成),或者晶胚/临界晶核/析出颗粒重溶形成溶质。整个模拟体系界面能E的计算如下[12]:
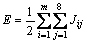 (1)
(1)
式中:m为矩阵L的边长;i和j代表相邻的两个矩阵格点,Jij为i和j之间的单位界面能,其定义如下[13]:i和j为状态值不同的相邻固相格点时,Jij等于单位固-固界面能Jgb;i和j为相邻的固相-液相格点时,Jij等于单位固-液界面能为Jsl;i和j为状态值相同的相邻格点时,Jij等于0,即不存在界面能。
1.3 模拟规则描述
在本研究中,针对的模拟过程如下:含一定溶质浓度的液相迅速降至某一温度后,达到过饱和状态,继而发生溶质析出-长大,其中包含溶质扩散、溶质聚集(形成晶胚/晶核/析出颗粒等连续区域)、以及晶胚/晶核/析出颗粒溶解(形成溶质)等微观过程。为了模拟这几类微观过程,在矩阵L中随机选取一对相邻的固相格点A/液相格点B,并根据格点状态不同,尝试变化A和B的格点状态:首先改变固相格点A的状态值,然后交换相邻固相格点A与液相格点B之间的状态值。相关模拟规则描述如下。
1) 若固相格点A/液相格点B周围均为液相格点(即A为溶质格点),则尝试直接交换两者状态值,用于模拟溶质在液相中扩散的微观行为(见图2(a))。
2) 若固相格点A周围均为液相格点(即A为溶质格点),而液相格点B周围存在其他固相格点,则从这些固相格点中随机选取某一固相格点A′,先尝试将A′的状态值赋予A,然后交换A与液相格点B之间的状态值,用于模拟溶质在液相中聚集、形成晶胚/晶核/析出颗粒等连续区域的微观行为(见图2(b))。
3) 若固相格点A周围存在状态值与A相同的其它固相格点(即A属于某一晶胚/晶核/析出颗粒等连续区域),则尝试将某一新固相状态值赋予A,其中该新状态值与液相格点B周围所有的固相格点状态值均不同,用于模拟晶胚/晶核/析出颗粒等连续区域溶解形成溶质格点的微观行为(见图2(c))。
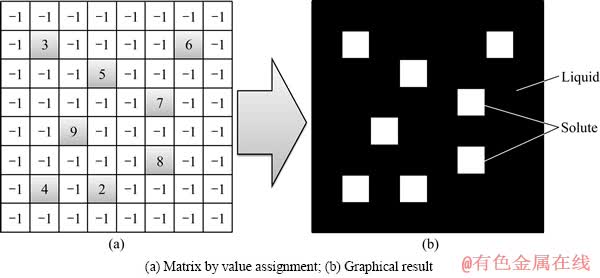
图1 基于二维矩阵建立的初始模拟对象
Fig. 1 Initial simulation object based on two-dimensional matrix to simulate precipitation-growth process in supersaturated solution
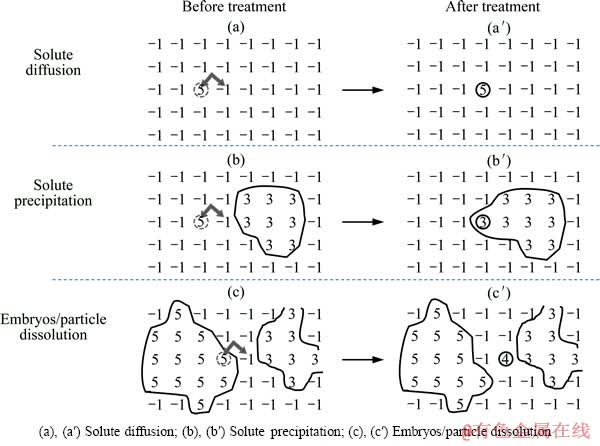
图2 过饱和溶液内几类微观过程的模拟实现示意图
Fig. 2 Sketch to realize simulation of several micro-processes in supersaturated solution
为了判断上述变化格点状态值的尝试过程是否被接受,需要根据式(1)计算由此引起的模拟体系界面能变化ΔE=E2-E1,E1和E2分别为尝试前后的体系界面能,并计算对应的Boltzmann概率P:
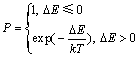 (2)
(2)
式中:k为Boltzmann常数,T为模拟温度。若ΔE≤0,则接受尝试过程,并相应变化/交换格点状态值。若ΔE>0,则在(0, 1)产生一个随机数W:当P≥W时,同样接受变化/交换格点状态值的尝试,否则矩阵格点仍保持原有状态值。对模拟矩阵L中的所有格点遍历处理一次,即为一个模拟时间步tMCS,所得数据用于后续分析处理。
1.4 模拟结果分析
在目前关于MC模拟液相析出-长大过程或者液相烧结过程的文献报道中,均只将单个溶质格点视为溶质,而将由多个状态值相同且相邻的溶质格点组成的连续区域都视为析出颗粒(见图2)[12-16]。然而对于 实际过饱和液相体系,形核过程存在临界形核半径r*,具有临界形核半径r*的晶胚被称为临界晶核:只有当溶质聚集在一起的尺寸大于r*,才会进一步析出形成固相颗粒。可见,由多个状态值相同且位置相邻的溶质格点组成的连续区域有可能仍为晶胚,而并非析出颗粒。临界形核半径r*与过饱和浓度c之间存在如下关系:
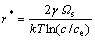 (3)
(3)
式中:γ为固相与液相之间的比界面自由能,Ωs为单个原子体积(Ωs取值为1,即代表单个溶质格点),ce为液相平衡浓度。在MC模拟过程中,为了引入临界形核半径,并用于区分模拟矩阵内的晶胚区域和析出颗粒区域,在本研究中,首先设定用于分析第1模拟时间步内所得模拟数据的液相浓度c1,以及此时临界球形晶核包含的溶质格点数量n1个,临界形核半径r1*=(n1/π)1/2。将r1*、γ、c1、Ωs和kT等参数代入式(3),计算得到平衡浓度ce。在处理第1模拟时间步内得到的模拟数据时,利用n1对由多个状态值相同且位置相邻的溶质格点组成的连续区域进行识别:由小于n1个溶质格点组成的连续区域为溶质/晶胚,把所有溶质/晶胚区域包含的矩阵格点总数除以液相格点总数,即为完成第1模拟时间步、在第2模拟时间步达到的液相浓度c2;由大于n1个溶质格点组成的连续区域为析出颗粒,统计其数量即为形核数量,并可求得此时的析出颗粒平均尺寸。在处理第2模拟时间步内所得模拟结果时,首先利用前面获得的c2和ce,并根据式(3),求得r2*以及此时临界球形晶核包含的溶质格点数量n2=πr2*2;然后同样利用n2对矩阵内的溶质/晶胚区域和析出颗粒区域进行识别,获得形核数量、析出颗粒平均尺寸、第3模拟时间步内达到的液相浓度c3等数据。后续模拟时间步内所得模拟数据的处理均按上述前后模拟时间步之间的递推关系进行(流程见图3),进而获得液相浓度、形核数量/析出颗粒数量、形核率、平均颗粒尺寸等随模拟时间延长呈现出的变化规律。模拟过程中采用如下参数:矩阵L的边长m=200,初始液相浓度c1=17.5%,临界球形晶核包含的溶质格点数n1=4,单位晶界能Jgb=2.5,单位固-液界面能Jsl=1.0,Ωs=1,kT=1.3~1.8。
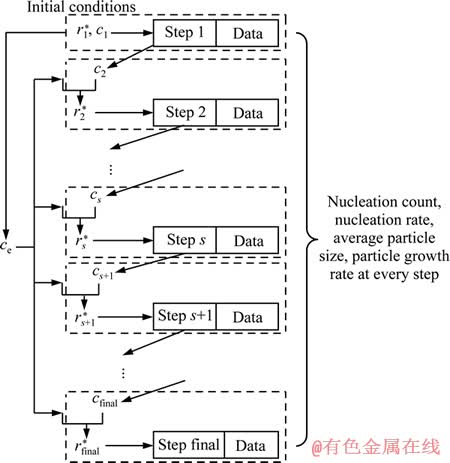
图3 模拟结果处理及提取流程图
Fig. 3 Flow chart of treatment and extraction of simulation results
2 结果与讨论
2.1 形核-析出过程的图形模拟结果
图4给出了Jgb=2.5/Jsl=1.0、采用不同kT值得到的模拟结果,其中黑色区域代表液相分布状态,白色区域则被视为溶质/晶胚或者析出颗粒。
由图4可以发现,在kT数值相对较高(kT=1.8)的模拟条件下,随着模拟时间延长,模拟区域内没有发生明显的溶质格点聚集并形成白色等轴状连续区域(见图4(a))。随着模拟温度的降低(kT<1.8),溶质格点聚集形成白色连续区域的现象逐渐明显:在模拟时间相同的条件下,模拟温度越低,白色连续区域形成数量越多、面积越小;在kT相同的条件下,模拟时间越长,白色连续区域形成数量越少、面积越大,即发生Ostwald熟化长大现象(见图4(b)~(d))。
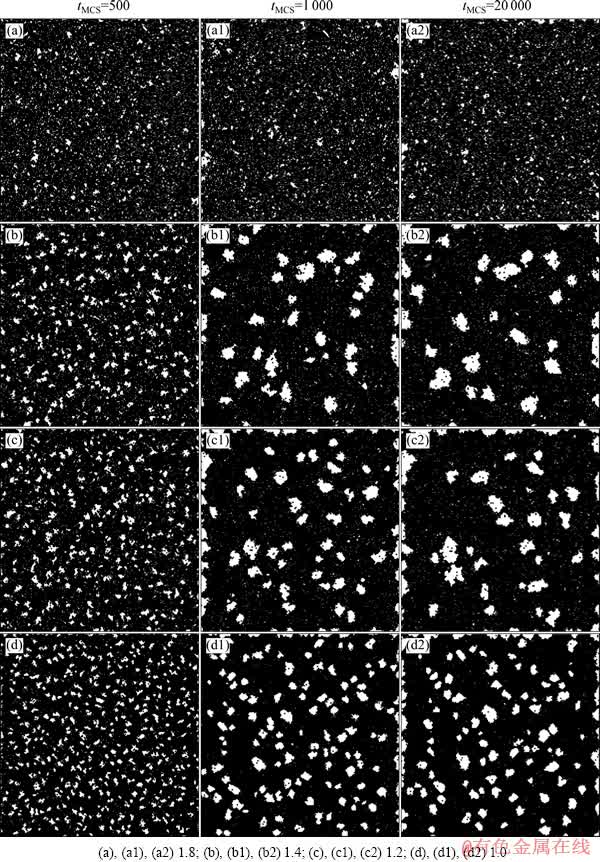
图4 采用不同kT值得到的析出-长大过程图形模拟结果
Fig. 4 Graphic simulation results of precipitation-growth process by using several kT values, kT
对于未达到饱和浓度的实际液相体系,其浓度会随温度降低而减小,并逐渐经历“欠饱和-饱和-过饱和”等状态。液相只有达到过饱和状态才会发生形核析出,其驱动力为过饱和度[1]。当降温至液相仍未达到过饱和状态时,不会发生形核析出的现象,在模拟结果中表现为:采用相对较高的kT值不会在模拟区域 内形成溶质格点聚集而成的连续区域(见图4(a))。温度 进一步降低、直至使液相进入过饱和状态时,形成的过饱和度作为形核驱动力,驱使形核析出发生,其中温度下降越多,则过饱和度及形核驱动力越大,也越容易发生形核析出。这在模拟结果中表现为:降低模拟温度引起白色连续区域形成数量增多(见图4(b)~(d))。进一步延长模拟时间后,液相内主要发生析出颗粒的Ostwald熟化长大:小颗粒优先溶解,形成的溶质在大颗粒表面析出,促使大颗粒进一步长大,析出颗粒数量减少,体系固-液界面能降低。在模拟结果中出现相似的现象:模拟时间越长,连续区域形成数量越少、尺寸越大。另外,图5所示为NiO+Fe2O3先在1 200 ℃的KCl熔盐内反应4 h、然后急剧降至不同温度并保温4 h后所得NiFe2O4产物颗粒的显微形貌,其中反应物NiO与Fe2O3的摩尔比为1:1、反应物与KCl的质量比为1:1,并且为了抑制KCl的高温挥发,采用了双层坩埚:将混合好的NiO+Fe2O3+KCl颗粒放在内层小坩埚中,内层小坩埚和外层大坩埚之间填放一些KCl颗粒,并且在两个坩埚上均盖有Al2O3陶瓷片。由图5可以发现,温度下降越少,则KCl熔盐过饱和度越大、形核率越高,由此引起NiFe2O4产物颗粒尺寸减小、数量增多。可见,图形模拟结果中的析出-长大现象与实际液相体系在降温延时过程中的表现较为一致。

图5 NiO+Fe2O3先在1 200 ℃的KCl熔盐内反应4 h、然后急剧降温至850 ℃和1 100 ℃并保温4 h后所得NiFe2O4产物颗粒的显微形貌
Fig. 5 Morphologies of NiFe2O4 particles obtained by reaction of NiO and Fe2O3 in KCl flux at 1 200 ℃ for 4 h, followed by rapidly decreasing to 850 ℃ (a) and 1 100 ℃ (b) and holding for 4 h
2.2 液相浓度及过饱和度
图6给出了Jgb=2.5/Jsl=1.0、采用不同kT值得到的液相浓度—模拟时间曲线。由图6可以发现,无论采用何种kT值,液相浓度均随模拟时间延长呈现出急剧下降、缓慢下降、最后趋于稳定并达到平衡的变化趋势;模拟温度越低,则对应的平衡浓度越低,且达到平衡浓度所需的模拟时间越长。另外,表1所列为将n1和kT代入式(3)计算所得、以及利用模拟数据绘制液相浓度—模拟时间曲线所得不同模拟温度条件下的平衡浓度数值,可以发现两者数值较为吻合。
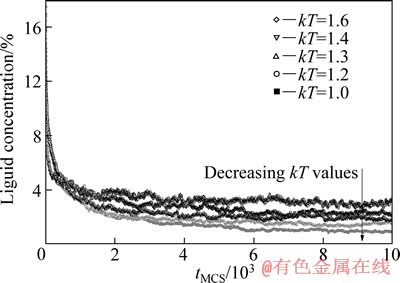
图6 采用不同kT值得到的液相浓度—模拟时间曲线
Fig. 6 Curves of liquid concentration versus simulation time by using several kT values
表1 通过计算和模拟得到的液相平衡浓度ce数值对比
Table 1 Equilibrium liquid concentration values obtained from calculation and simulation
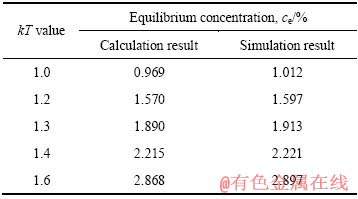
在模拟初始阶段,模拟矩阵中存在大量被液相格点包围的溶质格点。受MC模拟规则驱动,这些溶质格点很容易聚集在一起,达到降低体系能量的模拟目的,并在模拟矩阵中迅速形成晶胚、晶核、乃至析出颗粒等连续区域。大于临界形核尺寸的连续区域均被视为析出颗粒,被排除到液相浓度统计之外,被视为溶质的格点数量迅速减少,液相浓度大幅降低。模拟时间进一步延长后,由于许多溶质格点已聚集在一起形成连续区域,剩余溶质与连续区域之间的距离增加,需要经历多个模拟步(即与相邻液相格点多次交换)后,才能与某些连续区域毗邻、继而完成析出模拟,即交换扩散距离的增加减缓了溶质析出速率和液相浓度降低速率。与此同时,对于模拟前期形成、被识别为析出颗粒的连续区域,通过尝试交换其所属固相格点与相邻液相格点之间的状态后,有可能形成新的溶质,这也部分抵消了由溶质析出引起的浓度降低幅度。上述两种因素均导致液相浓度随模拟时间进一步延长而缓慢下降。当连续区域通过溶解模拟形成溶质、以及溶质通过析出模拟发生聚集析出这两类微观模拟行为达到动态平衡时,液相浓度趋于稳定。另外,在尝试从连续区域剥离出固相格点、进而形成溶质的模拟过程中,会形成新的固-液界面,即此过程引发的ΔE>0。而当整个模拟过程中采用的kT值降低时,由式(2)可知,ΔE>0对应的Boltzmann交换概率相应减小,即从连续区域剥离出固相格点并形成溶质的难度增加,液相浓度减小(见图6)。在本研究中,获得的液相浓度降低模拟现象与实际析出过程较为一致。
为了进一步验证模拟结果与实际过饱和液相析出过程之间的一致性,图7(a)中给出了在不同kT值条件下得到的液相过饱和率c/ce—模拟时间曲线,并利用文献[19]报道的SrMoO4过饱和溶液析出实验结果(见图7(b))进行对比。由图7(a)可以发现,液相的过饱和度在模拟初期急剧下降,随模拟时间进一步延长而缓慢下降并直至趋近于1,液相浓度趋近于平衡浓度ce;随着kT值的增加,液相过饱和度达到平衡状态所需的模拟时间缩短。图7(b)中所示的SrMoO4过饱和溶液析出过程实验结果也表现出与上述模拟结果一致的规律:在形核初期,溶液过饱和浓度相对较高,即形核驱动力较大,临界形核半径较小,溶质更容易聚集并析出,引起溶液过饱和度均急剧下降;而溶液过饱和度降低使得形核驱动力相应减小,临界形核半径增大,即溶质自身在溶液中聚集析出的难度增加,而逐渐转变为扩散并析出至颗粒表面,导致溶液过饱和度均下降缓慢,直至趋于稳定。
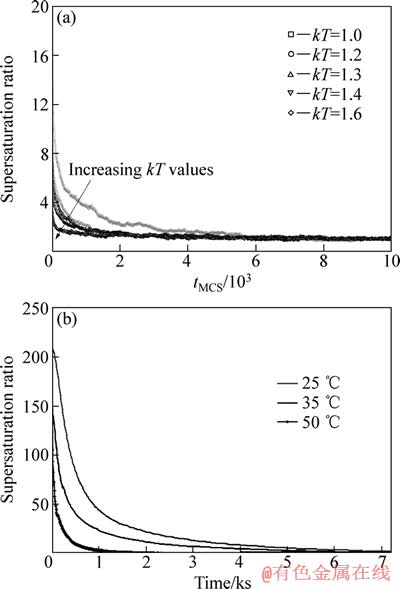
图7 采用不同kT值得到的液相过饱和率—模拟时间曲线及其与SrMoO4溶液析出过程实验结果的对比[19]
Fig. 7 Curves of supersaturation ratio versus simulation time at different kT values in this study (a), and experimental results for precipitation of SrMoO4 solution (b)[19]
2.3 颗粒析出长大过程
图8给出了Jgb=2.5/Jsl=1.0、采用不同kT值得到的平均析出颗粒半径—模拟时间曲线。由图8可以发现,在采用相同的模拟温度时,析出颗粒平均半径Raverage随模拟时间tMCS延长呈抛物线形式Raverage=AtMCSm(m为长大指数)增长;当升高模拟温度时,析出颗粒的长大趋势增强。平均析出颗粒半径是通过统计模拟矩阵内的析出颗粒总数以及每个析出颗粒尺寸后、经平均计算得到的,而模拟形核率和溶质格点交换扩散-析出速率则分别决定了析出颗粒数量和长大尺寸。如前所述,在模拟初始阶段,模拟矩阵中的溶质格点受MC模拟规则驱动而易于发生聚集,并迅速形成晶胚、晶核、乃至析出颗粒等连续区域,以降低体系固-液界面能。当采用相对较大的kT数值时,由式(2)可以发现,用于判定固相格点能否从其所属连续区域表面剥离、继而形成溶质格点的Boltzmann交换概率相应增加,即更容易发生连续区域被液相溶解形成溶质的模拟事件,进而也更难使连续区域面积超过模拟设定的临界形核尺寸而被视为析出颗粒。另外,由式(3)可知,随后过饱和浓度的逐渐降低又会导致临界形核尺寸逐渐增加,这又进一步增大了连续区域受溶质格点析出后达到临界晶核尺寸、直至被视为析出颗粒的难度。上述两方面原因均导致形核率随模拟温度的升高而降低,统计得到的析出颗粒总数减少。随着模拟时间的进一步延长,同样受基于Boltzmann概率判定的模拟规则驱动,采用较大的kT数值会促使溶质格点在液相区域内发生交换扩散、直至析出到已稳定存在于模拟矩阵内、且因其面积大于临界形核尺寸而被视为析出颗粒的连续区域表面,以实现固-液界面能尽快降低,进而引起更快的析出颗粒长大速率。由此可见,由模拟温度升高引起的形核率降低、以及溶质交换扩散-析出速率r增加,均导致平均析出颗粒半径呈现出更快的增长趋势。当连续区域溶解形成溶质、以及溶质析出逐渐达到模拟动态平衡时,平均析出颗粒半径的增长趋势逐渐减弱,直至趋于稳定。这与图5中显示的液相降温越低、则析出产物数量越多且尺寸越小的实际规律相吻合。
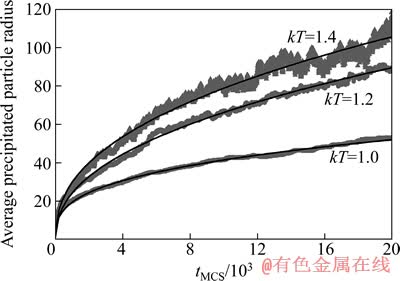
图8 采用不同kT值得到的平均析出颗粒半径—模拟时间曲线
Fig. 8 Curves of average precipitated particle radius versus simulation time at different kT values
对上述采用不同kT值获得的平均析出颗粒半径—模拟时间曲线进行非线性拟合,可以得到析出颗粒长大指数m分别为0.320(kT=1.0)、0.328(kT=1.2)和0.332(kT=1.4)。TIKARE等[13]指出,通过此类MC模拟方式得到的析出颗粒Ostwald熟化长大受扩散过程控制,其理论颗粒长大指数为1/3;且通过合理改进模拟规则,使模拟所得颗粒长大指数不随温度、液相含量等模拟条件变化而发生较大波动,其中不同模拟条件下得到的颗粒长大指数数值分布在0.30~0.31之间。而在本研究中模拟得到的颗粒长大指数更接近于理论颗粒长大指数1/3,且采用不同kT得到的指数数值较为一致。
3 结论
1) 当采用较高的模拟温度时,较难发生明显的溶质格点聚集和颗粒析出。模拟温度进一步降低后,溶质格点聚集析出现象逐渐明显:温度越低,则溶质格点聚集析出的数量越多、面积越小;模拟时间越长,则析出数量越少、面积越大,即发生了Ostwald熟化长大。析出-长大图形模拟结果与对NiFe2O4-KCl熔盐体系降温延时得到的实验现象相符。
2) 模拟所得液相浓度、过饱和度均随模拟时间延长呈现出急剧下降、缓慢下降、最后趋于稳定并达到平衡的变化趋势,且模拟温度越低,平衡浓度数值越低,达到平衡浓度所需的模拟时间越长。通过对比SrMoO4过饱和溶液的析出实验结果,表明模拟结果与实验结果较为一致。
3) 在平均析出颗粒半径—模拟时间曲线中,采用相同模拟温度时,析出颗粒的平均半径随模拟时间延长呈抛物线增加,升高模拟温度则会加速析出颗粒的长大趋势,各种模拟温度下得到的颗粒长大指数在0.320~0.332之间,且不随模拟温度变化发生较大波动,与受扩散过程控制下的颗粒Ostwald熟化长大机制吻合。
REFERENCES
[1] 姚连增. 晶体生长基础[M]. 合肥: 中国科学技术大学出版社, 1995: 266-267.
YAO Lian-zeng. Foundation of crytal growth[M]. Hefei: University of Science and Technology of China Press, 1995: 266-267.
[2] 薛 平, 田庆华, 郭学益. 化学共沉淀-热分解法制备Sm2Fe17合金前驱体[J]. 中国有色金属学报, 2008, 18(1): 341-347.
XUE Ping, TIAN Qing-hua, GUO Xue-yi. Preparation of Sm2Fe17 alloy precursor by chemical coprecipitation- decomposition method[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(1): 341-347.
[3] 瞿晓岳, 朱宏伟, 谢 辉, 陈振兴. 溶胶-凝胶法制备SiO2包覆型水性铝粉[J]. 中国有色金属学报, 2010, 20(6): 1241-1246.
QU Xiao-yue ZHU Hong-wei, XIE Hui, CHEN Zhen-xing. Waterborne aluminum powders coated with SiO2 by sol-gel method[J]. The Chinese Journal of Nonferrous Metals, 2010, 20(6): 1241-1246.
[4] ZHAO Shi-xi, LI Qiang, WANG Lin, ZHANG Yi-ling. Molten salt synthesis of lead lanthanum zirconate titanate stannate powders and ceramics[J]. Materials Letters, 2006, 60: 425-430.
[5] WANTHA L, FLOOD A E. Crystal growth rates and secondary nucleation threshold for γ-DL-methionine in aqueous solution[J]. Journal of Crystal Growth, 2011, 318(1): 117-121.
[6] YU X L, SUN Y, HOU W B, ZHANG S J, CHENG Z X. Interface kinetics and crystal growth mechanism of a new organometallic coordination compound: Triallylthiourea mercury bromide[J]. Journal of Crystal Growth, 1997, 182: 428-433.
[7] 卢贵武, 李春喜, 王子镐, 夏海瑞, 孙大亮, 于锡玲, 关继腾. KDP晶体台阶生长动力学的激光干涉实验研究[J]. 化学物理学报, 2003, 16(4): 289-292.
LU Gui-wu, LI Chun-xi, WANG Zi-hao, XIA Hai-rui, SUN Da-liang, YU Xi-ling, GUAN Ji-teng. A study on the step growth kinetics of KDP crystal by Michelson laser interferometer experiment[J]. Chinese Journal of Chemical Physics, 2003, 16 (4): 289-292.
[8] TSEKOVA D, DIMITROVA S, NANEV C N. Heterogeneous nucleation (and adhesion) of lysozyme crystals[J]. Journal of Crystal Growth, 1999, 196(2/4): 226-233.
[9] ISHIGURO R, CAUPIN F, BALIBAR S. Homogeneous nucleation of crystals by acoustic waves[J]. Europhysics Letters, 2006, 75(1): 91-97.
[10] OHTAKI H. Molecular dynamic approaches and supporting solution X-ray diffraction measurements[J]. Pure and Applied Chemistry, 1993, 65(2): 203-211.
[11]  L, PUSZTAI T, SAYLOR D, WARREN J A. Phase field theory of heterogeneous crystal nucleation[J]. Physical Review Letters, 2006, 98(3): 035703-1-4.
L, PUSZTAI T, SAYLOR D, WARREN J A. Phase field theory of heterogeneous crystal nucleation[J]. Physical Review Letters, 2006, 98(3): 035703-1-4.
[12] TIKARE V, CAWLEY J D. Application of the Potts model to simulation of Ostwald ripening[J]. Journal of the American Ceramic Society, 1998, 81(3): 485-491.
[13] TIKARE V, CAWLEY J D. Numerical simulation of grain growth in liquid phase sintered materials—I. Model[J]. Acta Materialia, 1998, 46(4): 1333-1342.
[14] LIU Po-liang. The relation between the distribution of dihedral angles and the wetting angle during liquid phase sintering[J]. Computational Materials Science, 2006, 36: 468-473.
[15] LEE S B, RICKMAN J M, ROLLETT A D. Three-dimensional simulation of isotropic coarsening in liquid phase sintering (I): A model[J]. Acta Materialia, 2007, 55: 615-626.
[16] LUQUE A, ALDAZABAL J, MARTINEZ-ESNAOLA J M, MARTIN-MEIZOSO A, SEVILLANO J G, FARR R S. Geometrical Monte Carlo model of liquid-phase sintering[J]. Mathematics and Computers in Simulation, 2010, 80: 1469-1486.
[17] 杨卫兵, 孙立功, 卢贵武. 溶液中晶体生长动力学的MC计算机模拟研究[J]. 原子与分子物理学报, 2003, 20(3): 429-433.
YANG Wei-bing, SUN Li-gong, LU Gui-wu. Computer simulation of crystal growth kinetics from solution[J]. Chinese Journal of Atomic and Molecular Physics, 2003, 20(3): 429-433.
[18] 朱 阁, 卢贵武, 李英峰, 蓝建慧, 张 军, 郑庆彬, 黄乔松, 孙 洵, 夏海瑞. 晶体生长机制和生长动力学的蒙特卡罗模拟研究[J]. 人工晶体学报, 2006, 35(1): 24-31.
ZHU Ge, LU Gui-wu, LI Ying-feng, LAN Jian-hui, ZHANG Jun, ZHENG Qing-bin, HUANG Qiao-song, SUN Xun, XIA Hai-rui. Monte Carlo simulation study on crystal growth mechanism and kinetics[J]. Journal of Synthetic Crystals, 2006, 35(1): 24-31.
[19] CAMEIRA A, DAVID R, ESPITALIER F, GRUY F. Effect of precipitation conditions on the morphology of strontium molybdate agglomerates[J]. Journal of Crystal Growth, 2008, 310: 4152-4162.
(编辑 龙怀中)
基金项目:国家重点基础研究发展计划资助项目(2005CB623703);中南大学博士后科学基金资助项目(2009年)
收稿日期:2012-05-16;修订日期:2013-06-30
通信作者:张晓泳,助理研究员,博士;电话:0731-88830464;E-mail:zhangxiaoyong@csu.edu.cn