J. Cent. South Univ. (2016) 23: 2036-2047

DOI: 10.1007/s11771-016-3260-4

Cross-coupling integral adaptive robust posture control of a pneumatic parallel platform

ZUO He(左赫), TAO Guo-liang(陶国良)

State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: A pneumatic parallel platform driven by an air cylinder and three circumambient pneumatic muscles was considered. Firstly, a mathematical model of the pneumatic servo system was developed for the MIMO nonlinear model-based controller designed. The pneumatic muscles were controlled by three proportional position valves, and the air cylinder was controlled by a proportional pressure valve. As the forward kinematics of this structure had no analytical solution, the control strategy should be designed in joint space. A cross-coupling integral adaptive robust controller (CCIARC) which combined cross-coupling control strategy and traditional adaptive robust control (ARC) theory was developed by back-stepping method to accomplish trajectory tracking control of the parallel platform. The cross-coupling part of the controller stabilized the length error in joint space as well as the synchronization error, and the adaptive robust control part attenuated the adverse effects of modelling error and disturbance. The force character of the pneumatic muscles was difficult to model precisely, so the on-line recursive least square estimation (RLSE) method was employed to modify the model compensation. The projector mapping method was used to condition the RLSE algorithm to bound the parameters estimated. An integral feedback part was added to the traditional robust function to reduce the negative influence of the slow time-varying characteristic of pneumatic muscles and enhance the ability of trajectory tracking. The stability of the controller designed was proved through Laypunov’s theory. Various contrast controllers were designed to testify the newly designed components of the CCIARC. Extensive experiments were conducted to illustrate the performance of the controller.

Key words: servo-pneumatic system; pneumatic muscle; parallel platform; cross coupling; adaptive robust control; parameter estimation

1 Introduction

Pneumatic muscles are biomimetic pneumatic actuators which use energy form compressed air to perform linear contraction. A pneumatic muscle usually consists a metal net made of helically braided fibers and a rubber bladder enclosed by two metal ends in both sides. When the pneumatic muscle is inflated, the inner volume of the rubber bladder increases with the angle of the braided fibers changing and the length remaining still, resulting in contraction and tension [1]. Pneumatic muscles have higher stiffness and less dead zone caused by friction compared with traditional pneumatic cylinders. So in most cases, the motion of pneumatic muscles is smoother and easier to control [2-3].

Pneumatic muscles have been applied in many recent researches, such as pneumatic servo parallel platforms. SHI and WEI [4] designed a parallel platform driven by three pneumatic muscles with a spring in the middle. Fuzzy control strategy with an adaptive part was employed in his research. With the model-free control strategy, the controller achieved a limited precision of posture trajectory tracking control [4]. YANG et al [5] designed an asymmetrical parallel platform driven by three pneumatic muscles. Synovial fuzzy controller was designed to control the posture of the moving plate. A parallel robot was designed for ankle rehabilitation, which was driven by two pairs of pneumatic muscles controlled by a fuzzy controller [6]. KHOA [7] designed a creative parallel platform driven by three pairs of pneumatic muscle-spring structures. ZHAO and BIN [8] designed a parallel mechanism for imitating human pelvis driven by four pneumatic muscles. The feasible operation performance of the platform was just analyzed in simulation. ZHU [9] designed a two-DOF parallel platform driven by three pneumatic muscles with a redundant DOF. An equivalent average-stiffness-like desired factor was introduced to eliminate the redundant DOF. An adaptive robust controller was designed to accomplish the trajectory tracking control. The platform performed well with a high level of control precision in a relative slow speed [9].

Cross-coupling method is a way to replace the traditional control errors with the coupling errors which contains original errors and synchronous errors. The original idea of equal-status cross-coupling strategy came from KOREN in 1980 [10]. Experimental results showed the cross coupling between axes can improve the control accuracy significantly compared with the conventional individual control system. After that, cross-coupling control strategy was widely studied by many researchers.

SUN et al [11] did a lot of work on study of cross-coupling control strategy, and proved that the cross-coupling control strategy works well on synchronous control of individual servo systems [11-12], parallel structures driven by multiple actuators [13-15] and multi-axis motion of one actuator [16]. SHAN et al [17] designed a cross-coupling synchronized controller of multiple 3-DOF experimental helicopters. A PD controller with a feed-forward compensation was used in trajectory tracking control of the parallel structure. XIAO et al [18-19] proposed a LQG optimal controller combined with the cross-coupling strategy in control of a multi-axis motion system. ZHAO et al [20-21] designed several robust synchronized controllers in study with four individual robot arms and a 6-SPS parallel platform.

A pneumatic parallel platform driven by three pneumatic muscles and a pneumatic cylinder is considered in this work. The force characteristics of the pneumatic muscle is highly non-linear and complex, so a control strategy based on non-linear theory is needed. The parallel platform of this structure has no analytical forward kinematics solution, so the controller should be designed in joint space. As the motion of the parallel platform in real is much different from the motion in joint space, cross-coupling control strategy which converges the synchronous error of adjacent pneumatic muscles as well as the length error is employed. A direct-indirect adaptive robust controller combined with cross-coupling control strategy based on non-linear theory with an integral feedback part is designed as the CCIARC controller to accomplish the trajectory tracking control of the pneumatic servo parallel platform.

2 Modeling analysis

The structure of parallel platform driven by three pneumatic muscles and an air cylinder is shown in Fig. 1. The pneumatic muscles were circumferentially isometric hinged between the moving plate and the fixed plate. The piston rod of the pneumatic cylinder was hinged to the center of the moving plate, and the cylinder block was fastened to the center of the fixed plate. The moving plate had three degrees of rotational freedoms namely roll, yaw, and pitch; it also had one degree of translational freedom in the vertical direction. The pneumatic muscles and the air cylinder were controlled by three proportional directional valves and a proportional pressure valve respectively. The parallel platform in this structure can maintain adjustable steady stiffness while moving.

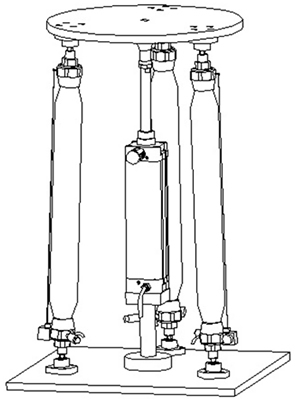
Fig. 1 Structure of parallel platform

The kinematic model of the parallel platform was a typical single joint. The center of the fixed plate was taken as the coordinate zero origin, and the center of the moving plate was taken as the coordinate one origin. The transitional matrix from the state variables in working space to those in joint space is:

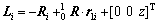                   (1)

where L_i was the length of the i-th pneumatic muscle; R_i was the position vector of the hinged joint between the i-th pneumatic muscle and the fixed plate in coordinate system zero; r_1i was the position vector of the hinged joint between the i-th pneumatic muscle and the moving plate in coordinate system one; z was the height of the moving plate; 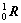was rotational transform matrix from coordinate one to zero.

The rotational dynamics of the moving plate is expressed as

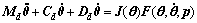              (2)

where M_d was the inertial matrix; C_d is the Coriolis torques; D_d is the damping matrix; J(θ) is the torque calculation matrix; θ is the RPY rotation angle vector.

The dynamics of the moving plate in the vertical direction is

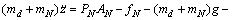
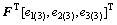    (3)

where m_d is the mass of the moving plate; m_N is the mass of the cylinder piston and its connector; P_N is the air pressure in the cylinder’s rodless cavity; A_N is the piston area of the cylinder; f_N is the friction force of the cylinder piston; E_i(3) is the vertical component of unit vector in the contractive direction of pneumatic muscles; F is the force vector of pneumatic muscles.

The force model of pneumatic muscles is highly nonlinear and affected by various factors. A complex force model as Eq. (4) was employed [22-23].

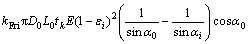 (4)

where p is the air pressure of pneumatic muscles; ε is the contractive ratio of pneumatic muscles; D and L are diameter and length of pneumatic muscles, when subscript 0 referred to the ordinary condition; k_Fri is the force correction factor; α is the braided angle of pneumatic muscles. Other variables are related to the structure of pneumatic muscles.

The friction of the air cylinder had been modeled in various static and motive ways. The Stribeck model was a practical static model which didn't require the dynamic analysis of friction factors and had the basic characteristics of friction, so it was used in the friction compensation. The Stribeck model employed in the controller is expressed as [24]

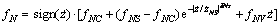 (5)

where f_NS is the maximum static friction force. f_NC is the Coulomb friction force; f_Nυ is the viscous friction coefficient; 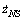is the Stribeck velocity; △Ns is the arbitrary exponent.

The polytropic equation was employed to modify the inner gas in pneumatic muscles. A pressure differential equation was used to describe the dynamic process of the gas in the pneumatic muscle chamber as [25]

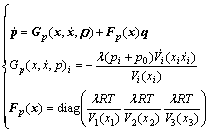            (6)

where q is the mass flow rate; λ is the polytropic index which is between 1 and 1.4; p₀ is the atmospheric pressure; R is the gas constant; T is the thermodynamic temperature; V_i is the volume of the inner chamber.

The flow model of one dominant orifice was used to describe the flow characteristics as [26]

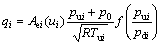                   (7)

where p and T are pressure and temperature of the gas, when subscripts u and d referred to the inlet and the outlet of the valve; A_e is the equivalent orifice area.

Three MPYE proportional directional overlapped valves of Inc. Festo were used to control the pneumatic muscles. The linearity of the MPYE valve outside the dead zone was high, so the model as Eq. (8) was employed.

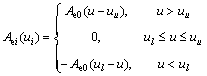            (8)

where A_e0 is the proportional ratio of the equivalent orifice area; u_u is the minimum input value when pneumatic muscles start to inflate; u_l is the maximum input value when pneumatic muscles started to deflate.

The air pressure of the rodless cavity was controlled by the MPPES proportional valve of Inc. Festo. A gas tank was added between the proportional valve and the cylinder to reduce pressure fluctuation. The set value of the proportional remained still while the parallel platform was moving. The linearly ratio from set value to desired pressure of the rodless cavity is expressed as

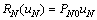                             (9)

where u_N is the set value of the proportional valve; P_N0 is the pressure factor of the proportional valve. The pressure of the rodless cavity was measured in real time, so the modeling error of Eq. (9) wouldn’t affect the controller.

The force characteristics of pneumatic muscles were related to both length and air pressure inside. The dynamic feature of the parallel platform varied much in different conditions of pneumatic muscles, so model-free controllers performed poorly, especially in trajectory tracking control. As the dynamic model of the parallel platform was highly non-linear and affected by many unmeasured factors, a controller based on non-linear control strategy with an adaptive ability was required in posture control of the parallel platform.

3 Controller design

An MIMO adaptive robust controller was designed through the back-stepping method [27]. The experimental schematic is shown in Fig. 2, in which u is the control vector of the proportional directional valves and u₀ is the control signal of the proportional pressure valve.

1) Step one

The movement of the moving plate in yaw was rather small and had little effect on other direction of movement, so it was neither observed nor controlled by the controller designed [28]. State variables in work space X equaled [θ_x θ_y z]^T, so the kinematic dynamics is expressed as

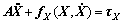                        (10)

The lengths of three pneumatic muscles were taken as the state variables in joint space as

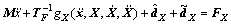        (11)

where M is the symmetric matrix which referred to the equivalent mass driven by each pneumatic muscle. The equivalent mass was assumed to equal one third of the total mass of moving plate and connector in order to represent the inertial character of the platform; 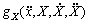was the nonlinear compensation part; 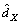was the uncertain model part which was measured by an adaptive control method in the following chapter. 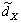was the error term of the uncertain part remained; F_X was the force vector of pneumatic muscles; T_F was the force transformation matrix.

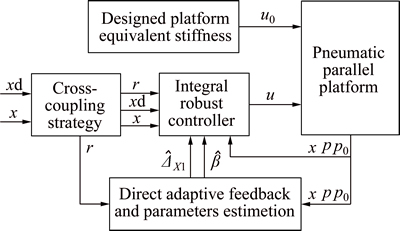
Fig. 2 Schematic of controller

The state error in joint space e equaled x_d-x, while x_d was the expectation state. Cross-coupling control strategy is taken into consideration as follows. With the synchronistic error ε=Te, the coupling error was expressed as

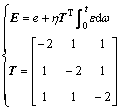                        (12)

where η is the coupling factor; T is the coupling matrix of which the sum of each line is zero in order to guarantee the stability of the controller.

A compound error vector was defined as 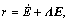in which 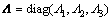was a positive diagonal matrix. E would converge to zero when r was zero according to the stable transfer function. The differential expression of r is

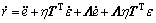                   (13)

An adaptive control strategy was employed to identify the unmeasured modeling error of the force feature of pneumatic muscles.

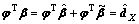                     (14)

where φ is the adaptive matrix;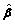is the adaptive coefficients vector; 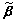is the adaptive error vector.

The remaining estimation error contained the slow time-varying disturbance △_X1 and fast time-varying disturbance △_X2. △_X1 is compensated by direct adaptive control part. △_X2 is restrained by the model uncertainty compensation part.

Some variables as Eq. (15) were defined to simplify the expression:

     (15)

where K_ε is a positive diagonal matrix of which the elements were the same to guarantee the stability of the controller designed.

The desired input force vector is expresed as

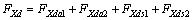             (16)

where F_Xda1 is the nonlinear compensation which equaled 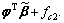Similar as the DCARC control method [29], f_c2 depending on reference trajectory was used in practical to simplify the controller. The compensation error caused by DCARC control method was compensated by the robust control part. F_Xda2 is the compensation of the slow time-varying disturbance which equaled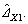 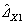is the estimation of 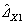, and 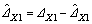is the estimation error.

F_Xds1 guaranteed the stability of the control system. F_Xds2 compensated the model uncertainty which satisfied the following inequalities:

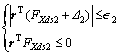                        (17)

The detailed expressions are as follows:

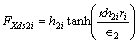                     (18)

where κ=0.2785, h_2i≥|△_2i|i.

This desired force vector could make the coupling error converge to a sphere with the radius relating to 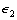, which meant the stability of the control system.

2) Step two

The controller was further designed to converge 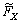to 0. The desired pressure of the inner gas of pneumatic muscles was calculated by Eq. (4).

According to Eq. (6), the dynamic pressure model of the inner gas is expressed as

                      (19)

where referred to the equivalent inflow mass rate; 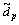represented the model error and disturbance.

p_d was the desired pressure of the inner gas in pneumatic muscles. Z₃=p_d-p was the pressure error, and its derivative was as

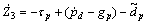                    (20)

Similar as in step one, f_c3 and △₃ were defined to simplify the expression.

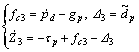                      (21)

The expecting pressure of the inner gas was as

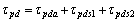                      (22)

τ_pda compensated the certain part of the nonlinear model. τ_pds1 guaranteed the stability of the control system. τ_pds2 compensated the model uncertainty which satisfied the following inequalities:

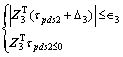                        (23)

The detailed expressions are as follows:

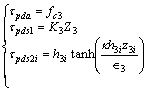                    (24)

where κ=0.2785, h_3i≥|△_3i|_i.

This expecting pressure could converge the coupling error and pressure error to a sphere with the radius relating to 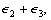which meant the stability of the control system. Based on Eqs. (7) and (8), desired equivalent area of the proportional valves and the control input could be easily calculated.

4 Parameter estimation

4.1 Direct adaptive estimation

A direct adaptive estimation method which was driven by control errors was employed to compensate the slow-time varying characters of pneumatic muscles.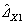was the estimation of △_X1, which was identified through the following adaptive low:

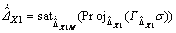               (25)

σ equaled r in this condition. A limitation 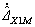in changing rate of 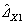was added as

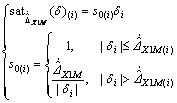                (26)

The projection mapping strategy as Eq. (27) was employed to keep the direct adaptive parameters within the known boundary.

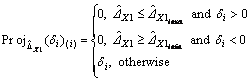     (27)

With this adaptive low designed,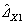could compensate part of the model error caused by the time-varying force character of pneumatic muscles.

4.2 Recursive least squares estimation

A recursive least squares estimation (RLSE) algorithm was employed to estimate the parameters in real time and reduce the dynamic model error. The parameters estimated should be bounded due to the proof of stability in appendix, so the projection mapping strategy is employed to keep the parameters within the known bounded convex.

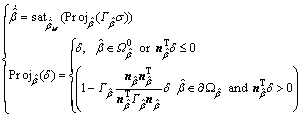 (28)

where 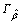is the learning rate of parameter estimation; σ is the parameter adaptive function; 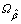is the forecast range of β.

Furthermore, to achieve a complete separation between the estimator and the robust controller design, an adapting rate limitation was added to the RLSE algorithm as

                      (29)

The inequalities could be derived as

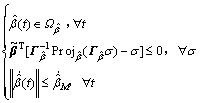            (30)

The system was assumed to be free of measuring error, then the adaptive estimation vector was designed as Eq. (31) according to Eqs. (11) and (15).

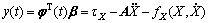           (31)

Coefficients in force model of pneumatic muscles used in the experiment were identified off-line, so only unmeasured model error remained to be estimated, which was described by polynomials of the length of pneumatic muscles. As force character of each pneumatic muscle was slightly different, the adaptive matrix was defined as Eq. (32).

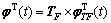                          (32)

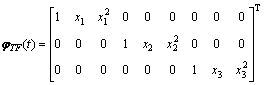  (33)

Acceleration signals were used in calculation of adaptive estimation error, so a stable LTI filter was added to both sides of Eq. (31) to reduce the effect of the measuring error. A three-degree Butterworth filter of which the normalization model was as Eq. (34) was employed as the LTI filter.

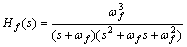              (34)

The stable LTI filter was applied in both sides of Eq. (31) as Eq. 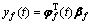(35).

                            (35)

The predicted adaptive estimation vector was defined as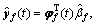leading to the following adaptive error vector:

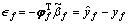                       (36)

                        (37)

The RLSE algorithm with forgetting factors and spectral radius saturation was applied in parameter estimation. The parameter estimation matrix rate and parameter adaptive function are defined as

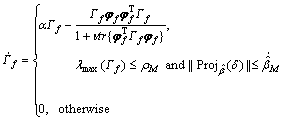(38)

α and v were forgetting factors of the RLSE algorithm. ρ_M was the maximum spectral radius of Γ_f. As the spectral radius was difficult to calculate, the upper bound of maximum spectral radius of Γ_f which was estimated by Gerschgorin Theorem was used instead. The i-th Gerschgorin plate was defined as

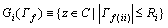                 (39)

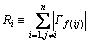                             (40)

The upper bound of the Gerschgorin plates as Eq. (41) was used to bound Γ_f.

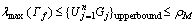            (41)

5 Experimental results

The experimental device is shown in Fig. 3. The parallel platform had three DOFs as roll, pitch and height. The moving plate was driven by three circumferentially equidistant pneumatic muscles and a pneumatic cylinder in center. The movement in the yaw direction was small and had little effect on the movement in other directions, so it was neither observed nor controlled.

Fig. 3 Experimental device

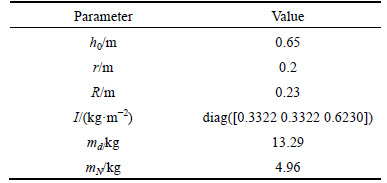
The cylinder with a diameter of 80 mm and a stroke of 0.25 m was controlled by a proportional pressure valve. The pneumatic muscles with diameters of 40 mm and initial lengths of 0.6 m were controlled by proportional directional valves. The pneumatic actuators and valves were all manufactured by Festo, Inc. The piston rod was radially fixed by an auxiliary fixation which was attached to the fixed plate. Linear displacement sensors were set up parallel to the pneumatic muscles to measure their length. Pressure sensors were used to measure the air pressures in the rubber bladders of the pneumatic muscles. The control algorithms were implemented by a dSPACE DS1103 controller board with an industrial computer as the user interface. The sampling period of the controller was set to 1 ms. The geometric parameters are listed in Table 1.

Table 1 Geometric parameters of platform

Two performance indices were employed as below to qualify control results of the parallel platform:

                      (42)

where |e_M| meant the maximum absolute value of the tracking error when the movement of the parallel platform came steady, during the last two periods of the sine signal specifically. T_f was the final running time, and T was the period of the tracking sine signal. It was employed to measure the final tracking accuracy of the parallel platform.

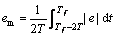
where e_m meant the mean value of the absolute tracking error when the movement of the parallel platform came steady, during the last two periods of the sine signal specifically. It was employed to measure the average tracking performance.

A complex sinusoidal signal which consisted of 8deg-amplitude sine signals in roll and pitch and a 50mm-amplitude sine signal in height was employed as the desired tracking signal. Control results of the CCIARC controller tracking various periods of sinusoid trajectories are listed in Table 2. Specifically, the control performance of the CCIARC controller in tracking the 10s-period sinusoidal trajectory is shown in Fig. 4. The control errors |e_M| and e_m were much smaller than those in most other studies. The history of on-line parameter estimations is shown in Fig. 5.

Extensive controllers were designed to testify the validity of the control strategies. Cross-coupling integral adaptive robust controller (CCIARC), integral adaptiverobust controller (IARC), cross-coupling adaptive robust controller (CCARC), adaptive robust controller (ARC) and traditional PD controller were applied to the parallel platform. e_m of the trajectory tracking control of the various controllers is shown in Fig. 6. As shown in Fig. 6, the effectiveness of the cross-coupling strategy and the integral part was significant.

Table 2 Sinusoidal tracking control results

Tracking errors in joint space and the synchronous errors were analyzed to testify the function of the cross- coupling strategy. e_xi was the tracking error in length of the i-th pneumatic muscle, and 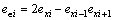was the synchronous error as Eq. (12). As shown in Fig. 7, the cross-coupling strategy did little effect on the direct tracking errors in joint space but decreased the synchronous errors significantly. The movement of the moving plate in the direction of row and pitch was related to synchronous errors more than direct errors in joint space, so the cross-coupling strategy could decrease the control error in the direction of row and pitch significantly as shown in Fig. 7.

A pseudo random signal was employed to testify the effectiveness of the CCIARC controller as well. The tracking signal consisted several sinusoidal signals in various periods. Tracking result is shown in Fig. 8. The tracking errors shown were similar to those in sin trajectory tracking.

To test the robustness of the controller designed, a metal plate with a mass of 4.90 kg was used to imitate the disturbance. The diameter of the metal plate was 127 mm, and the thickness was 52 mm. The plate was put on the moving plate of the parallel platform with its center at the spot of (-140 mm, 140 mm) on the moving coordinate at about 17 s and removed at about 53 s. The moving plate vibrated little when the load changed, and recovered quickly as shown in Fig. 9.

6 Conclusions

1) A cross-coupling integral adaptive robust controller which combined traditional adaptive robust controller and cross-coupling control strategy is designed to achieve the trajectory tracking control of a parallel platform driven by three pneumatic muscles and an air cylinder. The stability of the controller designed is verified through Lyapunov’s theory.

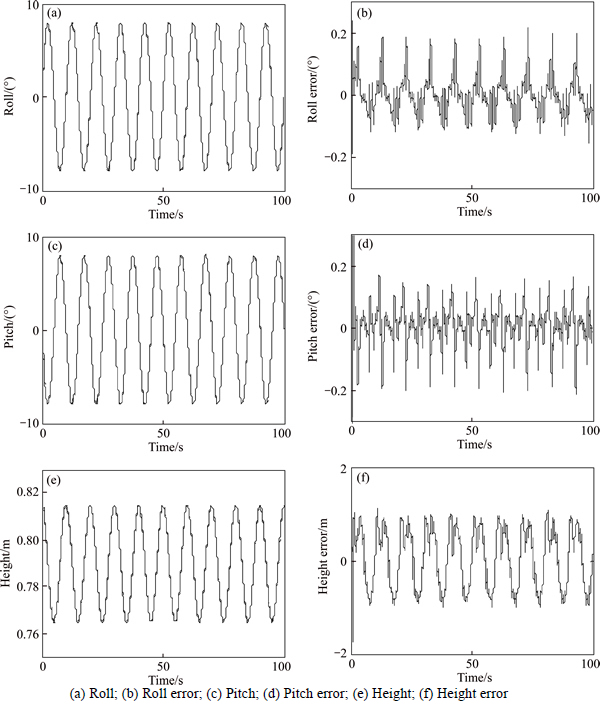
Fig. 4 Sinusoidal trajectory tracking:

2) The recursive least squares estimation algorithm is employed to identify the modelling error on-line as the adaptive component of the proposed controller. To insure the separation of the sliding mode control and the adaptive control designed, the projection mapping method with an adaptive rate limitation is used to condition the RLSE algorithm to keep the parameters within a predicted bounded convex.

3) Extensive experiments of various controllers are conducted for sinusoidal trajectory tracking to testify the function of the cross-coupling strategy and the integral robust feedback. The precision of trajectory tracking is much better than those of most other studies. A pseudorandom tracking experiment is also conducted to verify the validity of the CCIARC controller. A disturbance is added to the platform to testify the robustness of the CCIARC controller.

Appendix: Stability proof

A non-positive Lyaponov function which contained coupling errors and synchronous errors with their integral terms was defined as

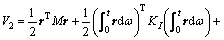
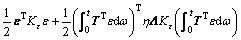 (43)

The derivative of Lyaponov function was as

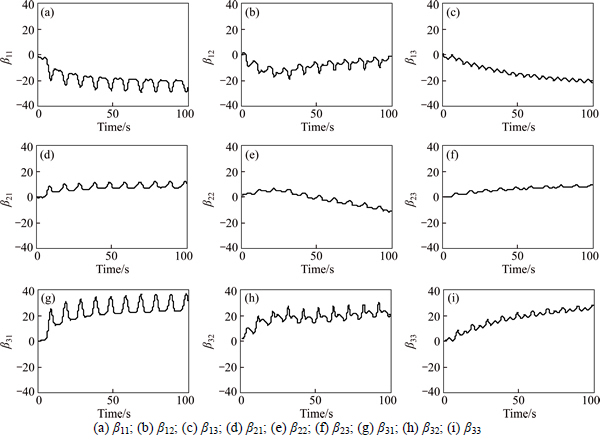
Fig. 5 Parameters estimation of RLSE:

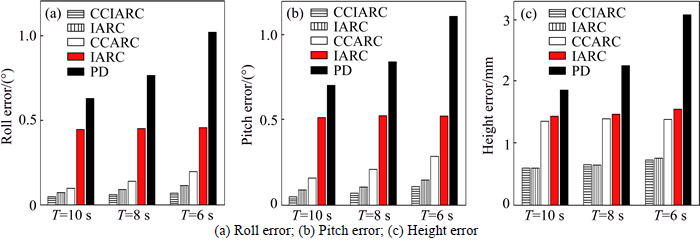
Fig. 6 Trajectory tracking results of various controllers:

Fig. 7 Function of cross-coupling control strategy:

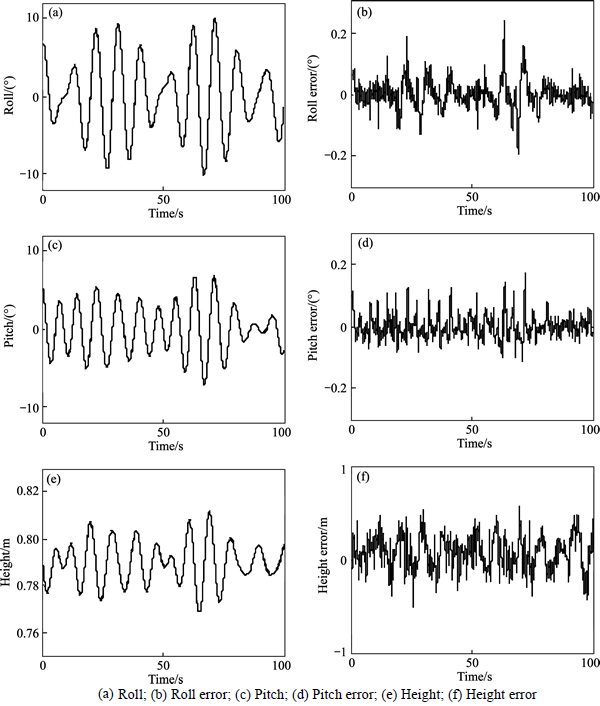
Fig. 8 Trajectory tracking of pseudo random signal^* *|e_M|=[0.2412° 0.1703° 0.5720 mm]^T, e_m=[0.0316° 0.0275° 0.1564 mm]^T:

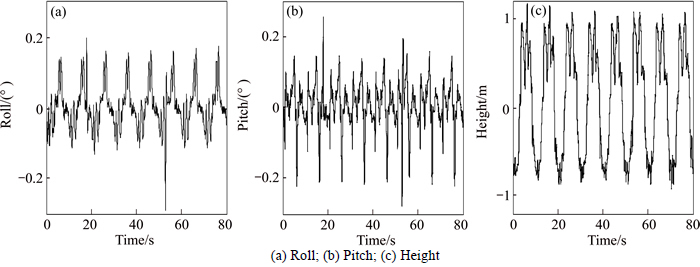
Fig. 9 Robustness test under disturbance:

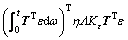                 (44)

The kinematics dynamics model as Eq. (11) was taken into consideration, then the derivative became as

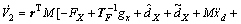
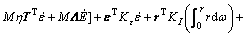
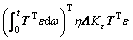                 (45)

The desired force vector was assumed as Eq. (11), and the derivative became as Eq. (46) after compensation of the certain nonlinear model and the adaptive components.

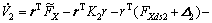
 (46)

If the elements of K_ε were the same and the sum of each line of the coupling matrix T was zero, Eq. (47) could be deduced according to Eq. (13).

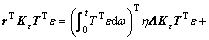
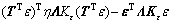            (47)

Then the derivative of the Lyaponov function became as

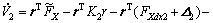
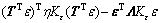             (48)

When 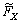equaled zero, according to Eq. (48), the derivative of Lyaponov function satisfied the following inequalities:

 (49)

So, the posture error would converge to a sphere relating to 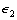under the action of 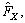which proved the stability of the control system.

Similar as above, a non-positive Lyaponov function was defined as Eq. (50) to prove the convergence of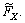

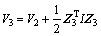                           (50)

Then the derivative of the Lyaponov function was as

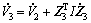
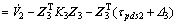            (51)

According to Eq. (23), the derivatives of the Lyaponov function became as

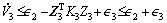                (52)

So, the control error would converge to a sphere related towhich meant the stability of the control system.

References

[1] DAVIS S, TSAGARAKIS N, CANDERLE J, CALDWELL D. Enhanced modelling and performance in braided pneumatic muscle actuators [J]. The International Journal of Robotics Research, 2003, 22(3/4): 213-227.

[2] MINH T V, IJAHJOWIDODO T, RAMON H, BRUSSEL H V. Cascade position control of a single pneumatic artificial muscle-mass system with hysteresis compensation [J]. Mechatronics, 2010, 20(3): 402-414.

[3] ALEXANDER H, JOZEF N M, JAN P, JAN B, KAMIL Z. In tech-model based evolution of a fast hybrid fuzzy adaptive controller for a pneumatic muscle actuator [J]. International Journal of Advanced Robotic Systems, 2012, 9(40): 1-11.

[4] SHI G L, WEI S. Adaptive fuzzy CMAC Position tracking control of parallel platform based on pneumatic artificial muscles [J]. China Journal of Mechanical Engineering, 2012, 23(2): 171-176. (in Chinese)

[5] YANG G, LI B R, FU X. Parallel manipulator driven by pneumatic muscle actuators [J]. China Journal of Mechanical Engineering, 2006, 42(7): 39-45. (in Chinese)

[6] XIE S, JAMWAL P. An iterative fuzzy controller for pneumatic muscle driven rehabilitation robot [J]. Expert Systems with Applications, 2011, 38(7): 8128-8137.

[7] KHOA L, TRUONG D, AHN K. Synchronization controller for a 3-R planar parallel pneumatic artificial muscle (PAM) robot using modified ANFIS algorithm [J]. Mechatronics, 2013, 23(4): 723-741.

[8] ZHAO X W, BIN Z. Design and analysis of a pneumatic muscle driven parallel mechanism for imitating human pelvis [J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2014, 228(4): 723-741.

[9] ZHU X C, TAO G L, YAO B, CAO J. Adaptive robust posture control of parallel manipulator driven by pneumatic muscles with redundancy [J]. IEEE/ASME Transactions on Mechatronics, 2008, 13(4): 441-450.

[10] KOREN Y. Cross-coupled biaxial computer control for manufacturing systems [J]. Journal of Dynamic Systems, Measurement, and Control, 1980, 102: 265-271.

[11] SUN D, WANG C, SHANG W, FENG G. A synchronization approach to trajectory tracking of multiple mobile robots while maintaining time-varying formations [J]. IEEE Transactions on Robotics, 2009, 25(5): 1074-1086.

[12] SUN D. Position synchronization of multiple motion axis with adaptive coupling control [J]. Automatica, 2003, 39(6): 997-1005.

[13] SU Y, SUN D, REN L, JAMES K M. Integration of saturated PI synchronous control and PD feedback for control of parallel manipulators [J]. IEEE Transactions on Robotics, 2006, 22(1): 202-207.

[14] SUN D, LU R, MILLS J K, WANG C. Synchronous tracking control of parallel manipulators using cross-coupling approach [J]. International Journal of Robotics Research, 2006, 25(11): 1137- 1147.

[15] SUN D, FENG G, LAM C M, DONG H. Orientation control of a differential mobile robot through wheel synchronization [J]. IEEE Transactions on Mechathonics, 2005, 10(3): 345-351.

[16] SUN D, SHAO X, FENG G. A model-free cross-coupled control for position synchronization of multi-axis motions: Theory and experiments [J]. IEEE Transactions on Control Systems Technology, 2007, 15(2): 306-314.

[17] SHAN J, LIU H T, NOWOTNY S. Synchronized trajectory-tracking control of multiple 3-DOF experimental helicopters [J]. IEEE Transactions on Control Theory and Applications, 2005, 152(6): 683-692.

[18] XIAO Y, ZHU K Y, LIAW H C. Generalized synchronization control of multi-axis motion systems [J]. Control Engineering Practice, 2005, 13(7): 809-819.

[19] XIAO Y, ZHU K Y. Optimal synchronization control of high-precision motion systems [J]. IEEE Transactions on Industrial Electronics, 2006, 53(4): 1160-1169.

[20] ZHAO D, LI S Y, GAO F. Finite time position synchronized control for parallel manipulators using fast terminal sliding mode [J]. International Journal of Systems Science, 2009, 40(8): 829-843.

[21] ZHAO D, LI S Y, GAO F, ZHU Q. Robust adaptive terminal sliding model-based synchronized position control for multiple motion axes systems [J]. The Institution of Engineering and Technology, 2009, 3(1): 136-150.

[22] ZUO H, TAO G L, ZHU X C. Modeling and enhancement of McKibben pneumatic muscle actuators [J]. Advanced Materials Research, 2012, 591/592/593: 793-796.

[23] TONDU B, LOPEZ P. Modeling and control of McKibben artificial muscle robot actuators [J]. Control Systems, 2000, 20(2): 15-38.

[24] OTTESTAD M, NILSEN N, HANSEN M. Reducing the static friction in hydraulic cylinders by maintaining relative velocity between piston and cylinder [C]// International Conference on Control, Automation and Systems. Jeju Island: IC CAS, 2012: 764-769.

[25] RICHER E, HURMUZLU Y. A high performance pneumatic force actuator system part 1–nonlinear mathematical model [J]. ASME Journal of Dynamic Systems Measurement and Control, 2000, 122(3): 416-425.

[26] BOBROW J, MCDONELL B. Modeling, identification, and control of a pneumatically actuated robot [J]. IEEE Transactions on Robotics and Automation, 1998, 14(5): 732-742.

[27] YAO B, TOMIZUKA M. Adaptive robust control of MIMO nonlinear systems in semi-strict feedback forms [J]. Automatica, 2001, 37(9): 1305-1321.

[28] TAO G L, ZHU X C, YAO B, CAO J. Adaptive robust posture control of a pneumatic muscles driven parallel manipulator with redundancy [C]// Proceedings of the 2007 American Control Conference. New York City, USA: ACC, 2007: 3408-3413.

[29] XU L, YAO B. Adaptive robust precision motion control of linear motors with negligible electrical dynamics: Theory and experiments [J]. IEEE Transactions on Mechatronics, 2001, 6(4): 444-452.

(Edited by DENG Lü-xiang)

Foundation item: Project(51375430) supported by the National Natural Science Foundation of China

Received date: 2014-10-29; Accepted date: 2015-04-20

Corresponding author: TAO Guo-liang, Professor, PhD; Tel +86-571-87951318; E-mail: gltao@zju.edu.cn