
Combining cellular automata and Monte Carlo algorithm to simulate three-dimensional grain growth
WANG Wei1,2, CHEN Ju-hua1, GUO Pei-quan2, ZHAO Ping2 1. School of Mechanical Engineering, Shandong University, Ji’nan 250061, China
2. School of Mechanical Engineering, Ji’nan University, Ji’nan 250022, China
Received 20 April 2006; accepted 30 June 2006
Abstract: A 3-D simulation of grain growth was conducted by utilizing cellular automata (CA) and Monte Carlo (MC) algorithm. In the simulating procedure, the three-dimensional space is divided into a large number of 2-D isometric planes. Then, each of the planes is divided into identical square cells. Finally, the cellular automata and Monte Carlo algorithm are combined together to simulate the grain growth. Through an evolutionary simulation, the recrystallized microstructure, the grain growth rate and the grain size distribution are acceptably predicted. The simulation routine can be used to simulate the real physical-metallurgy processes and to predict quantitative dynamic information of the evolution of microstructure. Further more, the method is also useful for optimization of materials properties by controlling the microstructure evolution.
Key words: three-dimensional simulation; grain growth; cellular automata; Monte Carlo; metallurgy process
1 Introduction Most polycrystalline materials have 3-D microstructure. Due to current technological limits in observation of material microstructure, it is very difficult to study grain growth directly in three-dimensional space by physical experiments. Recently, computer simulations are frequently used to analyze the kinetics of grain growth. It is proved that computer simulation is the most effective tool to explore three-dimensional grain growth evolution. As evolutional processes of gain growth represent in fact a 3-D phenomenon, three-dimensional computer simulations of grain growth are therefore more practical than two-dimensional ones.
The CA and MC algorithms are efficient ways to simulate grain growth process. A great amount of work has been done on simulation of two-dimensional grain growth using CA and MC algorithm as described in Refs. [1-4], but only few studies cover three-dimensional simulations due to complex algorithm and vast computing time[5-8]. In these simulations, the grain growth exponent was lower than the theoretically expected value especially for 2-D simulations. Some three-dimensional simulations were found to have asymptotical value differently[5,6]. Furthermore, the grain size distribution was reported to vary with time in 3-D MC simulations, which could not express the evolution characteristic of real physical process[9].
To simulate grain growth process in three-dimensional space, the most important work is how to make a model of material microstructure. Compared with several similar methods, CA and MC algorithms are the most suitable and effective method. But, as mentioned above, there exist some shortcomings. We combine MC simulation algorithm and CA method together, which will be referred to as CAMC method afterwards, to make the present model as an amended one to simulate grain growth. The results show that the kinetics and topology of grain growth are acceptably predicted.
2 3-D CAMC simulation algorithm
The 3-D CAMC simulation algorithm, which is similar to the simulation procedure in Ref.[2], can be defined as follows:
1) Defining the initial grain structure. As shown in Fig.1, divide the 3-D space of certain volume into a large
number of two-dimensional isometric planes. Each of the planes is then divided into identical square cells. To make the calculation work more accurately, the three-dimensional space is divided into 250×250×250 square cells. To display on a computer screen, each CRT pixel corresponds to a square cell.

Fig.1 Schematics of possible neighborhood
2) Defining the cell neighborhood. For each square cell, its neighborhood is defined by the von Neumann method as elaborated in Fig.1; Each square cell is considered to have six neighbors, four of them are in one plane, the other two are in neighboring planes respectively. The value of each discrete cell is taken from a finite set, which is 1 or 0 in present work, and varies with computing time. The two possible states, 1 and 0, have different meanings in simulation process. The binary variable 1 denotes a recrystallized state, and 0 implies that the square cell is unrecrystallized. The evolution of the grain growth at different times is represented by the value of the individual square cells.
3) Calculating and assigning states to the square cells. Each square cell will be calculated according to the transition equation (1):
 (1)
(1)
where C(i,j,k,t) represents the state of one cell at time t. The function F is the transition rule, which can be defined differently. The evolution of the microstructure is governed by the behavior of individual cells responded to the state of their neighborhood.
4) Calculating the cell transitions and redefining the grain microstructure.
For each square cell, there are six neighboring cells with two states in each one. As cited above, the two states of the cells are 1 and 0, which describe recrystallization and unrecystallization. Therefore, 64 possible evolution states will be got for calculating the cell states.
In present work, GA is utilized to express the state transition. A lookup table for the evolution model is a set of transition rules specifying the possible configuration of the cell’s neighborhood. This lookup table is described as a 64 bit binary string that will be used to represent each of the possible configurations. After each computing time, the string will be changed through evolutionary processes like selection, crossover, and mutation [3]. The state transition is realized by taking a number randomly from the string, and put the number in the cell and calculating the energy differences, which vary from cell to cell.
5) Adoptting the grain-boundary energy defined in terms of lattice site energy as follows:
 (2)
(2)
where Ei is the energy of the lattice site i, J is the grain-boundary energy per area, n is the number of the nearest neighbor lattice site, δ is the Kronecker function, Si and Sj are the orientations of the selected lattice site ‘i’ and its neighboring site ‘j’.
3 Results and discussions
3.1 Grain size distribution
The CAMC simulation process gave a suitable prediction of the grain area fraction, both for recrystallization and unrecrystallization. To calculate the grain size distribution, the variation of grain size should be taken into account. In our work, the grain size was calculated by counting the cell numbers.
As the CAMC computer simulation proceeded, some interesting phenomenon was investigated. When the computing steps were less than 500, the grain size changed a little. But when 1000 steps proceeded, the grain size increased stably as shown in Fig.2. It was definite that when the normal grain growth of the 3-D dimensional system was up to a steady state, the grain numbers per unit volume satisfied with evolutionary theory. The grain numbers in the simulation system reduced progressively, and the time exponent of the grain growth was very close to theoretical value.
Fig.3 shows the grain size distribution of the CAMC simulation. In order to obtain the grain size distribution,
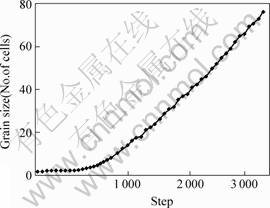
Fig.2 Grain size in cells vs CAMC simulation steps
the grain area had to be measured to some extent in the simulation model. As described above, each grain consisted of several square cells, and the cell numbers were stored in a data file in the computer. Therefore, by computing the cell numbers, the grain area could be liable counted.

Fig.3 Grain size distribution obtained using CAMC simulation
3.2 Microstructure evolution
In the simulation of the grain growth, 5 000 steps were performed. As shown in Fig.4, the evolutionary microstructure in one cross-section of different computing time or step was acceptably predicted. Various microstructure features of normal grain growth observed experimentally were also seen in the microstructure in a specified plane. For instance, the small grains shrank when the large grains grew up, and the angles at most grain corners were 120?. It could also be seen that the normal grain growth was kept stable during the simulation period. No grain coarsening occurred in the long period of evolutionary time. All these observations completely coincided with the previous theory.

Fig.4 Cross-section through simulated microstructure at time of 4 000 steps
Although this algorithm made a perfect prediction of grain growth in microstructure evolutions, the limitations of this algorithm was also obvious. Firstly, it took too much time to compute the whole evolution process due to the complex array of cell definition. Secondly, the computing time or step had no coherent relationship with experimental time, thus the simulation process could not serve easily in virtual experiment. In addition, though the cell definition was three-dimensional, the evolution process was till in cross-section, some features that obtained by the simulation could not support the ones of the three-dimensional space. Therefore, three-dimensional simulation of the microstructure evolution was more appropriate in our future work.
4 Conclusions
A CAMC algorithm model was presented to simulate the normal grain growth. It was flexible and acceptable in predicting the evolution process. It was found that the grain growth rate satisfactorily matched the grain growth theory. While the grain microstructure was obtained from the cross-sections, it was difficult to support the 3-D theory. This three-dimensional simulation model is proposed to be a competitive tool rather than physical experiment. However, the model could be augmented due to the limitations mentioned previously, it will play an important role in the materials science. In the future work, the construction of the lattice would be improved to a perfect one to decrease in great requirement of computer memory and CPU time.
References
[1] CEIGER J, ROOSZ A, BARKOCZY P. Simulation of grain coarsening in two dimensions by cellular-automaton[J]. Acta Materialia, 2001, 49: 623-629.
[2] LIU Y, BAUDIN T, PENELLE R. Simulation of normal grain growth by cellular automata[J]. Scripta Materialia, 1996, 34(11): 1679-1683
[3] DEWRI R, CHAKRABORTI N. Simulating recrystallization through cellular automata and genetic algorithms[J]. Modeling and Simulation in Materials Science and Engineering, 2005, 13(2): 173-178,.
[4] SAITO Y. Monte Carlo simulation of grain boundary precipitation[J]. Materials Science and Engineering A, 1997, 223: 125-133.
[5] LIU Guo-quan, YU Hai-bo, SONG Xiao-yan, QIN Xiang-ge. A new model of three-dimensional grain growth: theory and computer simulation of topology-dependency of individual grain growth rate[J]. Materials & Design, 2001, 22: 33-38.
[6] MEHNERT K, KLIMANEK P. Grain growth in metals with strong textures: three-dimensional Monte Carlo simulations[J]. Computational Materials Science, 1997, 9: 261-266.
[7] KOENRAAD G F, Janssens. Random grid, three-dimensional, space-time coupled cellular automata for the simulation of recrystallization and grain growth [J]. Modeling and Simulation in Materials Science and Engineering, 2003, 11: 157-171.
[8] MARX V, REHER F R, GOTTSTEIN G. Simulation of primary recrystallization using a modified three-dimensional cellular automaton [J]. Acta Materialia, 1999, 47(4): 1219-1230
[9] SONG X Y, LIU G Q. Three-dimensional and cross-sectional characteristics of normal grain growth based on computer simulation[J]. Chinese Journal of Materials Research, 1998, 12(3): 245-250. (in Chinese)
(Editred by CHEN Ai-hua)
Foundation item: Project(Y2002F19) supported by the Science Foundation of Shandong Province; Project (012050107) supported by the Science and Technology Development Project of Shandong Province
Corresponding author: WANG Wei; Tel: 86-531-2765925; E-mail: ujnwangwei@163.com