J. Cent. South Univ. (2016) 23: 1106-1114

DOI: 10.1007/s11771-016-0360-0

Blade pitch control of straight-bladed vertical axis wind turbine

LIANG Ying-bin(梁迎彬)^{1, 2}, ZHANG Li-xun(张立勋)¹, LI Er-xiao(李二肖)³, ZHANG Feng-yue(张凤月)⁴

1. College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China;

2. Beijing Institute of Mechanical Equipment, Beijing 100854, China;

3. Tianjin Pinggao Smart Electric Co. Ltd., Tianjin 300300, China;

4. Department of Technology Center, Great Wall Motor Co. Ltd., Baoding 071000, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: Collective pitch control and individual pitch control algorithms were present for straight-bladed vertical axis wind turbine to improve the self-starting capacity. Comparative analysis of straight-bladed vertical axis wind turbine(SB-VAWT) with or without pitch control was conducted from the aspects of aerodynamic force, flow structure and power coefficient. The computational fluid dynamics (CFD) prediction results show a significant increase in power coefficient for SB-VAWT with pitch control. According to the aerodynamic forces and total torque coefficient obtained at various tip speed ratios (TSRs), the results indicate that the blade pitch method can increase the power output and decrease the deformation of blade; especially, the total torque coefficient of blade pitch control at TSR 1.5 is about 2.5 times larger than that of fixed pitch case. Furthermore, experiment was carried out to verify the feasibility of pitch control methods. The results show that the present collective pitch control and individual pitch control methods can improve the self-starting capacity of SB-VAWT, and the former is much better and its proper operating TSRs ranges from 0.4 to 0.6.

Key words: straight-bladed vertical axis wind turbine; collective pitch control; individual pitch control; self-starting capacity

1 Introduction

As a clean and renewable energy resource, wind energy gains increasing attention in response to climate change and energy crisis [1-2]. With plenty of large-scale commercial wind fields built, the wind power industry had ushered in another wave of vigorous development since late 1970s. With increasing demands for much larger wind farms, the problems of horizontal axis wind turbine (HAWT) are highlighted through the application, some scientists and engineers even claim that HAWTs have reached their maximum size for gravity-induced cyclically reversing stress at root of blades, and large-scale HAWTs might be displaced by vertical axis wind turbine (VAWT) in the future [3]. Meanwhile, there are also increasing demands for larger VAWT for offshore wind farms, which offers distinct advantages over HAWT, including easy installation and maintenance [4-5], stability of blade stress [6], and much stronger adaptive capacity in turbulence and oblique flow [7].

In addition, many researches of SB-VAWTs are carried out to improve its aerodynamic performance and mechanical properties [8-12]. The SB-VAWT with pitch control comes out to be a feasible solution for larger wind farm [13], the self-starting capacity, peak value of power coefficient, tip speed ratio and vibration characteristics of which could be improved by proper pitch control. That is the main reason of SB-VAWT with blade pitch control investigated in this work. The pitch control methods are divided into two groups: passive and active blade pitch control, and the active one is subdivided into collective pitch control and individual pitch control. The majority of investigations of pitch control methods are summarized as follows:

There are two typical applications of passive blade pitch control by PAWSEY [14] and KIRKE [15], the blade pitch angle of which is driven by inertial force and aerodynamic force. A SB-VAWT with electromagnetic pitch control was raised by CAO [16], and the pitch angles were controlled by the aerodynamic force and ectromagnetic force. Due to uncontrollability of passive pitch control method, extensive investigations were implemented for active blade pitch methods, and along with a variety of pitch control mechanism.

Prototypes of SB-VAWT with collective pitch control were designed by COOPER and KENNEDY [17], and ZHANG et al [18]. The motion of blade was half of the rotor but with an opposite rotating direction, leading to a maximum efficiency of 20% at TSR of 0.65. Cam-linkage mechanism was widely used to achieve blade pitch control, the maximum power coefficient of which is about 0.45 [19]. HWANG et al [20] and KIWATA et al [21] put forward linkage mechanisms to achieve cycloidal motion control of blade. The blade pitch angles were determined according to the eccentricity between rotating axis and center of the rotating ring, and the power coefficient of cycloidal rotor is 70% higher than fixed pitch condition [20]. HWANG et al [22] and ZHANG et al [23] proposed SB-VAWTs with individual blade control, and HWANG et al [20] further pointed out that the performance of individual pitch control was 25% higher than that of cycloidal motion. However, it is unfortunately that most of the blade pitch methods are not mature and still need more efforts to be improved.

As mentioned above, a SB-VAWT with individual pitch control mechanism was designed in this work, and along with pitch control methods. Wireless communication was utilized to control rotation of wind turbine and collect information. In addition, numerical simulations were carried out to have a better understanding of mechanical behaviors and flow structure of SB-VAWT. Experimental and numerical investigations were carried out to verify the feasibility of the present pitch control methods.

2 Comparative analysis of S-VAWT

The aim of the present work is to analyze the effects of pitch control methods on overall performance of straight-bladed vertical axis wind turbine. Numerical investigations were carried out by CFD and ANSYS to obtain the mechanical behaviors and flow structure of a three-bladed SB-VAWT. With straight blade employed and the blade-tip vortexes neglected, two-dimensional CFD models of SB-VAWT with blade pitch control and fixed pitch were established. The main geometrical features of the rotor are summarized in Table 1.

Table 1 Main geometrical features of CFD model

2.1 CFD model

In this work, moving mesh and arbitrary sliding interface method were employed for the Darrieus motion. The computational domain was divided into three distinct parts, as shown in Fig. 1.

1) A rectangular far-field zone. It provides a large enough outer flow field, assures the reliability of the numerical analysis and is identified as far-field sub-grid, stationary grid. The total number of grids of the rectangular far-field zone is more than 64000.

Fig. 1 Computational domain and mesh of SB-VAWT with pitch control and fixed pitch:

2) An annular rotating zone. It is identified as rotor sub-grid, operated at a angular velocity ω. The total number of grids of fixed pitch case is 77556, while the number of grids of pitch control case is 65248 without the four blade circles, and that of the grids of each blade circle is about 22338.

3) A circular inner zone. It is identified as inner sub-grid. The total grid number of fixed pitch case is 32000 and it is about 11546 for the pitch control case.

Figure 1(a) shows the main dimensions and boundary conditions of the far-field sub-grid area. The inlet and outlet boundary conditions are placed respectively 6 times of rotor radius upwind and 15 rotor radius times of downwind. The front of domain is defined with boundary condition “velocity inlet”, and the outlet of the domain is defined with the boundary condition “pressure outlet”. Symmetry boundary conditions are employed for two sidewalls, which is 10 times rotor radius in width. Structured mesh is adapted for far-field and sub-grid zones with the purpose of high calculation accuracy and rapid convergence.

The rotor sub-grid is the fluid area simulating the revolution of wind turbine, which is characterized by moving mesh and rotates at the same angular velocity of the turbine. For the case of SB-VAWT with fixed pitch, the blades rotate with the same velocity of the rotor. While for the pitch control case, the relative rotating speed of blades is achieved by user defined function (UDF). It is proved that structured meshes are benefit for controlling the quality of grid, structured meshes are therefore chosen for the rotor sub-grid and the inner sub-grid.

In this thesis, RNG k-ε model with standard wall functions is employed. The incoming flow is 10 m/s and the scale of turbulence of incoming flow uses the default settings. Each of numerical simulation runs until instantaneous torque coefficient values show a deviation of less than 1% compared with the previous period. In addition, residuals convergence criterion for each physical time step is set to 10^-5. An average of about 30 sub-iterations is applied to make the solution converge at each physical time step.

2.2 Mechanical behavior of blade

For two-dimensional CFD simulations, the stress status of a single blade can be simplified as plane force system, the instantaneous force acting on the blade is therefore the net of normal force and tangential force of all the cells, as shown in Eq. (1), as well as a pitch moment M_P relating to rotation center P.

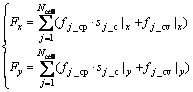              (1)

where f_{j _cp}, f_{j _cv} and s_{j _c} are the normal pressure, viscous force, and area of the jth cell, respectively.

Therefore, the instantaneous tangential force and normal force of a single blade can be derived by

    (2)

where i=0, 1, 2, 3.

Then the tangential force coefficient C_ti and normal force coefficient C_ni are

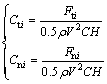                           (3)

where ρ and V are density of air and instantaneous resultant velocity, respectively.

In addition, the pitch moment coefficient C_m is defined as

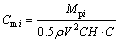                         (4)

Thus, the total driving torque of all blades is

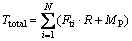                       (5)

The total torque coefficient C_T of SB-VAWT is therefore given by

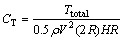                         (6)

Base on Eq. (6), the pitch control methods are obtained, as shown in Fig. 2.

Figure 2(a) shows the pitch control methods under TSR of 1. The pitch control method comes to the collective pitch control by linearization, where the angular velocity of blade is half of the rotor and the initial installation angle of blades are shown in Eq. (7). Figure 2(b) shows the individual pitch control, more details about the present pitch control methods can be found in Ref. [24]. It is worth mentioning that the present individual pitch methods depend upon the aerodynamic parameters of static angle of stall.

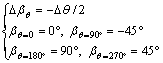                   (7)

Figure 3 shows the normal force coefficient of a single blade at various tip speed ratios (TSRs, R_ts). It can be seen that the majority of normal force coefficient is negative ranging form 0° to 180° and positive ranging form 180° to 360°, indicating that supporting arms (connecting the blade to rotating shaft of wind turbine) suffer from tension at upstream and pressure at downstream. It is also found out that the maximum amplitudes of normal force are located at upwind side (0°≤θ≤90°) of upstream, and increase with TSRs. Moreover, the differences of normal force at various TSRs are much smaller before getting the peak values, while the differences become large after the peaks. It is probably caused by the occurrence of dynamic stall, and a more serious dynamic stall leads to a more bigger loss in normal force.

Fig. 2 Curves of pitch control methods of SB-VAWT:

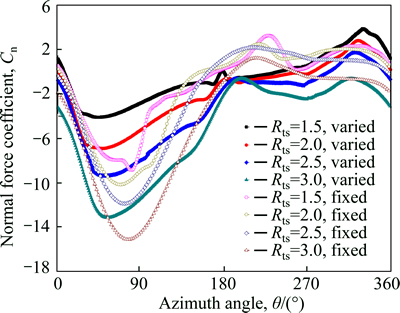
Fig. 3 Curves of normal force coefficient of single blade at various TSRs

In addition, the variation range of normal force coefficient at downstream is much smaller than that of upstream, because the wind speeds of downstream are much lower compared with that of upstream, thus less wind energy can be absorbed at downstream. As shown in Fig. 3, it is obvious that the magnitude of normal force coefficient under pitch control is much smaller than that of fixed pitch, indicating that the pitch control methods are effective to decrease the stress of supporting arms. As can be clearly seen, the regions with negative normal force of pitch control methods become larger, especially at downstream, and this tendency is even more pronounced with the increase of TSRs. The reason for this tendency is that the centrifugal forces become predominant with the decrease of negative pressure between pressure and suction sides caused by changes of blade pitch angle.

Figure 4 shows the tangential force coefficient of a single blade at various TSRs. It can be seen that the maximum tangential forces are located at upstream and the tangential force coefficients at downstream are much lower compared to that of upstream, which is also caused by the much lower wind speeds of downstream. For fixed pitch cases, there are slight increases of peak values of tangential force with increase of TSRs, but the operating regions of TSR to generate higher tangential force are sharply reduced with the decrease of TSR. As can be seen from Fig.4, the operating TSR regions with high tangential force are also the same regardless of the value of TSR. It is concluded that the present pitch control method can enlarge the effective region of TSR.

Fig. 4 Curves of tangential force coefficient of single blade at various TSRs

Form Fig. 4, it is discovered that there are significant fluctuations for the case of R_ts=1.5 under fixed pitch, which is probably due to the serious dynamic stall and secondary vortexes. However, the tangential force coefficient of R_ts=1.5 with pitch control is much better. That is because the in-offset blade pitch angles decrease the angle of attack, avoiding or reducing the possibility and magnitude of dynamic stall. Therefore, it comes to the conclusion that the present pitch control methods are effective to restrain or eliminate the influences of separation and dynamic stall, making the blades in good state to capture wind energy and enlarging the operating region of TSR with high tangential force coefficient.

Figure 5 shows the pitch moment coefficient acting on a single blade. It indicates that the majority of pitch moments at upwind side (-90°<θ<90°) is negative, and the direction of pitch moments are opposite to the rotation direction of rotor. Compared with SB-VAWT with fixed pitch, the pitch moment of pitch control case is much smaller. It should be noted that the pitch moments are resisting moment for fixed pitch case, but they might be useful for blade pitch control, for the direction of pitch moment is consistent with the motion of blade in most region of azimuth angles.

Figure 6 represents the total torque coefficient of SB-VAWT at various TSRs. The torque coefficients of pitch control are much better than that of fixed pitch cases, indicating that the present pitch control methods can improve the overall performance of SB-VAWT. Especially, the torque coefficient of pitch control case at R_ts=1.5 is approximately 2.5 times larger than that of fixed pitch case.

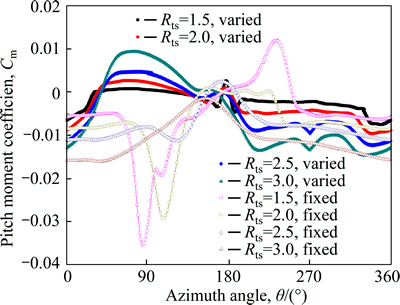
Fig. 5 Curves of pitch moment coefficient relating to blade rotating center at various TSRs

Fig. 6 Curves of torque coefficient of SB-VAWT with or without blade pitch control

In addition, for the pitch control cases, it is found that the torque coefficient of R_ts=1.5 is much larger than those of R_ts=2.0 and R_ts=2.5. It shows that the present pitch control law of R_ts=1.5 has much more satisfying effect, and the pitch methods at other TSRs should be further investigated. From Fig. 6, there is slight increase of torque coefficient when the wind speed is greater than 5 m/s. That is because the effects of Reynolds number on aerodynamic performance become to fall. It also can be seen that the SB-VAWT with blade pitch control will achieve the maximum torque coefficient at a smaller wind speed.

Furthermore, comparative analyses of vibration performance of blade with or without blade pitch control at R_ts=1.5 is carried out. The aluminium alloy blade is simply supported, and only the normal force is considered in the finite element analysis. The aerodynamic forces are simplified as uniformly distributed loads and are located at the axis of rotation of blade; meanwhile the centrifugal force is depicted by the rotating speed of 7.5 rad/s. The maximum deformation and acceleration of blade are shown in Figs. 7 and 8.

Fig. 7 Curves of maximum of total deformation of blade

Figure 7 shows the maximum deformation of blade with TSR of 1.5. It can be seen that the deformation caused by centrifugal force is about 1.75 mm, and the deformation of rotating speed holds dominant position, and the deformation of fixed pitch case has a larger fluctuation range. It is therefore clear to see that both the peak and variation range of maximum deformation of blade pitch control are much smaller than those of fixed pitch case, indicating that the blade pitch method can reduce the deformation of blade and much more wind energy can be translated into mechanical energy. In addition, for the fixed pitch case, the deformations of normal force and centrifugal force at upstream are in the same direction (normal force behaves as tension), while the deformations at downstream are in the opposite direction (normal force behaves as pressure).

Figure 8 shows the directional acceleration (Y axis) of mid-span (z=0.5H) of fixed pitch and pitch control cases. It is obvious that the maximum acceleration at any time is located at the mid-span of blade. It can be seen from Fig. 8 that the directional acceleration (Y axis) of pitch control case is much higher than that of fixed pitch case, which is caused by the frequent changes of blade pitch angle. In order to improve the vibration performance of blade, the present pitch control method should be further investigated.

2.3 Flow structure of SB-VAWT

This section provides a comparative analysis of the flow structure around the wind turbine. Figure 9 shows the vorticity contour and velocity distribution of SB-VAWT with or without blade pitch control. It is found that the distributions of vortices in the wake of wind turbine with blade pitch control are smaller than that of fixed pitch case. For case of fixed blade pitch control, there are much serious loss of wind energy when the incoming flow passes through the rotor, producing plenty of vortexes; however, there are few vortexes for the case of win turbine with blade pitch control, which is the main reason of high efficiency for SB-VAWT with blade pitch control.

Fig. 8 Acceleration of y axis of mid-span of blade over time:

Figure 9 depicts the velocity distribution of wind turbine with or without blade pitch control. It is known that the low velocity zone of wake leads to the increase of pressure. The higher pressure in the wake decreases the mass flow rate through the rotor, having a significant impact on the conversion of wind energy. As can be seen from Figs. 9(c) and (d), the low velocity zone in wake of fixed pitch case is much larger than that of pitch control case. In addition, it is found that the zone with high velocity of fixed blade pitch is larger than that of pitch control case, particularly in the downwind side. It is further pointed out that less wind energy is converted into mechanical energy, the velocity distribution of SB-VAWT with blade pitch control shows the effectivity of blade pitch control methods.

3 Results and discussion

The prototype experiments are performed in a open-circuit wind tunnel, as shown in Fig. 10. The simple wind tunnel consists of four axial flow fans with a diameter of 1 m, a tunnel body with an outlet area of 2 m×2 m, a controller and frequency converter. The outlet speeds of wind tunnel are controlled by the frequency converter. The master controller is mounted upon the spindle of wind turbine and the blade controller is set up at the bottom of the blades; moreover, the master controller and blade controller deliver information by CAN bus. In addition, the collection information of anemometer, anemoscope and master controller are sent to collection system by wireless 485. The slip ring and encoder are located at the lower end of drive shaft, and the azimuth angles recorded by encoder are delivered to the collection system visa RS232. The power supply of the controller and motors are achieved by the slip ring. Control system diagram is shown in Fig. 11.

With the purpose of improving the flow field, a honeycomb is mounted inside of the tunnel body. The uniform flow produced by the simple wind tunnel is measured by using a thermal anemometer, and the test results are shown in Fig. 12. It shows that the distribution of outlet wind speeds produced by the wind tunnel is symmetrical to the center of square cross section of wind tunnel. It is also found that the maximum wind speed is located at the center of wind tunnel, and the wind speeds decrease when it is away from the center. Figure 12 also indicates that the wind speeds around ±0.5 m is much smaller, which is the center of axial flow fans. As the prototype is much bigger than the wind tunnel, the prototype is placed at the center of the square cross the section of wind tunnel, leaving a space of 3 m from the nozzle.

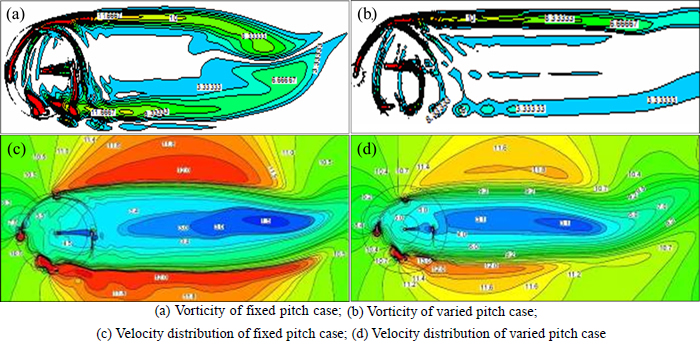
Fig. 9 Vorticity contour and velocity distribution of SB-VAWT with or without blade pitch control:

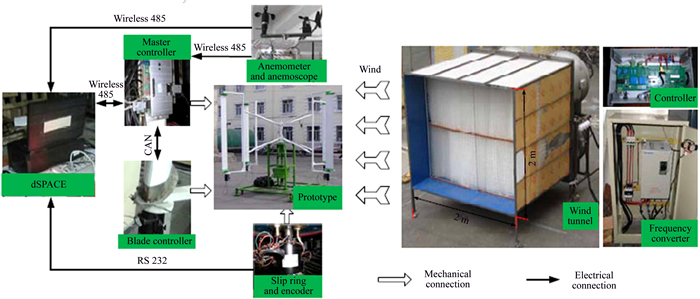
Fig. 10 Experimental apparatus and open-circuit wind tunnel

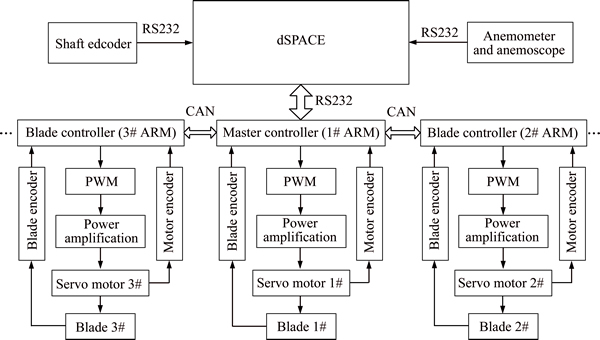
Fig. 11 Diagram of control system of Straight-bladed vertical axis wind turbine

The aim of the present work is to analyze the feasibility of pitch control method, an individual blade pitch mechanism is therefore proposed, where the pitch angle of each blade is controlled by a servo motor, as shown in Fig. 10. According to the present blade pitch mechanism, fixed blade pitch control, collective pitch control and individual pitch control can be achieved by preset blade motion.

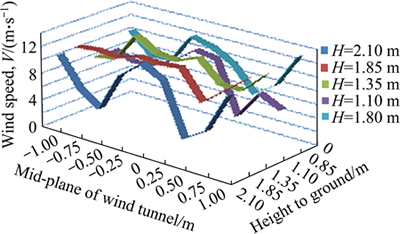
Fig. 12 Test values of wind field produced by wind tunnel

Figure 13 shows the power output of prototype with collective pitch control and individual pitch control. It is found that the prototype could not start with fixed pitch angle, in other words, the power output of prototype with fixed pitch angle is zero. It is obvious that the power increase with the wind speeds, and the power output increases with the decrease of loads. It is concluded that both the collective pitch control and individual pitch control can improve the self-starting capacity, while the collective pitch control is much better than that of R_st=1.5. There are maybe two reasons leading to the condition: 1) the present individual pitch control methods are not desirable, which still needs to be further investigated and improved; 2) the hysterisis error of speed reducer and transmission mechanism make some contributions to the poor performance of the prototype. It is due to the fact that blade rotates in only one direction for the case of collective pitch control, while the blade under individual pitch control is engaged in hunting motion, therefore the hysterisis error makes the blade getting away from the preset pitch angle. Furthermore, both the power output of the collective pitch control and individual pitch control are much lower than that of expected. The relative high rotational inertia and poor wind field could be considered the main responsible for the less efficiency of prototype, which should be further investigated.

Figure 14 shows the power output under collective pitch control. It indicates that the maximum power is located between the TSR range of 0.4 and 0.6 regardless of the wind speeds. It is concluded that the proper operating TSR of the present collective pitch control method is around 0.5.

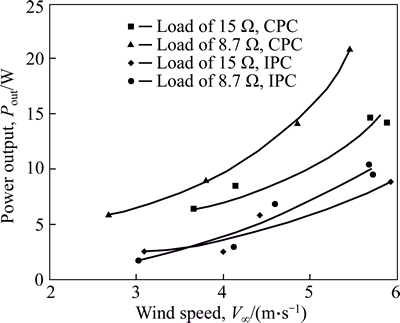
Fig. 13 Power output of prototype with collective pitch control and individual pitch control

Fig. 14 Power output of prototype with collective pitch control under various wind speeds

4 Conclusions

1) The obtained results show that the present pitch control methods can increase the tangential force and enlarge the effective region of TSR; meanwhile it decreases the normal force and pitching moment, which is good for structural design.

2) The total torque coefficient of individual pitch control method at TSR of 1.5 is approximately 2.5 times larger than that of fixed blade pitch case. It is also shown that the distribution of aerodynamic forces and moments of upstream play a significant role in the overall performance of SB-VAWT.

3) It is found that the present collective pitch control and individual pitch control both can improve the self- starting capacity of prototype, and the collective pitch control is much better. The proper operating TSR for the present collective pitch control ranges from 0.4 to 0.6.

References

[1] KLESSMANN C, HELD A, RATHMANN M, RAGWITZ M. Status and perspectives of renewable energy policy and deployment in the European Union—What is needed to reach the 2020 targets? [J]. Energy Policy, 2011, 39(12): 7637-7657.

[2] PRYOR S C, BARTHELMIE R J. Climate change impacts on wind energy: A review [J]. Renewable and Sustainable Energy Reviews, 2010, 14(1): 430-437.

[3] PEACE S. Wind alternatives: Why not vertical axis? [J]. Refocus, 2003, 4(3): 30-33.

[4] ERIKSSON S, BERNHOFF H, LEIJON M. Evaluation of different turbine concepts for wind power [J]. Renewable and Sustainable Energy Reviews, 2008, 12(5): 1419-1434.

[5] ASLAM B M M, HAYAT N, FAROOQ A U, ALI Z, JAMIL S R, HUSSAIN Z. Vertical axis wind turbine—A review of various configurations and design techniques [J]. Renewable and Sustainable Energy Reviews, 2012, 16(4): 1926-1939.

[6] ZAAIJER M. Review of knowledge development for the design of offshore wind energy technology [J]. Wind Energy, 2009, 12(5): 411-430.

[7] SCHEURICH F. Modelling the aerodynamics of vertical-axis wind turbines [D]. Scotland, UK: University of Glasgow, 2011.

[8] FIEDLER A J, TULLIS S. Blade offset and pitch effects on a high solidity vertical axis wind turbine [J]. Wind Engineering, 2009, 33(3): 237-246.

[9] KIRKE B, LAZAUSKAS L. Variable pitch Darrieus water turbines [J]. Journal of Fluid Science and Technology, 2008, 3(3): 430-438.

[10] PARASCHIVOIU I, TRIFU O, SAEED F. H-Darrieus wind turbine with blade pitch control [J]. International Journal of Rotating Machinery, 2009, Article ID 505343.

[11] DOMINY R, LUNT P, BICKERDYKE A, DOMINY J. Self-starting capability of a Darrieus turbine [J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2007, 1: 111-120.

[12] HILL N, DOMINY R, INGRAM G, DOMINY J. Darrieus turbines: The physics of self-starting [J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2009, 223(1): 21-29.

[13] KIRKE B, LAZAUSKAS L. Limitations of fixed pitch Darrieus hydrokinetic turbines and the challenge of variable pitch [J]. Renewable Energy, 2011, 36(3): 893-897.

[14] PAWSEY N C K. Development and evaluation of passive variable- pitch vertical axis wind turbines [D]. Australia: University of New South Wales, 2002.

[15] KIRKE B K. Evaluation of self-starting vertical axis wind turbines for stand-alone applications [D]. Australia: Griffith University, 1998.

[16] CAO L P. Mechanism and method about blade pitch control of vertical axis wind turbine by using magnetic and wind forces: China, 201010188237.9 [P]. 2013-04-17.

[17] COOPER P, KENNEDY O C. Development and analysis of a novel vertical axis wind turbine [C]// The 42nd Annual Conference of the Australian and New Zealand Solar Energy Society. Perth, Australia: Australian and New Zealand Solar Energy Society (ANZSES), 2004: 1-9.

[18] ZHANG L X, ZHANG S, WANG K, LIANG Y B. Study on synchronous variable pitch vertical axis wind turbine [C]// 2011 Asia-Pacific Power and Energy Engineering Conference. Wuhan, China: IEEE, 2011: 1-5.

[19] GRYLLS W, DALE B, SARRE P E. A theoretical and experimental investigation into the variable pitch vertical axis wind turbine [C]// The 2nd international symposium on wind energy systems. Amsterdam, the Netherlands, 1978: 122-138.

[20] HWANG I S, LEE Y H, KIM S J. Optimization of cycloidal water turbine and the performance improvement by individual blade control [J]. Applied Energy, 2009, 86(9): 1532-1540.

[21] KIWATA T, YAMADA T, KITA T, TAKATA S, KOMATSU N, KIMURA S. Performance of a vertical axis wind turbine with variable-pitch straight blades utilizing a linkage mechanism [J]. Journal of Environment and Engineering, 2010, 5(1): 213-225.

[22] HWANG I S, MIN S Y, JEONG I O, LEE Y H, KIM S J. Efficiency improvement of a new vertical axis wind turbine by individual active control of blade motion [C]// Smart Structures and Materials 2006: Smart Structures and Integrated Systems, 2006: 316-323.

[23] ZHANG Li-xun, ZHANG Song, WANG Xiao-yu, JIAO Qi-fei, LIANG Ying-bin, YANG Yong. Pitching laws of smart variable- pitch vertical axis wind turbine [J]. Acta Energiae Solaris Sinica, 2013, 34(8): 1427-1433.

[24] ZHANG Li-xun, LIANG Ying-bin, LIU Xiao-hong, GUO Jian. Effect of blade pitch angle on aerodynamic performance of straight- bladed vertical axis wind turbine [J]. Journal of Central South University, 2014, 21(4): 1417-1427.

(Edited by FANG Jing-hua)

Foundation item: Project(E201216) supported by Heilongjiang Provincial Natural Science Foundation, China

Received date: 2015-03-17; Accepted date: 2015-07-22

Corresponding author: ZHANG Li-xun, Professor, PhD;Tel: +86-451-82569486;E-mail: zli_xun@163.com