DOI: 10.11817/j.issn.1672-7207.2017.04.031

基于起伏形态特征的节理岩石峰值剪切强度准则

曹平¹，龙龙^{1, 2}，范文臣^{1, 2}，范祥¹，曹日红¹

(1. 中南大学 资源与安全工程学院，湖南 长沙，410083；

2. 湖南科技大学 煤矿安全开采技术湖南省重点实验室，湖南 湘潭，411201)

摘要：运用RYL-600剪切流变仪对不同法向应力下的人工花岗岩试件进行多次剪切试验，得到不同法向应力下的剪切应力-剪切位移曲线，并运用TALYSURF CLI 2000对剪切前后节理面进行形貌扫描，得到节理面3维形貌图。通过试验方法得到节理剪切强度与形貌的关系。在试验结果的基础上，考虑起伏形态参数节理面整体轮廓角加权平均值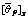对剪切强度的影响，并对Barton准则进行修正，将由修正的Barton准则计算的剪切强度与试验结果进行对比。研究结果表明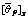：随着剪切次数增加而减小；修正的Barton准则计算结果与试验结果较吻合，能较好地预测节理剪切强度。

关键词：岩石力学；节理形貌；峰值强度；轮廓线平均角

中图分类号：TD21        文献标志码：A         文章编号：1672-7207(2017)04-1081-07

Peak shear strength criterion for rock joints based on undulating characteristics

CAO Ping¹, LONG Long^{1, 2}, FAN Wenchen^{1, 2}, FAN Xiang¹, CAO Rihong¹

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines,

Hunan University of Science and Technology, Xiangtan 411201, China)

Abstract: Shear tests of artificial granite joints under different normal stresses were conducted with RYL-600,and the curves of shear stress versus shear displacement under different normal stresses were obtained. The 3D scanning images were obtained before and after each shear tests under different normal stresses with TALYSURF CLI 2000.Relationships between morphology of jointed rock surfaces and shear strength were studied experimentally. Based on the experiment, the undulating characteristics of joint surfaces were analyzed. Barton criterion modification was made by considering undulating characteristic 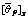. Comparison among the experimental data, Barton criterion and modified Barton criterion were made to evaluate the accuracy of the modified criterion. The results show that the average of the mean profile angles 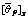decreases with the increase of the times of shear tests. The shear strength values calculated by the modified Barton criterion agree well with the testing results and the shear strength of jointed rock can be predicated by the new criterion.

Key words: rock mechanics; joint morphology; peak shear strength; mean profile angle

岩体是由结构面纵横切割而具有一定结构的多裂隙体，结构面的存在对岩体的变形和破坏起着控制作用^[1]。国内外学者对节理岩体力学性质的研究主要是在考虑节理面形貌参数下建立峰值剪切强度准则^[2-4]，节理面表面形态影响节理面的接触状态和剪切摩擦作用，从而影响节理剪切强度。PATTON等^[5]通过研究锯齿状节理，在光滑节理剪切强度的基础上提出了考虑起伏角的剪切强度公式；吴启月等^[6]建立J_RC-J_CS模型和Mohr-Coulomb模型参数之间关系，并分析了J_RC-J_CS模型对剪切强度的影响；JAEGER^[7]提出负指数剪切强度公式，该公式实际上是对PATTON^[5]双直线剪切强度公式的光滑处理，与PATTON^[5]剪胀公式并无本质区别；LADANYI等^[8]从节理剪切的机理出发，建立了考虑摩擦力、剪胀性、黏结性和岩桥特性的剪切强度公式。BARTON等^[9-10]等通过大量试验，提出表征节理面粗糙特性的节理面粗糙度系数J_RC，并由此建立了J_RC-J_CS的剪切强度准则，但由于对J_RC取值较主观，且二维剖面线难以全面表征节理的三维形貌特征，因此，所计算的强度与实验值差距较大；ZHAO^[11-12]提出节理吻合系数(J_MC)概念，在BARTON等^[9-10]的J_RC-J_CS强度准则基础上，提出考虑节理表面粗糙度和吻合度的J_RC-J_MC强度准则。节理面的力学性质与节理面的形态有关，而节理面的形态通过节理面的起伏形态和粗糙度这2个因素来描述。上述强度准则中，BARTON等^[9]的强度准则考虑节理面的粗糙度的影响，而缺少对节理面起伏形态的研究；PATTON^[5]考虑了起伏角的影响，但没考虑节理面粗糙度的影响。GRASSELLI等^[13]通过恒定法向荷载直剪试验，建立考虑三维形貌参数的抗剪强度公式；孙辅庭等^[14]引入分形粗糙度、分形粗糙度维数和分布参数来表征岩石节理形貌，建立了不同形貌特征下峰值剪切强度准则。需要注意的是，GRASSELLI等^[13]的研究需要精度较高的仪器获得形貌参数。研究表明^[15]，分形理论不能准确反映非匀质性和各向异性节理断面特征，因此，孙辅庭等^[14]建立的剪切强度公式也有待完善。综上分析，节理岩体抗剪强度准则的建立需要综合考虑节理面的粗糙度和起伏度特征。为此，本文尝试在BARTON强度准则的基础上，通过考虑反映节理面起伏形态的特征参数整体轮廓平均角的加权平均值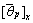，建立含有节理面的粗糙特性以及起伏形态的剪切强度公式。首先，通过巴西劈裂试验方法获取新鲜人工节理试件，对试件进行室内剪切试验获取节理剪切曲线和峰值剪切强度，并运用TALYSURF CLI 2000激光扫描仪对每次剪切前后节理面形貌进行扫描；其次，建立节理面峰值剪切强度与形貌参数的关系；最后，将修正的强度准则与BARTON强度准则进行对比。修正的强度准则能较好地反映节理面粗糙特性和起伏形态，具有较明确的物理意义，并且修正剪切强度公式中参数均可通过统计学计算得到，能较准确地反映节理岩体剪切力学特性。

1  试验概况

1.1  剪切试件制备

本文选用长×宽×高为70 mm×70 mm×70 mm的3组干燥花岗岩试件，在进行巴西劈裂获得新鲜耦合节理试件，图中箭头指向表示试件的剪切方向，见图1。直径为50 mm、高为100 mm的标准圆柱状完整花岗岩试件的基本力学参数见表1。

图1  花岗岩节理试件

Fig. 1  Photos of jointed granite specimens

表1  花岗岩试样力学参数

Table 1  Mechanical parameters of granite specimens

1.2  试验设备

1.2.1  RYL-600岩石剪切流变仪

剪切试验采用RYL-600岩石剪切流变仪。该仪器主要由松下伺服电机及控制系统、德国DOLI测控系统、法向主机、横向主机、横向剪切框架组成，最大横向剪力达200 kN，横向位移加载速率为0.001~50 mm/min，主要应用于岩石流变、单轴压缩以及结构面剪切试验。本次试验采用常法向荷载剪切，通过计算控制系统记录剪力、剪切位移、法向力等参数。

1.2.2  TALYSURF CLI 2000形貌扫描仪

TALYSURF CLI 2000是由英国Taylor Hobson公司研制的三维非接触式激光扫描仪，主要由激光扫描测量装置、控制单元、计算机、数据分析软件TalyMap 5.0组成。该仪器最大扫描范围为200 mm×200 mm× 200 mm，扫描精度可达0.05 μm。试件放置在可沿x和y方向移动的操纵台上，通过控制激光探头扫描位置确定扫描范围。当激光探头沿x轴移动时，仪器利用三角光学原理测量其距表面的距离，当测到某一条扫描线末端时，则在y方向步进一个步长(0.05 μm)，开始新x方向扫描。

1.3  剪切试验与形貌测试

对3组岩石试件进行分组编号，分别在常法向压应力1，2和5 MPa下进行剪切试验(试验时室温为25~27 ℃)，每个法向应力下均剪切4次，随之得出剪应力-剪位移曲线。试验时，先加法向荷载到设定值并保证上、下节理面充分耦合，后通过位移控制施加切向荷载，剪切速率为0.3 mm/min。当剪位移达到6 mm时停止试验，以确保达到剪切残余阶段。

剪切试验前后，利用形貌扫描仪对节理面的形貌进行激光扫描，设定扫描间距为0.1 mm，扫描速度为20 mm/s。形貌仪扫描的结果保存为.SUR格式文件，利用软件TalyMap 5.0对.SUR文件对形貌轮廓均方根偏差、形貌偏态系数、形貌峰态系数等微观形貌高度特征参数进行分析，也可对形貌轮廓面积比、形貌坡度均方根以及形貌展开界面面积比率等微观形貌纹理特征参数进行分析。

2  试验结果分析

当法向应力为1，2和5 MPa时的剪应力-剪切位移曲线见图2(其中，n为剪切次数)。法向应力为2 MPa时4次剪切前后节理表面三维形貌见图3。为了直观地反映节理面剪切前后的变化，试验采用最小二乘面作为形貌测试的基准面。为了便于观察，图3中的节理面高度均放大1.3倍，并用颜色来反映节理面的高度。

由图2可知：随着剪切次数n增加，节理试件的抗剪强度逐渐减小，初次剪切出现峰值后，曲线逐渐下降并达到残余阶段；多次剪切试验后，峰值在剪应力-剪位移曲线图中显现越来越不明显。

由图3可知：初次剪切后，存在较大凸起体处的节理面被剪断，剪切应力-位移曲线出现峰值；随着剪切次数增加，节理面白色区域呈现增多趋势，表明节理面较高区域逐渐被磨损剪平，导致在第2，3和4次剪切未出现明显的峰值而直接到达残余阶段；当法向应力较大时，节理面会随着剪切进行磨损程度增大，此时，节理面的起伏形态控制着剪切应力，说明节理面峰值剪切强度与形貌参数和法向应力有直接关系。

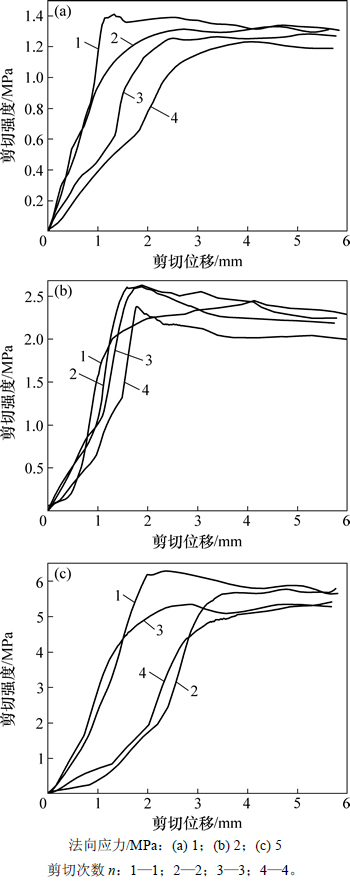
图2  不同法向应力下4次剪切的剪切应力-位移曲线

Fig. 2  Shear stress-shear displacement curves under different normal stresses for 1 to 4 shear times

3  含起伏形态特征的剪切强度公式

3.1  J_RC取值分析

节理剪切强度准则的建立需考虑剪切强度与节理面粗糙度参数以及剪胀角之间的关系。BARTON^[10]提出10条标准剖面线，通过选取有代表性的轮廓剖面线与之比较，得出节理粗糙度系数J_RC，由下式计算峰值剪切强度τ_p：

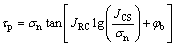        (1)

式中：J_RC取值为0~20；φ_b为节理面基本摩擦角；J_CS为节理壁面抗压强度；σ_n为试验中施加的法向应力。

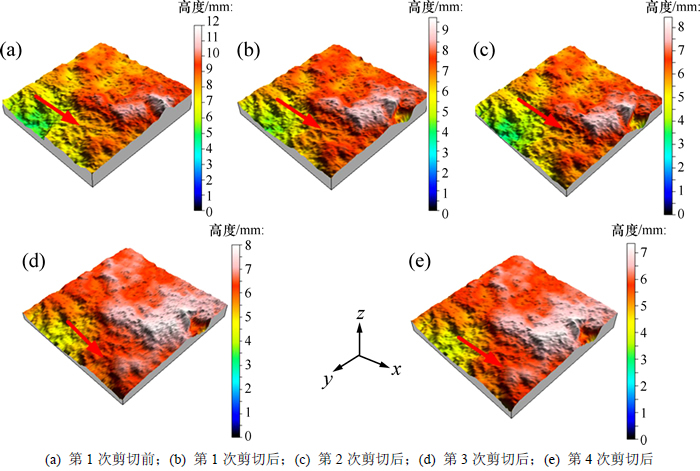
图3  2 MPa法向应力下，节理面经过1~4次剪切后的三维形貌

Fig. 3  Micro-morphologies of upper surfaces of rock joints under 2 MPa normal stresses after 1 to 4 times shear

BARTON剪切准则中对J_RC的确定缺乏定量描述，并且具有较大主观性。事实上，在表面形态特征研究中，表面形态的高度可视为一系列随机变量，运用统计学参数能较好地描述形貌特征^[1]。TSE等^[16]用结构函数S_F来估算J_RC，故选用文献[16]中的计算式：

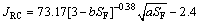       (2)

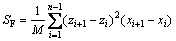        (3)

式中：a和b为粗糙度幂参数，并由文献[16]中介绍的方法确定；M为节理面轮廓线长度；z_i为对应于x_i时的轮廓线高度；n为轮廓高度计算点总数。

本次试验中，选取法向应力为1，2和5 MPa的新鲜节理面试件，沿剪切方向(x方向)等间距提取10条轮廓线，等间距选取轮廓线坐标，间距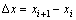，为2.5 mm(同一位置上、下节理面各10条)，见图4。

由式(1)~(3)分别计算不同法向应力下4次剪切后的S_F，J_RC以及Barton剪切强度，其中S_F和J_RC由组成节理面的各轮廓线加权平均得到，计算结果见表2和表3。

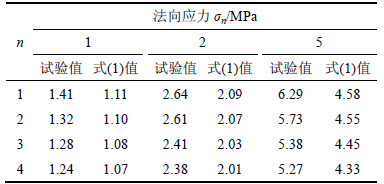
由表3可见：BARTON剪切强度公式计算的峰值剪切强度比试验值低。BARTON等^[9]认为，凸起体的剪断与剪胀性和法向应力有关，而实际上，由于大部分天然岩石节理的表面形貌中包含起伏度分量和粗糙度分量，这2部分对节理剪切性质的影响不同。在剪切过程中，由节理面形貌特征引起的剪胀效应应该考虑起伏度和粗糙度的影响，因此，本文作者在BARTON强度准则的基础上，通过考虑表征表面形貌起伏特征的整体轮廓平均角的加权平均值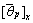，建立含有节理面的粗糙特性以及起伏形态的剪切强度公式。

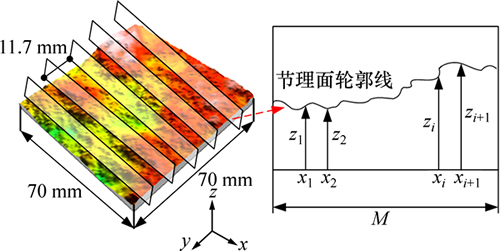
图4  节理面轮廓线提取方式

Fig. 4  Method of profile extraction on joint surface

表2  4次剪切下节理面的S_F与J_RC

Table 2  Values of S_F and J_RC of joints for 1 to 4 shears

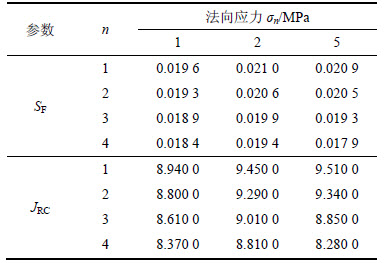
表3  剪切强度试验值与式(1)计算值比较

Table 3  Peak shear strengths of experimental results and calculated values by Eq. (1)     MPa

3.2  修正节理峰值剪切强度公式

HOMAND等^[17]提出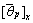，用于表示沿剪切方向(x方向)且垂直于节理面的剖面中各处微元斜率平均值对应的角度，文献[2]将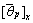定义为节理面整体轮廓平均角的加权平均值。本文沿剪切方向(x方向)计算整体轮廓平均角的加权平均值且所取的轮廓线名义长度相等，计算式为

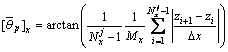     (4)

式中：j为轮廓编号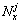；为第j条轮廓线沿x方向总测点数；M_x为沿x方向轮廓线总数。

据文献[18]，随着剪切次数增加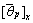，减小。由式(2)和(3)可知：相邻节理表面高度差△z会减小，J_RC也会减小。对不同法向应力下J_RC和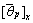进行分析，计算结果见图5。

由图5可知：J_RC和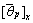变化趋势一致，均减小；在第3次剪切后，节理面整体轮廓角加权平均值变化较小，主要是由于前2次剪切后，大部分凸起体被剪断，在更大的法向应力下，节理面的磨损程度增大，节理面起伏较大区域被剪平，导致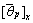变化不明显。故认为峰值抗剪强度与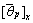有关。

本文在Barton经验剪切强度式基础上提出考虑起伏形态及粗糙度2个因素的新节理峰值抗剪强度公式：

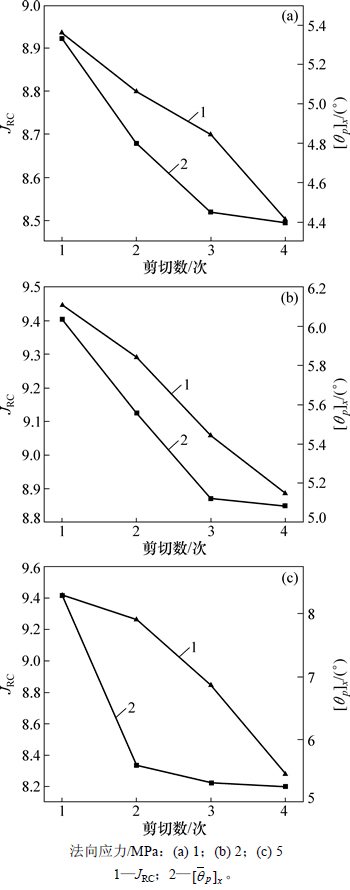
图5  不同法向应力下4次剪切时的J_RC和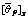变化曲线

Fig. 5  Curves of J_RC and 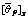under different normal stresses for four shear times

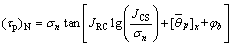    (5)

式中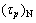：为新的剪切强度；J_CS为单轴抗压强度(未风化花岗岩)；φ_b取值为30°^[1]。

令式(5)中剪胀角i为

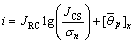           (6)

剪胀角i为包含了节理形貌中粗糙特性和起伏特性的参数，且均可通过量化计算得到，克服了BARTON准则中由于取值的主观性而造成的偏差。

修正后的剪切强度准则是基于节理面粗糙度和节理面起伏特性而建立的，公式形式简单，只需要进行基本的力学试验和形貌测量，即可获得相关参数进行剪切强度预测。表4所示为由式(4)和(5)计算的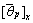与修正的剪切强度计算值。

表4  4次剪切下节理面的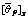与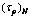

Table 4 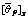and 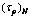of joints for 1 to 4 shears

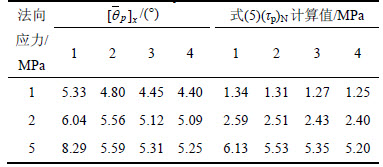
采用修正剪切强度计算值与Barton公式计算值进行比较，见图6。

由图6可知：由BARTON准则计算的强度与试验值相比存在较大偏差，表明在三维节理表面下仅仅考虑节理面轮廓线的粗糙度系数不能准确地描述节理面形态。

3.3  误差分析

利用平均相对误差^[19]来评价新的剪切强度、BARTON准则值与试验值的偏差，计算式为

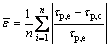           (7)

式中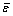：为平均相对误差；n为剪切强度试验次数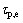；为剪切强度试验值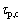；为计算值。计算式(1)和式(5)在1，2和5 MPa下多次剪切后抗剪强度的平均相对误差，计算结果见表5。

由表5可知：式(1)在高法向应力下的试验值与计算值偏差最大；式(5)考虑了节理面起伏形态特征和粗糙度特征，计算的剪切强度与试验值的平均偏差明显较低，适合于预测节理抗剪强度。

由上述分析可知：修正的强度准则是对BARTON 准则的优化，当节理面光滑时，修正的强度公式则变形为PATTON剪胀公式^[5]。在考虑节理面起伏特性的修正强度准则能更好地估算节理岩体峰值抗剪强度，且计算误差更小。

表5  平均相对误差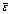分析结果

Table 5  Average relative error 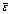analysis result     %

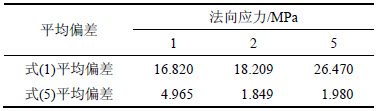
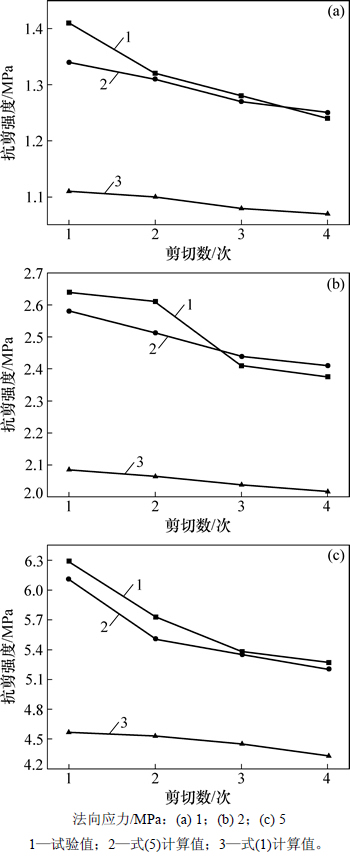
图6  节理剪切强度试验值与计算值的比较

Fig. 6  Comparison between experimental and calculated peak shear strengths of rock joints

4  结论

1) 采用统计学参数计算得出的节理面J_RC比用对比法得到的J_RC更客观。节理面的整体轮廓角的加权平均值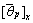和J_RC随着剪切次数的增加而减小。

2) 提出将整体表面的轮廓角的加权平均值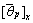作为反映节理面起伏形态的参数，在BARTON剪切强度准则上进行改进，修正强度公式参数均可通过节理面轮廓线计算得到。

3) 对比分析了2种峰值剪切强度准则。新强度准则同时考虑了节理面的粗糙度J_RC和起伏形态参数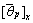，与BARTON剪切强度公式所得峰值剪切强度相比更接近试验值。

参考文献：

[1] 夏才初, 孙宗颀. 工程岩体节理力学[M]. 上海: 同济大学出版社, 2002: 1-22.

XIA Caichu, SUN Zongqi. Engineering rock mass joint mechanics[M]. Shanghai: Tongji University Press, 2002: 1-22.

[2] SON B K, LEE Y K, LEE C I. Elasto-plastic simulation of a direct shear test on rough rock joints[J]. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(3): 354-359.

[3] 夏才初, 宋英龙, 唐志成. 反复直剪试验节理强度与粗糙度变化的研究[J]. 中南大学学报(自然科学版), 2012, 43(9): 3589-3594.

XIA Caichu, SONG Yinglong, TANG Zhicheng, et al. Shear strength and morphology characteristic evolution of joint surface under cyclic loads[J]. Journal of Central South University (Science and Technology), 2012, 43(9): 3589-3594.

[4] 王刚, 黄娜, 蒋宇静, 等. 一种新型粗糙节理面随机强度模型及其应用[J]. 岩土力学, 2014, 35(2): 497-503.

WANG Gang, HUANG Na, JIANG Yujing. New stochastic strength model of rough rock joint surfaces and its application[J]. Rock and Soil Mechanics, 2014, 35(2): 497-503.

[5] PATTON F D. Multiple modes of shear failure in rock[C]//Proceeding of the First Congress of International Society of Rock Mechanics. Lisbon, Spain. 1966: 509-513.

[6] 吴启红, 徐青, 雍军, 等. 节理面JRC-JCS非线性准则的数值计算方法[J]. 中南大学学报(自然科学版), 2013, 44(9): 3829-3833.

WU Qiyue, XU Qing, YONG Jun. Numerical embedding in FLAC3D of JRC-JCS model of joint plane[J]. Journal of Central South University (Science and Technology), 2013, 44(9): 3829-3833.

[7] JAEGER J C. Friction of rocks and stability of rock slopes[J]. Geotechnique, 1971, 21(2): 97-134.

[8] LADANYI B, ARCHAMBAULT G. Simulation of shear behavior of a jointed rock mass[C]//The 11th US Symposium on Rock Mechanics (USRMS). California, America: American Rock Mechanics Association, 1970: 105-125.

[9] BARTON N, CHOUBEY V. The shear strength of rock joints in theory and practice[J]. Rock mechanics and Rock Engineering, 1977, 10(1/2): 1-54.

[10] BARTON N. Review of a new shear-strength criterion for rock joints[J]. Engineering Geology, 1973, 7(4): 287-332.

[11] ZHAO Jian. Joint surface matching and shear strength. Part A: joint matching coefficient(JMC)[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(2): 173-178.

[12] 赵坚. 岩石节理剪切强度的 JRC-JMC 新模型[J]. 岩石力学与工程学报, 1998, 17(4): 349-357.

ZHAO Jian. A new JRC-JMC shear strength criterion for rock joint[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(4): 349-357.

[13] GRASSELLI G, EGGER P. Constitutive law for the shear strength of rock joints based on three-dimensional surface parameters[J]. International Journal of Rock Mechanics and Mining Sciences, 2003, 40(1): 25-40.

[14] 孙辅庭, 佘成学, 万利台, 等. 基于三维形貌特征的岩石节理峰值剪切强度准则研究[J]. 岩土工程学报, 2014, 36(3): 529-536.

SUN Fucheng, SHE Chengxue, WAN Litai, et al. Peak shear strength criterion for rock joints based on three-dimensional morphology characteristics[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 529-536.

[15] OUTER A D, KAASHOEK J F. HACK HRGK Difficulties with using continuous fractal theory for discontinuity surfaces[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1995, 32(1): 3-9.

[16] TSE R, CRUDEN D M. Estimating joint roughness coefficients[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1979, 16(5): 303-307.

[17] HOMAND F, BELEM T, SOULEY M. Friction and degradation of rock joint surfaces under shear loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(10): 973-999.

[18] 曹平, 范祥, 蒲成志, 等. 节理剪切试验及其表面形貌特征变化分析[J]. 岩石力学与工程学报, 2011, 30(3): 480-485.

CAO Ping, FAN Xiang, PU Chengzhi, et al. Shear test of joint and analysis of morphology characteristic evolution of joint surface[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(3): 480-485.

[19] 唐志成, 刘泉声, 刘小燕. 节理的剪切力学性质与含三维形貌参数的剪切强度准则比较研究[J]. 岩土工程学报, 2014, 36(5): 873-879.

TANG Zhicheng, LIU Quansheng, LIU Xiaoyan, et al. Shear behavior of rock joints and comparative study on shear strength criteria with three-dimensional morphology parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 36(5): 873-879.

(编辑  陈灿华)

收稿日期：2016-05-10；修回日期：2016-07-12

基金项目(Foundation item)：国家自然科学基金资助项目(51274249)；煤矿安全开采技术湖南省重点实验室开放基金资助项目(201406)(Project (51274249) supported by the National Natural Science Foundation of China; Project (201406) supported by Hunan Key Laboratory of Coal Resources and Safe Mining Open-end funds)

通信作者：曹平，教授，博士生导师，从事岩石力学与工程应用研究；E-mail：pcao_csu@sina.com