基坑应变软化的桩锚支护数值计算

刘自由

(湖南城市学院 土木工程学院，湖南 益阳，413000)

摘要：通过理论分析，建立相应基坑应变软化模型，并对桩锚支护过程中的基坑稳定情况和桩锚结构响应进行数值模拟。研究结果表明：利用FLAC^3D建立的应变软化模型，能够较好地反映土的特性；基坑安全系数随锚杆长度的增大而呈线性增大；若锚杆的长度较短，则基坑的稳定性受到锚杆倾角的影响较小；锚固力沿杆体方向逐渐减小，最大值出现在锚头位置；随着锚杆长度的增大，锚固力最大值往杆体内移动，并沿杆体呈先增大后减小的趋势；支护桩主要承受压力作用，随着锚杆长度的增大，支护桩所承受的压力逐渐减小；锚杆倾角增大导致支护桩轴向压力逐渐增大。

关键词：基坑；桩；锚杆；稳定性；数值模拟

中图分类号：TU457         文献标志码：A         文章编号：1672-7207(2012)07-2833-05

Numerical calculation for pile-cable reinforcement in strain softening foundation pit

liu zi-you

(School of Civil Engineering, Hunan University of City, Yiyang 413000, China)

Abstract: By theoretical analysis, the strain softening foundation pit model was founded, and the stability situation of foundation pit reinforced by pile-cable and its response were numerically simulated. The results show that the strain soften model built by FLAC^3D can reflect the characteristic of soil mass; the factor of safety of foundation pit increases with the increase of bolt length; the bolt inclination has little effect on the safety factor of foundation pit, and the maximum anchoring force exists at the bolt head. With the increase of the bolt length, the maximum bolt force moves to the middle of bolt shaft, which causes the anchoring force to first increase and then decrease. The reinforcement pile mainly resists the compression in the axial direction. With the increase of bolt length, the compression along the pile shaft decreases gradually. With the increase of the bolt inclination, the axial compression along pile increases gradually.

Key words: foundation pit; pile; bolt; stability; numerical simulation

基坑开挖往往导致土体应力迅速释放，并产生一定的位移，影响基坑的稳定性，因此，需进行一定支护^[1-2]。桩锚结构作为一种基坑支护结构，自产生以来，在国内外得到广泛应用^[3-5]，它能合理利用土体自承能力，发挥桩锚与土体的黏结作用，具有造价低廉、施工迅捷等优点。目前，桩锚支护基坑稳定，一般采用简化模型，但由于桩锚结构与土体相互作用过程涉及复杂的力学机理，若采用简化的力学模型分析往往不能反映基坑和桩锚相互作用的实际情况，不能合理地有针对性地进行设计处理，留下一定工程隐患，或者由于设计保守，造成工程浪费。近年来，随着计算机技术和各种数值模拟方法的不断发展，基于数值计算结果的岩土工程设计研究正逐渐显现其强大优势和重要作用^[6]。一些研究者研究了边坡在锚杆单独支护形式下的稳定性以及锚杆支护参数的影响^[7-8]；而对于基坑在桩锚联合支护情况下，支护参数对基坑稳定性的影响以及桩锚耦合效应方面的研究较少。此外，以往的数值分析一般采用Mohr-Coulomb理想弹塑性模型描述土体的强度特征，而较少采用更加符合岩土体材料强度特征的应变软化模型^[1]。为此，本文作者以某深基坑为背景，建立符合实际情况的应变软化模型，并以该模型为基础，分析基坑在桩锚支护过程中的变形破坏情况，探讨支护参数对基坑稳定性的影响。

1  应变软化模型

应变软化模型是Mohr-Coulomb模型的一种特殊形式，当材料发生塑性应变后，黏结力、内摩擦角、剪胀角和拉伸强度将发生变化。在主应力空间σ₁-σ₃平面内，因为剪切失效，根据摩尔-库仑屈服准则，包络线f^s=0可用下式表示：

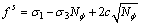            (1)

式中：c为黏结力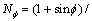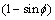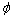；；为内摩擦角。

由拉伸失效准则，其包络线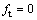可以用下式表示：

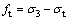                  (2)

式中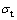：为抗拉强度，其最大值为

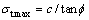                 (3)

岩土体的剪切和拉伸塑性流动法则根据和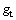来确定。岩土体的非关联流动法则根据确定，

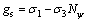               (4)

其中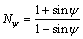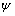：；为剪胀角；函数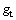表示岩土体的相关联流动法则，

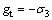                  (5)

若岩土体单元的三维应力状态不超过应力空间中的屈服面，则岩土体单元处于弹性状态，不需要进行塑性修正。但若岩土体单元应力状态达到屈服条件，则根据相应的塑性流动法则，对应力进行修正，使应力状态处于屈服面上。

2  数值计算

2.1  计算模型

某基坑计算模型如图1所示，其中，基坑深为10 m，分5步开挖，每步2 m；模型整体长为60 m，高为30 m，宽度取锚杆横向布置间距为2 m。基坑模型底部固定约束，两侧法向约束，上部为自由边界。为分析锚杆倾角和长度对于基坑稳定性和支护桩受力的影响，从上到下布设5层锚杆，将锚杆倾角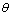变化范围为[0°, 45°]，锚杆长度L变化范围为2~32 m；采用强度折减法^[9-10]计算基坑的安全系数。为了真实地模拟基坑的开挖变形过程，将计算过程分为2步：地应力平衡和基坑开挖计算。土体计算参数如下：容重为19.0 kN/m³，弹性模量为20.0 MPa，泊松比为0.3，黏结力为50.0 kPa，内摩擦角为22.0°；锚杆计算参数如下：钻孔直径为100.0 mm，弹性模量为200.0 GPa，泊松比为0.25，内摩擦角为25.0°，黏结刚度为1.0 GN/m²，黏结力为15.0 kPa；支护桩的计算参数如下：弹性模量为25.0 GPa，泊松比为0.33，法向黏结力为0.175 GN/m，法向刚度为1.0 GN/m²，切向黏结力为0.175 MN/m，切向摩擦角为31.0°，黏结刚度为1.0 GN/m²。根据土的性质、固结情况等，土体可以呈现应变软化或者应变硬化，针对以上各种不同状态，需要对其选择不同的模型，对于黏土或结构性黏土以及紧密砂土等土体，它们在受力屈服后，会呈现出受力软化的特征。黏土是本文所研究基坑的土体，根据FLAC^3D[9]，在选择土质软化模型参数上，应该选择应变软化模型来描述该基坑；土体相应的c_p和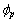在岩土发生塑性变形后与原始c_i和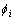的对应关系应该为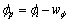：；。其中：w_c为黏结力的变化因子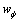；为内摩擦角的变化因子。w_c和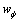与塑性应变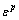的关系见表1。

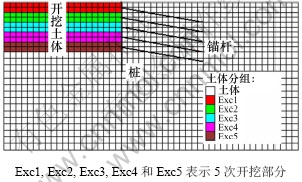
图1  数值计算模型

Fig.1  Numerical calculation model

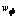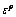表1  w_c和与塑性应变的关系

Table 1  Relationship among w_c, 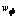 and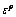

2.2  支护参数对于基坑稳定性的影响

通过强度折减法^[9-10]计算得到基坑安全系数F随锚杆长度L的变化情况，结果如图2所示。从图2可见：基坑安全系数随锚杆长度的增加而增大；但当锚杆倾角为30°时，规律并不相同，此时，锚杆存在一有效锚固长度L_eff，若L＞L_eff，则基坑安全系数将不随锚杆长度的增加而增大，在本算例中，L_eff=16 m；而对于其他锚杆倾角在计算长度范围内并不存在有效锚固长度，与锚杆单独加固情况下的结果不同^[11]。这是由于在桩锚加固过程中，不仅锚杆发挥了锚固效用，而且桩的加固能力也起到了支护作用，从而使有效锚固长度大大增加；此外，基坑安全系数F随锚杆长度L呈线性变化，可采用线性方程对二者的关系进行拟合，所得结果见表2。从表2可见：拟合相关系数较高；随着θ的增大，拟合曲线的斜率B呈先增大后减小的趋势；当θ=20°时，B取最大值0.064，说明此时基坑的安全系数受锚杆长度的影响最大，因此，锚杆倾角θ=20°为最优锚固角。这是由于当锚杆倾角为20°时，锚杆与基坑的潜在滑动面的夹角最接近90°，从而能产生最大的锚固力。

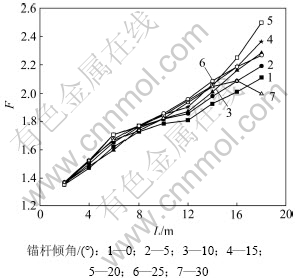
图2  基坑的安全系数F随锚杆长度L的变化情况

Fig.2  Relationship between factor of safety F of foundation pit and bolt length

表2  基坑的安全系数F随锚杆长度L的变化情况

Table 2  Factor of safety F of foundation pit with change of bolt length

基坑安全系数随锚杆倾角的变化情况见图3，基坑的安全系数F随锚杆长度的变化情况见表2。从图3可见：当锚杆倾角θ变化时，基坑安全系数随之发生的相应变化。由图3可见：曲线在锚杆长度处于区间[2, 4] m时起伏较小，说明θ在锚杆长度比较小时，其变化对基坑的安全系数影响并不大；当L为16和18 m时，基坑安全系数F随θ的增大呈现的趋势为先增大后减小，当θ=20°时基坑的安全系数达到极大值，说明此时基坑受到该锚杆倾角的影响最大。因此，可将此时的锚杆倾角θ=20°作为最优锚固角，该结果与上述分析结果一致。

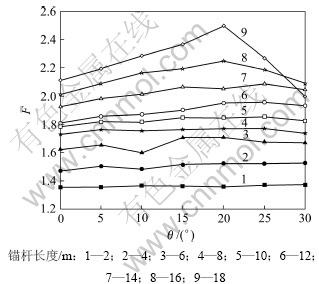
图3  基坑安全系数F随锚杆倾角θ的变化情况

Fig.3  Relationship between factor of safety of foundation pit and bolt inclination

2.3  桩锚耦合效应分析

由于θ＝20°为本算例中的最优锚固角，因此，选取θ＝20°，改变锚杆长度L，以第1层锚杆为例，得到锚杆轴力分布情况，如图4所示。从图4可以看出：当锚杆长度较小时，锚固力沿锚杆体方向逐渐减小，锚固力最大值均出现在基坑壁表面锚头位置；随着锚杆长度的增大，锚固力最大值逐渐往杆体内部移动(如表2所示)，使锚固力沿锚杆分布呈先增大后减小的趋势。可见：锚杆轴力分布并不均匀，若采用以往设计中锚杆轴力均匀分布的假设，则与实际不符。

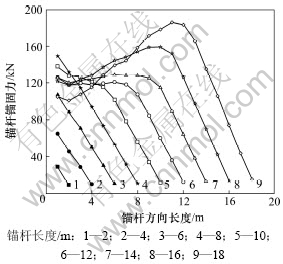
图4  锚固力随锚杆长度的变化情况

Fig.4  Relationship between anchoring force and bolt length

表3  轴力最大位置与锚杆长度的关系

Table 3  Relationship between location of maximum axial force and bolt length

选取锚杆长度L=16 m和倾角θ=20°为例，得到各层锚杆的锚固力沿锚杆体的分布情况，如图5所示。从图5可见：第1层锚杆锚固力沿杆体呈先增大后减小的趋势，最大值位于距锚头大约11.0 m位置的杆体上；第2层锚杆锚固力沿杆体呈逐渐减小的趋势；而其他几层锚杆的锚固力沿锚杆长度方向呈现先减小后增大再减小的趋势，并且这些层锚杆的锚固力最大值均出现在锚头位置。

以锚杆长度L=16 m情况为例，第1层锚杆锚固力随锚杆倾角的变化情况如图6所示。从图6可以看出：随着锚杆倾角的增大，锚杆提供的总体锚固力也逐渐增大；当锚杆倾角较小如θ=0°时，锚固力沿杆体呈先减小后增大再减小的趋势，这是由于此时锚杆无法贯穿滑动面，锚头与土体间的相对位移在整个锚杆体中为最大；而锚杆倾角θ=5°~10°时，锚固力沿杆体方向呈不断减小的趋势；当锚杆倾角较大如θ=15°~30°时，锚固力呈现先增大后减小的趋势。这是由于此时锚杆能够贯穿滑动面，在贯穿位置，锚杆与土体的相对位移在整个锚杆体中为最大，从而产生最大的锚固力。

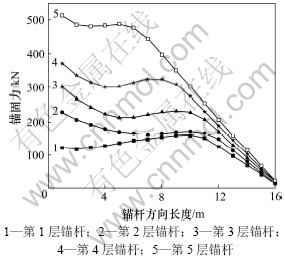
图5  锚杆锚固力的分布情况

Fig.5  Distribution of anchor force of bolt along anchoring direction

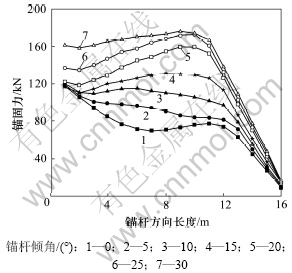
图6  不同锚杆倾角下锚固力沿锚杆长度方向的变化情况

Fig.6  Variation of anchoring force of bolt along anchoring direction under different bolt inclinations

以锚杆倾角θ=15°为例，分析支护桩轴力随锚杆长度的变化情况，探讨支护结构之间的耦合效应，结果如图7所示。从图7可见：支护桩主要承受压力作用。以L=10 m为例，探讨支护桩轴力随锚杆倾角的变化情况，如图8的示。从图8可见：当锚杆倾角θ不同时，支护桩轴向主要承受压力，压力最大的位置位于桩体10 m左右处；随着θ的增大，支护桩承受的轴力也不断增大。这是由于锚杆所提供的锚固力逐渐增大，导致在支护桩体上的反作用力也逐渐增大。

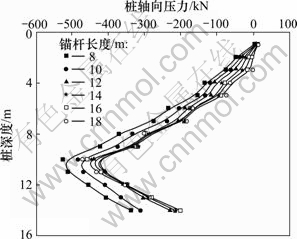
图7  不同锚杆长度下桩轴力的变化情况

Fig.7  Variation of axial force of pile under different lenghts

图8  不同锚杆倾角下桩轴力的变化情况

Fig.8  Variation of axial force of pile under different bolt inclinations

3  结论

(1) 基坑安全系数随锚杆长度呈线性变化，可采用线性方程对二者的关系进行拟合，拟合相关系数较高。当锚杆长度较小时，改变锚杆倾角对基坑安全系数的影响不大；当锚杆长度较大时，基坑安全系数随θ的增大呈先增大后减小的趋势。

(2) 锚杆轴力沿杆体分布并不均匀。随着锚杆倾角的增大，锚杆提供的总体锚固力也逐渐增大。支护桩主要承受压力作用，并且压力的分布沿桩身呈现先增大后减小的趋势；随着锚杆长度的增加，支护桩所承受的压力逐渐减小。

参考文献：

[1] 卢敦华, 王星华. 基于应变软化模型的深基坑土钉加固分析[J]. 解放军理工大学学报, 2009, 10(1): 61-66.
LU Dun-hua, WANG Xing-hua. Soil nail reinforcement in deep foundation pit based on strain softening model[J]. Journal of PLA University of Science and Technology, 2009, 10(1): 61-66.

[2] 屠毓敏, 阮长青, 赵向前, 等. 温州大剧院深基坑支护技术[J]. 岩土工程学报, 2006, 28(1): 59-62.
TU Yu-min, RUAN Chang-qing, ZHAO Xiang-qian, et al. Protecting technique for deep excavation of Wenzhon Grand Theater[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(1): 59-62.

[3] 孙铁成, 张明聚, 杨茜. 深基坑复合土钉支护模型试验研究[J]. 岩石力学与工程学报, 2004, 23(15): 2385-2392.
SUN Tie-cheng, ZHANG Ming-ju, YANG Qian. Modeling study on composite soil nailing for deep excavation[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(15): 2385-2392.

[4] 杨林德, 李象范, 钟正雄. 复合型土钉墙的非线性有限元分析[J]. 岩土工程学报, 2001, 23(2): 149-152.
YANG Lin-de, LI Xiang-fan, ZHONG Zheng-xiong. The nonlinear analysis of FEM on composite soil-nailed retaining wall[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(2): 149-152.

[5] 彭孔曙, 胡敏云, 沈维维. 复合土钉墙设计计算方法研究[J]. 浙江工业大学学报, 2006, 34(1): 15-19.
PENG Kong-shu, HU Min-yun, SHEN Wei-wei. Research on the calculating method for the whole stability of composite soil-nailed wall[J]. Journal of Zhejiang University of Technology, 2006, 34(1): 15-19.

[6] 林杭, 曹平. 锚杆长度对边坡稳定性影响的数值分析[J]. 岩土工程学报, 2009, 31(3): 470-474.
LIN Hang, CAO Ping. Numerical analysis for the effect of cable length to the stability of slope[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(3): 470-474.

[7] 彭文祥, 赵明华, 袁海平, 等. 基于拉格朗日差分法的全长注浆锚杆支护参数优化[J]. 中南大学学报: 自然科学版, 2006, 37(5): 1002-1007.
PENG Wen-xiang, ZHAO Ming-hua, YUAN Hai-ping, et al. Parameters analysis of grouted bolts by Lagrangian difference method[J]. Journal of Central South University: Science and Technology, 2006, 37(5): 1002-1007.

[8] 苏霞, 李仲奎. 锚杆拉拔力影响因素的数值试验研究[J]. 工程力学, 2006, 23(2): 97-102.
SU Xia, LI Zhong-kui. Numerical study of the influence factors of anchorage under tension[J]. Engineering Mechanics, 2006, 23(2): 97-102.

[9] 林杭, 曹平, 赵延林, 等. 强度折减法在Hoek-Brown准则中的应用[J]. 中南大学学报: 自然科学版, 2007, 38(6): 1219-1224.
LIN Hang, CAO Ping, ZHAO Yan-lin, et al. The application of strength reduction method in Hoek-Brown criterion[J]. Journal of Central South University: Science and Technology, 2007, 38(6): 1219-1224.

[10] 赵尚毅, 郑颖人, 张玉芳. 有限元强度折减法中边坡失稳的判据探讨[J]. 岩土力学, 2005, 26(2): 332-336.
ZHAO Shang-yi, ZHENG Ying-ren, ZHANG Yu-fang. Study on slope failure criterion in strength reduction finite element method[J]. Rock and Soil Mechanics, 2005, 26(2): 333-336.

(编辑 陈灿华)

收稿日期：2011-08-11；修回日期：2011-10-24

基金项目：国家自然科学基金资助项目(50774093)

通信作者：刘自由(1968-)，男，湖南桃江人，硕士，副教授，从事建筑材料力学性能研究；电话：0737-4628297；E-mail: liuziyoucsu@126.com