J. Cent. South Univ. Technol. (2008) 15(s1): 475-478

DOI: 10.1007/s11771-008-403-2

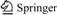
Experimental study on rheological deformation and stress properties of limestone

TANG Ming-ming (唐明明), WANG Zhi-yin (王芝银)

(Beijing Key Laboratory of Urban Oil and Gas Distribution Technology, China University of Petroleum, Beijing 102249, China)

Abstract: The systematic experiment regarding the general uniaxial compression test and the creep deformations of the typical limestones from the surrounding rock of the highway tunnels were made. The relationship between the axial stress and the delayed deformation steady value was obtained from the creep tests under low loading stresses. By the least square method, the parameters of Nishihara creep model were calculated from the creep curves. The results indicate that the strain change always lags behind the increase of stress, and the long-term strength of the limestone is about 80.6% of the stress at the volumetric strain reversal which is obtained from the conventional uniaxial compression test.

Key words: creep experiment; long-term strength; stress at volumetric strain reversal; limestone

1 Introduction

The underground rock structures occasionally show large delayed displacements that can lead to failure and the time-dependent deformation of rocks have a significant impact on the stability of rock structures. This phenomenon illustrates the long-term viscous behaviour of rocks. In tunneling, if the time-dependent deformation is not considered, the ground may continue to deform with time, and furthermore it may cause failure after a tunnel excavation and a support installation^[1-2].

In long-term loading tests, the time-dependent deformation behavior of rocks has a corresponding relationship with the complete stress-strain curve obtained from the general uniaxial compression test. During a long-term constant stress test, the creep curve can be divided into three parts: 1) Primary creep phase, also known as transient creep, during which the strain rate decreases and the deformation stabilizes over a long time; 2) Secondary creep phase, or steady-state creep, during which the strain rate remains constant; 3) Tertiary creep phase, during which the strain rate increases because of the occurrence of progressive rock damage. However, previous results obtained from tests on other rocks show that a stress threshold should exist. When the loading stress is lower than the threshold, only the primary creep would develop and the visco-plastic deformation would stabilize over a long time^[2-4]. This stress threshold is always assumed to be the same as σ_cd, which is defined as the stress level where the volumetric strain reversal occurs. Some researchers obtained a good correspondence between the long-term strength and the stress threshold for granite^[5]. However, this comparison is not true for some rocks such as sandstone^[2]. The concept of limit curve was proposed by Be’rest et al, and it is defined by the points reached at the end of creep. For low levels of loading stress, the delayed deformation stabilizes asymptotically to the value corresponding to the deformation reached at the same level of stress on the limit curve^[2-3].

In this paper, several specimens of limestone from the surrounding rock of Xi-Kang Highway tunnels were chosen as the study objects. A general uniaxial compression test and six creep tests were carried out. Then, based on the tests, the time-dependent deformation of the limestone was characterized.

2 Test equipment and sample preparation

In order to obtain the stress threshold and the steady state creep rate of the limestone, one sample was tested for the conventional uniaxial compression test and six samples were tested for the long-term loading test. Each sample was prepared with radio of length to diameter ratio 2?1. The drilling tool decides the diameter of the samples: 49.2-50.1 mm. In order to control the divergence of the mechanical behaviours of different samples, all samples for tests were drilled from one rock with a volume of about 0.05 m³.

In creep tests, the amplitude of delayed strain depends on the test conditions. So the room temperature was controlled and maintained at 27.1 ℃. The stress was applied by a servo-controlled system with a capacity of 2 MN in axial direction, and 80 MPa in radial direction. The servo-controlled system controlled the stress variation to be less than 0.05 MPa, about 0.2% of the applied stress. The data were recorded with a sampling period set to 10 s for conventional unaxial compression, and 1 min for long-term creep tests when the creep time is less than 20 h and 1 h for long-term creep tests when the creep time is longer than 20 h.

3 Results analysis

3.1. Conventional uniaxial compression test

The curves of the uniaxial compression test are shown in Fig.1, where ε₁ is axial strain, ε₂ is radical strain, and ε_v is volume strain with the relation of ε_v=ε₁+ 2ε₂. Under uniaxial compression, this stress—strain curve of the limestone can be divided into three stages:

1) Crack closure, when the stress is 0-8 MPa and the axial strain is 0-0.05%;

2) Linear elasticity, when the stress is 8-93 MPa and the axial strain is 0.05%-0.2%;

3) Crack growth, when the stress is less than 93 MPa and the axial strain is less than 0.2%. σ_cd, which is defined as the stress level where the volumetric strain reversal occurs, indicating that the dilation exceeds the elastic compression of the rock. σ_cd depends on the loading rate. Form Fig.1 it can be seen that, when the loading rate is 300 N/s, σ_cd is about 93 MPa and the compression strength is about 108 MPa.

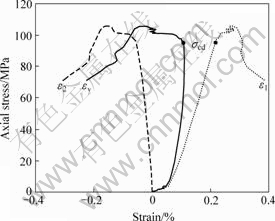
Fig.1 Curves of conventional uniaxial compression test

3.2 Creep test

In order to evaluate the stress threshold, six samples were tested in uniaxial creep tests with the constant compression stresses of 40 MPa (43% σ_cd), 50 MPa (53.8% σ_cd), 60 MPa (64.5% σ_cd), 70 MPa (75.3% σ_cd), 80 MPa (86.0% σ_cd) and 90 MPa (96.8% σ_cd), respectively, according to the conventional unaxial compression test. Each sample was tested for more than 100 h, and the creep curves are shown in Fg.2.

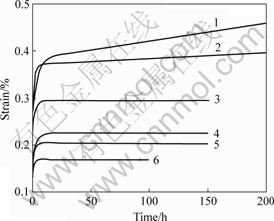
Fig.2 Curves of creep tests Axial stress/MPa: 1—90; 2—80; 3—70; 4—60; 5—50; 6—40

From Fig.2 it can be seen that, when the loading stress is less than 70 MPa, the strain rate decreases and the delayed deformation stabilizes over a long period, and when the loading stress is more than 80 MPa, the strain rate decreases and then keeps at a constant value more than 0. From Figs.3-4, it can be seen that when the loading stress is 80 MPa, the creep rate of the secondary creep stage is about 1.2×10^-6 h^-1, and when the loading stress is 90 MPa, the creep rate of the secondary creep stage is about 3.8×10^-6 h^-1. This means that the creep rate of the secondary creep stage increases with the increase of loading stress. Furthermore, the durations of the first creep stage are 3.6, 6.3, 13.0, 8.9, 14.6 and 19.8 h when the loading stresses are 40, 50, 60, 70, 80 and 90 MPa, respectively. The relation between the first creep stage durations and the loading stresses is shown in Fig.5. The general relation is that the duration of the first creep

Fig.3 Curve of creep rate when the axial stress is 80 MPa and the steady creep rate is 1.2×10^-6

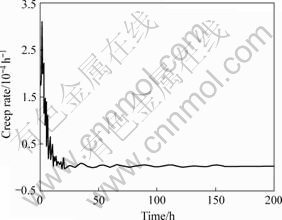
Fig.4 Curve of creep rate when the axial stress is 90 MPa and the steady creep rate is 3.8×10^-6

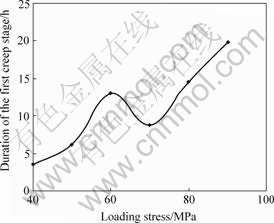
Fig.5 Relation between durations of the first creep stage and loading stress

stage increases with the increase of loading stress. The inflexions appear when the loading stresses are 60 MPa and 70 MPa, and such inflexions may be caused by the discreteness of rocks.

It can be obtained from the test that the stress threshold is more than 70 MPa and less than 80 MPa, so the stress threshold can be chosen as the average value of 75 MPa, which is not equal to σ_cd but only 80.6% of the maximum volume strain contraction σ_cd. This phenomenon can be explained as follows: The strain changes always lags behind the increase of the stress. Let it be supposed that, in the conventional uniaxial test, the loading stress is applied at a very low strain rate which is slow enough to sustain the development of viscoplastic strains in real time. This means the strain and the stress change synchronously. Therefore, when the loading stress is slightly less than σ_cd, the growth, coalescence and interaction of cracks begin to be unstable, and when the loading reaches σ_cd, the growth, coalescence and interaction of cracks are unstable, and the volumetric strain reversal occurs. So, the long-term strength of rock is always lower than the stress threshold.

It is possible to draw the approximate limit curve^[2] of the limestone according to the creep curves under low stresses. The relation between the limit curve and the stress—strain curve is shown in Fig.6. When the loading stress is less than the long-term strength, the relation between the steady creep deformations of the first creep phase and the loading stresses can be formulated as follows:

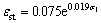                            (1)

where  ε_st is axial steady creep strain and σ₁ is constant axial stress. In Fig.7, the dotted line is the fitting curve and the solid line is connected by the actual creep data points.

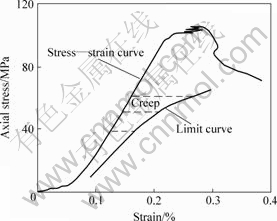
Fig.6 Relation between limit curve and stress—strain curve

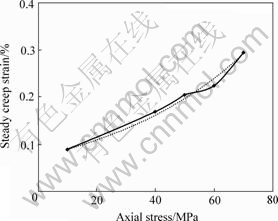
Fig.7 Relation between steady creep strain and axial stress

4 Creep model and back calculation of parameters

According to Fig.2, the characters of the creep curves are in accord with those of Nishihara creep model. The constitutive law of Nishihara model (shown in Fig.8) is combined by a visco-elastic model and a visco-plastic model. If σ＜σ_s1, it becomes the H-K model, and if σ≥σ_s1, its behavior is similar to the Burger’s model^[6]:

σ＜σ_s1,

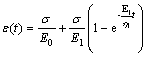                     (2)

σ≥σ_s1,

            (3)

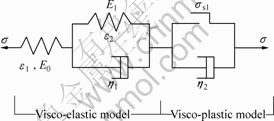
Fig.8 Structure of Nishihara creep model

According to the creep curves, the parameters of Nishihara model which are calculated by the least square mtethod are shown in Table 1.

Table 1 Parameters calculated from the curves

It can be deduced from Table1 that the divergence of the parameter E₀ is not clear while the divergences of the parameters E₁ and η₁ are remarkable. The general trend is that the parameter E₁ decreases with the increase of axial stress, while the paramete η₁ increases with the increase of axial stress. The divergence of the parameter η₂ will not be defined because only two values are obtained. The relations between the parameters and the axial stresses are shown in Fig.9.

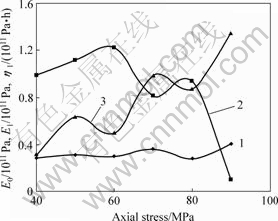
Fig.9 Relations between the parameters and the axial stresses:  1—E₀; 2—E₁; 3—η₁

5 Conclusions

1) Experimental data related the general uniaxial compression test and the creep deformations of a typical limestone are obtained. The long-term strength of the limestone is about 80.6% of the stress at the volumetric strain reversal.

2) The relation between the axial stress and the delayed deformation steady value is obtained.

3) The creep parameters of the limestone which are known from one rock are not constant, but change nonlinearly with the stress level.

References

[1] TSAI L S, HSIEH Y M, WENG M C. Time-dependent deformation behaviors of weak sandstones[J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45(2): 144-154.

[2] FABRE G, PELLET F. Creep and time-dependent damage in argillaceous rocks[J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(6): 950-960.

[3] FUJII Y, KIYAMA T, ISHIJIMA Y, KODAMA J. Circumferential strain behavior during creep tests of brittle rocks[J]. International Journal of Rock Mechanics & Mining Sciences, 1999, 36(3): 323-337.

[4] BIENIASWSKI Z T. Mechanism of brittle fracture of rock. Part I: theory of the fracture process[J]. J International Rock Mech Min Sci Geomech Abstr, 1967, 4(4): 395-406.

[5] MARTIN C D, CHANDLER N A. The progressive fracture of lac du Bonnet granite[J]. J International Rock Mech Min Sci Geomech Abstr, 1994, 31(6): 643-659.

[6] WANG Zhi-yin, LI Yun-peng. Rheological theory and numerical simulation of rock mass[M]. Beijing: Science Press, 2008. (in Chinese)

(Edited by CHEN Can-hua)

Foundation item: Project(50774090) supported by the National Natural Science Foundation of China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: TANG Ming-ming, Doctor candidate; Tel: +86-10-89733926; E-mail: tmm_sugar@126.com