DOI：10.19476/j.ysxb.1004.0609.2018.12.03

基于GTN模型的镁合金异形件颗粒介质成形

曹秒艳¹，左苗苗¹，王  鹏¹，郝海滨²，赵长财²，李建超²

(1. 燕山大学 国家冷轧板带装备及工艺工程技术研究中心，秦皇岛 066004;

2. 燕山大学 先进锻压成形技术与科学教育部重点实验室，秦皇岛 066004)

摘  要：对AZ31B镁合金复杂截面零件固体颗粒介质成形过程进行研究。结合镁合金热态单向拉伸试验和有限元逆向法，确定预测热态下镁合金成形极限的Gurson-Tvergaard-Needleman(GTN)模型损伤参数。以镁合金异形件为研究对象，基于镁合金GTN损伤模型，采用有限元软件ABAQUS模拟该异形件的成形过程，分析不同工艺参数对工件壁厚和孔洞体积分数的影响，确定了该异形件的最佳成形工艺参数。设计了镁合金异形件固体颗粒介质成形模具并展开了相关试验，试验结果与基于GTN损伤模型的仿真结果基本吻合，并基于最佳模拟参数获得了合格的零件。

关键词：镁合金；异形件；GTN模型；颗粒介质

文章编号：1004-0609(2018)-12-2413-09　　     中图分类号：TG386.43　　     文献标志码：A

金属塑性成形中主要发生韧性断裂，韧性断裂过程可以分为3个阶段：首先，在晶界、第二相粒子与母体材料的界面等位置形成微空洞；其次，微空洞不断长大；最后，当孔洞体积分数到达临界值时，孔洞开始发生聚合，形成宏观裂纹，材料的承载能量下降，然后断裂^[1]。基于主应变，最大拉伸力或变形能量密度的传统的断裂准则没有考虑材料断裂的实际发展过程，一个准则只适用于一种特定的变形方式^[2]。铝、镁合金等轻金属材料在高温下失效一般是由空洞引起的，而其力学性能也主要是由空洞程度决定的。基于细观损伤力学的GTN损伤模型能够很好地从微观角度解释材料损伤的产生和演化过程， 而且该模型考虑了应力三轴度对韧性断裂的影响^[3]。由于压应力可以减缓或停滞材料损伤扩展，所以材料的塑性变形能力随着应力三轴度在负轴方向的绝对值增大而提高。GTN损伤模型从微观孔洞形核、长大和聚合的角度解释了材料的破坏，可以很容易地应用到有限元软件材料模型中。在单调加载的条件下，一个修正好的GTN模型可以应用到很多工程应用中^[4]。苌群峰等^[5]通过建立考虑镁合金温度效应的韧性破裂准则，进行镁合金板材温热成形极限预测，且采用温热拉延试验进行了验证，预测结果与试验结果吻合较好。王万鹏等^[6]将Gurson塑性理论引入有限元计算中，通过单元的成核损伤来模拟粉末冶金材料在单向拉伸状态下裂纹萌生和扩展机制，模拟发现夹杂位置和夹杂形状对空穴体积增长分数和空穴成核率影响较大。WANG等^[7]通过将改进的GTN损伤模型带入ABAQUS子程序中，对不同温度下镁合金冲压成形做了研究，展开成形试验，并用电子显微镜观察了材料损伤演化过程。

镁合金结构材料具有低密度、高比强度和无污染等优点，在汽车和航空航天等领域有着广泛的应用。但因其结构特点，室温下镁合金的极限拉深比很低^[8]。国内外许多学者通过改变温度条件或成形工艺，来提高镁合金板料的成形性能^[9]。张士宏等^[10]通过电子背散射衍射(Electron back scatter diffraction, EBSD)原位跟踪观测方法对100~230℃时轧制镁合金板材在不同条件下的力学性能和织构转变特点等规律进行分析，揭示了不同变形条件下镁合金板材塑性变形机理。LIU等^[11]通过液压成形工艺对镁合金复杂截面零件进行成形，利用液压成形工艺的优势成功制得了合格零件，并且壁厚分布均匀。LEE等^[12]首次对镁合金板材高温气压成形进行研究，发现温度是对工件成形影响最重要的因素。

板材固体颗粒介质成形工艺是一种新型的软模成形工艺，通过固体颗粒介质代替刚性凸模(或凹模)的作用，对金属板材进行成形^[13]。因为采用的固体颗粒具有流动性、易密封和耐高温等优点，使得该工艺在成形复杂截面形状和高温下金属板材成形方面具有独特的优势。目前，应用固体颗粒成形工艺已经成功制得筒形件和抛物线形等典型零件^[14-15]。但是应用固体颗粒成形复杂截面零件的研究还比较少。

结合固体颗粒成形工艺的优点，本文先通过热态单向拉伸试验和有限元逆向法确定镁合金GTN损伤模型参数。将确定的损伤参数代入镁合金材料模型中，进行镁合金板材异形件固体颗粒成形模拟。研究不同工艺参数对工件质量的影响，结合GTN模型分析预测破裂趋势，分析了不同成形阶段的损伤演化规律，确定最佳成形工艺参数，并且通过试验验证了最佳工艺参数和预测结果的准确性。

1  GTN损伤模型及损伤参数的确定

1.1  GTN损伤模型

与传统塑性理论不同，Gurson损伤模型考虑了宏观静水应力对材料屈服的影响，且屈服面随着材料损伤(孔洞体积分数)的增大而减小。基于Gurson模型，TVERGAARD^[16]引入拟合参数q₁、q₂ 和q₃来描述孔洞间的相互作用。为了描述材料破裂时的孔洞聚合效应，TVERGAARD等^[17]引入损伤函数f ^*，得到GTN模型：

  (1)

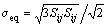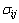式中：为宏观von Mises 等效应力；表示宏观应力的偏应力分量；其中，为流动应力分量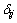；表示克罗内克记号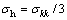；为宏观静水应力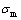；为基体材料的等效应力；q₁、q₂和q₃是表示孔洞群间相互作用的修正参数；f ^*是孔洞体积分数f的函数，表示等效孔洞体积分数。等效孔洞体积分数f ^*定义为

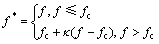                   (2)

                              (3)

式中：f_c为孔洞开始发生聚合时的临界孔洞体积分数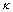；为孔洞长大加速因子；f_F为材料破裂时孔洞体积分数。

多孔材料的塑性流动与孔洞体积分数f和基体材料的累积塑性应变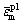都相关。由等效功原理可得基体等效塑性应变的演化方程：

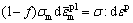                       (4)

式中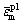：为基体材料的累积等效塑性应变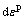；为宏观塑性应变增量。

材料的损伤演化可以分为两部分：原有孔洞的长大df_g和新孔洞形核引起的损伤变化df_n，即

                               (5)

假设基体材料不可以压缩，由质量守恒定律可知，原有孔洞的长大df_g只与宏观塑性应变的静水分量相关：

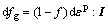                           (6)

式中：I是二阶单位张量。

df_n采用塑性应变控制形核准表示为

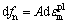                                 (7)

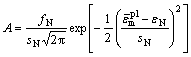              (8)

式中：A为应变控制的孔洞形核系数；f_N 形核粒子的孔洞体积分数；ε_N为形核时的平均等效塑性应变；s_N为孔洞形核应变的标准差。

1.2  损伤参数的确定

根据本构模型可以看出，GTN损伤模型包含了9个损伤参数：q₁、q₂、q₃、f₀、f_c、f_F、f_N、s_N和ε_N。只有准确地确定这些损伤参数，才能准确地预测材料的损伤断裂行为。目前，确定这些参数的方法主要有三类：代表性体积单元法，金相学分析法和有限元逆向法。有限元逆向法通过大量的模拟与试验对比，不仅节省费用，而且确定结果较为准确，故本文采用有限元逆向法。调整有限元单向拉伸模拟中的GTN参数，使得模拟真实应力应变曲线与实际单向拉伸实验结果相一致^[18]，最终确定GTN模型损伤参数。

1.2.1  单向拉伸试验

选取厚度1mm的AZ31B镁合金板为单向拉伸实验材料，其成分见表1。根据《GB/T 4338—1995 金属材料高温拉伸实验标准》设计拉伸试样尺寸，并用电火花线切割方法制取拉伸试样，见图1。在应变速率为0.01 s^-1、温度为250 ℃时进行镁合金单向伸试验。

表1  AZ31B镁合金板材成分

Table 1  Composition of AZ31B magnesium alloy sheet (mass fraction, %)

图1  单轴拉伸试样及尺寸

Fig. 1  Uniaxial tension specimen (a) and its geometric dimensions (b) (Unit: mm)

1.2.2  单向拉伸有限元模拟

采用ABAQUS软件Explicit动态显示模块模拟镁合金单向拉伸实验。模拟试样几何模型尺寸与试验实际尺寸一致，采用缩减积分实体单元C3D8R网格单元类型，厚度方向划分为2层单元。按照拉伸试验获得的力学性能参数输入材料属性。模拟边界条件的设置与实际拉伸试验相同，即拉伸试样的一端完全固定，另一端采用位移加载。在GTN损伤模型的9个损伤参数中，根据Tvergaard建议，采用对大多数金属都适用的修正参数，分别为q₁=1.5、q₂=1和q₃=2.25。将模拟后输出的真实应力应变曲线与试验真实应力应变曲线对比，取最吻合的一组参数。最终确定的GTN损伤参数见表2，其真实应力-应变曲线对比见图2。

表2  镁合金GTN模型损伤参数

Table 2  Damage parameters of magnesium alloy GTN model

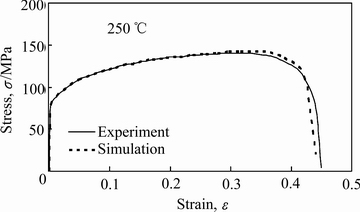
图2  模拟与真实应力-应变曲线对比

Fig. 2  Comparison of stress-strain curves between experiment and simulation

2  AZ31B镁合金异形件固体颗粒拉深成形数值模拟

2.1  零件特征分析及有限元模型的建立

零件三维模型及截面基本尺寸见图3。该零件的宽度为20mm，开口底部长宽比为3:2，零件底部形状复杂，其中心处有一个阶梯凸筋，左侧主要由两个拔模面组成，右侧是一个中心回转曲面。为节省计算时间，采用ABAQUS建立1/2对称有限元模型，如图4所示。除颗粒为三维变形实体外，其余都是壳体类型。将前述确定的GTN参数代入ABAQUS镁合金材料属性中，板材厚度t为0.8mm。颗粒的材料属性采用拓展的Drucker-Prager线性模型^[15]，由试验测试获得相关参数取值，颗粒材料的内摩擦角β为31.4°，三轴拉伸屈服应力与三轴压缩屈服应力之比K为0.83，颗粒剪胀角ψ为15.7°；D-P硬化模型结果为p=770.44ε_V，其中p为颗粒介质承受压力，ε_V为颗粒体积压缩率。颗粒与板材的摩擦因数为0.2。边界条件为凹模和料筒固定，冲头匀速向下运动，采用位移控制。以不同板坯形状，不同压边间隙和不同板材与模具摩擦因数对成形工艺参数进行研究。

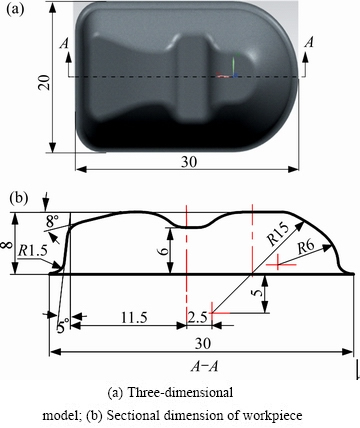
图3  零件特征分析

Fig. 3  Part feature analysis (Unit: mm)

图4  颗粒介质成形有限元模型

Fig. 4  Finite element model of SGMF

2.2  有限元模拟结果分析

2.2.1  板坯形状的选择

坯料的形状是零件成形首要考虑的因素，合理的坯料形状不仅能节约材料，而且对于其他成形参数的确定至关重要。在其他参数一样的情况下(压边间隙1.04t，板材与模具摩擦因数0.15)，根据工艺特征和变形前后体积不变条件，本文采用直径36.5 mm圆形坯料(见图5(a))以及与工件法兰形状近似的异形坯料(见图5(b)，坯料总长36.5 mm，头部半圆半径14 mm)分别进行拉深成形模拟，得到工件成形高度为7.5 mm左右时，沿高度方向(Z向)的位移云图见图5。相比于异形坯料，圆形坯料的工件在法兰圆角处极易发生破裂，且其法兰收料不均匀。因此，本工艺最终采用异形坯料。

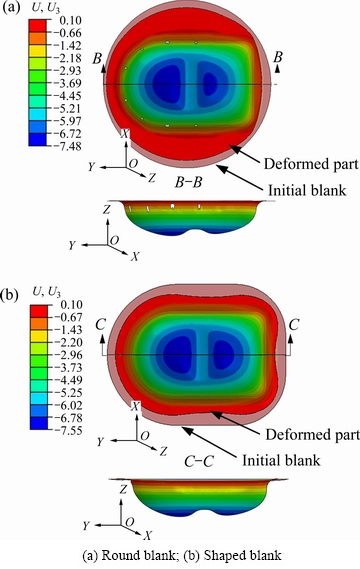
图5  两种形状原始板坯拉深成形Z向位移云图

Fig. 5  Displacement nephograms in Z direction of two initial blanks forming

2.2.2  拉深成形过程分析

根据该异形工件在颗粒介质拉深成形过程中的变形特点，可将其成形分为3个阶段: 第一阶段如图6(a)所示的自由变形阶段，此时工件成形高度H＜6 mm，该阶段主要以法兰区板材收料产生拉深成形；第二阶段如图6(b)所示的底部阶梯贴模阶段，此时成形高度6 mm≤H＜8 mm，此阶段工件底部与凹模中间的阶梯相接触，并逐渐向阶梯两侧贴模成形；第三阶段如图6(c)所示的底部和侧壁贴模阶段，此阶段成形高度H=8 mm，主要完成侧壁及底部局部特征充填成形。

为此，根据工件形状特点可将工件分为如图6(d)所示的4个主要变形区：A(A₁、A₂)凹模圆角区、B侧壁凹模圆角区、C底部阶梯圆角区和D(D₁、D₂)底部侧壁贴模区。

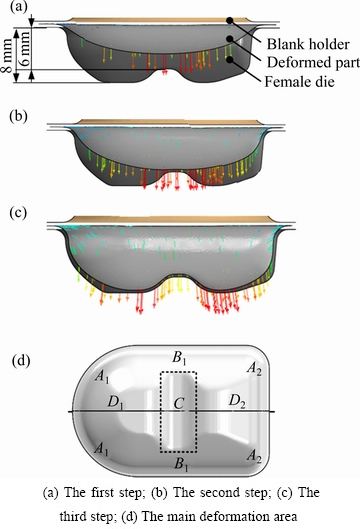
图6  工件变形3个阶段及变形区

Fig. 6  Three deformation steps and deformation regions of the workpiece

2.2.3  摩擦因数对孔洞体积分数和等效应变的影响

本研究中采用间隙控制进行异形工件的拉深成形，在压边间隙为1.12t的条件下，分别将板材和模具摩擦因数μ设定为0.05、0.15和0.25，研究其对成形的影响，图7所示为3种条件下最终成形工件孔洞体积分数(VVF)云图。孔洞体积分数f表示工件的损伤程度，其数值越大表示材料损伤越严重。由前述研究确定本研究中的镁合金板材发生材料破裂时孔洞体积分数f_F=0.0657，达到此条件下的材料单元会消失。

图7  不同摩擦因数下孔洞体积分数云图

Fig. 7  Void volume fraction nephograms at different friction coefficients

由图7可知，工件成形中的侧壁圆角处(B区)和底部阶梯圆角处(C区)是容易产生破裂的危险区域。当板材与模具的摩擦因数μ=0.25时，板材B区侧壁圆角和C区底部阶梯圆角都已经发生了断裂。随着摩擦因数的减小，B区侧壁和C区底部阶梯圆角的孔洞体积分数都逐渐减小，即破裂趋势下降。这是因为摩擦因数越小，板材在法兰和凹模侧壁处收料越容易。当μ=0.05时，B区侧壁法兰的孔洞体积分数已经很小，虽然C区圆角处孔洞体积分数还是最大值，但并没有发生破裂。

为研究C区材料断裂损伤的演化过程，分析了μ=0.15时板材底部阶梯圆角处的5个单元(见图8)的孔洞体积分数和等效应变演化过程，其结果如图9所示。

图8  断裂危险区的5个单元

Fig. 8  Five elements at fracture risk regions

图9  孔洞体积分数和等效应变演化过程

Fig. 9  Evolutionary process of void volume fraction (a) and equivalent strain (b)

从图9(a)中不同单元的孔洞体积分数演化过程可以看出，在压头行程至4.2 mm前，此时工件处于成形的第一变形阶段，板材发生了较小的塑性变形。不同单元的孔洞体积分数基本相同，说明各单元塑性变形均匀；材料内部主要处于原始孔洞长大阶段，各单元孔洞体积分数较小且增长缓慢；当压头行程在4.2~5.3 mm时，各单元孔洞分数基本一致，但是由于发生了较大塑性变形，各单元孔洞体积分数增长速度加快，此阶段在原有孔洞长大的同时也有新的孔洞形核；在压头行程为5.3 mm至最后的贴模阶段，各单元孔洞体积分数增长速率开始出现差异，板材开始发生局部集中变形，孔洞体积分数迅速增大。1号单元和2号单元增长速率较快，孔洞体积分数都达到了临界孔洞体积分数f_c=0.0318，材料内部孔洞之间开始发生聚合，而1号单元孔洞体积分数最后达到断裂孔洞体积分数0.0657，材料发生断裂。3号单元、4号单元和5号单元孔洞体积分数增长缓慢，孔洞体积分数最终并未达到临界值。

材料等效应变的变化规律与孔洞体积分数的演化过程相似(见图9(b))。当压头行程为5.3 mm前，各单元等效应变数值和增长趋势基本相同，表明板材变形均匀。当压头行程为5.3 mm至最后的贴模阶段，各单元等效应变开始分离并迅速增大，材料发生局部集中变形。

为探讨摩擦条件对板材成形的影响，通过改变板材与模具间摩擦因数并调整其分布状态，进行了拉深过程仿真模拟分析。研究发现，板材的B区侧壁破裂危险区可以通过适当减小摩擦因数(整体摩擦板材与模具间摩擦因数均为0.05)，避免侧壁破裂。这是因为摩擦因数降低，法兰和凹模圆角处板材更容易向凹模内流动，但要在实际生产中保证板料与模具间0.05的摩擦因数，将对模具制造及润滑提出较高要求。C区底部圆角区破裂趋势虽然减小，但仍是最危险区域，原因在于板材在C区贴膜后，继续依靠胀形减薄向两侧(D₁区和D₂区)实现成形。为抑制板材C区贴模后向两边胀形减薄，促使法兰区板材继续补料实现D区贴模成形，可以通过加大C区摩擦因数，因此提出一种新的摩擦方案：将C区模具与板材摩擦因数设置为0.25，其余部分为0.15(简写为μ=0.25 & 0.15)。图10所示为不同摩擦因数下成形过程中断裂危险区1号单元的孔洞体积分数演化规律。

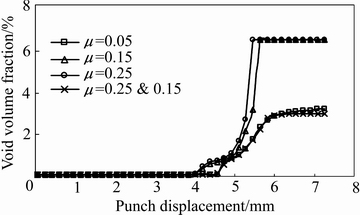
图10  不同摩擦条件下1号单元的孔洞体积分数的演化过程

Fig. 10  Evolution process of void volume fraction of element 1 at different friction coefficients

由图10可以看出，在压头行程的前4.2 mm内，板材内部孔洞体积分数很小且基本相同；在后面的成形过程中，当板材和模具的整体摩擦因数分别为μ=0.15和μ=0.25两种条件下，孔洞长大、聚合速度较大，孔洞体积分数最终达到断裂孔洞体积分数0.0657，材料发生破裂。相比之下，在摩擦条件为μ=0.05和μ=0.25 & 0.15两种条件下，最终孔洞体积分数增长缓慢，工件最终没有发生断裂。但μ=0.05对于试验条件要求更为严格，而采用μ=0.25 & 0.15的条件更具有实际意义。

3  试验模拟对比分析

3.1  镁合金异形件固体颗粒成形试验装置及过程

固体颗粒成形作为一种新的软模成形技术，因颗粒介质具有流动性、易密封和耐高温等优点，使其在复杂截面零件高温成形中占有独特的优势。镁合金异形件固体颗粒成形实验原理和设备如图11所示，采用Linkreal WDD-LCJ-150电子多功能扭转试验机提供成形力，料筒上均匀分布的八个加热棒对模具进行加热，利用电偶式温控箱控制成形温度为250 ℃。压边间隙采用在板材附近添加不同厚度的垫板的方法控制，润滑剂为水基二硫化钼。先将SiO₂颗粒介质放入料筒内，将模具加热达到250 ℃后，放入板材保温2 min。冲头在料筒里固定，凹模在试验机的作用下以匀速v向下移动，采用位移控制。成形完成后，料筒底部四根均匀分布的弹簧将料筒退回原位置。

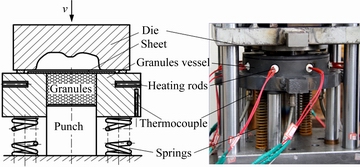
图11  试验原理及装置图

Fig. 11  Experiment schematic diagram and experiment setup

3.2  结果与分析

为了验证耦合GTN损伤断裂准则的异形件固体颗粒有限元模型的准确性，选取异形坯料，在压边间隙为1.12t和无润滑条件下进行成形，最终的试验工件沿中间对称截面切开量取厚度。并将试验厚度结果与在相同路径下压边间隙为1.12t、板材与模具摩擦因数为0.25时模拟得到的厚度进行对比，其结果如图12所示。试验与模拟壁厚变化总趋势相同，即法兰处增厚，凹模内减薄，且其底部凸筋处为减薄最严重区域。试验和模拟工件都在C区阶梯圆角处发生减薄和破裂，在其余地方减薄均匀。试验工件沿对称轴总长度为34.7 mm大于其模拟值30.7 mm，说明试验时收料比模拟相对较少。试验和模拟工件壁厚相对误差在18%以内。分析产生误差的原因在于试验采用无粘聚力的散体颗粒介质，而模拟时采用的Drucker-Prager 线性本构模型是基于连续介质模型而建立的，该模型并不能准确反映出试验中散体颗粒间力的传递方式及规律，因此会造成颗粒底部压力值与实际试验值有所差距即拉深异形坯料的成形力也会与试验值有所差异。

图12  试验与模拟的壁厚曲线对比

Fig. 12  Wall thickness comparison between experiment and simulation

图13  模拟与试验成形工件中孔洞体积分数云图

Fig. 13  Comparison of void volume fraction nephograms of workpieces between experiment and simulation

在压边间隙为1.04t且板坯整体采用水基石墨润滑的条件下，对异形坯料进行拉深模拟分析，其孔洞体积分数(VVF)云图如图13(a)所示，在工件侧壁沿法兰圆角和底部阶梯圆角部位出现破裂，与试验成形结果基本吻合。当压边间隙为1.12 t、仅板坯法兰处进行水基石墨润滑时，成功制备出合格的零件(见图13(b))，相同条件下的模拟分析结果和试验保持了一致，证明基于GTN模对镁合金异形件颗粒介质成形进行分析的有效性。

4  结论

1) 通过热态下镁合金单向拉伸试验和有限元逆向法，确定了镁合金GTN模型的损伤参数。基于镁合金GTN损伤模型，采用ABAQUS有限元软件，对圆形和近似工件法兰外沿形状两种不同形状坯料、不同摩擦因数的工艺参数进行镁合金板材固体颗粒成形模拟。分析表明，近似工件法兰外沿形状坯料更有利于工件拉深成形。通过拉深成形中异形件孔洞体积分数云图，预测了其破裂危险区域为长边法兰处和零件底部圆角处。采用局部摩擦控制的方法，中间凸筋位置设置μ=0.25、其余部位μ=0.15的条件可以顺利拉深成形，其成形结果与整体摩擦因数μ=0.05时的相当，因此，在操作中更具有实际意义。

2) 在250 ℃时，针对不同工艺参数展开了镁合金异形件固体颗粒介质成形试验。结果表明，该损伤模型能够较好地描述板材在固体颗粒成形过程中的损伤断裂演化过程。试验与模拟工件的壁厚变化总体趋势相同，最大壁厚相对误差为18%，且该镁合金GTN模型成功预测了镁合金板材在成形中的破裂位置。验证了GTN损伤参数和模拟确定的最佳成形工艺参数的正确性。为使用GTN模型研究镁合金固体颗粒成形其他复杂截面形状零件奠定了基础。

REFERENCES

[1] 余海燕, 王 友. 5052铝合金冲压成形过程中韧性断裂的仿真研究[J]. 中国有色金属学报, 2015, 25(11): 2975-2981.

YU Hai-yan, WANG You. Bulging simulation of ductile fracture of 5052 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2015, 25(11): 2975-2981.

[2] 黄建科. 金属成形过程的细观损伤力学模型及韧性断裂准则研究[D]. 上海: 上海交通大学, 2009: 2-5.

HUANG Jian-ke. Study on meso-damage model and ductile fracture criterion in metal forming processes[D]. Shanghai: Shanghai Jiao Tong University, 2009: 2-5.

[3] TENG Bu-gang, YUAN Shi-jian, CHEN Zeng-tao, JIN Xue-run. Plastic damage of T-shape hydroforming[J]. Transactions of Nonferrous Metals Society of China, 2012, 22(S1): s294-s301.

[4] KIRAN R, KHANDELWAL K. Computational models for ductile fracture prediction in structural engineering applications[J]. Procedia Materials Science, 2014, 3: 1947-1955.

[5] 苌群峰, 彭颖红, 杜朝辉. 镁合金板材温热成形韧性破裂准则[J]. 机械工程学报, 2009, 45(10): 294-299.

CHANG Qun-feng, PENG Ying-hong, DU Zhao-hui. Ductile fracture criterion for warm deep drawing of magnesium alloy sheet[J]. Journal of Mechanical Engineering, 2009, 45(10): 294-299.

[6] 王万鹏, 岳珠峰, 杨治国. 含夹杂粉末冶金材料拉伸试件的损伤分析[J]. 中国有色金属学报, 2004, 14(6): 949-955.

WANG Wan-peng, YUE Zhu-feng, YANG Zhi-guo. Damage analysis of tensile specimens of powder metallurgy material including voids[J]. The Chinese Journal of Nonferrous Metals, 2004, 14(6): 949-955.

[7] WANG Rui-ze, CHEN Zhang-hua, LI Yu-jie, DONG Chao-fang. Failure analysis of AZ31 magnesium alloy sheets based on the extended GTN damage model[J]. International Journal of Minerals Metallurgy & Materials, 2013, 20(12): 1198-1207.

[8] 于彦东, 李彩霞. 镁合金AZ31B板材热拉深成形工艺参数优化[J]. 中国有色金属学报, 2006, 16(5): 786-792.

YU Yan-dong, LI Cai-xia. Optimization of processing parameters for magnesium alloy AZ31B sheets in thermal deep drawing process[J]. The Chinese Journal of Nonferrous Metals, 2006, 16(5): 786-792.

[9] 郜 瑞, 温 彤, 季筱玮, 张文城. 镁合金板材拉深工艺的研究与进展[J]. 热加工工艺, 2012, 41(5): 30-32.

GAO Rui, WEN Tong, JI Xiao-wei, ZHANG Wen-cheng. Research and Development of drawing technology for magnesium alloy[J]. Hot Working Technology, 2012, 41(5): 30-32.

[10] 张士宏, 宋广胜, 宋鸿武, 程 明. 镁合金板材温热变形机理及温热成形技术[J]. 机械工程学报, 2012, 48(18): 28-34.

ZHANG Shi-hong, SONG Guang-sheng, SONG Hong-wu, CHENG Ming. Deformation mechanism and warm forming technology for magnesium alloys sheets[J]. Journal of Mechanical Engineering, 2012, 48(18): 28-34.

[11] VIEHWEGER B, RICHTER G, DüRING M, KARABET A, LIUXin,XU Yong-chao, YUAN Shi-jian. Hydro-forming of aluminum alloy complex-shaped components[J]. Transactions of Nonferrous MetalsSocietyofChina,2011,21(S2): s417-s422.

[12] LEE S, CHEN Y H, WANG J Y. Isothermal sheet formability of magnesium alloy AZ31 and AZ61[J]. Journal of Materials Processing Technology, 2002, 124: 19-24.

[13] 赵长财, 李晓丹, 董国疆, 王银思. 板料固体颗粒介质成形新工艺及其数值模拟[J]. 机械工程学报, 2009, 45(6): 211-215.

ZHAO Chang-cai, LI Xiao-dan, DONG Guo-jiang, WANG Yin-si. Solid granules medium forming technology and its numerical simulation[J]. Journal of Mechanical Engineering, 2009, 45(6): 211-215.

[14] 曹秒艳, 赵长财, 董国疆. 镁合金板材颗粒介质拉深工艺参数数值模拟[J]. 中国有色金属学报, 2012, 22(11): 2992-2999.

CAO Miao-yan, ZHAO Chang-cai, DONG Guo-jiang. Numerical simulation on granules medium drawing process parameters of magnesium alloy sheet[J]. The Chinese Journal of Nonferrous Metals, 2012, 22(11): 2992-2999.

[15] DONG Guo-jiang, ZHAO Chang-cai, CAO Miao-yan. Flexible-die forming process with solid granule medium on sheet metal[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(9): 2666-2677.

[16] TVERGAARD V. Influence of voids on shear band instabilities under plane strain conditions[J]. International Journal of Fracture, 1981, 17(4): 389-407.

[17] TVERGAARD V, NEEDLEMAN A. Analysis of the cup-cone fracture in a round tensile bar[J]. Acta Metallurgica, 1984, 32(1): 157-169.

[18] 盈 亮, 刘文权, 王丹彤, 胡 平, 王 琪. 7075-T6铝合金温成形损伤演化试验与仿真[J]. 中国有色金属学报, 2016, 26(7): 1383-1390.

YING Liang, LIU Wen-quan, WANG Dan-tong, HU Ping, WANG Qi. Experimental and simulation of damage evolution behavior for 7075-T6 aluminum alloy in warm forming[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(7): 1383-1390.

Solid granules medium forming of magnesium alloy special shaped part based on GTN model

CAO Miao-yan¹, ZUO Miao-miao¹, WANG Peng¹, HAO Hai-bin², ZHAO Chang-cai², LI Jian-chao²

(1. National Engineering Research Center for Equipment and Technology of Cold Strip Rolling, Yanshan University, Qinhuangdao 066004, China;

2. Key Laboratory of Advanced Forging and Stamping Technology and Science, Ministry of Education, Yanshan University, Qinhuangdao 066004, China)

Abstract: The magnesium alloy part with complex section was researched based on solid granule medium forming (SGMF). Combined with magnesium alloy tensile test at high temperature and inverse finite element method, Gurson-Tvergaard-Needleman(GTN) parameters of magnesium alloy were obtained which can predict magnesium alloy forming limit. Based on magnesium alloy GTN model, magnesium alloy special shaped part forming process was simulated by ABAQUS. Wall thickness and void volume fraction of workpiece were analyzed with different technological parameters, and the optimum technological parameter was identified. Experimental dies of special shaped part were designed, and corresponding forming experiments were carried out. The experiment results are in good agreement with that of magnesium alloy by predicted GTN model, and qualified part is obtained with optimum technological parameter.

Key words: magnesium alloy; special shaped part; GTN model; granule medium

Foundation item: Projects(51775480, 51305385) supported by the National Natural Science Foundation of China; Project(E2018203143) supported by the Natural Science Foundation of Hebei Province, China; Project (15LGA018) supported by Young Teachers’ Independent Research of Yanshan University, China

Received date: 2018-01-10; Accepted date: 2018-09-10

Corresponding author: ZHAO Chang-cai; Tel: +86-18533511399; E-mail: zhao1964@ysu.edu.cn

(编辑  龙怀中)

基金项目：国家自然科学基金资助项目(51775480，51305385)；河北省自然科学基金资助项目(E2018203143)；燕山大学青年教师自主研究计划课题(15LGA018)

收稿日期：2018-01-10；修订日期：2018-09-10

通信作者：赵长财，教授，博士；电话：18533511399；E-mail：zhao1964@ysu.edu.cn