文章编号:1004-0609(2011)04-0727-06
基于非线性超声调制频谱识别铝合金板材的疲劳裂纹
高桂丽1,李大勇1, 2,石德全1,董静薇2
(1. 哈尔滨理工大学 材料科学与工程学院,哈尔滨 150040;
2. 哈尔滨理工大学 测控技术与通信学院,哈尔滨 150040)
摘 要:基于非线性超声调制频谱法,对航空铝合金板材中的疲劳裂纹识别进行研究;以两个不同频率的超声兰姆波为激励信号,依靠超声换能器、波形发生器和激光测振仪等,对含有疲劳裂纹和无损伤的2024-T351铝合金薄板试样进行对比实验;分别采用时域、频域和时频域联合法分析非线性超声波在铝合金薄板试样中传播的响应信号。结果表明:非线性声学特征即调制频谱及三阶谐波可作为识别2024-T351铝合金板材介质中疲劳裂纹的判据,通过对试样表面进行扫描,建立调制频谱的峰值幅度与位移的关系,据此可确定样板中疲劳裂纹的位置和轮廓,这为航空铝合金板材疲劳裂纹的识别提供更多技术支撑。
关键词:2024铝合金;薄板;非线性声学特征;调制频谱;疲劳裂纹
中图分类号:TB31;TB52 文献标志码:A
Identification of fatigue cracks in aluminum alloy plates based on nonlinear ultrasonic modulation spectrum
GAO Gui-li1, LI Da-yong1, 2, SHI De-quan1, DONG Jing-wei2
(1. School of Material Science and Engineering, Harbin University of Science and Technology, Harbin 150040, China;
2. School of Measurement-Control Technology and Communications Engineering,
Harbin University of Science and Technology, Harbin 150040, China)
Abstract: The identification of fatigue cracks in the aviation aluminum alloy plates based on nonlinear ultrasonic modulation spectrum method was studied. Taking two different frequencies nonlinear Lamb wave as actuators, comparative experiments on two types of 2024-T351 aluminum alloy plate samples, with and without fatigue crack, were performed by using ultrasonic transducer, waveform generator and non-contact laser vibration meter and so on. The ultrasonic response signals during propagation were analyzed by the time domain, frequency domain and time-frequency domain methods, respectively. The results show that the acoustic characteristic of the modulation frequency components and the third harmonics can be used to indicate the presence of fatigue cracks in 2024-T351 aluminum alloy plates. By scanning the cracked plate, a relationship between the modulation frequency peak magnitude and scanning displacement was established, and according to this relationship the fatigue cracks can be located approximately, the crack contour can be obtained, which will provide more technical support for identification fatigue cracks in aviation aluminum alloy plate.
Key words: 2024 aluminum alloy; plates; nonlinear acoustic characteristic; modulation spectrum; fatigue cracks
2024铝合金属于Al-Cu-Mg系列热强化铝合金,2024铝合金板材在航空航航天等领域有着广泛应用,如作为飞机蒙皮、宇宙飞船壁板、机身框架等重要承力构件和结构件[1-2]。然而,2024铝合金具有质软、易出现沿晶型局部腐蚀等弱点,且航空铝合金工作环境条件复杂,通常要承受较高的循环载荷,这使得在铆钉或螺栓连接处极易产生应力集中并萌发疲劳裂纹。为避免由于疲劳裂纹而引发的事故,研究2024铝合金板材微疲劳裂纹监测技术十分必要[3-4]。
超声兰姆波具有快速高效的特点,特别适合板型结构的大面积无损检测。兰姆波在板中传播时,结构内部的各种损伤所引起的应力集中、裂纹扩展都会引起结构中传播的兰姆波信号的散射和能量吸收[5-7]。但是,由于兰姆波的频散和多模式特性,使得检测变得非常复杂。兰姆波检测的重点在于缺陷信号的提取和精确信号的解释[8-9]。利用非线性超声兰姆波调制频谱可在很大程度上简化信号处理和分析过程,并且对铝合金板中的缺陷尤其是疲劳裂纹具有很高的识别能力。
本文作者利用差频超声波非线性调制声学,以含有疲劳裂纹和无缺陷2024-T351铝合金薄板为研究对象,采用时域、频域和时频联合分析方法分析介质中的响应信号,以期获得航空铝合金疲劳裂纹识别的参考依据。
1 板材介质非线性声学调制的基本原理
声波在非线性介质中传播时,会产生不同程度的波形畸变。典型的现象就是当单一频率的声波在介质中传播时,会产生高阶谐波现象。然而,对于铝合金板材来说,在有限幅度条件下,产生二次谐波并不容易,然而,当介质中存在多个波动形成的位移场时,就会产生不同频率波之间的调制现象。这与非线性超声高阶谐波现象相似,非线性调制现象是材料非线性声学的另一种表现形式。
在非线性声学中,一维情况下的应力与应变的关系可由广义胡克定律描述[10]。当介质为板材时,一维非线性弹性波动方程可表示为[11]
 (1)
(1)
式中:c为声波在介质中传播速度;x为声波传播的距离; 为非线性声学特征系数;u为质点振动位移,它与应变
为非线性声学特征系数;u为质点振动位移,它与应变 之间的关系为
之间的关系为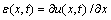 。
。
根据波扰动理论,并利用逐步近似求解法求解时,可设式(1)的解为
 (2)
(2)
式中:u(1)表示由于非线性引起的位移。若假定u(1)与波传播的方向成正比,则:
 (3)
(3)
式中: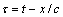 ;而
;而 为待定的未知函数。
为待定的未知函数。
现假设输入两个频率的超声信号,即
 (4)
(4)
式中:A1、A2为谐波幅值;f1、f2分别为两谐波的中心频率,与波速c、波数ki的关系为 。
。
将式(4)和(3)代入式(2),进一步代入式(1)可得到:

 (5)
(5)
故可求得质点振动位移u(x, t)为

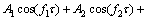
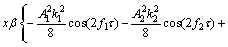
 (6)
(6)
从式(6)可以看出,除了信号频率f1和f2以外,还产生了高频谐波2f1和2f2以及调制信号频率成分,即 和
和 。因此,调幅现象可以理解为在两个以上位移场的叠加情况下出现的材料非线性超声现象。
。因此,调幅现象可以理解为在两个以上位移场的叠加情况下出现的材料非线性超声现象。
2 实验
2.1 试样制备
实验样板选用两块2024-T351铝合金薄板,它们具有相同的尺寸(140 mm×120 mm×1.5 mm)。其主要化学成分如下:Al 93.63%,Si 0.09%,Fe 0.21%,Cu 4.06%,Mn 0.47%,Mg 1.37%,Cr 0.01%,Zn 0.14%。首先用线切割机沿试样宽度方向切出长0.5 mm的切口,然后在疲劳试验机上预制疲劳裂纹,由CCD同步监测裂纹扩展情况,并将图像传至计算机,当裂纹长度扩展至约5 mm时,即制得所要求的裂纹,裂纹的部分形貌如图1所示。
2.2 实验系统构成
实验系统装置示意图如图2所示。该装置主要由压电传感器、激光测振仪、任意波形发生器、数字示波器和计算机等构成。实验中,采用两个压电传感器

图1 试样中预制的疲劳裂纹形貌
Fig.1 Morphology of prefabricated fatigue crack in sample

图2 实验系统装置示意图
Fig.2 Sketch map of experimental system: 1—Computer; 2—Power amplifier; 3—Waveform generator; 4—Laser vibrometer; 5—Digital oscilloscope; 6—Sample
作为发射换能器,其直径为8 mm,采用专用粘结剂粘在被测试样的一端。可编程任意波形发生器同时发出两个单频猝发兰姆波信号,其中一个为高频信号,中心频率为1 MHz;另一个为低频信号,中心频率为80 kHz。同时激励两个发射换能器,经功率放大器后同时加载到压电传感器上,在试样另一端,通过激光测振仪实时精确接收超声兰姆波信号,接收到的信号可同步传给可编程的数字示波器和计算机,实现对接收信号的进一步分析处理。
3 结果与讨论
3.1 时域信号分析
图3所示为接收信号的时域波形。由图3(a)可知,在时域波形中,含有疲劳裂纹样板的波形出现了较大畸变,而且波形包络(波包)之间相互叠加。而无缺陷样板的波形畸变程度较小,如图3(b)所示。对此可做如下解释。
存在疲劳裂纹的2024-T351铝合金薄板具有明显的非线性声学特征,超声兰姆波传播过程的非线性声学特征主要来自数量级更大的局部体积缺陷,且大大超过了原来体积较小的原子非线性效应,从而引发超声波波形的畸变、叠加、谐波的产生等,同时,也使得非线性声学特征更容易被测量;而在无缺陷的铝合金薄板中,内部的弹性力源于原子间的作用力,超声波在无缺陷区域传播过程中的非线性主要是原子间的非线性畸变,所以波形畸变不明显,并且产生的能量幅度较低,一般很难测量[12-13]。

图3 接收信号的时域波形
Fig.3 Time domain waveform of received signal: (a) Cracked sample; (b) Intact sample
3.2 频域信号分析
对图3中的时域信号进行频域分析,其结果如图4所示。从图4(a)可以看出,在含疲劳裂纹的样板 中,除了两激励声源的基频频率成分(f1=80 kHz,f2=1 MHz)之外,还产生新的频率成分,即调制频率成分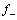 、
、 (
( =0.92 MHz,
=0.92 MHz, =1.08 MHz)以及高阶谐波
=1.08 MHz)以及高阶谐波 和
和 ,但是,二阶谐波幅度较低。而在无缺陷的样板中(见图4(b)),几乎没有新的频率成分出现,两个激励声源频率成分占主导,与图4(a)相似,二阶谐波的幅度也极低,这可能是由于
,但是,二阶谐波幅度较低。而在无缺陷的样板中(见图4(b)),几乎没有新的频率成分出现,两个激励声源频率成分占主导,与图4(a)相似,二阶谐波的幅度也极低,这可能是由于

图4 接收信号的频域图谱
Fig.4 Frequency domain spectrum of received signal: (a) Cracked sample; (b) Intact sample
测量设备所引发的非线性干扰[14]。对以上实验结果可解释如下。
超声波在介质中传播的实质是介质中的质点产生振动。存在疲劳裂纹的铝合金薄板中,将产生局部扰动,这将影响其非线性动态响应。正如1节中所分析的,当介质中存在多个波动并形成位移场时,不同频率波之间将出现调制现象。此时被测介质中同时加载两个超声波信号,使得疲劳裂纹不再保持单一的状态(张开或闭合),而是随着声源发出的激励脉冲,裂纹处于交替张开与闭合状态[15]。也就是说,可以把疲劳裂纹看作一条狭长的“微裂缝”,当加载低频波信号f1时,裂纹的状态将发生变化,随着低频信号振动相的变化而变化。如果低频波信号的振幅足够大,其压缩相可使裂纹完全闭合;相反,在随后而来的扩张相又将使裂纹处于张开状态。这时,若在介质中同步加载高频波信号f2,当低频波信号处于扩张相使裂纹张开时,此时高频波信号幅度将被削弱,高频波信号与低频波信号叠加相的幅度也将降低。相反地,当低频波信号处于压缩相使裂纹闭合时,高频波的幅度将不会损失,此时高频波信号与低频波信号的叠加相幅度将增加。
因此,在含有疲劳裂纹的2024-T351铝合金薄板中,由于“非线性散射体”(裂纹)的存在,使得在介质中传播的两超声兰姆波信号在幅值上产生相互调制(见图3(a)),在时域波形中,将会出现波形畸变。通过频谱分析,便会看到调制频率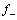 和
和 及高次谐波
及高次谐波 等,如图4(a)所示。而在无缺陷的铝合金薄板中,响应信号来自“线性散射体(样板边缘)”,将不会出现调制频率成分,如图4(b)所示。
等,如图4(a)所示。而在无缺陷的铝合金薄板中,响应信号来自“线性散射体(样板边缘)”,将不会出现调制频率成分,如图4(b)所示。
此外,从图4(a)中可看出,在含有疲劳裂纹的介质中,所有高阶谐波中三阶谐波的幅度较明显。其主要原因是由于出现损伤的铝合金板材滞回效应,在非线性声学中,当介质中没有缺陷或损伤时,声波在介质中传播可用一维情况下的应力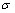 与应变
与应变 的关系来描述。
的关系来描述。
而当金属板材介质中存在疲劳裂纹时,其整体力学性能可以用损伤力学或材料的非线性本构关系来描述,但在微观上,其非线性特性由于裂隙上的接触问题而变得十分复杂。金属介质出现开裂情况时,材料内部出现交界面,外部波动的应力作用下,会改变接触面的形态,导致材料出现非线性响应,介质中将会产生滞回现象,此时弹性模量可表示为

 (9)
(9)
式中: 为二阶非线性系数;
为二阶非线性系数; 为三阶非线性系数,
为三阶非线性系数, 表示为滞回介质中应力与应变的关系,其中
表示为滞回介质中应力与应变的关系,其中 为非线性参数,反映了材料介质中的滞回效应;
为非线性参数,反映了材料介质中的滞回效应; 为应变率,
为应变率, 为平均应变幅度,如果
为平均应变幅度,如果  >0,则
>0,则 ,如果
,如果 <0,
<0,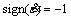 。
。
在经典非线性系统中,频率为f、应变幅度为 的超声波传播一段距离后,非线性的影响会使频率的分布发生变化,导致高阶谐波的产生,即会产生频率为2f和3f的高频成分,其对应的应变幅分别为
的超声波传播一段距离后,非线性的影响会使频率的分布发生变化,导致高阶谐波的产生,即会产生频率为2f和3f的高频成分,其对应的应变幅分别为 和
和 。而对于具有滞回效应的材料,则不会出现二阶谐波,而且三阶谐波的幅值与
。而对于具有滞回效应的材料,则不会出现二阶谐波,而且三阶谐波的幅值与 成正比。由此可见,滞回效应表现为二次效应。在调制试验中,当有激励频率为f1和f2的超声信号时,对应应变幅分别为
成正比。由此可见,滞回效应表现为二次效应。在调制试验中,当有激励频率为f1和f2的超声信号时,对应应变幅分别为 和
和 时,则会出现调制频率
时,则会出现调制频率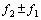 ,且将与
,且将与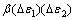 成正比,当滞回效应明显时,还会出现
成正比,当滞回效应明显时,还会出现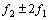 的峰值[16]。
的峰值[16]。
3.4 响应信号的时间和频率联合分析
为进一步研究响应信号的到达时间与频率成分的分布关系,对接收到的信号进行时域与频域联合分析,其结果如图5所示。这种分析方法能同时在时域和频域内分析响应信号的时频特征,是分析非平稳信号的有力工具。从如图5(a)和(b)可以看出,响应信号的频率成分与图4(a)、(b)中的频率成分相同,而且沿时间轴的方向,激励信号能量呈衰减趋势。此外,从图5(a)即含有疲劳裂纹样板中的时频图谱可看出,高次谐波和调制频率成分在同一时间出现,即时间轴为50 μs左右。在滋生频率成分中,调制频率f+=1.08 MHz的能量较高;而从无缺陷样板的时频图谱(见图5(b))中不难看出,除声源激励频率外,仅有二次谐波,但其能量极低。以上分析结果进一步验证:在含有疲劳裂纹的样板中,采用差频激励超声波,响应信号会出现明显的调制频谱和高次谐波。
因此,调制频率和高次谐波可作为判断疲劳裂纹是否存在的判据,这将为航空铝合金疲劳裂纹的有效快速识别提供重要依据。
3.5 疲劳裂纹的定位
为了实现裂纹的定位,可重复以上步骤,沿着垂

图5 接收信号的时频图谱
Fig.5 Time-frequency spectrum of received signal
直于疲劳裂纹的直线方向,用激光测振仪扫描被测铝合金薄板试样表面,并将每一接收点的信号进行窄带滤波,提取f+的时域峰值信号,并将f+峰值与扫描位移相对应,即可确定裂纹的位置,结果如图6所示。

图6 调制信号f+的峰值与裂纹位置的关系
Fig.6 Relationship between modulation signal peak and crack position
从图6中可以看出,靠近疲劳裂纹的位置,f+峰值信号幅度增加较快;在疲劳裂纹上,f+峰值信号幅度达到最大值;而远离疲劳裂纹时,f+峰值信号幅度明显降低,并且趋于相同数值。其原因是由于用差频超声波信号激励时,疲劳裂纹在薄板中处于张开与闭合的交替状态,超声波在裂纹处产生多次的反射和折射,超声波发生能量累积,使声波相互干涉叠加,调制信号峰值幅度达到最大值[17]。因此,根据激光测振仪扫描结果,便可获得疲劳裂纹的大致轮廓,结果如图7所示。从图7中可以看出,信号最高能量集中在裂纹尖部附近。这可能是裂纹扩展时裂纹尖端产生塑

图7 调制信号f+峰值能量与疲劳裂纹位置的关系
Fig.7 Relationship between modulation signal peak energy and position of fatigue crack
性区域,在此区域单元体积内所存储的应变能较 高[18],其机理还有待于进一步研究。
4 结论
1) 含有疲劳裂纹的样板中,时域波形发生较大畸变和相互叠加,其相应的时频谱中出现新的频率成分,调制频率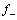 =0.92 MHz、
=0.92 MHz、 =1.08 MHz及3f2等。而无缺陷实验样板中,不出现明显的新频率成分。
=1.08 MHz及3f2等。而无缺陷实验样板中,不出现明显的新频率成分。
2) 差频超声波调制频率可作为出现疲劳裂纹的判据。利用激光测振仪对被测样板表面进行动态逐点扫描,可得出调制频率时域峰值与扫描位移的关系,依据扫描结果,可确定疲劳裂纹的位置和轮廓。
REFERENCES
[1] 张 莉, 刘文晶, 程 靳, 付德龙. 基于裂纹尖端塑性应变能对2024铝合金疲劳裂纹扩展寿命进行预测[J]. 中国机械工程, 2008, 19(4): 469-471.
ZHANG Li, LIU Wen-jing, CHENG Jin, FU De-long. Prediction of fatigue crack growth life of 2024 aluminum alloy based on the plastic energy[J]. China Mechanical Engineering, 2008, 19(4): 469-471.
[2] 刘克文, 邢 丽, 柯黎明. LY12铝合金摩擦点焊接头组织及性能[J]. 中国有色金属学报, 2008, 18(2): 288-293.
LIU Ke-wen, XING Li, KE Li-ming. Microstructures and properties of friction stir spot welding joints for LY12 aluminum alloy[J]. The Chinese Journal of Nonferrous Metals, 2008, 18(2): 288-293.
[3] BIROL Y, BIROL F. Wear properties of high-pressure die cast and thixoformed aluminium alloys for connecting rod applications in compressors[J]. Wear,2008, 265(6): 590-597.
[4] LAMAKA S V, ZHELUDKEVICH M L, YASAKAU K A, MONTEMOR M F, FERREIRA M G S. High effective organic corrosion inhibitors for 2024 aluminium alloy[J]. Electrochimica Acta, 2007, 52 (5): 7231-7247.
[5] 邓明晰. 层状固体结构表面性质的非线性兰姆波定征方法[J]. 航空学报, 2006, 27(4): 713-719.
DENG Ming-xi. Characterization of surface properties of layered structures using nonlinear lamb wave approach[J]. Acta Aeronautica Et Astronautica Sinica, 2008, 27(4): 713-719.
[6] 陈江义, 陈花玲. 弹性波在多层电磁弹性结构中的反射与透射[J]. 应用基础与工程科学, 2008, 16(4): 566-573.
CHEN Jiang-yi, CHEN Hua-ling. Reflection and transmission of elastic wave in magneto-electro-elastic multilayered structure[J]. Journal of Basic Science and Engineering, 2008, 16(4): 566-573.
[7] 唐志涛, 刘战强, 艾 兴, 万 熠. 基于裂纹柔度法的铝合金预拉伸板内部残余应力测试[J]. 中国有色金属学报, 2007, 17(9): 1404-1409.
TANG Zhi-tao, LIU Zhan-qiang, AI Xing, WAN Yi. Measuring residual stresses depth profile in pre-stretched aluminum alloy plate using crack compliance method[J]. The Chinese Journal of Nonferrous Metals, 2007, 17(9): 1404-1409.
[8] ZAITSEV V, NAZAROV V, GUSEV V B. Novel nonlinear modulation acoustic technique for crack detection[J]. NDT & E International, 2006, 39(3): 184-194.
[9] DONSKOY D, SUTIN A, EKIMOV A. Nonlinear acoustic interaction on contact interfaces and its use for nondestructive testing[J]. NDT & E International, 2001, 34(4): 231-238.
[10] KIM J Y, BALTAZAR A, HU J W, BERMES C. Hysteretic linear and nonlinear acoustic responses from pressed interfaces[J]. International Journal of Solids and Structures, 2006, 43(21): 6436-6452.
[11] BEUCLER E, STUTZMANN E, MONTAGNER J P. Surface wave higher-mode phase velocity measurements using a roller- coaster-type algorithm[J]. Geophysical Journal International, 2003,155(1): 289-307.
[12] CATTANI C, RUSHCHITSKII Y Y. Cubically nonlinear elastic waves: wave equations and methods of analysis[J]. International Applied Mechanics, 2003, 29(10): 1115-1145.
[13] NAGY P B. Fatigue damage assessment by nonlinear ultrasonic materials characterization[J]. Ultrasonics, 1998, 36(1):375-381.
[14] IBRAGIMOV NH,RUDENKO OV. Principle of an a priori use of symmetries in the theory of nonlinear waves[J]. Acoustical Physics, 2004, 50(4): 406-419.
[15] BERMES C, KIM J Y, QU J, JACOBS L J. Nonlinear Lamb waves for the detection of material nonlinearity[J]. Mechanical Systems and Signal Processing, 2008, 22(4): 638-646.
[16] MOLOTKOV I A. Hysteresis in an acoustic medium with relaxing nonlinearity and viscosity[J]. Acoustical Physics, 2008, 54(5): 626-632.
[17] ZHELDUBOVSKII AV,POGREBNIAK AD,REGUL’SKII MN. Limiting state analysis of aluminum alloys under asymmetric tension-compression cycling[J]. Strength of Materials, 2006, 38(4): 442-447.
[18] TEODOROVICH SB. Technique of measurements of elastic wave attenuation parameters[J]. Russian Journal of Nondestructive Testing, 2003, 39(6): 427-435.
(编辑 龙怀中)
基金项目:国家自然科学基金资助项目(60772104);黑龙江省留学归国人员基金资助项目(LC07C01)
收稿日期:2010-03-15;修订日期:2010-07-02
通信作者:李大勇,教授;电话:0451-86392396;E-mail: dyli@hrbust.edu.cn