J. Cent. South Univ. (2020) 27: 3013-3024

DOI: https://doi.org/10.1007/s11771-020-4525-5

Calculating changes in fractal dimension of surface cracks to quantify how the dynamic loading rate affects rock failure in deep mining

GAO Ming-zhong(高明忠)^{1, 2}, ZHANG Jian-guo(张建国)³, LI Sheng-wei(李圣伟)^{2, 4} ,WANG Man(王满)³, WANG Ying-wei(王英伟)³, CUI Peng-fei(崔鹏飞)¹

1. Guangdong Provincial Key Laboratory of Deep Earth Sciences and Geothermal Energy Exploitation and Utilization, Institute of Deep Earth Sciences and Green Energy, College of Civil and Transportation Engineering, Shenzhen University, Shenzhen 518060, China;

2. State Key Laboratory of Hydraulics and Mountain River Engineering, College of Water Resource and Hydropower, Sichuan University, Chengdu 610065, China;

3. State Key Laboratory of Coking Coal Exploitation and Comprehensive Utilization, China Pingmei Shenma Energy & Chemical Industry Group Co. Ltd., Pingdingshan 467000, China;

4. Department of Civil Engineering and Lassonde Institute, University of Toronto,Toronto, ON M5S 1A4, Canada

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: The split-Hopkinson pressure bar (SHPB) and digital image correlation (DIC) techniques are combined to analyze the dynamic compressive failure process of coal samples, and the box fractal dimension is used to quantitatively analyze the dynamic changes in the coal sample cracks under impact load conditions with different loading rates. The experimental results show that the fractal dimension can quantitatively describe the evolution process of coal fractures under dynamic load. During the dynamic compression process, the evolution of the coal sample cracks presents distinct stages. In the crack propagation stage, the fractal dimension increases rapidly with the progress of loading, and in the crack widening stage, the fractal dimension increases slowly with the progress of loading. The initiation of the crack propagation phase of the coal samples gradually occurs more quickly with increasing loading rate; the initial cracks appear earlier. At the same loading time point, when the loading rate is greater, the fractal dimension of the cracks observed in the coal sample is greater.

Key words: fractal dimension; loading rate; impact load; coal crack

Cite this article as: GAO Ming-zhong, ZHANG Jian-guo, LI Sheng-wei, WANG Man, WANG Ying-wei, CUI Peng-fei. Calculating changes in fractal dimension of surface cracks to quantify how the dynamic loading rate affects rock failure in deep mining [J]. Journal of Central South University, 2020, 27(10): 3013-3024. DOI: https://doi.org/10.1007/ s11771-020-4525-5.

1 Introduction

MANDELBROT [1] introduced the concept of fractals in the 1970s. Fractal objects can be described with a fractional dimension that indexes the complexity of patterns in the object [2]. With the maturation of fractal analysis, different measurement methods have been developed for a range of research subjects, and more than ten different specifications of fractal dimension have been developed. This branch of mathematics can be applied to the analysis of rock fractures for the sake of coal mining. Fractured rock masses are cut by joints, fissures, faults, and other structural planes due to the influence of geological tectonic stress. These properties result in the rock mass being a medium that seems to be continuous but not completely continuous, and seems to be broken but not completely broken. This complex characteristic of the fracture patterns in rock means that they are a good candidate for fractal analysis [3]. As resources in the shallow strata of the earth are depleted, resource mining activities are gradually extending to deeper deposits. Deep exploitation is becoming a common practice. The distribution of cracks in deep coal-rock masses directly affects the physical and mechanical properties of the coal-rock. JIANG et al [4] and DOU et al [5] emphasized that when the dynamic loads generated by rock fractures and collapses, fault sliding and natural earthquakes in underground coal mines propagate to the surrounding rocks of the roadway, they may induce major dynamic disasters such as rock bursts. At the same time, deep coal-seam blasting, high-energy gas fracturing [6], and instantaneous gasification and coal breaking with liquid carbon dioxide [7] have increased in popularity. These highly dynamic processes have dramatic effects on the rock body surrounding a coal deposit. A quantitative and simple tool for characterizing the dynamic response of coal-rock under impact loading could therefore be of great utility for improving the safety and efficiency of coal mining.

The dynamic response of coal-rock can be revealed in the evolution of surface cracks. Other researchers have used high-speed photography [8], real-time computed tomography scanning [9], scanning electron microscopy [10], and other technologies to observe coal under static loads. Related works have focused on the evolution of fissures. In comparison with those under static and quasistatic loading conditions, the dynamic characteristics of rock under high-strain-rate loading are more similar to those observed in real engineering projects. At the same time, the strength of the rock changes with the loading rate. Therefore, researchers have also focused on how the loading rate affects crack propagation. GONG et al [11-13] obtained energy distribution law of coal-rock combined body under high loading rate, and investigated the relationships between the dynamic triaxial compressive strength, secant modulus, peak strain, and the strain rate and confining pressure of sandstone, and developed a new empirical equation to describe the dynamic increase factor of the indirect tensile strength of the Changsha sandstone, China, under different loading rates. KLEPACZKO et al [14] tested the fracture toughness of Canadian coal subjected to different loading rates. ZIPF et al [15] studied the mixed fracture toughness of coal subjected to dynamic loading. SHAN et al [16] studied the dynamic fracture toughness of anthracite using a large-diameter split-Hopkinson pressure bar (SHPB) and formulated a constitutive model for the sample. With recent developments in image processing technology and simulating the impact destruction of coal rock under a SHPB, scholars are increasingly using high-speed cameras to record the deformation evolution of the coal-rock under an impact load. With high-speed video, image processing can be used to analyze the cracking dynamics. LUNDBERG [17] first recorded the dynamic failure of rocks under the impact of SHPBs with a high-speed camera in 1976 and found that cracks mainly propagate along the axis of the load. ZHAO et al [18, 19] used high-speed cameras and digital speckle photography to record the propagation of I-type cracks in coal with different bedding angles under impact loading. They analyzed the evolution of the fractal dimension, length, and propagation velocity of the cracks. They found that the dynamic fracture failure of a notched semicircular coal sample was mainly tensile in nature, and that the fracture toughness of the coal sample was affected by the impact velocity. As the bedding angle increased, the impact velocity tended to have less effect on the rock toughness. XIA et al [20, 21] used the Photoelastic method to study the crack propagation induced by prestressed photoelastic flat specimens such as polycarbonate and Homalite-100 under explosive load, the crack growth rate and super shear phenomenon similar to natural earthquakes are obtained. ZHANG et al [22, 23] combined the SHPB experiment with numerical simulation, and developed a predictive method based on laboratory observation to estimate glass fragments induced by debris impact. ZHAO et al [24] tested briquettes and raw coal with a customized drop-hammer test device in conjunction with ultrasonic imaging equipment and found that the fractal dimension of a raw coal fissure is larger than that of an impact-loaded briquette. They also found that as the impact load increased, the fractal dimension decreased gradually. HAN et al [25] used a SHPB for loading Brazilian discs of coal, which were recorded with high-speed photography and the digital speckle-correlation method, and investigated and analyzed the evolution characteristics of the deformation fields and displacement fields during deformation localization. LIU et al [26] analyzed high-speed photography of vertically and parallel- bedded coal rock under impact loading, and found that the coal-rock samples all cracked from the center outward and that the vertical growth of cracks was noticeably affected by the bedding angle. AI et al [27] combined image processing and deep learning methods to extract coal-rock cracks from photographs. They focused on the dynamic characteristics, evolution rules, and crack propagation characteristics of coal rock during dynamic tensile failure and found that the cracks that can be observed at the surface of a coal-rock sample during SHPB impact failure can be effectively described with fractal dimensions. They also showed that the fractal dimension of a crack pattern gradually increases over the course of impact loading.

Fractures in deep coal-rock are the main channels for gas storage, diffusion and migration. Therefore, understanding the evolution patterns of coal and rock fracture networks is the key to gas control in mining operations. However, quantitative representations of this process are lacking, especially under dynamic loading. Therefore, with a focus on the unique physical properties of coal, this paper reports the results of dynamic compression experiments conducted at different loading rates. Image processing of the samples painted with a digital speckle pattern was used to extract simple images of the surface cracks at a very fine time resolution. The fractal dimension of the crack pattern in each frame was then calculated, and we found that the fractal dimension is useful as a quantitative representation of the way in which the rock will fail under an impact load.

2 Methods

2.1 Fractal principle and definition of box dimension

Different research subjects require different specifications of the notion of fractal dimension. The common definitions of fractal dimension mainly include the Hausdorff dimension, similarity dimension, capacity dimension, information dimension, correlation dimension, and box dimension [28]. We choose the simplest of these, the box dimension, for a quantitative description of the failure state of a rock sample subjected to an impact load.

The complexity of an object is defined as follows [29]:

N=Cδ^D                                                     (1)

where δ is the magnification of the object (crack); N is the total number of boxes with side length δ required to cover the entire area; C is a constant; and D is the fractal dimension. Taking the logarithms of the two sides of the above equation results in the following expression:

lgN=lgC+Dlgδ                           (2)

The above equation indicates that lgN and lgδ have a linear relationship, and the fractal dimension D is the slope of this straight line. Therefore, the fractal dimension D can also be expressed as follows [30]:

                        (3)

When calculating the fractal dimension of crack images, the crack data are first binarized, the binary image is divided into squares with side length δ, and the number of squares containing pixels is counted as N_δ. This process is iterated for a range of values of δ to calculate the fractal dimension D from Eq. (3).

We tested cylindrical coal samples with diameters of 50 mm and heights of 25 mm. Speckle patterns were applied to the surface of the sample using an improved water transfer method [31]. To obtain high-definition images of rock samples under dynamic loading, the Photron high-speed camera system was used, as shown in Figure 1. This high-speed camera can capture photos with a resolution of 256×192 pixels at the frame rate of 80000 frames per second. High-efficiency video lights were used to illuminate the sample. For easier analysis, the camera and oscilloscope driving the pressure bar were synchronized. The incident strain signal was used to trigger the high-speed camera. The speckle pattern is no longer useful once the sample fails, so all the image analyses focus on the crack patterns extracted from the high-speed video recording of the test.

Figure 1 SHPB-digital image correlation (DIC) system

The digital speckle method mainly used the surface speckle characteristics to track and measure the movement and deformation of the object surface area. Therefore, the quality of speckle on the surface of the object directly affects the validity of the measurement results. This paper adopted the water transfer digital speckle method to create digital speckle fields due to its clear advantages in calculation accuracy and speed over those of other digital speckle field application techniques. The water transfer digital speckle field mainly includes three parts: the upper layer is a transparent protective layer; the middle layer is a printed digital speckle field; and the bottom is a layer of hydrosol stickers. The thickness of the entire water transfer paper does not exceed 0.5 mm, and the film thickness of the speckle field is only approximately 35 μm, which will not affect the deformation of the sample. To further improve the quality of speckles and obtain a clearer speckle field, considering the dark characteristic colors of coal and rock samples, in this experiment, we designed a water transfer paper with a black bottom layer and white digital speckle field. Area B in Figure 2 is the observation area of the strain field image. We also used the digital image correlation (DIC) method to analyze the strain of the coal sample during the dynamic compression process.

Figure 2 Schematic diagram of SHPB basic principle

As shown in Figure 2, A₁ and A₂ are the two sides of the sample contacting the incident bar and the transmitted bar, respectively. Strain gauges 1 and 2 are equipped on the sides with the incident bar and the transmitted bar, respectively. During the experiment, strain gauges 1 and 2 are used to measure the incident wave signal ε_i, reflected wave signal ε_r and transmitted wave signal ε_t.

The SHPB device needs to meet three basic conditions: 1) The displacement velocity of the particles must be continuous across interfaces A₁ and A₂; 2) The internal forces of the bars at interfaces A₁ and A₂ are equal; 3) The friction and axial inertia force are ignored. According to the basic assumption of the SHPB device, using the three-wave method, the dynamic stress-strain relationship of the material is obtained as follows:

                    (4)

                   (5)

                       (6)

where ε(t), σ(t) andare the strain, stress and strain rate of coal sample, respectively; c is the wave velocity of the elastic bar; A is the cross- sectional area of the elastic bar; E is the elastic modulus of the elastic bar; l_s is the length of the sample; and A_s is the cross-sectional area of the sample.

2.2 Introduction of sampling site and coal sample preparation

Our coal samples were all taken from the working face of the Ji-24130 rock protection layer of the No. 10 Mine of the Pingdingshan Coal Mine, China. The work face has an effective strike length of 709 m, an inclination width of 157-160.5 m, with an average of 158.7 m, an incision length of 156.8 m, and a coal seam inclination angle of 5.91°-23.2° with an average of 9.5°. A comprehensive description of these lithological features is shown in Figure 3. The coal seam roof of the work face includes 2.5-4.0 m of L1 limestone. Above the L1 limestone it is sandy mudstone of 3.0-4.0 m, then fine sandstone of 5.0-6.0 m, and then the Ji 17 coal seam. The thickness of the Ji 17 coal is 2.2-2.8 m. The thickness of the gangue between the Ji 16 and Ji 17 coal seams is 1.4-2.1 m. The Ji 15 and Ji 16 coal seams are 2.5-3.5 m thick, and the old roof is a layer of fine- to medium-grained sandstone thicker than 18.0 m. The base for these coal measures is a Cambrian dolomite limestone aquifer approximately 80 m thick.

Figure 3 Comprehensive description

We studied coal samples from the coal block cut by the coal cutter on the work face of the Pingmei ji-24130 rock protection layer. According to the site conditions and geological reports, the characteristics of the coal in this area are the same as those of the work face. To facilitate the drilling and preparation of coal samples for indoor study, coal blocks with dimensions of approximately 25 cm×25 cm×20 cm in dimension were selected. These blocks were wrapped with plastic film, packed in boxes, and transported to the laboratory for subsequent sample preparation.

We processed coal samples using the method recommended by the International Society of Rock Mechanics. In this method, the speed of the machine tool is reduced as much as possible, and dry drilling, dry cutting and dry grinding are used as much as possible to reduce the influence of human disturbances on the original state of the coal sample. To control the influence of the bedding angle, the drilling direction was kept parallel to the bedding direction as much as possible. The rock core was cut and polished at both ends, forming a cylinder. The two ends of these samples are parallel within 0.02 mm.

2.3 Dynamic stress balance and loading rate calculations

To ensure the effectiveness of our dynamic tests, we first verified our assumption that the samples were stressed uniformly. We analyzed the axial stress balance of the samples at the moment of impact, as shown in Figure 4. We treat the moment that the incident wave reaches the contact surface between the bar and the sample as the beginning of the test. Figure 4 shows that the sum of the incident wave and the reflected wave nearly coincides with the transmitted wave during the dynamic test. This indicates that during dynamic loading, the stresses at both ends of the sample are approximately equal, so our assumption of stress balance in the sample is appropriate.

Figure 4 Dynamic stress balance diagram

The loading rate describes the rate dependence of the compressive strength of the sample and is defined as the rate at which stress changes in the sample [32]. Compared with the strain rate, the loading rate can represent the effects of the dynamic compressive strength, so we use the loading rate as an index for describing these effects on the coal samples.

The loading rate is calculated from the change in stress in the sample over time:

                           (7)

whereis the loading rate of coal sample; t₀ is the initial time of the interval; t₁ is the end time of the interval; σ_(t0) is the stress value corresponding to time t₀; and σ_(t1) is the stress value corresponding to time t₁.

The stress changes with time are shown in Figure 5. During the period from 100 to 150 μs, the stress changes approximately linearly, and the slope of this linear segment is taken as the loading rate [33, 34]. Using this definition, the loading rate of a typical dynamic compression experiment is calculated to be 279 GPa/s.

Figure 5 Schematic diagram of loading rate calculation

3 Results

Our dynamic compression experiments on coal samples from the Pingdingshan Coal Mine, China, allow us to report the dynamic strength and fracture characteristics of coal subjected to different loading rates.

3.1 Evolution image of coal sample cracks under different loading rates

Figure 6 shows images of the cracks extracted from high-speed images with our image processing and binarization algorithms. Initially, no cracks are observed in the samples. When the loading rate is 101 GPa/s, after 340 μs of dynamic loading, cracks form and gradually lengthen along the loading direction. In the period of 440-500 μs, no new cracks appear in the sample, and the existing cracks widen. When the loading rate is 166 GPa/s, a small crack first appears along the loading axis at 320 μs. During the period of 440-500 μs, this crack widens, and no new cracks appear. At the loading rate of 279 GPa/s, all the cracks that form are aligned with the loading axis. During the period of 440-500 μs, the cracks that had fully formed by 306 μs widen considerably.

Figure 6 Evolution of cracks in samples under different loading rates

As the loading progresses, cracks evolve in the following two main stages: propagation and widening. When the loading rate is 101, 166 and 279 GPa/s, the crack propagation stage lasts for 100, 120 and 134 μs, respectively. As the loading rate increases, the crack propagation stage becomes longer because the first crack forms earlier in the loading process. During the dynamic compression test, cracks form mainly along the loading direction of the sample, and multiple cracks may appear at the same time, but the number of cracks is not obviously correlated with the crack width or the loading rate.

3.2 Fractal characteristics of coal and rock dynamic compression cracks under different loading rates

The loading rate of 279 GPa/s is taken as an example to analyze and compare the fractal dimension and crack evolution. Insets a, b, and c in Figure 7 show frames recorded by the high-speed camera at 306, 440 and 500 μs after the beginning of the test, respectively. The initial crack is observed at 306 μs, and all three cracks formed along the loading axis. As the test progressed, the cracks propagated until 440 μs. In this stage, the fractal dimension increased from 1.04 to 1.32 within 134 μs, showing an increase by 0.28 at a rate of 0.0021; Then, the cracks widened between 440 and 500 μs. At this stage, the fractal dimension of cracks is further increased, and the loading time lasts 60 μs. The fractal dimension increased by 0.06 from 1.32 to 1.38, indicating a growth rate of 0.001. The fractal dimension increases rapidly in the crack propagation stage, and slowly increases in crack widening stage. This inflection point shows that the fractal dimension conveys relevant information about the state of the cracks in a sample. Figure 8 shows similar diagrams of the fractal dimension of the samples under impact loading of 101 and 166 GPa/s.

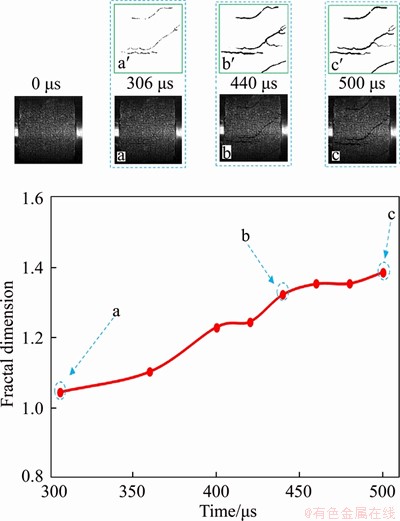
Figure 7 Change in fractal dimension over time for a sample loaded at 279 GPa/s

The calculated fractal dimensions of crack patterns in images of coal under different loading rates are plotted in Figure 8. The fractal dimensions of all the crack patterns increase over the course of the test. The fractal dimension of the crack patterns clearly changes in stages at each loading rate. The fractal dimension increases rapidly in the first stage of crack propagation (crack propagation stage). The fractal dimension then increases slowly in the second stage, while the cracks widen (crack widening stage). This distinction in the behavior of the fractal dimension means that this calculation can be used to characterize the state of cracks in a sample of coal.

Figure 8 Fractal dimension of cracks formed by dynamic compression using different loading rates

Figure 8 also shows that the fractal dimension is higher at a given time if the loading rate is faster. As the loading rate increases, the sample is subjected to a stronger dynamic impact, so more cracks form on the surface, and the fractal dimension is accordingly higher. In the crack propagation stage, new cracks form and propagate throughout the sample, increasing the complexity of the crack pattern and quickly increasing the fractal dimension. In the crack widening stage, the increasing width of the cracks does not greatly affect the fractal dimension. Even so, the fractal dimension is positively correlated with the loading rate, so it can be used to characterize the state of a rock sample that has been subjected to a dynamic load.

4 Discussion

4.1 Mechanism driving cracking under dynamic compressive loading

This section analyzes the strain field of the sample tested at the loading rate of 279 GPa/s as an example to reveal the mechanism by which the cracks change over time.

The strains shown in Figure 9 are composed of the two following parts: the strain caused by the deformation of the coal sample after the impact load is applied and the observed displacement caused by translation and rotation of the sample. Since x direction is aligned with the incident bar, the sample will be displaced in the x direction, so the observed strain should change the most in this direction. Therefore, the following analysis will focus on x direction strain.

As shown in Figure 9, at the beginning of loading, the strain regions in x and y direction strain diagrams of the sample are scattered, with the maximum strain values of 0.0035 and 0.0014, respectively, indicating that multiple reflections of the incident wave reach dynamic stress equilibrium. As dynamic compression progresses, the internal strain of the sample increases gradually. At 160 μs after the beginning of the impact load, the internal stress distribution of the sample changes from diffuse to striped. The maximum strain value increases to 0.0114 at this moment. As the compression test progresses, strain concentrations appear in many places on the sample surface. At 306 μs, the strain of the sample increases somewhat, but individual areas of strain in the x and y directions are missing due to the spot mismatch phenomenon, which is caused by some of the speckle pattern being destroyed by the surface cracks. This moment corresponds to the beginning of the crack widening stage. At 320 μs, even more of the speckled are lost to the crack evolution. The above analysis shows that the dynamic evolution of crack patterns intensifies over the course of impact loading such that stress concentrations form throughout the sample, ultimately resulting in splitting failure [35].

Figure 9 Strain fields of coal sample in x and y directions at σ=279 GPa/s:

Coal-rock contains many defects, such as microcracks and holes. Under the effect of an external load, microcracks gradually form in the rock and eventually expand until macrofractures appear. Related research shows that the internal properties of rock materials deteriorate due to the concentration of local tensile stress in the material at the microscopic scale [36]. Figure 9 shows that as the loading progresses, the stress field changes because of the distribution of microcracks in the sample, and a local tensile stress concentration forms before the sample begins to crack. According to the Mohr-Coulomb criterion [37], when an impact load is applied, the rock will fail once the shear stress on a plane in the rock exceeds that plane’s shear stress threshold.

4.2 Influence of loading rate on coal sample crushing

The dynamic compressive properties of coal- rock materials are important parameters for studying the transfer of dynamic loads in coal and rock masses and the response of coal and rock mass structures under dynamic loading. Figure 10 shows the dynamic compressive strengths of the coal samples under uniaxial loading with different loading rates. Figure 10 shows that during the loading rate range of 100-700 GPa/s, the coal samples exhibit a strong loading rate effect. As the loading rate increases, the dynamic compressive strength exhibits a non-linear increase: the rate of increase in the dynamic compressive strength of the coal samples gradually decreases. The exponential function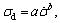where σ_d is the loading rate of coal samples; is the coal sample loading rate; and a and b are fitting constants and are used for fitting, and the fitting effect is good. This finding is consistent with results in Ref. [38] on the dynamic compressive strength of sandstone under different loading rates. The form of the fitting function of the relationship between the dynamic compressive strength and strain rate is consistent. Because the strength of sandstone is higher than that of coal, the values of a and b will also be different for sandstone and coal.

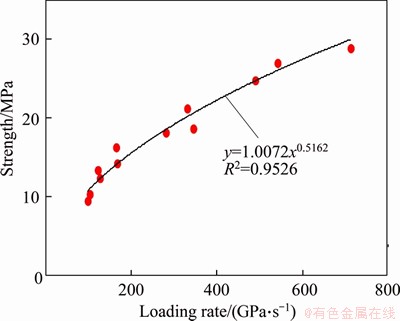
Figure 10 Uniaxial dynamic compressive strength of coal under different loading rates

Affected by the geological conditions during the formation and accumulation of the coal body, it contains a large number of microcracks, joints and pores. These defects will have a greater impact on the state of the coal body after the coal is stressed. The process of coal destruction under force will be accompanied by the generation and expansion of cracks, leading to the final destruction by cracks. The number of cracks in the coal body increases as the loading rate increases, and the corresponding energy demand also increases. Since the impact load time is often extremely short, the sample does not have enough time for energy accumulation. According to the functional principle, the sample can balance external energy only by increasing stress, and the dynamic compressive strength of the sample will vary as the loading rate increases [38].

The coal will rupture once the impact load exceeds the compressive strength of the coal. Examining the rupture state and final failure mode of coal during the impact process can deepen our understanding of the mechanisms driving rupture, instability, and fracture development in coal. The fractal dimension of coal-rock fissures is clearly affected by the loading rate, and higher loading rates yield cracks with higher fractal dimensions. As time elapses during an impact load, the fractal dimension begins to change less rapidly once the cracks start to widen. Our analysis above shows that the fractal dimension of a crack pattern is correlated with the loading rate and that crack patterns with higher fractal dimensions caused by stronger external loads will cause the rock to fail into smaller pieces. Figure 11 shows raw images of the failed coal samples under different loading rates. The resulting blocks are smaller when the sample is subjected to a faster loading rate.

Figure 11 Failure patterns of coal samples under different loading rates during dynamic compression (unit: GPa/s)

The fractal dimension of the cracks in a coal mass subjected to an impact load can be used to quantitatively characterize the degree of coal damage during the impact load. The complexity of the surface crack patterns is directly related to the manner in which the coal samples finally fracture. According to Figure 11, when the loading rate is relatively slow, the samples break into larger fragments at failure. As the loading rate increases, the degree of fragmentation increases, fewer large fragments remain, and the smallest particles are dust-sized particles. When the loading rate is 543 GPa/s, the samples break into powder-sized particles due to such a strong impact load. At faster loading rates, therefore, the samples are essentially pulverized. This difference in the coal behavior shows that the samples absorb more energy before fracturing at faster loading rates, such that a greater number of cracks form within the rock mass. For instance, LIU et al [39] studied the correlation between the fractal dimension of crack patterns and the degree of crushing, and their results agree with ours. Therefore, the type of failure of a coal-rock mass is reflected in the increase in the fractal dimension of surface cracks during loading. Therefore, the fractal dimension of surface cracks can be used to predict the failure state of a rock mass subjected to dynamic loads.

5 Conclusions

In this paper, a method combining SHPB and DIC is used to record and analyze the dynamic compressive failure process of coal samples, and the resulting cracks are extracted from images captured by high-speed photography through image processing. The box fractal dimension is used to analyze the crack evolution under dynamic loading. A quantitative description shows that the dynamic changes in the fractal dimension of the cracks in the coal sample under impact loading with different loading rates are obtained, indicating that the fractal dimension can effectively characterize the evolution of coal-rock cracks under dynamic loading. The main conclusions are as follows:

1) The fractal dimension of crack patterns increases in a consistent trend as the loading time elapses, indicating that the fractal dimension can be used to quantitatively represent the progression of coal failure under dynamic loading.

2) During dynamic loading, cracks mainly form along the axis of the load, and the cracks progress in two distinct phases. During the crack propagation phase, the fractal dimension increases rapidly as cracks initially form in complex patterns. During the crack widening stage, the fractal dimension increases more slowly as the crack widths increase.

3) Cracks propagate after widening. The crack propagation phase begins earlier (the initial cracks form earlier) in the compression process at faster loading rates.

4) Considering the same elapsed time since the beginning of dynamic loading, the fractal dimension is higher when the loading rate is faster. This result indicates that the loading rate, not just the magnitude of the load, has a direct effect on the development of fractures in coal.

5) There is clearly a loading rate effect on the dynamic compressive strength of the coal samples. With the increase in the loading rate, the dynamic compressive strength of the coal samples gradually increases. The relationship between the dynamic compressive strength and the loading rate can be assumed to be an exponential function(R²=0.9526) to achieve an effective fitting.

Contributors

The overarching research goals were developed by GAO Ming-zhong, LI Sheng-wei and CUI Peng-fei. ZHANG Jian-guo, WANG Man and WANG Ying-wei are responsible for on-site sampling and lithology analysis. GAO Ming-zhong, CUI Peng-fei, ZHANG Jian-guo and LI Sheng-wei analyzed the calculated results. The initial draft of the manuscript was written by GAO Ming-zhong and CUI Peng-fei. All authors replied to reviewers’ comments and revised the final version.

Conflict of interest

GAO Ming-zhong, ZHANG Jian-guo, LI Sheng-wei, WANG Man, WANG Ying-wei and CUI Peng-fei declare that they have no conflict of interest.

References

[1] MANDELBROT B B. The fractal geometry of nature [M]. New York: W H Freeman, 1982.

[2] CAMPBELL P, ABHYANKAR S. Fractals form chance and dimension [J]. Mathematical Intelligencer, 1978, 1(1): 35-37. DOI: 10.1007/BF03023043.

[3] XIE He-ping. Fractal kinematics of crack propagation in geomaterials [J]. Journal of China University of Mining & Technology, 1995, 5(1): 1-8. DOI: 10.1016/0013-7944(94) 00203-T. (in Chinese)

[4] JIANG Yao-dong, PAN Yi-shan, JIANG Fu-xing, DOU Lin-ming, JU Yang. State of the art review on mechanism and prevention of coal bumps in China [J]. Journal of China Coal Society, 2014, 39(2): 205-213. DOI: 10.13225/j.cnki. jccs.2013.0024. (in Chinese)

[5] DOU Lin-ming, JIANG Yao-dong, CAO An-ye, LIU Hai-shun, GONG Si-yuan, CAI Wu, ZHU Guang-an. Monitoring and pre-warning of rockburst hazard with technology of stress field and wave field in underground coalmines [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(4): 803-811. DOI: 10.13722/j.cnki. jrme.2016.0756. (in Chinese)

[6] AHAMED M A A, PERERA M S A, LI Dong-yin, RANJITH P G, MATTHAI S K. Proppant damage mechanisms in coal seam reservoirs during the hydraulic fracturing process: A review [J]. Fuel, 2019, 253: 615-629. DOI: 10.1016/j.fuel.2019.04.166.

[7] KIYAMA T, NISHIMOTO S, FUJIOKA M, XUE Zi-qiu, ISHIJIMA Y, PAN Zhe-jun, CONNELL D L. Coal swelling strain and permeability change with injecting liquid/supercritical CO₂ and N₂ at stress- constrained conditions [J]. International Journal of Coal Geology, 2011, 85(1): 56-64. DOI: 10.1016/j.coal.2010.09. 010.

[8] XU Jiang, SU Xiao-peng, CHENG Li-chao, WANG Lei, LIU Jing, FENG Dan. Evolution characteristics of meso-crack of gas-filled raw coal under compression-shear stress [J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(3): 458-467. DOI: 10.3969/j.issn.1000-6915.2014.03. 002. (in Chinese)

[9] ZHAO Yi-xin, LIU Shi-min, ZHAO Gao-feng, DEREK E, JIANG Yao-dong, HAN Jing-li. Failure mechanisms in coal: Dependence on strain rate and microstructure [J]. Journal of Geophysical Research Solid Earth, 2015, 119(9): 6924-6935. DOI: 10.1002/2014JB0 11198.

[10] LI Zhen-tao, LIU Da-meng, CAI Yi-dong, RANJITH P G, YAO Yan-bin. Multi-scale quantitative characterization of 3-D pore-fracture networks in bituminous and anthracite coals using FIB-SEM tomography and X-ray μ-CT [J]. Fuel, 2017, 209: 43-53. DOI: 10.1016/j.fuel.2017.07.088.

[11] GONG Feng-qiang, YE Hao, LUO Yong. Rate effect on the burst tendency of coal-rock combined body under low loading rate range [J]. Journal of China Coal Society, 2017, 42(11): 2852-2860. DOI: 10.13225/j.cnki.jccs.2017.0159. (in Chinese)

[12] GONG Feng-qiang, SI Xue-feng, LI Xi-bing, WANG Shan-yong. Dynamic triaxial compression tests on sandstone at high strain rates and low confining pressures with split Hopkinson pressure bar [J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 113: 211-219. DOI: 10.1016/j.ijrmms.2018.12.005.

[13] GONG Feng-qiang, ZHAO Gao-feng. Dynamic indirect tensile strength of sandstone under different loading rates [J]. Rock Mechanics & Rock Engineering, 2013, 47(6): 2271-2278. DOI: 10.1007/s00603-013-0503-7.

[14] KLEPACZKO J R, BASSIM M N, HSU T. Fracture toughness of coal under quasi-static and impact loading [J]. Engineering Fracture Mechanics, 1984, 19(2): 305-316. DOI: 10.1016/0013-7944(84)90025-0.

[15] ZIPF R K, BIENIAWSKI Z T. Mixed-mode fracture toughness testing of coal [J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1990, 27(6): 479-493. DOI: 10.1016/0148-9062(90)910 00-W.

[16] SHAN Ren-liang, CHENG Rui-qiang, GAO Wen-jiao. Study on dynamic constitutive model of anthracite of Yunjialing coal mine [J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(11): 2258-2263. DOI: 10.1016/ S1872-1508(06)60035-1. (in Chinese)

[17] LUNDBERG B. A split Hopkinson bar study of energy absorption in dynamic rock fragmentation [J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1976, 13(6): 187-197. DOI: 10.1016/0148-9062(76)91285-7.

[18] ZHAO Yi-xin, GONG Shuang, ZHANG Cheng-guo, ZHANG Zhen-nan, JIANG Yao-dong. Fractals characteristics of crack propagation in coal under impact loading [J]. Fractals-complex Geometry Patterns & Scaling in Nature & Society, 2018, 26(2): 1840014. DOI: 10.1142/S021834 8X18400145.

[19] ZHAO Yi-xin, GONG Shuang, HAO Xian-jie, PENG Yan, JIANG Yao-dong. Effects of loading rate and bedding on the dynamic fracture toughness of coal: Laboratory experiments [J]. Engineering Fracture Mechanics, 2017, 178: 375-391. DOI: 10.1016/j.engfracmech.2017.03.011.

[20] XIA K W, ARES J R, HIROO K, JAMES R R. Laboratory earthquakes along inhomogeneous faults: Directionality and supershear [J]. Science, 2005, 308(5722): 681-684. DOI: 10.1126/science.1108193.

[21] XIA K W, ARES J R, HIROO K, JAMES R R. Laboratory earthquakes: The sub-Rayleigh-to-supershear rupture transition [J]. Science, 2004, 303(5665): 1859-1861. DOI: 10.1126/science.1094022.

[22] ZHANG Xi-hong, HAO Hong, MA Guo-wei. Laboratory test and numerical simulation of laminated glass window vulnerability to debris impact [J]. International Journal of Impact, 2013, 55: 49-62. DOI: 10.1016/j.ijimpeng.2013. 01.002.

[23] ZHANG Xi-hong, HAO Hong, MA Guo-wei. Dynamic material model of annealed soda-lime glass [J]. International Journal of Impact, 2015, 77: 108-119. DOI: 10.1016/ j.ijimpeng.2014.11.016.

[24] ZHAO Hong-bao, WANG Zhong-wei, ZHANG Huan, LI Wei. Effects of dynamic loads on development of internal microstructure and distribution of new surface fractures of coal [J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(5): 971-979. DOI: 10.13722/j.cnki. jrme.2015.1541. (in Chinese)

[25] HAN Xiu-hui, LI Cheng-wu, XING Tong-zhen, GAO Ping-bo. Experimental study on coal impact fracturing based on temporal and spatial evolution of deformation field [J]. Journal of China Coal Society, 2016, 41(11): 2743-2755. DOI: 10.13225/j.cnki.jccs.2015.1984. (in Chinese)

[26] LIU Xiao-hui, DAI Feng, LIU Jian-feng, ZHANG Ru. Brazilian splitting tests on coal rock considering bedding direction under static and dynamic loading rate [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 10: 2098-2105. DOI: 10.13722/j.cnki.jrme.2015.0608. (in Chinese)

[27] AI Di-hao, ZHAO Yue-chao, WANG Qi-fei, LI Cheng-wu. Experimental and numerical investigation of crack propagation and dynamic properties of rock in SHPB indirect tension test [J]. International Journal of Impact Engineering, 2019, 126(2019): 135-146. DOI: 10.1016/j.ijimpeng.2019. 01.001.

[28] XIE He-ping. Fractal: An introduction to rock mechanics [M]. Beijing: Science Press,1996.

[29] MANDELBROT B B. How long is the coast of Britain? statistical self-similarity and fractional dimension [J]. Science, 1967, 156(3775): 636-638. DOI: 10.1126/science. 156.3775.636.

[30] ROLPH S. Fractal geometry: Mathematical foundations and applications [J]. Mathematical Gazette, 1990, 74(469): 288-317. DOI: 10.2307/3619861.

[31] XING H Z, ZHANG Q B, BRATHWAITE C H, PAN B, ZHAO J. High-speed photography and digital optical measurement techniques for geomaterials: Fundamentals and applications [J]. Rock Mechanics & Rock Engineering, 2017, 50(6): 1611-1659. DOI: 10.1007/s00603-016-1164-0.

[32] HUANG Sheng, XIA Kai-wen, YAN Fei, FENG Xia-ting. An experimental study of the rate dependence of tensile strength softening of long you sandstone [J]. Rock Mechanics & Rock Engineering, 2010, 43(6): 677-683. DOI: 10.1007/s00603-010-0083-8.

[33] DAI Feng, HUANG Sheng, XIA Kai-wen, TAN Zhuo-ying. Some fundamental issues in dynamic compression and tension tests of rocks using split Hopkinson pressure bar [J]. Rock Mechanics & Rock Engineering, 2010, 43(6): 657-666. DOI: 10.1007/s00603-010-0091-8.

[34] XIA Kai-wen, YAO Wei, WU Bang-biao. Dynamic rock tensile strengths of Laurentian granite: Experimental observation and micromechanical model [J]. Journal of Rock Mechanics & Geotechnical, 2017, 9(1): 116-124. DOI: 10.1016/j.jrmge.2016.08.007.

[35] XU Peng, YANG Ren-shu, JU Yang, XIA Kai-wen, GUO Yang. Experimental study on influences of inclined weak interface on the dynamic crack propagation behavior [J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1645-1652. DOI: 10.11779/CJGE201909008. (in Chinese)

[36] GRADY D, KIPP M E. Continuum modelling of explosive fracture in oil shale [J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1980, 17(3): 147-157. DOI: 10.1016/0148-9062(80)9136 1-3.

[37] NICK B. Non-linear shear strength for rock, rock joints, rockfill and interfaces [J] Innovative Infrastructure Solutions, 2016, 30: 2370. DOI: 10.1007/s41062-016- 0011-1.

[38] GONG Feng-qiang, LU Dao-hui, LI Xi-bing, RAO Qiu-hua. Experimental research of sandstone dynamic strength criterion under different strain rates [J]. Rock and Soil Mechanics, 2013, 34(9): 2433-2441. DOI: 10.16285/j.rsm. 2013.9.007. (in Chinese)

[39] LIU Xiao-hui, ZHANG Ru, LIU Jian-feng. Dynamic test study of coal rock under different strain rates [J]. Journal of China Coal Society, 2012, 37(9): 1528-1534. DOI: 10.1007/ s11783-011-0280-z. (in Chinese)

(Edited by ZHENG Yu-tong)

中文导读

动态加载率对深部岩石破坏过程裂隙分形维数的影响

摘要：本文采用高速摄像与数字散斑法相结合的方法记录煤样动态破坏过程，并通过图像处理对高速摄影捕捉到的试样图片进行裂隙提取，采用盒分形维数定量描述煤样裂隙，得到了不同加载率冲击载荷下煤样动态裂隙的分形维数变化特性。结果表明，分形方法可以有效地定量描述动载荷作用下煤样裂隙演化过程。在动态加载过程中，煤体裂隙演化呈现明显的阶段性；在裂隙扩展阶段，分形维数随着加载的进行迅速增大；在裂隙宽度增加阶段，分形维数随着加载的进行缓慢增大；在动态加载过程中，煤样裂隙扩展阶段时间随着加载率的增大而逐渐延长，随着加载率的增大，裂纹初始产生时间提早；在相同的加载时间内，分形维数随着加载率的增大而逐渐增大。

关键词：分形；加载率；冲击载荷；煤裂隙

Foundation item: Projects(51822403, 51827901) supported by the National Natural Science Foundation of China; Project(2019ZT08G315) supported by the Department of Science and Technology of Guangdong Province, China

Received date: 2020-06-10; Accepted date: 2020-09-17

Corresponding author: CUI Peng-fei, PhD Candidate; Tel: +86-15565617893; E-mail: cpf6134@163.com; ORCID: https://orcid.org/ 0000-0002-9868-2403