钢-混凝土组合梁负弯矩区弹性畸变屈曲分析
周旺保1,蒋丽忠1,2,邵光强1,余志武1,2
(1. 中南大学土木建筑学院,湖南 长沙,410075;
2. 高速铁路建造技术国家工程实验室,湖南 长沙,410075)
摘要:基于畸变屈曲是钢-混凝土组合梁负弯矩区钢梁的重要屈曲模式,钢梁下翼缘提供给钢梁腹板的转动约束刚度及侧向约束刚度是影响其畸变屈曲性能的关键因素之一,对工字形钢-混凝土组合梁负弯矩区钢梁腹板提供给下翼缘的转动约束刚度及侧向约束刚度进行研究。采用利用能量法推导负弯矩区钢梁腹板对下翼缘的转动约束刚度及侧向约束刚度理论计算公式,并结合弹性介质中的中心受压薄壁杆件的屈曲理论推导钢梁侧向弯曲屈曲及侧向弯扭屈曲临界应力计算公式,进一步获得相应的屈曲弯矩。结合工程实例对转动约束刚度、侧向约束刚度及屈曲弯矩计算公式进行分析及讨论。研究结果表明:钢梁腹板转动约束刚度及侧向约束刚度均与外荷载呈线性关系,同时两者还可能出现负值;本文屈曲弯矩计算结果与ANSYS有限元计算结果较吻合;现有屈曲弯矩计算方法存在一定理论缺陷,且不同计算方法所得计算结果偏差较大;本文计算公式形式较简洁,适于工程应用。
关键词:钢-混凝土组合梁;畸变屈曲;转动约束刚度;侧向约束刚度;临界弯矩;负弯矩
中图分类号:TU398.9;TU312;TU973+.2 文献标志码:A 文章编号:1672-7207(2012)06-2316-08
Elastic distortional buckling analysis of steel-concrete composite beams in negative moment region
ZHOU Wang-bao1, JIANG Li-zhong1,2, SHAO Guang-qiang1, YU Zhi-wu1,2
(1. School of Civil and Architectural Engineering, Central South University, Changsha 410075, China;
2. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China)
Abstract: Based on the fact that distortional buckling is one of the important buckling modes for steel-concrete composite beams in the negative moment region, and the distortional buckling load depends significantly on the rotational restraint stiffness and lateral restraint stiffness provided by the lower cloud point flange to the steel beam web plate during buckling deformation, the rotational restraint stiffness and lateral restraint stiffness were presented. Based on the energy method, the analytical expressions for the rotational restraint stiffness and lateral restraint stiffness were derived, and combining the thin-walled bar buckling theory in elastic medium, the lateral bending buckling stress and lateral flexural-torsional buckling stress calculation and the corresponding critical moment formulas were derived. The results show that the rotational restraint stiffness and lateral restraint stiffness has linear relationship with external loads, both can be negative, the calculation results of this paper agree well with the ANSYS analysis results, and the deviation of the calculation results in existing computing methods that have some theory shortcomings is great. The analytical expressions is relatively more concise, and so it is suitable for engineering application.
Key words: steel-concrete composite beams; distortional buckling; rotational restraint stiffness; lateral restraint stiffness; critical moment; negative moment
钢-混凝土组合梁由型钢或焊接工字钢通过抗剪连接件与混凝土形成整体共同承受外部荷载的作用。由于这种结构能充分发挥钢材受拉、混凝土抗压, 使结构具有承载力高、塑性和韧性好、施工方便、经济效果显著的优势, 在大跨度桥梁和高层建筑中得到广泛应用。在实际结构中, 因为混凝土翼缘板的抗弯、抗扭刚度很大, 同时,由于混凝土板通过栓钉与工字钢梁上翼缘紧密地连成一体,所以,对于组合梁正弯矩区不存在侧向失稳验算问题。但在组合梁的负弯矩区域,钢梁下翼缘在承受较大的可变荷载以及不利荷载分布时,呈受压状态而产生侧向失稳,并伴随钢梁腹板的横向变形,很容易出现畸变屈曲的现象。但是,在我国现行钢结构设计规范[1]中没有组合梁稳定设计的内容,工程界基本沿袭非约束工字钢梁的稳定设计方法或者采用弹性地基梁上非变轴力压杆稳定求解方法。这些方法既不统一,结果也过于保守。目前,钢-混组合梁方面的研究很多[1-10],但涉及组合梁负弯矩区的畸变屈曲方面的研究还很少。文献[5-11]等对薄壁钢梁畸变屈曲方面进行了理论分析与试验研究,但鉴于组合梁和薄壁钢梁受力特性的差异,不能照搬钢梁理论,因此,有必要对组合梁畸变屈曲进行相关的理论分析和试验研究。文献[12-16]利用能量法对工形钢-混凝土组合梁及钢-混凝土箱梁的畸变屈曲进行了理论分析,但利用能量法分析时不能清晰地反映腹板对下翼缘约束作用及腹板约束对屈曲荷载的影响,从而不能将侧向弯曲失稳与侧向弯扭失稳进行统一分析,物理概念不清晰。同时,文献[16]与文献[13-15]不同的是考虑了整个截面的圣维南扭转,未考虑到屈曲波长,导致计算结果有一定偏差。文献[21]中所介绍的弹性地基梁法中没有考虑到负弯矩区混凝土已大部分开裂并退出工作,利用条元法求解转动约束刚度计算公式时未考虑到相邻条元的约束作用,同时,未考虑到腹板对翼缘具有转动约束作用,从而导致计算结果有一定偏差。可见,有必要对组合梁中钢梁腹板对下翼缘的转动约束刚度、侧向约束刚度及相应的畸变屈曲荷载进行更深入研究。为此,本文作者在合理假设基础上,利用能量法[17-18]获得工形钢-混凝土组合梁中钢梁下翼缘在纵向线性分布应力作用下对钢梁腹板的转动约束刚度kf及侧向约束刚度kx的计算公式,对kf与kx的特性进行分析,并在此基础上,利用弹性介质中中心受压薄壁杆件的屈曲理论[19-20]计算工形钢-混凝土组合梁负弯矩区的侧向弯曲屈曲应力及侧向弯扭屈曲应力,并进一步获得相应的屈曲弯矩。最后结合实例将本文计算方法与文献[16,21]中计算方法及ANSYS有限元方法进行比较,以验证本文计算方法的正确性。
1 基本假定
钢-混凝土组合梁基本尺寸见图1,组合梁中的工字钢梁与自由的简支钢梁(非约束钢梁)的侧向失稳模式不同,它的上翼缘嵌固在刚度较大的混凝土翼缘板上,侧向变形和扭转变形都受到了一定程度的约束;它的下翼缘受压,虽然有可能产生侧向位移和扭转角,但是受到腹板的侧向约束,因此,组合梁的侧向失稳可以定义为伴随钢梁腹板侧向受弯变形的畸变屈曲。钢-混凝土组合梁与普通钢梁在负弯矩作用下屈曲特性的基本区别见图2。从图2可以看出:钢-混凝土组合梁负弯矩区钢梁屈曲属于畸变屈曲。

图1 钢-混凝土组合梁截面尺寸及坐标
Fig.1 Cross-section dimensions of steel-concrete composite beams and axes
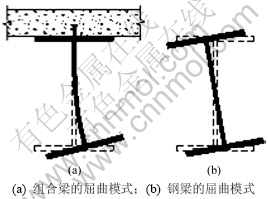
图2 钢-混凝土组合梁与普通钢梁屈曲特性
Fig.2 Buckling behavior of steel-concrete composite beams and plain steel beams
采用固定的右手坐标系xyz,坐标原点O为工字钢下翼缘的形心。如图1 所示单轴对称截面的受弯组合梁, 在其刚度较大的yz平面内承受着弯矩Mx。为了计算方便,在分析计算钢梁下翼缘对钢梁腹板的转动约束刚度kφ、侧向约束刚度kx及相应屈曲弯矩时, 还需要进行如下假定:
(1) 材料是各向同性的完全弹性体;
(2) 构件为等截面梁而且无初始缺陷;
(3) 在畸变屈曲时钢梁下翼缘截面形状保持 不变;
(4) 钢筋混凝土翼板的刚度很大,钢梁上翼缘由于受到混凝土翼板的约束不能发生侧向变形和扭转 变形;
(5) 在负弯矩作用下组合梁屈曲时混凝土已大部分开裂,忽略混凝土的抗弯作用,只考虑混凝土翼板中钢筋的抗弯作用;
(6) 腹板对下翼缘的竖向约束刚度ky=∞。
根据上述基本假定,钢-混凝土组合梁畸变屈曲模型可简化为下翼缘在水平方向和扭转方向受弹簧约束及竖向受刚性约束的薄壁约束扭转问题,其简化计算模型如图3所示。

图3 钢-混凝土组合梁简化计算模型
Fig.3 Simplified calculation model of steel-concrete composite beams
2 腹板约束系数kf与kx的确定及分析
2.1 转动约束刚度kf的确定
如图4所示,取1个半波长的腹板板段为研究对象。板段的长、宽和厚度分别为λ,hw和tw,λ为畸变屈曲在构件纵向形成的1个半波的长度(以下简称半波长度);两横向对边简支,与上翼缘交接边固支,与下翼缘交接边简支。其中两简支对边承受沿z方向的纵向线性分布应力σ (压应力为正,拉应力为负),与下翼缘交接边承受下翼缘对腹板的等效弹簧约束弯矩m(z)。设组合梁全截面钢材重心纵坐标为-yc,全截面钢材绕其重心的惯性矩为I。根据上述假设可知:在负弯矩作用下考虑混凝土板翼缘钢筋后,腹板下边缘处轴向压应力为σ1=Mxyc/I;腹板上边缘处轴向外压应力σ2=σ1(yc-hw)/yc;腹板其他点所承受的轴向外压应力为σ=σ1(yc+y)/yc,其中Mx为作用在组合梁上的负弯矩。

图4 承受分布压应力及分布弯矩的腹板
Fig.4 Rectangular plate subjected to compression and moments
根据上述分析,取纵向1个半波长λ为研究对象,设 (其中,μ为钢材泊松比,E为钢材弹性模量),并设u为腹板变形函数,其边界条件可表示为:
(其中,μ为钢材泊松比,E为钢材弹性模量),并设u为腹板变形函数,其边界条件可表示为:
 (1a)
(1a)
 (1b)
(1b)
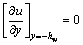 (1c)
(1c)
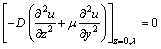 (1d)
(1d)
根据上述边界条件,可取位移函数为:
 (2)
(2)
代入边界条件得:
c1=c+c2 (3a)
2c1=c+3c2 (3b)
由式(3a)和(3b)得:
c1=2c,c2=c (4)
将式(4)代入式(2)得:
 (5)
(5)
由文献[16-17]可知半波长腹板在小变形情况下的应变能为:

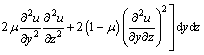 (6)
(6)
将式(5)代入式(6)得:
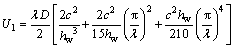 (7)
(7)
半波长纵边弹簧约束引起的弹性势能为:
 (8)
(8)
将式(5)代入式(8)得:
 (9)
(9)
利用材料力学外力功的计算公式可得半波长腹板上的外力功[17-18]为:
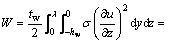
 (10)
(10)
将式(5)代入式(10)得:
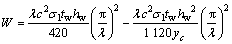 (11)
(11)
半波长腹板总势能为:
 (12)
(12)
将式(7),(9)和(11)代入式(12)得:
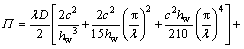
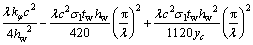 (13)
(13)
由势能驻值原理可得:

 (14)
(14)
求解式(14)得:

 (15)
(15)
2.2 侧向约束刚度kx的确定
仍取1个半波长的腹板板段为研究对象,如图5所示。板段两横向对边简支,与上翼缘交接边固支,与下翼缘交接边可侧向移动。其中两简支对边承受沿z方向的纵向线性分布应力σ(压应力为正,拉应力为负),与下翼缘交接边承受下翼缘对腹板的等效弹簧约束分布力f(z)。

图5 承受分布压应力及分布侧向应力的腹板
Fig.5 Rectangular plate subjected to compression and lateral stress
根据上述分析,其边界条件可表示为:
 (16a)
(16a)
 (16b)
(16b)
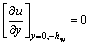 (16c)
(16c)
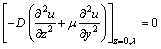 (16d)
(16d)
根据上述边界条件,可取位移函数为:
 (17)
(17)
代入边界条件可得:
c1=0,c2=-3c,c3=-2c (18)
将式(18)代入式(17)得:
 (19)
(19)
将式(19)代入式(6)得半波长腹板在小变形情况下的应变能U1为:
 (20)
(20)
半波长纵边弹簧约束引起的弹性势能U2为:
 (21)
(21)
将式(19)代入式(21)得:
 (22)
(22)
将式(19)代入式(10)得半波长腹板上的外力功W为:
 (23)
(23)
将式(20),(22)和(23)代入式(12)得半波长腹板总势能 为:
为:
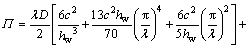
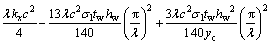 (24)
(24)
由势能驻值原理得:

 (25)
(25)
求解式(25)得:
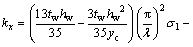
 (26)
(26)
2.3 关于kx与kφ的讨论
(1) 从式(15)及式(26)可以看出:转动约束刚度kf及侧向约束刚度kx均与下翼缘纵向压应力σ1呈线性关系,因为在一般情况下,hw/yc<2,所以,σ1前系数为正,即σ1越大,钢梁下翼缘对腹板的转动约束刚度与侧向约束刚度越大。同时也说明钢梁下翼缘对腹板的转动约束刚度及侧向约束刚度均与压应力σ1有关,而不是由组合梁截面自身特性决定的。
(2) 式(15)和式(26)等号右边多项式中均出现了负号项,说明转动约束刚度及侧向约束刚度均有可能为负值。这与常规刚度及刚度矩阵均为正定是不同的。如转动约束刚度或侧向约束刚度为负值,钢梁下翼缘会受到腹板的转动或侧向约束,即钢梁腹板会减缓下翼缘屈曲而钢梁下翼缘则会促进腹板屈曲。文献[21]中所描述的弹性约束压杆失稳模型中利用条元法求出侧向约束刚度k的计算公式为 ,但该方法未考虑到相邻条元的约束作用,故该计算公式所获得的侧向约束刚度k与外荷载无关且始终为正,这与实际情况不符,同时未考虑到转动约束刚度,这样便导致组合梁屈曲荷载计算结果存在一定误差。
,但该方法未考虑到相邻条元的约束作用,故该计算公式所获得的侧向约束刚度k与外荷载无关且始终为正,这与实际情况不符,同时未考虑到转动约束刚度,这样便导致组合梁屈曲荷载计算结果存在一定误差。
(3) 式(26)与式(15)等号右侧对应第1项、第2项及第3项的比值分别为:
 (27)
(27)
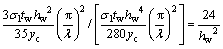 (28)
(28)
 (29)
(29)
从式(27),(28)和(29)可知: 是不为无穷小的数,也不是
是不为无穷小的数,也不是 。因此,下翼缘对腹板的侧向约束刚度不可以忽略的,即在计算过程中不能取kx=0,从而从理论上论证了工形钢-混凝土组合梁构件中下翼缘对腹板侧向约束刚度不能近似为0,这与文献[7,10]中指出的冷弯薄壁卷边槽钢腹板对上下翼缘侧向约束刚度为0的观点不同。
。因此,下翼缘对腹板的侧向约束刚度不可以忽略的,即在计算过程中不能取kx=0,从而从理论上论证了工形钢-混凝土组合梁构件中下翼缘对腹板侧向约束刚度不能近似为0,这与文献[7,10]中指出的冷弯薄壁卷边槽钢腹板对上下翼缘侧向约束刚度为0的观点不同。
2.4 工程实例分析
某多跨连续工字形组合梁的截面尺寸如图6所示。若组合梁负弯矩跨受纯弯矩作用,计算钢梁下翼缘对腹板的转动约束刚度及侧向约束刚度,不考虑残余应力的影响。其中组合梁的工字钢为I20a, 混凝土翼板为C40现浇混凝土板,混凝土板厚h=120 mm,有效宽度bc=800 mm,负弯矩跨度l=4 m。
(1) 截面的几何性质:hw=188.6 mm,tf=11.4 mm,bf=100 mm,tw=7 mm,yc=175.63 mm,I=80 847 418.2 mm4。

图6 组合梁横截面尺寸
Fig.6 Cross-section dimensions of steel-concrete composite beams
(2) 材料特性:弹性模量E=2.06×105 N/mm2,剪切模量G=0.79×105 N/mm2,泊松比μ=0.3。
对于半波长的取值及失稳弯矩的取值将在后续篇介绍。本文暂参考文献[13]取半波数为4,则半波长λ= 1 000 mm。
(1) 取屈曲弯矩为Mcr=5.95×108 N·mm,则有:
σ1=Myc/I=1 299 N/mm2 (30)
将上述参数分别代入式(15)和(26)得:
kφ=2.64σ1-0.141E=-0.256×105 N (31)
kx=3.63×10-3σ1-5.68×10-6E=3.55 N/mm2 (32)
(2) 取屈曲弯矩为Mcr=5.95×109 N·mm,则
σ1=Myc/I=12 990 N/mm2 (33)
将上述参数分别代入式(15)和(26)得:
kφ=2.63σ1-0.141E=0.512×104 N (34)
kx=3.63×10-3σ1-5.68×10-6E=46 N/mm2 (35)
(3) 取屈曲弯矩为Mcr=5.95×107 N·mm,则
σ1=Myc/I=12 990 N/mm2 (36)
将上述参数分别代入式(15)和(26)得:
kφ=2.63σ1-0.141E=-0.287×105 N (37)
kx=3.63×10-3σ1-5.68×10-6E=-0.699 N/mm2 (38)
由式(30)~(38)可知:当外荷载不同时,钢梁下翼缘的转动约束刚度及侧向约束刚度可取正值及负值,当外荷载特定时甚至可取0。下翼缘转动及侧向约束刚度可以为负值,这与常规刚度及刚度矩阵均为正定的观点是不同的,从而可以加深对刚度的理解。
3 临界弯矩的理论推导
3.1 临界弯矩的推导
如图3所示薄壁构件,该构件为关于x与y的双对称截面,故形心O与弯曲中心重合。设弯曲中心即原点O在x方向的位移为u,弯曲中心即原点O在y方向的位移为v。因为y方向的刚度为无穷大,故v=0。
由图3及图4可知:钢梁下翼缘横截面纵向压力为:
P=σ1tfbf (39)
Mx=σ1I/yc=PI/(tfbfyc) (40)
式中:yc为组合梁全截面钢材重心为坐标;I为组合梁全截面钢材绕其重心的惯性矩;λ=l/n;n为整数。
参考文献[19-20]可得薄壁杆件的中性平衡微分方程为:
 (41)
(41)
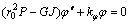 (42)
(42)
式中: 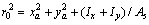 ;As为钢梁截面积;xa为下翼缘截面弯曲中心横坐标;xa=0;ya为下翼缘截面弯曲中心纵坐标,ya=0;
;As为钢梁截面积;xa为下翼缘截面弯曲中心横坐标;xa=0;ya为下翼缘截面弯曲中心纵坐标,ya=0;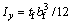 ;
; ;E为钢材拉伸弹性模量;G为钢材剪切弹性模量;φ为腹板下翼缘转角,上标IV表示4次导数。
;E为钢材拉伸弹性模量;G为钢材剪切弹性模量;φ为腹板下翼缘转角,上标IV表示4次导数。
令u=Asin(nπz/l),利用伽辽金法[22]求解方程(41)可得:
 (43)
(43)
令 ,求解微分方程式(42)可得:
,求解微分方程式(42)可得:
 (44)
(44)
由式(43)和(44)及dσcr/dn=0可分别求得钢梁侧向弯曲失稳临界应力σcr1及弯扭失稳临界应力σcr2。比较两者大小,较小者即为组合梁负弯矩区临界应力,由式(40)可进一步获得相应临界弯矩。综上分析可见:负弯矩区组合梁屈曲模式除了侧向弯曲失稳外,还有侧向弯扭失稳。故文献[16,21]仅考虑1种情况的方法是不可取的,有待进一步改进。
3.2 工程实例分析
3.2.1 工程实例1
仍以前面所描述的工程实例为分析对象,计算其负弯矩区钢梁部分的侧向稳定性,不考虑残余应力的影响。其中J=49384.8 mm4,Iy=9.5×105 mm4。
3.2.2 工程实例2
改变实例1中钢梁部分bf与tf,分别取bf=150 mm,tf=7.6 mm,则有J=21 948.8 mm4,Iy=2 137 500 mm4。其他参数均与实例1的相同。计算其负弯矩区钢梁部分的侧向稳定性,不考虑残余应力的影响。
3.2.3 计算结果及比较
表1所示为实例各方法计算比较结果。由表1可知:(1) 算例1中英国钢结构研究院采用的方法[16]所得计算结果、本文计算结果与ANSYS有限元模拟计算结果的偏差不大,而弹性约束压杆的失稳模型 法[21]所得计算结果则与ANSYS有限元模拟计算结果偏差较大。其原因是弹性约束压杆的失稳模型法中利用条元法求解转动约束刚度k的计算公式时未考虑到相邻条元的约束作用,同时没有考虑腹板对翼缘有转动约束作用;(2) 算例2中弹性约束压杆的失稳模型法[21]所得计算结果、本文计算结果与ANSYS有限元模拟计算结果的偏差不大,而英国钢结构研究院采用的方法[16]所得计算结果则与ANSYS有限元模拟计算结果的偏差较大。其原因是英国钢结构研究院采用的方法考虑了整个截面的圣维南扭转,但未考虑到屈曲波长的影响。
表1 多种计算结果的比较
Table 1 Comparisons of multiple results MN·mm

总之,文献[16]和[21]中2种计算方法所得计算结果均与ANSYS有限元模拟计算结果存在一定偏差,而本文方法则与有限元计算结果较吻合,验证了其正确性。
4 结论
(1) 转动约束刚度kf及侧向约束刚度kx均与下翼缘应力σ1呈线性关系,且σ1前系数为正,即σ1越大,则钢梁下翼缘对腹板的转动约束刚度与侧向约束刚度越大。
(2) 转动约束刚度及侧向约束刚度均有可能为负值。当转动约束刚度或侧向约束刚度为负值时,组合梁负弯矩区钢梁屈曲,钢梁下翼缘会受到腹板的转动或侧向约束。
(3)  是1个不为无穷小的数,即下翼缘对腹板的侧向约束刚度是不可以忽略的。因此,在简化计算过程中,不能取kx=0。在理论上论证了工形钢-混凝土组合梁构件中下翼缘对腹板侧向约束刚度不能近似为0,指出了组合结构理论与钢结构理论不同之处。
是1个不为无穷小的数,即下翼缘对腹板的侧向约束刚度是不可以忽略的。因此,在简化计算过程中,不能取kx=0。在理论上论证了工形钢-混凝土组合梁构件中下翼缘对腹板侧向约束刚度不能近似为0,指出了组合结构理论与钢结构理论不同之处。
(4) 本文方法计算结果与有限元计算结果较吻合,验证了本文方法的正确性。其原因是本文所得的屈曲弯矩计算公式同时考虑了侧向弯曲屈曲及侧向弯扭屈曲2种屈曲模式,物理概念清晰,比现有的仅考虑1种屈曲模式的计算方法更合理。同时,本文方法所得计算公式形式较简洁,适于工程应用。
参考文献:
[1] GB 50017—2003, 钢结构设计规范[S].
GB 50017—2003, Steel structure design code[S].
[2] 聂建国. 钢-混凝土组合梁结构试验、理论与应用[M]. 北京: 科学出版社, 2005: 381-388.
NIE Jian-guo. Steel-concrete composite beam structure- experiment, theory and application[M]. Beijing: Science Press, 2005: 381-388.
[3] 王连广. 钢与混凝土组合结构理论与计算[M]. 北京: 科学出版社, 2005: 401-413.
WANG Lian-guang. Steel and concrete composite structure theory and calculation[M]. Beijing: Science Press, 2005: 401-413.
[4] 刘维亚, 钟善桐, 姜维山, 等. 钢与混凝土结构理论与实践[M]. 北京: 中国建筑工业出版社, 2008: 543-551.
LIU Wei-ya, ZHONG Shan-tong, JIANG Wei-shan, et al. Theory and practice of steel and concrete structure[M]. Beijing: China Architecture & Building Press, 2008: 543-551.
[5] 吴金秋, 童根树. 不同斜卷边檩条的局部屈曲和畸变屈曲[J].钢结构, 2006, 21(5): 69-73.
WU Jin-qiu, TONG Gen-shu. Local and distortional bucklings of different inclined lipped purlins[J]. Steel Construction, 2006, 21(5): 69-73.
[6] 何保康, 蒋路. 高强冷弯薄壁型钢卷边槽形截面轴压柱畸变屈曲试验研究[J]. 建筑结构学报, 2006, 27(3): 10-17.
HE Bao-kang, JIANG Lu. Experimental study on distortional buckling of high strength cold-formed steel lipped channel columns under axial compression[J]. Journal of Building Structures, 2006, 27(3): 10-17.
[7] Schafer B W. Local distortional and Euler buckling of thin-walled columns[J]. Journal of Structural Engineering, 2002, 128(3): 289-299.
[8] 陈绍潘. 卷边槽钢的局部相关屈曲和畸变屈曲[J]. 建筑结构学报, 2002, 23(1): 27-31.
CHEN Shao-pan. Local Interactive bucking and distortional buckling of lipped channels[J]. Journal of Building Structures, 2003, 23(1): 27-31.
[9] 郭彦林, 张婀娜. 卷边翼缘工形截面构件在轴心压力作用下的稳定承载力研究[J]. 工业建筑, 2009, 39(9): 7-14.
GUO Yan-lin, ZHANG E-nuo. Load-carrying capacity of lipped I-section members under axial load[J]. Industrial Construction, 2009, 39(9): 7-14.
[10] 姚谏, 滕镜光. 冷弯薄壁卷边槽钢弹性畸变屈曲分析中的转动约束刚度[J]. 工程力学, 2008, 25(4): 65-69.
YAO Jian, TENG Jin-guang. Web rotational restraint in elastic distortional buckling of cold-formed lipped channel sections[J]. Engineering Mechanics, 2008, 25(4): 65-69.
[11] 王春刚, 张耀春. 冷弯薄壁斜卷边槽钢轴压构件的稳定性分析[J]. 哈尔滨工业大学学报, 2009, 41(12): 14-19.
WANG Chun-gang, ZHANG Yao-chun. Stability behavior of channels with inclined simple edge stiffeners under axial compression[J]. Journal of Harbin Institute of Technology, 2009, 41(12): 14-19.
[12] 童根树, 夏竣. 工字形截面钢连续梁负弯矩区的稳定性[J]. 建筑钢结构进展, 2007, 9(1): 46-50.
TONG Gen-shu, XIA Jun. Buckling of I-sectional steel beams loaded by negative moments[J]. Progress in Steel Building Structures, 2007, 9(1): 46-50.
[13] 蒋丽忠, 李兴. 钢-混凝土组合梁侧向稳定承载力[J]. 铁道科学与工程学报, 2006, 3(6): 14-18.
JIANG Li-zhong, LI Xing. Lateral buckling elastic solution of steel-concrete composite beams acted on its ends with an equal constant bending moment[J]. Journal of Railway Science and Engineering, 2006, 3(6): 14-18.
[14] 蒋丽忠, 李兴. 等弯矩作用下钢-混凝土组合梁侧向稳定失稳的弹性解[J]. 工业建筑, 2007, 37(增刊): 490-493.
JIANG Li-zhong, LI Xing. Lateral buckling elastic solution of steel-concrete composite beams acted on its ends with an equal constant bending moment[J]. Industrial Construction, 2007, 37(Suppl): 490-493.
[15] 蒋丽忠, 孙林林. 钢-混凝土组合箱梁的侧向屈曲[J]. 华中科技大学学报: 城市科学版, 2008, 25(3): 5-9.
JIANG Li-zhong, SUN Lin-lin. The lateral buckling of steel-concrete composite box-beams[J]. Journal of Huazhdng University of Science and Technology: Urban Science Edition, 2008, 25(3): 5-9.
[16] Lawson R M, Raekham J W. Design of haunehed composite beams in buildings[M]. Steel Construction Institution, 1989: 112-121.
[17] 陈冀. 钢结构稳定理论与设计[M]. 4版. 北京: 科学出版社, 2008: 511-521.
CHEN Ji. Stability of steel structures theory and design[J]. 4th ed. Beijing: Science Press, 2008: 511-521.
[18] 夏志斌, 潘有昌. 结构稳定理论[M]. 北京: 高等教育出版社, 1987: 160-168.
XIA Zhi-bin, PAN You-chang. Structural stability theory[M]. Beijing: Higher Education Press, 1987: 160-168.
[19] 包世华, 周坚. 薄壁杆件结构力学[M]. 北京: 中国建筑工业出版社, 2006: 137-145.
BAO Shi-hua, ZHOU Jian. Thin-walled rods, structural mechanics[M]. Beijing: China Architecture & Building Press, 2006: 137-145.
[20] 陈伯真, 胡毓仁. 薄壁结构力学[M]. 上海: 上海交通大学出版社, 1998: 179-190.
CHEN Bo-zhen, HU Yu-ren. Thin-walled structure mechanics[M]. Shanghai: Shanghai Jiaotong University Press, 1998: 179-190.
[21] 朱聘儒. 钢-混凝土组合梁设计原理[M]. 北京: 中国建筑工业出版社, 1989: 113-130.
ZHU Pin-ru. Steel-concrete composite beam design theory [M]. Beijing: China Architecture & Building Press, 1989: 113-130.
(编辑 陈灿华)
收稿日期:2011-06-16;修回日期:2011-08-24
基金项目:国家自然科学基金面上项目(资51078355);国家自然科学基金重点资助项目(50938008);国家“十二五”科技支撑计划项目(2011BAJ09B02)
通信作者:蒋丽忠(1971-),男,湖南衡山人,教授,从事组合结构抗震方面的研究;电话:0731-82655536;E-mail:lzhjiang@csu.edu.cn