Numerical analysis of 3D spot continual induction hardening on curved surface of AISI 1045 steel
来源期刊:中南大学学报(英文版)2016年第5期
论文作者:汪舟 高恺 秦训鹏 朱生霄
文章页码:1152 - 1162
Key words:spot continual induction hardening; curved surface; heating delay phenomenon
Abstract: In order to investigate and predict the material properties of curved surface AISI 1045 steel component during spot continual induction hardening (SCIH), a 3D model for curved surface workpieces which coupled electromagnetic, temperature and phase transformation fields was built by finite element software ANSYS. A small size inductor and magnetizer were used in this model, which can move along the top surface of workpiece flexibly. The effect of inductor moving velocity and workpiece radius on temperature field was analyzed and the heating delay phenomenon was found through comparing the simulated results. The temperature field results indicate that the heating delay phenomenon is more obvious under high inductor moving velocity condition. This trend becomes more obvious if the workpiece radius becomes larger. The predictions of microstructure and micro-hardness distribution were also carried out via this model. The predicted results show that the inductor moving velocity is the dominated factor for the distribution of 100% martensite region and phase transformation region. The influencing factor of workpiece radius on 100% martensite region and phase transformation region distribution is obvious under relatively high inductor moving velocity but inconspicuous under relatively low inductor moving velocity.
J. Cent. South Univ. (2016) 23: 1152-1162
DOI: 10.1007/s11771-016-0365-8
GAO Kai(高恺), WANG Zhou(汪舟), QIN Xun-peng(秦训鹏), ZHU Sheng-xiao(朱生霄)
Hubei Key Laboratory of Advanced Technology for Automotive Components
(Wuhan University of Technology), Wuhan 430070, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: In order to investigate and predict the material properties of curved surface AISI 1045 steel component during spot continual induction hardening (SCIH), a 3D model for curved surface workpieces which coupled electromagnetic, temperature and phase transformation fields was built by finite element software ANSYS. A small size inductor and magnetizer were used in this model, which can move along the top surface of workpiece flexibly. The effect of inductor moving velocity and workpiece radius on temperature field was analyzed and the heating delay phenomenon was found through comparing the simulated results. The temperature field results indicate that the heating delay phenomenon is more obvious under high inductor moving velocity condition. This trend becomes more obvious if the workpiece radius becomes larger. The predictions of microstructure and micro-hardness distribution were also carried out via this model. The predicted results show that the inductor moving velocity is the dominated factor for the distribution of 100% martensite region and phase transformation region. The influencing factor of workpiece radius on 100% martensite region and phase transformation region distribution is obvious under relatively high inductor moving velocity but inconspicuous under relatively low inductor moving velocity.
Key words: spot continual induction hardening; curved surface; heating delay phenomenon
1 Introduction
The induction hardening is the most popular application of induction heat treatment, which has three most common forms including surface hardening, through hardening and selective hardening [1]. The aim of surface induction hardening is to provide a martensite layer on workpiece surface to increase the hardness, strength as well as wear resistance, while allowing the remainder of the part to be unaffected by the process. Meanwhile, the aim of selective hardening is to localize a particular area to be hardened. The spot induction hardening (SIH) method, which combines the advantages of surface induction hardening and selective hardening, has been presented by GAO et al [2]. The inductor of SIH method is usually a single-turn copper coil with a small size, which can heat up a very small region of metal workpiece. However, the main disadvantage of SIH method is the lack of flexibility. As the inductor of SIH method cannot move, the requirement cannot be realized if many small or relatively large region of workpiece surface layer needs to be hardened. In order to increase the flexibility of SIH method, spot continual induction hardening (SCIH) method, which is a modified SIH method, is present in the previous work of CHEN [3] and GAO [4]. Compared with SIH method, the inductor (a single-turn copper coil), which carries harmonic current with high frequency, can move along the workpiece surface with a low velocity. In SCIH process, the workpiece surface layer is gradually heated above the complete austenitizing temperature (AC3) by the moving inductor and then cooled by spraying water. As the austenite structure transforms to the martensite structure, the surface layer of workpiece becomes much harder. In order to heighten heating efficiency of the inductor, a magnetizer is installed on the inductor in SCIH process. As the dimension of single-turn copper coil and the magnetizer is usually relatively small compared with the geometry size of the whole workpiece, the moving inductor can realize the heat treatment on many small and relatively large region of curved or some other complicated shape surface. Figure 1 shows the schematic diagram of SCIH process for the curved surface workpiece.
Compared with modeling of spot induction
hardening (SIH), modeling of SCIH is more difficult because this work not only needs to couple temperature and electro-magnetic field as well as phase transformation during SCIH process, but also needs to consider mutual interaction of the non-linear electromagnetic and non-stationary temperature fields under time-dependent boundary conditions. There are relatively numerous works of simulating induction heating or induction hardening process, whose relative position between inductor and workpiece is fixed. However, the works dealing with non-stationary inductor are relatively rare [5-6].
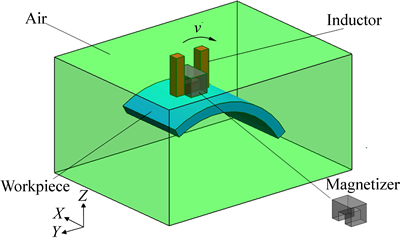
Fig. 1 Schematic diagram of SCIH process for curved surface workpiece
Therefore, in this work, 3D FE model of SCIH process, which coupled electromagnetic and temperature fields and considered phase transformation was built in ANSYS software according to nonlinear equations of electromagnetic and temperature fields. The analysis of temperature evolution with time, micro-structure and micro-hardness distribution was carried out via this model.
2 Mathematical model
2.1 Electro-magnetic field
In the process of induction hardening, the electromagnetic model is based on the set of Maxwell equations [7]:
Magnetic flux equation:
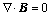 (1)
(1)
Maxwell–Gauss equation:
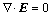 (2)
(2)
Maxwell–Faraday equation:
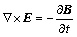 (3)
(3)
Maxwell–Ampere equation:
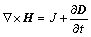 (4)
(4)
where H denotes the magnetic field intensity, B is the magnetic flux density, E is the electric field intensity, D is the electric flux density and J is the electric current density.
The displacement current density 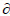 D/
D/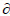 t is negligible compared to the conduction current density while magneto-quasi-static or eddy-current problems are considered [8]. Thus, Eq. (4) can be simplified to Eq. (5) as follows:
t is negligible compared to the conduction current density while magneto-quasi-static or eddy-current problems are considered [8]. Thus, Eq. (4) can be simplified to Eq. (5) as follows:
 (5)
(5)
The above field equations (1), (2), (3) and (5) are supplemented by constitutive relations:
J=σE (6)
B=μH=μ0μrH (7)
where σ is the electric conductivity, μ is the magnetic permeability, μ0 is the permeability of free space and μr is the relative permeability. Both σ and μ are assumed to be isotropic and temperature-dependent. It is difficult to calculate the electric field intensity and magnetic field intensity during the process of electromagnetic field and eddy current field analysis. Therefore, a magnetic vector potential A is introduced, which is defined such that
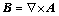 (8)
(8)
Thus, eddy currents field can be described by Eq. (9) through magnetic vector potential A.
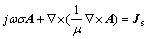 (9)
(9)
where Js is the source current density vector.
2.2 Temperature field
As the process of induction hardening is nonlinear, the temperature field T(x, y, z, t) can be described by the nonlinear 3D transient heat conduction equation as follows [9]:
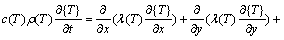
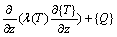 (10)
(10)
 (11)
(11)
where c denotes the specific heat capacity, ρ is mass density, T is temperature vector, 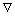 is Laplacian operator, and Q is the volume energy density of heat source.
is Laplacian operator, and Q is the volume energy density of heat source.
The calculation of the temperature distribution in workpiece during the continual induction heating and subsequent quenching requires a solution of the heat equation with convection and radiation boundary conditions during SCIH process. The boundary condition in the model can be expressed as
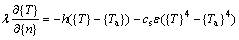 (12)
(12)
where h denotes the convective heat transfer coefficient, Ta is ambient temperature, cs is the emissivity, ε is the Stefane-Boltzmann constant, and {n} is the outward normal of workpiece surface. As the heating period of SIH process lasts only very few seconds and then the heated part is cooled by spraying water, compared with the heat convection, the heat radiation could be neglected [10-11]. The boundary condition in the model can be simplified to
 (13)
(13)
2.3 Phase transformations
The material under investigation, AISI 1045 steel which is normalized at 850 °C, has the nominal chemical composition given in Table 1.
Table 1 Nominal chemical composition of AISI 1045 steel (mass fraction, %)

In order to investigate different types of phase transformations during the SCIH process and micro-structure and micro-hardness after the SCIH process, a continuous cooling transformation (CCT) phase diagram of 1045 steel was carried out in the phase transformation model. The CCT diagram of 1045 steel is depicted in Fig. 2 [12].
It is well known that the austenite transformation is related to many factors such as the heating temperature, heating time, initial micro-structure, carbon content and alloying element. As the workpiece is normalized AISI 1045 steel, whose initial micro-structure, carbon content and alloy element are determined, the heating temperature and the heating time are the only two factors considered for the specific material. In order to simplifythe calculation of austenite transformation amount during heating process in SCIH model, it is assumed that the percentage of austenite transformation is linear while temperature ranges from starting austenitizing temperature (AC1, about 740 °C for AISI 1045) to complete austenitizing temperature (AC3, about 800 °C for AISI 1045). The assumption means that the percentage of austenite transformation is 0% at 740 °C and the percentage of austenite transformation is 100% at 800 °C.
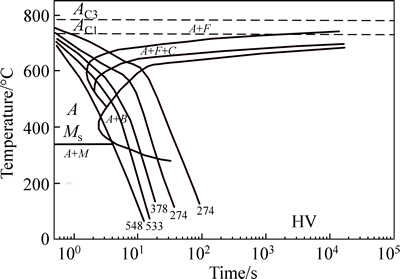
Fig. 2 Continuous cooling transformation curves of AISI 1045 steel
According to the CCT diagram of 1045 steel, it can be seen that different cooling rates lead to different phase transformations and there is a direct relationship between cooling rate and micro-hardness. If austenitizing process is completed, 100% martensite structure can be obtained when the cooling rate is more than 200 K/s; 100% pearlite structure can be obtained when the cooling rate is less than 21 K/s; bainite transformation may appear when the cooling rate is between 21 K/s and 200 K/s [13]. The micro-hardness can be obtained by considering the material chemical composition, the final micro-structure and the cooling rate in this model. The calculation formula for micro-hardness of martensite is given by MAGNABOSCO et al [14]:
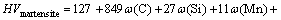
 (14)
(14)
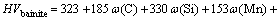
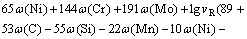
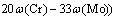 (15)
(15)
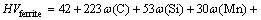

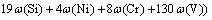 (16)
(16)
where vR is the cooling rate at 700 °C. It can be seen that for 1045 steel, the micro-hardness of micro-structure is only influenced by the cooling rate (vR) while the material chemical composition is certain. According to the assumption of austenite transformation percentage and Eqs. (14)-(16), the calculation formula for micro- hardness value of micro-structure after SCIH process follows:
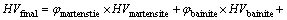
 (17)
(17)
where φ is the volume fraction of micro-structure, and HVoriginal is the hardness of workpiece original structure.
3 Finite element modeling of SCIH
The arrangement of spot continual induction hardening is depicted in Fig. 3. It consists of four domains: inductor (Ω1), magnetizer (Ω2), workpiece (Ω3) and air (Ω4). Symbols A, B and C denote the starting, middle and end positions of the inductor during SCIH process. The inductor carries the high frequency harmonic current which can induce alternating magnetic field to heat curved surface workpiece. In addition, the magnetizer changes the magnetic field distribution around the inductor and heightens both heating efficiency of the inductor and heat treatment quality of the workpiece. The inductor moves along the arc EF with a certain velocity till the computation ends at 7.2 s. During the whole simulated process, the minimum distance between inductor and workpiece is 0.002 m. While the inductor reaches position B at 3.6 s, the cooling water is initially loaded on the workpiece top surface which ranges from point E to point G and moves with the movement of inductor under the same inductor moving velocity.
The geometrical data are shown in Fig. 4. The basic information and the geometrical data are as follows:
1) Inductor material: copper. w1=w2=0.01 m, l1=0.04 m, h1=0.04 m, and h2=0.03 m. Current value I= 1600 A, and frequency f=30 kHz.
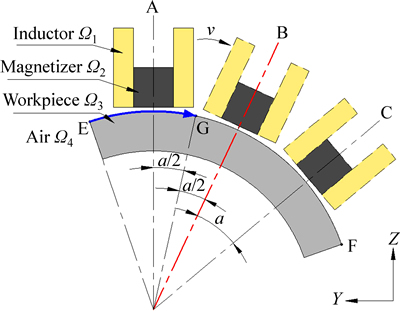
Fig. 3 Basic arrangements of SCIH in different times during treatment
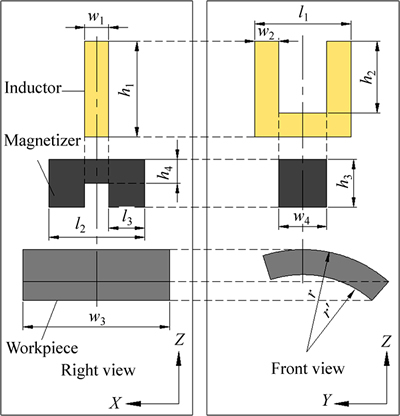
Fig. 4 Geometrical data used in simulation
2) Magnetizer material: ferrite. l2=0.04 m, l3= 0.015 m, h3=0.02 m, h4=0.01 m, and w4=0.02 m.
3) Workpiece material: AISI 1045 steel. w3=0.08 m, and r – r′=0.01 m.
4) Temperature: initial temperature of workpiece Tinitial=20 °C, and temperature of ambient air Ta=20 °C.
5) Heat transfer coefficient of spray water for cooling: αw=10000 W/(m2·K).
The thermal and electro-magnetic properties with change of temperature of AISI 1045 steel are depicted in Fig. 5 [15]. The FE mesh of the whole model and the FE mesh of inductor, magnetizer and workpiece are shown in Fig. 6(a) and Fig. 6(b), respectively. The tetrahedral mesh was generated in the air, inductor and magnetizer region and the hexahedron mesh was generated in the workpiece region. The number of elements of the workpiece, inductor, magnetizer and air were 38640, 4152, 5225 and 422490, respectively. The current entered from A face and out-flowed from B face of inductor. The eddy current concentrated in the surface layer of the workpiece due to the well-known skin-effect, which led to a large temperature gradient in the workpiece surface layer. Therefore, the mesh of surface layer was subdivided in order to obtain reliable results. The minimum distance between nodes was 0.15 mm in this region.
The element type Solid117 was used in electromagnetic field and the element type Solid90 was used in temperature field. Electromagnetic and temperature fields were coupled in ANSYS indirectly, the Joule heat generated in electromagnetic field by eddy current was input as initial load on the temperature field, and then every node temperature in temperature field was stored and reread in the next step, which was taken as the initial condition for the next electromagnetic and temperature analysis. The value of temperature- dependent material properties was updated and the position of inductor changed after △t. The cooling water started loading on workpiece top surface at 3.6 s during SCIH process. The flow chart of coupled electro- magneto-thermal analysis is shown in Fig. 7. The simulation environment was the ANSYS Multi-physics. The computation was performed on an Intel Xeon Dual core processor E5645 2.40 GHz personal computer workstation and the typical CPU time was 33-34 h for each case.
4 Simulation results
4.1 Temperature field results
In order to study the effect of inductor moving velocity and workpiece radius on temperature field during the SCIH process, three different inductor velocities (linear velocity) and workpiece radii (outside radius) are chosen in this model. The parameters for each simulation are given in Table 2.
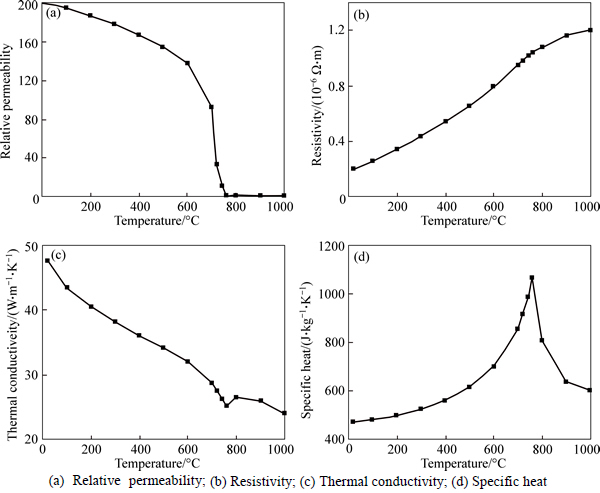
Fig. 5 Thermal and electro-magnetic properties with change of temperature of AISI 1045 steel:
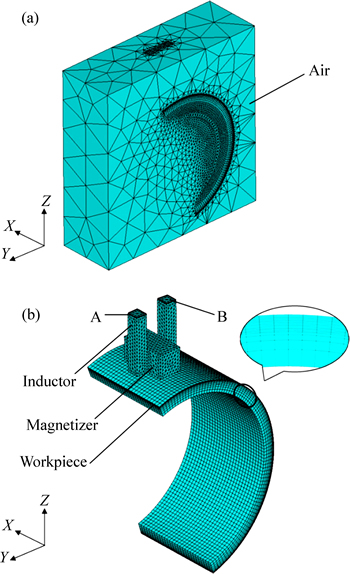
Fig. 6 FE mesh of model
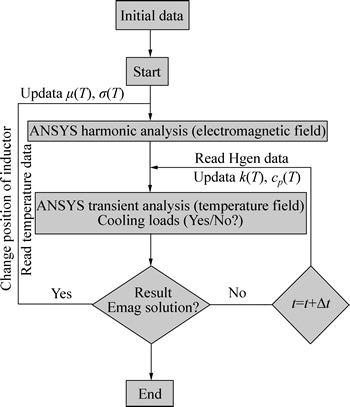
Fig. 7 Flow chart of coupling analysis
Figure 8 shows the highest temperature variation of the whole workpiece (always appearing on treated surface) with time under different inductor moving velocities and workpiece radii conditions. It can be seen that the highest temperature increases very quickly and reaches its stable state in all cases. The time reaching the highest temperature of its stable state becomes shorter with the increment of inductor moving velocity and the highest temperature of its stable state becomes lower with the increment of inductor moving velocity. Meanwhile, the highest temperature of its stable state increases with the increment of workpiece radius if the inductor moving velocities are the same. It can also be seen from Fig. 8 that the highest temperature of its stable state (under v3=0.03 m/s) does not reach AC1 during the whole induction hardening process, which means that austenite transformation does not appear when inductor moving velocity is 0.03 m/s. Therefore, the simulated results (under v=0.03 m/s) are not analyzed in the following work.
Table 2 Operating parameters for simulation

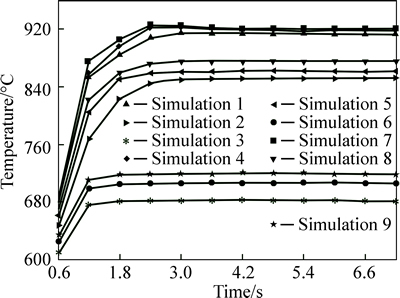
Fig. 8 Highest temperature variations with time of whole workpiece during SCIH process
In order to investigate the heating and cooling process during SCIH process, different observation points on the top surface of a ring-shaped workpiece are chosen. Figure 9 shows schematic diagram of the relative position between observation points and the relative position between the inductor and the workpiece. In Fig. 9, S1 represents the inductor, S2 represents the magnetizer and S3 represents the workpiece. Point Y is the center point of inductor bottom surface. In order to keep the arc distance between observation point the same under different workpiece radii conditions, different central angles (or different radii) between observation points are chosen according to the different workpiece radii. X1-X5 represent the observation points on the workpiece top surface under different workpiece radius and different inductor moving velocities conditions, and all these points are in the center cross-section of workpiece. The projection of Point Y on workpiece top surface (Yp) varies with time and coincides with X1 at t= 3.6 s.
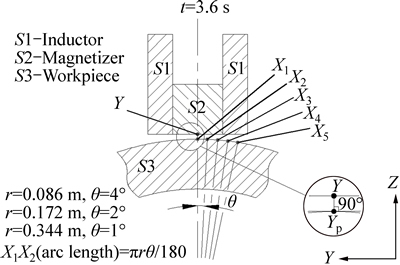
Fig. 9 Schematic diagram of relative position between observation points and relative position between inductor and workpiece
Figure 10 shows the temperature variation with time of the observation points on the workpiece top surface under different workpiece radii and different inductor moving velocities conditions. It can be seen from Fig. 10(a) that the profile of temperature-time curves and the highest temperature of different observation points are nearly the same, and only the times reaching a certain temperature are different. For instance, the temperature of point A1, which is under the condition of r=0.086 m and v=0.01 m/s, increases rapidly when the inductor approaches to this point. As the temperature of Point A1 reaches the Curie temperature (about 760 °C at t=2.7 s), the relative permeability decreases to 0 (see Fig. 5(a)). The relative permeability of the area where is on the left side of Point A1 has already decreased to 1 due to the higher temperature while that of the area where is on the right side of Point A1 is much larger than 1 due to the lower temperature. Therefore, the heating rate of Point A1 decreases inconspicuously from 2.7 s to 3.1 s. At t=3.1 s, the relative permeability of the area on both sides of Point A1 decreases to 0 with the inductor approaching, the heating rate of Point A1 decreases drastically and a knee point appears. However, the highest temperature of Point A1 does not appear at the time when the inductor is right above this point at t=3.6 s. The maximum heat efficiency at t=3.6 s does not mean that the highest temperature appears at this time. The highest temperature of Point A1 (916 °C) appears after the inductor moves away from Point A1 at t=3.8 s (the heating delay phenomenon). At t=3.8 s, the arc distance between Point A1 and the projection of Point Y on workpiece top surface is 0.002 m. After t=3.8 s, the temperature of Point A1 decreases. In this simulation, in order to realize the continual loading of cooling water, workpiece top surface region is divided into a series of continual areas. The cooling water is loaded on these areas with the aim of obtaining martensite transformation. It can be seen from the Fig. 10(a) that the cooling rate becomes higher when the cooling water is loaded on Point A1 at t=5.4 s and t=6 s.
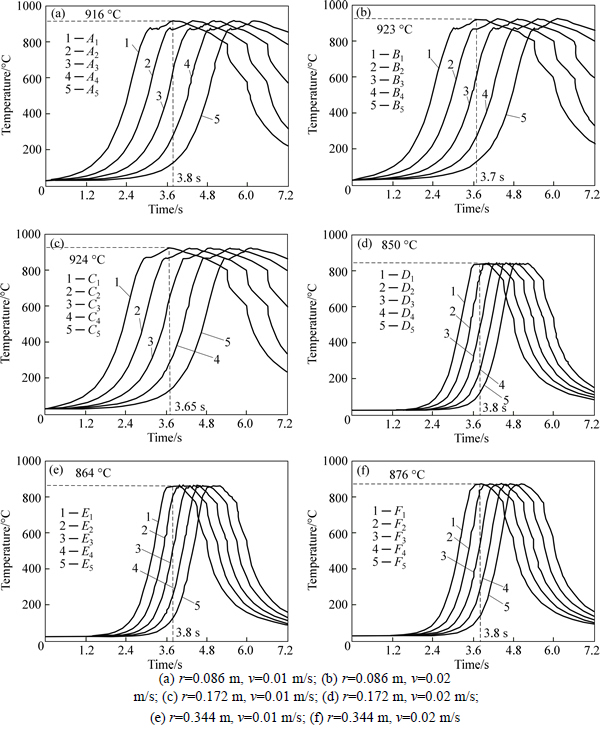
Fig. 10 Temperature-time curves of observation points on workpiece top surface:
Compared with Figs. 10(a), (b) and (c), whose inductor moving velocities are same, it can be seen that the highest temperature values of points A1, B1 and C1 are about 916 °C, 923 °C and 924 °C, respectively, which means that increasing the workpiece radius has little influence on the highest temperature in SCIH process. The appearance times of highest temperature of points A1, B1 and C1 are about 3.8 s, 3.7 s and 3.65 s, respectively, which have already marked in Figs. 10(a), (b) and (c) with dotted line. This phenomenon represents the appearance times of highest temperature of the points on the workpiece top surface (points A1, B1 and C1) decrease with increment of workpiece radius. As mentioned early, when the points A1, B1 and C1 reach their own highest temperatures, the inductor center point (Point Y) has already passed through these points, and the arc distances between points A1, B1 and C1 and the projection of Point Y on workpiece top surface are 0.002 m, 0.001 m and 0.0005 m, respectively. These arc distances become shorter with the increment of workpiece radius. In this simulation, the smaller workpiece radius means the greater curvature. During SCIH process, the air region between the inductor and workpiece becomes larger if the workpiece radius becomes smaller, which means that the inductor heating efficiency becomes lower if the workpiece radius becomes smaller during the process of inductor continual movement.
Figures 10(d), (e) and (f) show that the highest temperatures of points D1, E1 and F1 are 850 °C, 864 °C and 876 °C, respectively, which all appear at t=3.8 s under the condition of v=0.02 m/s. Compared with the condition of v=0.01 m/s, the heating rates and the cooling rates are obviously higher and the highest temperature values are obviously lower under the condition of v=0.02 m/s. The appearance times of the highest temperature of points D1, E1 and F1 have no change with workpiece radius variation, which is different from the condition of v=0.01 m/s. As the heating efficiency of inductor becomes lower when the inductor moving velocity increases from 0.01 m/s to 0.02 m/s, the air region factor has a weak effect on the heating efficiency, which leads to no obvious difference of appearance times of highest temperature of the observation points with different workpiece radii.
In order to investigate the effect of inductor moving velocity on the relative position (relative arc distance) between the observation points (X1-X5) and projection of Point Y on workpiece top surface (Point Yp) when the observation point reaches its own highest temperature, the temperature data in Fig. 10(a) and in Fig. 10(d) are compared and analyzed. It can be seen that under the same workpiece radius (r=0.086 m), the relative arc distances between points A1 and Yp, points D1 and Yp are 0.002 m and 0.004 m, respectively, under the different inductor moving velocities (v=0.01 m/s in Fig. 10(a) and v=0.02 m/s in Fig. 10(d)). According to the same calculation method, as workpiece radius is 0.172 m (Figs. 10(b) and (e)), the relative arc distances between points B1 and Yp, points E1 and Yp are 0.001 m and 0.004 m, respectively. As workpiece radius is 0.334 m (Figs. 10(c) and (f)), the relative arc distances between points C1 and Yp, points F1 and Yp are 0.0005 m and 0.004 m, respectively. It can be concluded that no matter how large the workpiece radius is, the relative arc distance between observation points and Point Yp increases while inductor moving velocity increases from 0.01 m/s to 0.02 m/s, which represents that the heating delay phenomenon is more obvious under high inductor moving velocity condition. This trend becomes more obvious if the workpiece radius becomes larger.
4.2 Prediction of phase transformation region after SCIH process
In this SCIH model, starting austenitizing temperature (AC1), complete austenitizing temperature (AC3) and the cooling rate at 700 °C are three factors for the phase transformation. According to simulated temperature results, the cooling rates at 700 °C of the points whose highest temperatures are larger than AC1 are all larger than 200 K/s. This indicates that only martensite transformation appears during cooling process while bainite and pearlite transformations do not appear in this simulation. Figures 11 and 12 show the schematic diagram of workpiece cross-section and the micro- structure distribution in this cross-section respectively. The red region represents 100% martensite region, the green region represents transitional region and the blue region represents pearlite region in Fig. 12. Compared with Figs. 12(a), (b) and (c), whose inductor moving velocities are all 0.01 m/s, it can be seen that the maximum widths of 100% martensite region and phase transformation region are all 5.6 mm and 8.4 mm, respectively. The maximum widths of these two kinds of regions have no difference under different workpiece radius conditions due to the following two reasons. On one hand, the mesh is divided coarsely in the X-direction, and on the other hand, the perpendicular distance between inductor and workpiece is always 0.002 m in XZ cross-section (in Fig. 11), which is not affected by the variation of workpiece radius. The maximum depths of 100% martensite region in Figs. 12(a), (b) and (c) are all 1.35 mm. The maximum depths of phase transformation region are 1.8 mm, 1.95 mm, and 1.95 mm, respectively. From these data, it can be concluded that increasing workpiece radius has little influence on the distribution of 100% martensite region and phase transformation region under relatively low inductor moving velocity. From Figs. 12(d), (e) and (f), whose inductor moving velocities are 0.02 m/s, it can be seen that the maximum widths of 100% martensite region and phase transformation region are all 4.2 mm and 7 mm under different workpiece radius conditions. The maximum depths of 100% martensite region in Figs. 12(d), (e) and (f) are 0.45 mm, 0.6 mm and 0.75 mm, respectively. The maximum depths of phase transformation region are 0.9 mm, 1.05 mm and 1.2 mm. From these data, it can be concluded that increasing workpiece radius has a great influence on the distribution of 100% martensite region and phase transformation region under relatively high inductor moving velocity. By comparing Figs. 12(a) and (d), it is obvious to see that relatively low inductor moving velocity can make the 100% martensite region and phase transformation region larger, which is due to more heating time in unit area during SCIH process. In summary, the inductor moving velocity is the dominated factor for the distribution of 100% martensite region and phase transformation region. The influencing factor of workpiece radius on 100% martensite region and phase transformation region distribution is obvious under relatively high inductor moving velocity but inconspicuous under relatively low inductor moving velocity.

Fig. 11 Schematic diagram of workpiece cross-section and relative position between inductor and workpiece
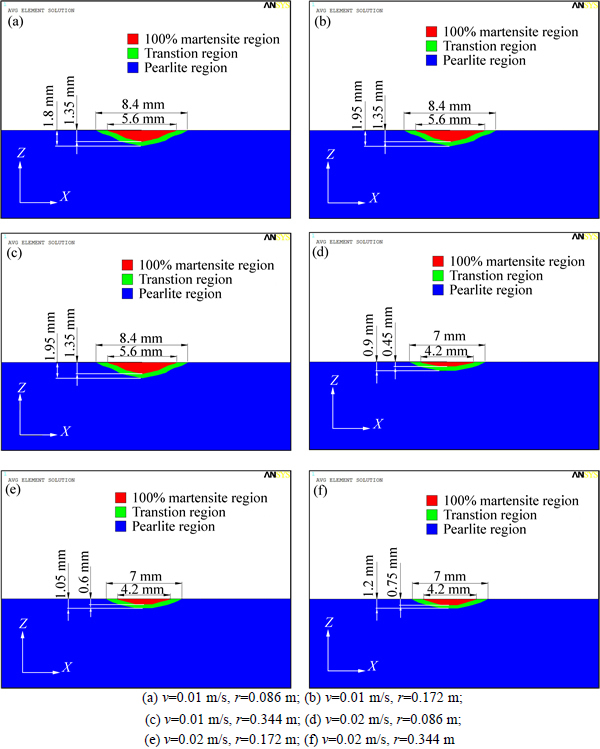
Fig. 12 Micro structure distribution in transverse cross-section of workpiece:
Figure 13 shows the evolution of martensite and pearlite content in depth direction of the workpiece under different inductor moving velocities and workpiece radium conditions. It can be seen that the content of martensite decreases with the increment of depth while that of pearlite increases with the increment of depth in the transitional region. Compared with Figs. 13(a), (b) and (c), it can be seen that the depth of 100% martensite region keeps constant in different workpiece radius conditions. However, the depth of transitional region increases with the increment of workpiece radius. In the transitional region, the content of martensite in the same depth increases with the increment of workpiece radius. This phenomenon also appears in Figs. 13(d), (e) and (f), where the inductor moving velocity is 0.02 m/s.
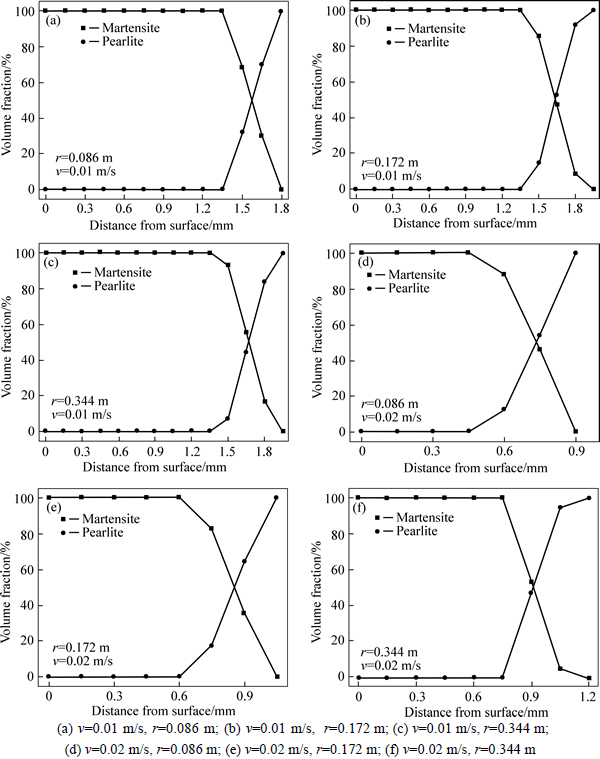
Fig. 13 Evolution of martensite and pearlite contents in depth direction of workpiece:
Figure 14 shows the hardness distributions in depth direction under different inductor moving velocities and workpiece radii, which are calculated according to Eqs. (19). Similar to the microstructure profile, the depth of hardened region is obviously greater under the condition of v=0.01 m/s. By comparing Figs. 14(a) with (b), it can be seen that the maximum hardness value under the condition of v=0.02 m/s is larger than that of v=0.01 m/s. By comparing Figs. 13 with 14, it can be seen that the maximum hardness value appears in 100% martensite region. The final hardness value is only related to the cooling rate when volume fraction of martensite is 100% according to Eqs. (14)-(17). Meanwhile, temperature field results in Section 4.1 show that the cooling rate under the condition of v=0.02 m/s is larger than that of v=0.01 m/s, which leads to this phenomenon. In this simulation, the content of martensite depends on the content of austenite because all austenite transforms to martensite via spraying water quenching. However, The criterion of the amount of austenitizing transformation is only related to heating temperature in this model, but actually the complete austenitizing needs a period of time. This unrealistic assumption may lead to the simulation error of the content of martensite. Furthermore, no consideration of grain size may be another reason for simulation error of microhardness distribution. These two flaws need to be improved in the next work.
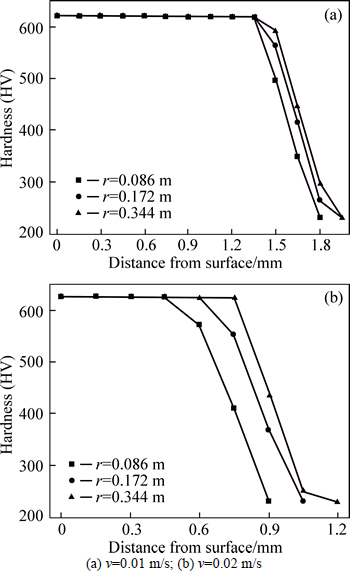
Fig. 14 Hardness distribution in depth direction of workpiece:
5 Conclusions
1) No matter how large the workpiece radius is, the relative position (relative arc distance) between the observation points (X1-X5) and projection of Point Y on workpiece top surface (point Yp) when the observation point reaches the highest temperature increases with inductor moving velocity increasing from 0.01 m/s to 0.02 m/s, which represents that the heating delay phenomenon is more obvious under high inductor moving velocity condition. This trend becomes more obvious if the workpiece radius becomes larger.
2) In SCIH process, the inductor moving velocity is the dominated factor for the distribution of 100% martensite region and phase transformation region. The influencing factor of workpiece radius on 100% martensite region and phase transformation region distribution is obvious under relatively high inductormoving velocity but inconspicuous under relatively low inductor moving velocity.
3) The maximum hardness value under the condition of v=0.02 m/s is larger than that of v=0.01 m/s. Ignoring austenitizing time and the grain size may be the two unrealistic assumptions for the simulation of microstructure and microhardness distribution, which should be improved in the SCIH model.
References
[1] RUDNEV V, LOVELESS D. Induction hardening: Technology, process design, and computer modeling [J]. Comprehensive Materials Processing, 2014, 12: 489-580.
[2] GAO Kai, QIN Xun-peng, WANG Zhou, CHEN Hao, ZHU Sheng-xiao, LIU Yan-xiong, SONG Yan-li. Numerical and experimental analysis of 3D spot induction hardening of AISI 1045 steel [J]. Journal of Materials Processing Technology, 2014, 214(11): 2425-2433.
[3] CHEN Hao. Finite element analysis of 3D spot induction hardening [D]. Wuhan University of Technology, China, 2013. (in Chinese)
[4] GAO Kai. Numerical analysis of spot induction hardening of curved surfacemould [D]. Wuhan, China: Wuhan University of Technology, 2014. (in Chinese)
[5] KRANJC M, ZUPANIC A, MIKLAVCIC D, JARM T. Numerical analysis and thermographic investigation of induction heating [J]. International Journal of Heat and Mass Transfer, 2010, 53(17/18): 3585-3591.
[6]  M C, SALGADO P, V
M C, SALGADO P, V ZQUEZ, R. Numerical simulation of a thermo-electromagneto- hydrodynamic problem in an induction heating furnace [J]. Applied Numerical Mathematics, 2009, 59(9): 2082-2104.
ZQUEZ, R. Numerical simulation of a thermo-electromagneto- hydrodynamic problem in an induction heating furnace [J]. Applied Numerical Mathematics, 2009, 59(9): 2082-2104.
[7] NAAR R, BAY F. Numerical optimisation for induction heat treatment processes [J]. Applied Mathematical Modelling, 2013, 37(4): 2074-2085.
[8] di LUOZZO N, FONTANA M, ARCONDO B. Modelling of induction heating of carbon steel tubes: Mathematical analysis, numerical simulation and validation [J]. Journal of Alloys and Compounds, 2012, 536(1): S564-S568.
[9] CHO K. Coupled electro-magneto-thermal model for induction heating process of a moving billet [J]. International Journal of Thermal Sciences, 2012, 60: 195-204.
[10]  I, BARGLIK J, ULRYCH B. Continual induction hardening of axi-symmetric bodies [J]. Journal of Materials Processing Technology, 2005, 161(1/2): 269-275.
I, BARGLIK J, ULRYCH B. Continual induction hardening of axi-symmetric bodies [J]. Journal of Materials Processing Technology, 2005, 161(1/2): 269-275.
[11] KARBAN P,  M. Continual induction hardening of steel bodies [J]. Mathematics and Computers in Simulation, 2010, 80(8): 1771-1782.
M. Continual induction hardening of steel bodies [J]. Mathematics and Computers in Simulation, 2010, 80(8): 1771-1782.
[12] LEE S J, PAVLINA E J, van TYNE C J. Kinetics modeling of austenite decomposition for an end-quenched 1045 steel [J]. Materials Science and Engineering A, 2010, 527(13/14): 3186-3194.
[13] WU Xiu-xun, ZHOU Guang-yu, XUN Yu. The application technology of steel hardenability [M]. Beijing: China Machine Press, 1994: 97-106. (in Chinese)
[14] MAGNABOSCO I, FERRO P, TIZIANI A, BONOLLO F. Induction heat treatment of a ISO C45 steel bar: Experimental and numerical analysis [J]. Computational Materials Science, 2006, 35(2): 98-106.
[15] ZHANG Yue-hong. Research on the numerical simulation of temperature field in induction heating [D]. Wuxi, China: Jiangnan University, 2008. (in Chinese)
(Edited by YANG Bing)
Foundation item: Project(51175392) supported by the National Natural Science Foundation of China; Project(2014BAA012) supported by the Key Project of Hubei Province Science & Technology Pillar Program, China; Projects(2012-IV-067, 2013-VII-020) supported by the Fundamental Research Funds for the Central Universities of China
Received date: 2015-02-09; Accepted date: 2015-06-05
Corresponding author: WANG Zhou, PhD; Tel: +86-15387036220; E-mail: wangzhou@whut.edu.cn

