J. Cent. South Univ. Technol. (2011) 18: 1200-1210

DOI: 10.1007/s11771-011-0823-2

Multi-objective optimization for leaching process using improved two-stage guide PSO algorithm

HU Guang-hao(胡广浩), MAO Zhi-zhong(毛志忠), HE Da-kuo(何大阔)

School of Information Science and Engineering, Northeastern University, Shenyang 110004, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: A mathematical mechanism model was proposed for the description and analysis of the heat-stirring-acid leaching process. The model is proved to be effective by experiment. Afterwards, the leaching problem was formulated as a constrained multi-objective optimization problem based on the mechanism model. A two-stage guide multi-objective particle swarm optimization (TSG-  MOPSO) algorithm was proposed to solve this optimization problem, which can accelerate the convergence and guarantee the diversity of pareto-optimal front set as well. Computational experiment was conducted to compare the solution by the proposed algorithm with SIGMA-MOPSO by solving the model and with the manual solution in practice. The results indicate that the proposed algorithm shows better performance than SIGMA-MOPSO, and can improve the current manual solutions significantly. The improvements of production time and economic benefit compared with manual solutions are 10.5% and 7.3%, respectively.

Key words: leaching process; modeling; multi-objective optimization; two-stage guide; experiment

1 Introduction

Leaching process is one of the central unit operations in the hydrometallurgical processes. The solution of optimal control problems that appear in leaching process has been a fascinating field of study for several decades. Many such real-world optimal control problems involve simultaneous optimization of multiple performance measures that are often non-commensurable and compete with each other. Historically, optimization techniques have dealt with multiple objectives by combining them into one objective function composed of the weighted sum of individual objectives, or by transforming one objective into a single response function while using others as constraints. For example, the usual objective in optimization of leaching process is to maximize either leaching rate or economic benefit in a minimum time. Like many chemical processes, the leaching process is characterized by a conflict between economic benefit and production time. The multi- objective optimization problem is to find an operating mode that achieves the best trade off between the economic benefit and the production time.

An accurate model of leaching process is necessary for the optimization of controlled variables. Although the leaching reaction with acid has been investigated in recent years [1-6], the reactants in these researches are liquid. A kinetic study of a manganiferous ore leaching in acid media by glucose as the reducing agent is reported in Ref.[1]. A general model of the bacterial leaching process of ferrous and ferric ore is formulated in Ref.[2]. Several series of sulfuric acid leaching tests of a manganese carbonate ore are carried out in Ref.[3]. The overall mass balance model, the population-balance model and the segregated-flow model in acid media are reported in Refs.[4-6]. In this work, the acid leaching of cobalt compound ore which takes sulfur dioxide as the reducing agent is studied. A mathematical mechanism model for leaching process is proposed by analyzing the relationship of leaching rate and controlled variables. The main parameters of the model are estimated by experimental analysis and identification. The validity and generalization of the model are proved by experiment with practical data.

The leaching rate is the most important criterion of leaching process dependent on the optimal controls of heating temperature, flux of sulfuric acid and flux of sulfur dioxide. Considering the complex solution space and nonlinear objective functions, the optimal solution is difficult to gain by many traditional optimization methods. However, several intelligent algorithms have been used to enhance the performance of industrial process, including genetic algorithms [7], particle swarm optimization [8], and evolutionary optimization [9]. Particle swarm optimization (PSO) is one of the most widely used multi-point search algorithms using stochastic behavior. PSO is developed by inspiring with social behavior that is observed in nature such as flocks of birds and schools of fish [10-11]. Recently, PSO has been gained more and more attention, due to its powerful search ability in function optimization. PSO is adopted to the multi-objective optimization widely. The main differences from single-objective PSO are the proper introduction of archive to reserve pareto-optimal candidates and the appropriate selection of guide particles for multi-objective optimization [12]. For example, MOSTAGHIM and TEICH [13] proposed a SIGMA method. This method selected the best local guides for each particle, which mainly improved the convergence to the pareto front. But, the method could not gain good convergence rate and uniform diversity simultaneously. COELLO and LECHUGA [14] introduced the global guide selection method based on pareto optimality and hypercube in the objective function space to maintain the diversity of the particles. But its convergence rate was low. To improve the performance of multi-objective PSO optimization algorithm, a two- stage guide multi-objective particle swarm optimization (TSG-MOPSO) algorithm is proposed in this work, which accelerates the convergence and guarantees the diversity of pareto-optimal front set as well.

In this study, according to the inherent mechanism and manufacturing characteristics of leaching process, a mechanism model for leaching process is proposed. Afterwards, the leaching problem is formulated as a multi-objective optimization problem with secure and technological constraints. TSG-MOPSO algorithm is proposed to solve the proposed multi-objective optimization problem to obtain the optimal setting of heating temperature, flux of sulfuric acid and flux of sulfur dioxide for the leaching process. The leaching process optimization system, which includes the mathematical model and the improved algorithm, is applied in an advanced factory. The practical application results are evaluated.

2 Mathematical mechanism model of leaching process

2.1 Brief introduction of leaching process

Leaching is defined as removal of ore by dissolving them from the solid matrix. The reagent is injected into a leaching tank and dissolves ore to separate useful components and impurities. In this work, cobalt compound is produced in the hydrometallurgical factory, and the reagents are sulfuric acid and sulfur dioxide. The field device is shown in Fig.1. The device can monitor the temperature, pH value, flux of sulfur dioxide and flux of sulfuric acid on line, and detect the leaching rate off line. The whole process is a batch process. The ore is stored in the slurry tank and transported to the leaching tank. And then, the ore pulp is stirred and heated, and reacted with the sulfuric acid and sulfur dioxide in the leaching tank. In the reaction, lower-priced ore reacts with sulfuric acid to generate vitriol, and higher-priced ore reacts with sulfur dioxide to generate vitriol.

Fig.1 Field device of heat-stirring-acid leaching process

2.2 Mechanism model of leaching process

Before modeling, some assumptions for the leaching process are proposed as follows.

1) The solution is stirred uniformly in leaching tank;

2) The temperature of solution is uniform in leaching tank;

3) Reaction is not exothermic;

4) The average specific heat of mixtures has nothing to do with the temperature, and does not change along with the composition of reactant;

5) The sulfur dioxide injected into solution is reacted completely;

6) Classifying ore as two parts: one part is higher- priced ore, and the other is lower-priced ore.

The kinetic study of the leaching process is researched. In the leaching process, the reaction rate is supposed to be controlled by the chemical reaction [1-6, 15-16], then

                                      (1)

where N is the amount of the substance of unleached ore at time t,  t is the reaction time, S is the surface area of a ore particle  k is a constant of reaction, C is the concentration of acid, r_k is the radius of ore particle, ρ is the ore density, and M is the average molar mass of ore. Then, there is

                                    (2)

Because the radius of ore particle is not convenient to be detected, the kinetic equation is usually expressed by the relationship between leaching rate y and reaction time t. N₀ is supposed to be the amount of the substance of unleached ore at beginning, then

                             (3)

where r_k0 is the initial radius of ore particle. Substituting Eq.(3) into Eq.(2) results in

                              (4)

According to Arrhenius equation [17], k is defined as

k=Aexp(-E/RT)                                    (5)

where A is the activation coefficient, E is the activation of ore, R is the gas constant, and T is temperature.

Based on the kinetic analysis on the leaching process above and combined with the actual field production, the material balance equation of leaching process is established as follows.

Lower-priced ore:

               (6)

Higher-priced ore:

               (7)

Total leaching rate:

                                   (8)

where y₁ is the leaching rate of lower-priced ore, y₂ is the leaching rate of higher-priced ore, y₃ is the concentration of sulfuric acid, y₄ is the concentration of sulfurous acid, y₅ is the temperature of leaching solution, y is the total leaching rate, f is the ratio of lower-priced ore in reactant, and φ is the ratio of higher-priced ore in reactant.

In the reaction of leaching process, the concentration of sulfuric acid and the concentration of sulfurous acid are changed. The change of the concentration of sulfuric acid is dependent on two factors: one is the consumption of sulfuric acid during the reaction, and the other is the supplement of sulfuric acid during the reaction. Considering these two factors, the material balance of sulfuric acid can be formulated as the following differential equation:

          (9)

where K₁=χ?G/M, C_con is the concentration of concentrated sulfuric acid, u₂ is the flux of concentrated sulfuric acid, ρ_con is the density of concentrated sulfuric acid, M_con is the molar mass of concentrated sulfuric acid, χ is the content of lower-priced ore, G is the weight of ore, α is the consumption of amount of the substance of sulfuric acid when 1 mol lower-priced ore is leached, and V is the cubage of leaching tank.

The change of concentration of sulfurous acid is dependent on four factors: 1) consumption of sulfurous acid during the reaction, 2) flux of sulfur dioxide, 3) solubility of sulfur dioxide, and 4) contact area between sulfur dioxide and leaching solution. The dissolution rate [18] and the contact area between sulfur dioxide and leaching solution [19] can be defined as follows.

Dissolution rate:

                            (10)

Contact area:

                              (11)

where D_g is the diffusivity of sulfur dioxide in the water, C_h is the solubility of sulfur dioxide, δ_g is the thickness of gas-liquid contact area, u₃ is the flux of sulfur dioxide, H is the height of leaching tank, μ is the rising velocity of bubble, and r is the radius of bubble.

Considering these factors, the material balance of sulfurous acid can be formulated as following differential equation:

                         (12)

where K₂=γ?G/M, γ is the content of higher-priced ore, and β is the consumption of amount of the substance of sulfur dioxide when 1 mol higher-priced ore is leached.

The leaching process is a heat-acid-stirring reaction. It is also an energy transfer process in which energy is delivered from the heating pipe in leaching tank to the leaching solution, and it can be expressed by the following equation:

                            (13)

where U is the heat transfer coefficient of leaching tank, B is the heat transfer area of leaching tank, u₁ is the heating temperature, m is the mass of leaching solution, and  is the average specific heat of leaching solution.

In summary, the mechanism model of the leaching process may be expressed by Eqs.(6), (7), (8), (9), (12) and (13).

2.3 Parameters of mechanism model

Considering the multi-tudinousness of the parameters in mechanism model, an accurate setting of the parameters is important to the application of the model. The main parameters of the mechanism model are tested by experimental analysis and identification.

2.3.1 Known parameters in field

V=12 000 L, H=500 cm, M=73.31 g/mol, ρ=    8.9 g/cm³, C_con=0.95, ρ_con=1.84 kg/L, M_con=98 g/mol, α= 1, β=4.19, U=27 509 J/(m²?K?s), B=14.13 m² and r=   0.5 cm are used.

2.3.2 Known parameters in literature

μ=10 cm/s [18], R=8.31 J/(K?mol) [18], D_g=    1.21 cm²/s [19] and δ_g=0.74 cm [19] are used.

2.3.3 Parameters obtained from experiment and identification

1) Parameters obtained from experiment

The solubility of sulfur dioxide is a variable parameter about temperature. The solubility of sulfur dioxide drops along with the ascension of temperature. The function of solubility of sulfur dioxide is expressed by the regression analyzing of the experimental data:

   

                 (14)

Similarly, the average specific heat of leaching solution is 2 298.365 J/(kg?K^-1).

2) Parameters obtained from identification

Parameters A, E₁ and E₂ are identified by PSO optimization algorithm with the field actual data. The chart of identification is shown in Fig.2.

The results of the identification are A=68.36, E₁=  68 891 J/mol and E₂=66 529 J/mol.

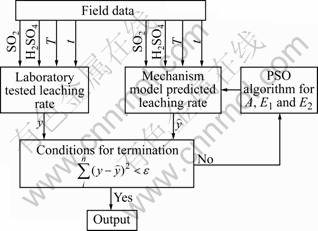
Fig.2 Chart of identification

2.4 Model verification

The predicted leaching rate is compared with the actual leaching rate. The actual leaching rate is collected four times at random, and the comparison between the predicted leaching rate and the actual leaching rate is shown in Fig.3. The relative error (RE) and root mean square error (RMSE) are denoted in Table 1, which are tested by four groups of actual data. The result indicates that the proposed model can predict the leaching rate accurately.

Fig.3 Comparisons between predicted leaching rate and actual leaching rate: (a) Test 1; (b) Test 2; (c) Test 3; (d) Test 4

Table 1 RE and RMSE of four tests

3 Multi-objective optimization model of leaching process

Under the safety conditions, the higher leaching rate, the less consumption and the less production time are significant to the actual production. In the leaching process, the consumption includes three parts: 1) the consumption of steam (temperature), 2) the consumption of sulfuric acid, and 3) the consumption of sulfur dioxide. In this work, two conflict objectives are considered: maximizing the economic benefit and minimizing the production time. A multi-objective optimization model is established which regards the heating temperature u₁, the flux of sulfuric acid u₂, the flux of sulfur dioxide u₃ and production time t_f as the decision variables:

             (15)

where t_f is the production time, Q is the price coefficient of leaching rate, Q₁ is the price coefficient of temperature, Q₂ is the price coefficient of sulfuric acid, Q₃ is the price coefficient of sulfur dioxide, y_min is the expected minimum value of leaching rate, T_max is the maximum value of temperature, T_min is the minimum value of temperature, l_max is the maximum value of flux of sulfuric acid, l_min is the minimum value of flux of sulfuric acid, L_max is the maximum value of flux of sulfur dioxide, L_min is the minimum value of flux of sulfur dioxide, t_max is the maximum value of production time, and t_min is the minimum value of production time. The discrete optimization model can be expressed by the following equation:

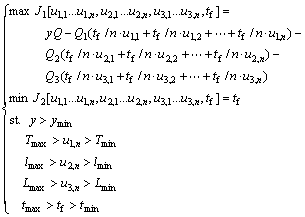(16)

where n is the number of discrete segments of control variables. Solving the multi-objective optimization model, it is important to determine the number of discrete segments of control variables. The more the segments are, the more the difficulties of the optimization and implementation of control strategies are. The less the segments are, the worse the effect of control is. For this reason, the number of discrete segments of control variables needs to be determined by experiment for many times. The result of the experiment indicates that the effect of optimization becomes better and better while the number of discrete segments increases and the improvement stops while the number of discrete segments is more than 8. So, 8 is determined to be the number of discrete segments in this work.

4 Multi-objective PSO algorithm based on two-stage guide

4.1 Basic concepts of multi-objective optimization problems

A general multi-objective optimization (MOP) includes a set of n parameters (decision variables), a set of l objective functions and a set of p inequation constraints and q equation constraints. All objectives are assumed to be minimized in this work, and the problem can be described as

                  (17)

where x is the decision variable, f is the objective function, d is the dimension of decision variable, g_u is the u-th inequation constraint, and h_v is the v-th equation constraint.

Definition 1: Pareto dominance

For any two decision variables, a and b:

The definitions for a maximization problem () are analogical.

Definition 2: Pareto optimality

A decision variable  is said to be non-dominated to set  if and only if

Moreover,  is said to be pareto optimal if and only if  is non-dominated to X.

Definition 3: Non-dominated sets and fronts

Let. The function p(A) gives the set of non-dominated decision variables in A:

The set p(A) is the non-dominated set to A, and the corresponding set of objective functions F(p(A)) is the non-dominated front to A. Furthermore, the set X_p=p(X_F) is called the pareto-optimal set and the set F_P=f(X_P) is denoted as the pareto-optimal front.

4.2 Classical PSO

Particle swarm optimization is a relatively new technique for optimization of continuous non-linear functions [20]. The individuals in a PSO have their own positions and velocities. Each particle moves in the search space with velocity, which is dynamically adjusted and balanced based on its own best movement (p_b) and the best movement of the group (g_b). If the best previous position of the i-th particle is recorded and represented as p_i=( and the global best position is recorded and represented as g_i=   the modification of velocity (v_id) and position (x_id) of the i-th particle can be calculated by the current velocity and the distance from p_i to g_i as shown in the following formulas:

       (18)

x_id=x_id+v_i                                                                     (19)

where w is known as the inertia weight, c₁ and c₂ are two positive constants, r₁ and r₂ are random numbers in the range of [0, 1].

The important part in multi-objective particle swarm optimization (MOPSO) is to determine the global best particle g_i for each particle i of the population. In single objective PSO, the global best particle is determined easily by selecting the particle in the best position. In multi-objective optimization problems, each particle of the population should select its global best particle from the set of pareto-optimal solution.

4.3 Multi-objective PSO algorithm based on two-stage guide (TSG-MOPSO)

Different from normal multi-objective optimization methods that either pay attention to the convergence rate with the cost of worse diversity of solutions or pay attention to the diversity of solutions with the cost of lower convergence rate and more computing time, the TSG-MOPSO method proposed in this work takes both the convergence rate and the diversity of solutions into account. The SIGMA method is adopted to the first half of the evolution because of its fast convergence rate, and an approximated front of pareto is found. And then a proposed ideal optimal particle method is adopted to the remaining half of the evolution that will promote the diversity of solution. This method can both obtain higher convergence rate and ensure better diversity of solutions.

The steps of TSG-MOPSO are shown as follows.

Step 1: Initialize the parameters of TSG-MOPSO, including size of the swarm P, capacity of the archive A, PSO coefficients w, c₁ and c₂, and maximum iterations Z, t=0;

Step 2: Randomly initialize the position and velocity of each particle in set P and set A. Set the initial position as the individual best position p_i of each particle;

Step 3: For t=1 to Z,

1) Update archive,

2) Select the global bests (g_i) from A for each particle in the set P based on the strategy of two-stage guided,

3) Update position and velocity of every particle according to the Eqs.(18)-(19),

4) If t<0.9Z, the particle is mutated according to the proposed strategy,

5) Each particle in set P has a new location, if the current location is dominated by its personal best location (p_i), then the previous location is kept, otherwise, the current location is set as the personal best location. If the particles are mutually non-dominated, one particle is selected randomly;

End.

4.3.1 Strategy of archiving

In normal multi-objective PSO optimization algorithm, the global solution will be stored in the external archive. If the size of the archive exceeds the maximum size limit, it will be truncated using the diversity consideration by crowding distance   mechanism [21] to maintain the diversity of non- dominated solutions.

The crowding distance of a solution provides the density of solutions around this solution [21]. The crowding distance of a solution is the average distance between its two neighbouring solutions. The boundary solutions which have the lowest and the highest objective function values are given an infinite crowding distance values so that they are always selected. The final crowding distance value of a solution is computed by adding the entire individual crowding distances in each objective function.

After all population members in the pareto-optimal set are assigned a distance metric, each solution can be compared with other solutions in the set. A solution with a smaller crowding distance indicates that it is more crowded than other solutions and the diversity of the solution is smaller. On the contrary, a solution with larger distance indicates that the diversity of solutions is larger. So, a solution with larger crowding distance will be reserved and one with smaller crowding distance will be deleted from the external archive to make solutions diversified.

4.3.2 Strategy of two-stage guided

The selection of g_i is the key of PSO algorithm. For MOP problems, g_i is related to the convergence speed of the algorithm and the diversity of solution. A two-stage guide g_i selection strategy is proposed in this work. SIGMA method is adopted to the first half of the evolution because of its fast convergence rate, and an approximated front of pareto is found. And then, a proposed ideal optimal particle method is adopted to the remaining half of the evolution, which will promote the diversity of solution.

1) SIGMA method

The SIGMA method involves choosing the guide particle based on the similarity of the angular position in objective space. This method was proposed by MOSTAGHIM and TEICH [13] and was proved to have good convergence speed. For two-dimensional objective space, δ is defined as

                                         (20)

The guide particle of particles in set P is the particle that has the closest δ in set A.

2) Ideal optimal particle method

Definition 4:  is regarded as the optimal value of the j-th objective, and the point  is called ideal point. The optimal particle x_I of the following equation is the ideal optimal particle:

                     (21)

For a complex multi-objective optimization problem, the optimal value of the each objective and the corresponding optimal point tends to be unknown in advance. In this work, the previous optimal value of each objective in iterative process is regarded as .

The process in which the guide particles are selected from set A is described as the following steps:

(1) Compute the optimal value  and the corresponding optimal particle x^* in set A;

(2) According to Eq.(21), obtain the ideal optimal particle x_I;

(3) Compute the average of the optimal particle x^* and the ideal optimal particle x_I, and regard the average value as g_i.

The value g_i represents the optimal information of the each objective, achieves the global optimization of the algorithm, and is helpful to achieve the local depth search.

3) Selecting guided particle strategy

SIGMA method which has faster convergence rate is adopted to the first n₁-th generation of the evolution, and the ideal optimal particle method is adopted to the remaining (Z-n₁)-th generation.

4.3.3 Strategy of mutation

The use of mutation operator in this MOPSO is needed because the algorithm may converge to local optimal fronts. Mutation probability (P_m) is reduced with the iteration of the algorithm according to

                                 (22)

where C_g is the number of current generation. For each particle, the variable m_r is a random number in the range of [0, 1].

If m_rg, the particle is randomly selected for mutation according to

                        (23)

where μ points out the direction in mutation and θ controls the distance covered by a jump. In this work, μ=3 and θ is set as ±1 randomly. If the solution is beyond its boundary by mutation, it is moved to the corresponding boundary.

5 Practical application and discussion

5.1 Leaching process optimization system

The leaching process optimization system, which is based on the study of the proposed models and the improved algorithm, is developed and put into operation in an advanced factory. In the optimization system, the heating temperature, flux of sulfuric acid and flux of sulfur dioxide are monitored, and a pareto-optimal set of these controlled variables is calculated by the optimization system to the operators, which provides a management guide to the production. The optimization system is developed by C++ and runs on an Intel P4 2.0GHZ PC with 1G RAM. The interface of the leaching process optimization system is shown in Fig.4.

Fig.4 Interface of leaching process optimization system

5.2 Experiment and analysis

Computational experiments are conducted with practical data in order to examine the performance of the proposed TSG-MOPSO and the models. Eighty-two instances are collected from the advanced factory. All the parameters used in the study are listed in Table 2. The proposed algorithm is compared with the SIGMA- MOPSO method. Figure 5 shows the graphical results produced by the TSG-MOPSO and the SIGMA-MOPSO. It is indicated that all the performance indices of the TSG-MOPSO method are better than those of the SIGMA-MOPSO method. By comparing the pareto-optimal fronts produced by each algorithm in the multi-objective optimization problem, it is clear that the TSG-MOPSO generates more solutions which are closed with pareto-optimal front. Moreover, the TSG-MOPSO method has better diversity.

Table 2 TSG-MOPSO parameters used for optimization

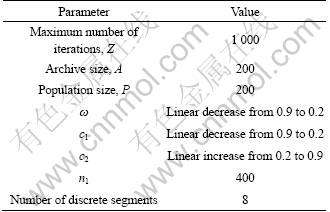
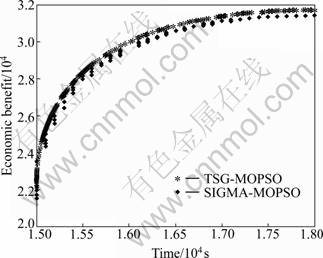
Fig.5 Pareto-optimal front obtained by TSG-MOPSO and SIGMA-MOPSO

Figure 6 shows the evolution process of pareto- optimal front for multi-objective model. The particles iteratively converge on pareto-optimal front.

Fig.6 Evolution of pareto-optimal front for multi-objective model

Figure 7 shows that three representative groups of pareto-optimal solutions. The approximately equal heating temperature denotes that the reaction can be complete under a certain temperature in the leaching process. The sulfuric acid is injected in the first half of reaction because the concentration of sulfuric acid is required by Eq.(6) and Eq.(9) in the beginning of the reaction. The sulfur dioxide is complemented in the whole reaction because the complement of the sulfur dioxide should be equal to the consumption without waste and leak. The complement of sulfuric acid and sulfur dioxide both decrease finally with the reduction of ore. From the foregoing, these pareto-optimal solutions are reasonable and applicable.

Operators choose a optimal solution from the pareto-optimal set obtained by the improved algorithm according to different requirements of production. The optimization system is tested for six months in an advanced factory with practical data in field. Nineteen examples are sampled randomly according to the different masses of every tank of ore. The comparison of these examples between the results of TSG-MOPSO and manual operation is shown in Table 3, and the first three groups of results correspond to three representative groups of pareto-optimal solutions in Fig.7. The mean value of six months is compared in Table 4. It is obvious that the energy consumption is reduced significantly. The production time of the leaching process is reduced by 10.5%, and the economic benefit of factory is increased by 7.3%. The improved algorithm is effective in practice.
 

Fig.7 Three representative groups of pareto-optimal solutions: (a) Pareto-optimal solution 1; (b) Pareto-optimal solution 2;        (c) Pareto-optimal solution 3

Table 3 Comparison of nineteen random examples between optimized and manual operation

Table 4 Comparison of optimization results

6 Conclusions

1) A mathematical mechanism model is proposed by analyzing the heat-stirring-acid leaching process. All the key parameters of the model are obtained from field, literature and identification. The model is verified to be effective with practical data.

2) A multi-objective optimization model is established based on the mathematical mechanism model and the characteristics of the leaching process. Two objectives are considered in the multi-objective model: maximizing the economic benefits and minimizing the production time.

3) A new method named TSG-MOPSO algorithm is proposed to solve this multi-objective optimization problem. The effective archiving strategy, two-stage guide strategy and mutation strategy accelerate the convergence and guarantee the diversity of pareto- optimal front. The proposed algorithm is compared with the SIGMA multi-objective algorithm. The TSG- MOPSO method shows better performance than the SIGMA-MOPSO method.

4) The leaching process optimization system, based on the proposed models and the improved algorithm, is developed and put into operation in an advanced factory. In the optimization system, the production time and economic benefit are improved by 10.5% and 7.3%. The application of the optimization system provides a management guide to the leaching production and reduces the energy consumption significantly.

References

[1] VEGLIO F, TRIFONI M, TORO L. Leaching of manganiferous ores by glucose in a sulfuric acid solution: Kinetic modeling and related statistical analysis [J]. American Chemical Society, 2001, 40(18): 3895-3901.

[2] CRUNDWELL F K. Modeling, simulation, and optimization of bacterial leaching reactors [J]. Biotechnol Bioeng, 2000, 71(4): 255-265.

[3] MA Z, EK C. Rate processes and mathematical modelling of the acid leaching of a manganese carbonate ore [J]. Hydrometallurgy, 1991, 27(2): 125-139.

[4] CRUNDWELL F K. Progress in the mathematical modelling of leaching reactors [J]. Hydrometallurgy, 1995, 39(1/2/3): 321-335.

[5] BREED A W, HANSFORD G S. Modeling continuous bioleach reactors [J]. Biotechnol Bioeng, 1999, 64(6): 671-677.

[6] LEVENSPIEL O. Chemical reactions engineering [M]. New York: John Wiley and Sons, 1972: 33-35.

[7] CHEUNG N, GARCIA A. The use of a heuristic search technique for the optimization of quality of steel billets produced by continuous casting [J]. Engineering Applications of Artificial Intelligence, 2001, 14(2): 229-238.

[8] YANG Zhen-shan, SHAO Cheng, LI Gui-zhi. Multi-objective optimization for EGCS using improved PSO algorithm [C]// Proceedings of the 2007 American Control Conference. New York: American Control Conference, 2007: 5059-5063.

[9] LOTOV A V, KAMENEV G K, BEREZKIN V E. Optimal control of cooling process in continuous casting of steel using a visualization-based multi-criteria approach [J]. Applied Mathmatical Modeling, 2005, 29(7): 653-672.

[10] KENNEDY J, EBERHART R C. Swarm intelligence [M]. Morgan: Kaufmann, 2001: 76-77.

[11] POLI R, KENNEDY J, BLACKWELL T. Particle swarm optimization an overview [J]. Swarm Intelligence, 2007, 1(1): 33-57.

[12] SIERRA M R, COELLO COELLO C A. Multi-objective particle swarm optimizers: A survey of the state-of-the-art [J]. International Journal of Computational Intelligence Research, 2006, 2(3): 287-308.

[13] MOSTAGHIM S, TEICH J. Strategies for finding good local guides in multi-objective particle swarm optimization (MOPSO) [C]// Proceedings of the 2003 IEEE Swarm Intelligence Symposium. Indianapolis: IEEE, 2003: 26-33.

[14] COELLO C A, LECHUGA M S. Handling multiple objectives with particle swarm optimization [J]. IEEE Transactions on Evolutionary Computation, 2006, 8(3): 256-279.

[15] ZHANG Shou-xiang, ZHENG Ya-jie. Study on leaching kinetics of pyrite cinder [J]. Chinese Journal of Chemical Engineering, 2006, 34(11): 36-39. (in Chinese)

[16] TONG Zhi-fang, BI Shi-wen, LI Hui-li, YANG Yi-Hong. Leaching kinetics of calcium aluminate slag [J]. The Chinese Journal of Process Engineering, 2005, 5(4): 399-402. (in Chinese)

[17] LI Hong-gui. Hydrometallurgy [M]. Changsha: Central South University Press, 1998: 42-56. (in Chinese)

[18] PARKER R H. An introduction to chemical metallurgy [M]. Oxford: Pergamon Press Ltd, 1978: 109-112.

[19] MOORE J J. Chemical metallurgy [M]. London: Butterworths Press, 1981: 61-65.

[20] KENNEDY J. The behavior of particles [M]. Heidelberg: Springer Berlin Press, 1998: 213-214.

[21] DEB K, PRATAP A, AGARWAL S, MEYARIVAN T. A fast and elitist multiobjective genetic algorithm: NSGA–II [J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.

(Edited by YANG Bing)

Foundation item: Project(2006AA060201) supported by the National High Technology Research and Development Program of China

Received date: 2010-07-15; Accepted date: 2011-01-18

Corresponding author: HU Guang-hao, PhD; Tel: +86-15998355375; E-mail: guanghao5566@126.com