DOI: 10.11817/j.issn.1672-7207.2018.02.015

2-Club簇图顶点删除问题改进参数算法

谭冠兰¹，孙龙志¹，冯启龙¹，郑莹²，谭培强¹

(1. 中南大学 信息科学与工程学院，湖南 长沙，410083；

2. 长沙理工大学 计算机与通信与工程学院，湖南 长沙，410083)

摘要：2-club簇图修改问题是经典的NP难问题。对通过对2-club簇图修改问题的参数算法进行研究，提出简化问题实例的若干规则。基于对2-club簇图结构的分析和提出的简化规则，并采用自顶向下的分支方法，提出时间复杂度为O^*(3.24^k)的固定参数算法，降低了目前求解该问题的时间复杂度。

关键词：2-club；2-club簇图顶点删除；固定参数算法

中图分类号：TP301             文献标志码：A         文章编号：1672-7207(2018)02-0371-07

Improved algorithm for 2-club cluster vertex deletion

TAN Guanlan¹, SUN Longzhi¹, FENG Qilong¹, ZHENG Ying², TAN Peiqiang¹

(1. School of Information Science and Engineering, Central South University, Changsha 410083, China;

2. School of Computer and Communication Engineering,Changsha University of Science & Technology, Changsha 410083, China)

Abstract: 2-club cluster graph modification problems are classical NP-hard problems. The parameterized algorithms were studied for the 2-club cluster graph modification problems, and several reduction rules were presented to reduce the size of input instance. Based on the structure analysis of the 2-club cluster graph and the reduction rules presented, by applying a top-down approach, a fixed-parameterized algorithm with running time O*(3.24^k) was presented, which improves the current algorithm solving the 2-club cluster graph modification problems.

Key words: 2-club; 2-club cluster vertex deletion; fixed-parameterized algorithm

集群划分^[1]是将数据划分为不同集合的一个过程，使得在同一个集合中的数据是高度相关的。近年来，人们对于数据集群的研究已经提出很多有效方法，如以图为基本模型来研究数据集群^[2-3]。在以图为基本模型的方法研究中，数据被表示为顶点，当且仅当2个数据之间的联系超过规定的阈值时，相应的顶点之间才会有边相连。对稠密子图的数学建模一直是人们研究的热点，最早的研究成果是由LUCE^[4]提出，其方法是用完全子图(complete graph)对稠密子图进行建模。为了避免完全子图模型的不实际性，人们相继提出了很多其他模型，这些模型都是将完全子图模型中的某些条件放松，例如s-club模型、u-clique模型、s-clique模型和s-plex模型^[5]等。基于图模型的数据集群问题可以表示为簇图(cluster graph)修改问题：给定一个无向简单图G，要求通过最少的图修改操作(包括删除顶点、删除边或者删除边和添加边同时操作)将图G转化为另一个图G′，使得图G′中的每个连通分量都是1个稠密子图。其中最著名的簇图修改问题是完全子图修改问题。由于完全子图的松弛模型得到广泛研究，所以，s-club簇图修改问题^[5]、u-clique簇图修改问题^[6]和s-plex簇图修改问题^[7]也得到了人们的广泛关注。假设d_G(u，v)表示图G=(V，E)中任意2个顶点u和v之间的最短距离。图G的直径diam(G)定义为图G中所有顶点之间最短距离的最大值，即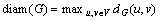。图G的顶点子集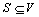是1个s-club当且仅当G[S]的直径不大于s。图G称为s-club簇图当且仅当图G中的每个连通分量为s-club。本文主要研究的是参数化s-club簇图顶点删除问题，具体定义为：

s-club 簇图顶点删除

输入：无向图G=(V，E)，非负整数k。

任务：若存在１个大小不超过k的顶点集合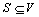，使得G[V\S]的每个连通分量为s-club，则输出集合S，否则输出“NO”。

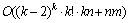给定图是2-club当且仅当任意2个顶点之间或者有边或者有公共邻居。近年来，人们相继提出很多启发式方法来求得最大2-club导出子图^[8-10]。人们也从参数算法2-club导出子图问题进行了研究^[11-13]。SCHFER等^[11]针对如何从图中找到1个至少为k的2-club子图问题，提出了时间复杂度为的参数算法。HARTUNG等^[13-14]分别以反馈顶点集等经典问题作为参数研究2-club子图问题。LIU等^[5]证明2-club 簇图顶点删除问题是NP完全的，提出了时间复杂度为O^*(3.31^k)的固定参数算法。针对2-club 簇图顶点删除问题，本文通过对图结构的分析，利用自顶向下的分支算法提出了时间复杂度为O^*(3.24^k)的固定参数算法。与LIU等^[5]提出的时间复杂度为O^*(3.31^k)的自底向上的参数算法相比，本文提出的分支算法使得分析问题的难度降低，减少了分支情况并且更容易实现。

1  相关术语

假设G=(V，E)是1个无向图，其中V是G的顶点集，E是G的边集，且|V|=n。对于图G，分别用V_G和E_G来表示G的顶点集和边集。设v为图G中的1个顶点，记N(v)为v所有邻居顶点的集合，即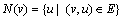，N[v]表示集合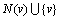。对于顶点子集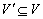，记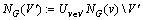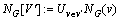，。图G中顶点v的度定义为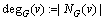。对于顶点子集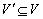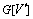，为图G在顶点集合V′上的导出子图。P₄是指含有4个顶点的无弦路径。给定1个P₄ P_stuv，当s和v之间既没有公共邻居也没有边相连时，则P_stuv被定义为严格的P₄。对图G中任何1个顶点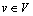，定义v的优先级为图G中包含顶点v的严格P₄的条数，记作δ(v)。

参数计算不仅成为理论计算机科学的一个重要分支，而且在实际中也得到了广泛应用^[16-19]。分支搜索树在参数算法设计中有着广泛应用^{[15, 20]}。若参数为k实例的求解是通过递归求解参数分别为k-d₁，k-d₂…，k-d_i的子实例完成，则称(d₁，d₂，…，d_i)为递归式的分支向量。分支搜索树的大小是通过求解递归式T(k)=T(k-d₁)+T(k-d₂)+…+T(k-d_i)得到的。设α为此递归式的最大解，则称α为分支向量(d₁，…，d_i)的分支数，并用O^*(α^k)表示分支搜索树的大小。

2  简化规则

下面主要介绍2-club 簇图顶点删除算法中用到的一些简化规则。

引理 1  图G的每个连通分量都是1个2-Club当且仅当图G的每个导出子图中都不含有严格P₄。

证明：假设P_stuv为图G中任意1条长度为3的路径，则P_stuv肯定被包含在图G的某个连通分量C中，因为路径P_stuv是连通的。由于图G中的每1个连通分量是1个2-Club，所以，C中任意2点之间或者有边相连或者有公共邻居，则路径P_stuv的边界顶点s和v之间或者有边相连或者有公共邻居。根据严格P₄的定义，路径P_stuv并不是1条严格P₄。因为路径P_stuv是C中长度为3的任意路径，且C是图G的任意1个连通分量，所以，图G中每个连通分量中都不含有严格P₄作为其导出子图，即图G的每个导出子图中都不含有严格P₄。

假设C为图G的任意1个连通分量，且u和v为C中的任意2个顶点。假设u和v之间的最短路径 d_G(u，v)≥3，因为u和v之间是连通的，则u和v之间肯定存在1条长度为3的路径，设为P_staw (s和u以及w和v都有可能为1个顶点，且d_G(s,w)=3。由于d_G(s,w)=3，故s和w之间没有公共顶点。根据严格P₄的定义，P_staw为1条严格P₄，这与图G的导出子图中不含有严格P₄相矛盾，所以，C中任意2个顶点之间的最短距离小于等于2。根据2-Club的定义，C是1个2-Club。又因为C是图G中的任意1个连通分量，故图G的每个连通分量都是1个2-Club。所以，图G是1个2-Club簇图。

根据引理1，只要将图G中所有的严格P₄破坏，则图G中的每个连通分量都是1个2-Club。由于2-Club不具有遗传性质(具有遗传性质的图定义为假设图G具有某种性质Π，若图G的任意导出子图也满足性质Π，则认为图G具有遗传性质)，所以，当删除一条严格P₄中的某个顶点时，原始图有可能会产生新的严格P₄。为了得到时间复杂度更低的固定参数可解算法，将图G中的顶点染为白色顶点和黑色顶点。起初将图G中所有的顶点染为白色顶点，若能确定某个顶点肯定不会被放入解集中，则将该顶点染为黑色。因此，白色顶点意味着不能确定是否放入解集中的顶点，黑色顶点意味着肯定不会被放入解集中的顶点。

定义1  令u 和v是图G中的任意2个顶点。若u和v同时满足以下2个条件，则称v支配u：

1) 删除v不会产生新的严格P₄。

2) 包含u的严格P₄同时也包含v。

引理2  令(G，k)是2-Club簇图顶点删除问题的1个实例，若顶点v和 u都是图G中某条严格P₄的白色顶点并且v支配u，则存在1个最优解不含顶点u。

证明：由于v支配u，故删除v点破坏的严格P₄的数目不会少于删除u点破坏的严格P₄的数目，包含u的解S都可以用v来代替u来形成1个更优的解，所以，顶点u不会在解S中。

基于引理2，可得出以下规则。

规则1  若顶点v和u都是图G某条严格P₄中的白色顶点并且v支配u，则将顶点u染为黑色。

引理3  令(G，k)是2-Club簇图顶点删除问题的1个实例，S是实例(G，k)的1个解。若图G中存在1条严格P₄ f，且f中只剩下1个顶点v没有被染为黑色，则顶点v肯定在解S中。

证明：由于除了顶点v没被染为黑色，f中其他3个点都被染为黑色，这意味着其他3个点都不可能在解S中。为了破坏f，必须将顶点v放在解集S中。

基于引理3，可得出以下规则。

规则2  假设f为图中的一条严格P₄，且f中只剩下1个顶点v没有被染为黑色，则将顶点v放入解集中，并将顶点v从图G中删除，同时将k减1。

引理4  假设e，f为G中的2条严格P₄，且e中的白色顶点集合A是f中白色顶点集合B的子集，则将f标记为已删除。

证明：假设v是集合A中的白色顶点，因为A是B子集，所以，v也是B中的顶点。当删除顶点v时，e会被破坏。同时，f也会被破坏。这表明破坏e的同时会自动破坏f。所以，可以将f标记为已删除。

基于引理4，可得出以下规则。

规则3  假设e，f为图G的2条严格P₄，且e中的白色顶点集合A是f中白色顶点集合B的子集，则将f标记为已删除。

当图G应用这3条规则后，原实例(G，k)中所有的严格P₄ 中的顶点有的已经被染为黑色。所以，在应用分支搜索技术时，可以不考虑这些已经被染为黑色的顶点，而只考虑那些白色的顶点。将严格P₄中白色顶点的个数定义为这条严格P₄的大小。

3  参数算法设计和分析

定义2  令P_stuv为图G中的1条严格P₄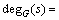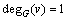， 且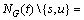 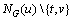，则称P_stuv为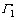结构。

若存在2个顶点w和q分别与t和u相邻且P_wutq也是1条严格P₄，则称P_stuv为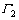结构。

1) 若deg_G(s)和deg_G(v)中至少有1个大于1，假设v点的度大于1，则存在1个顶点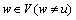与v相邻。若s和w之间有1个公共邻居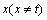，则称P_stuv为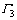结构。

2) 若deg_G(s)和deg_G(v)中至少有1个大于1，假设v点的度大于1，则存在1个顶点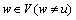与v相邻。若s和w之间没有公共邻居，{t，u}都不和w相邻且t与w之间有1个公共邻居x(x≠u)，则称P_stuv为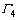结构。

3) 若P_stuv不属于{Γ₁，Γ₂，Γ₃，Γ₄}结构中的任何一种，则称P_stuv为Γ₅结构。

引理5  若图G中不存在{Γ₁，Γ₂，Γ₃，Γ₄}结构，则图G中每条严格P₄中至少存在3个顶点的并且这三个顶点的优先级都至少为2。

证明：设P_stuv为图G中的1条严格P₄。由于图G中不存在{Γ₁，Γ₂，Γ₃，Γ₄}结构，故P_stuv属于Γ₅结构，并且符合以下情况中的一种情况。

情况1：deg_G(s)=deg_G(v)=1且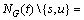 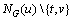。若存在1个顶点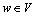与t相邻而不与u相邻，则{t，u，v}被P_stuv和P_wtuv这2条严格P₄包含。

情况2：deg_G(s)和deg_G(v)中至少有1个大于1。假设存在1个顶点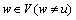与v相邻。

(C1) 若w与s之间没有公共邻居且t与w相邻，则{s，t，v}被P_stuv和P_stwv这2条严格P₄包含。

(C2) 若 w与s之间没有公共邻居，t与w不相邻且u与w相邻，则{s，t，v}被P_stuv和P_stuw这2条严格P₄包含。

(C3) 若{t，u}与w不相邻且{s，t}与w没有公共邻居，则{t，u，v}被P_stwv和P_tuwv这2条严格P₄包含。

在分支时，本文总是优先选择较小严格P₄中的顶点进行分支。在删除Γ₅结构的严格P₄时，算法根据不同的情况选择不同的顶点进行分支，一般选取某个顶点子集中优先级最大的白色顶点进行分支(具体选择哪个顶点进行分支，会在算法的时间复杂度分析过程中体现)，并称此类顶点为关键点。

若当前图G中存在{Γ₁，Γ₂，Γ₃，Γ₄}结构，利用常规的自底向上的分支搜索技术将其破坏，直到图G中不存在{Γ₁，Γ₂，Γ₃，Γ₄}结构为止，则当前图G中剩下的所有严格P₄都不属于{Γ₁，Γ₂，Γ₃，Γ₄}中的某种结构。然后，对图G应用规则1~规则3，则图G中有的严格P₄中的顶点被染为黑色，然后递归的删除Γ₅结构。在删除Γ₅结构时，若图G中产生属于{Γ₁，Γ₂，Γ₃，Γ₄}结构的严格P₄，则首先将其删除。算法的具体过程如图2所示。

图2  2-Club簇图顶点删除问题的固定参数可解算法

Fig. 2  FPT algorithm for 2-club cluster vertex deletion

引理6  令P_stuv为图G中的1条严格P₄。若P_stuv属于{Γ₁，Γ₂，Γ₃，Γ₄}中的任意一种结构，则算法B2CVD可以在O^*(3.24^k)时间内将P_stuv破坏。

证明：根据定义2，可以得到以下4种情况。

情况1：当P_stuv为Γ₁结构时，为了破坏P_stuv，可以分别对{{u}，{v}}进行分支，则分支向量为(1，1)，分支数α≤2。

情况2：当P_stuv为Γ₂结构时，为了破坏P_stuv和P_wtuq，可以分别对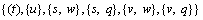进行分支，则分支向量为(1，1，2，2，2，2)，分支数α＜3.24。

情况3：当P_stuv为Γ₃结构时，为了破坏P_stuv和P_sxvw，分别对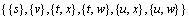进行分支，则分支向量为(1，1，2，2，2，2)，分支数α＜3.24。

情况4：当P_stuv为Γ₄结构时，为了破坏P_stuv和P_stxw，分别对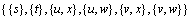进行分支，则分支向量为(1，1，2，2，2，2), 分支数α＜3.24。

综合以上4种情况，算法B2CVD可以在O^*(3.24^k)时间内将P_stuv破坏。

为了分析破坏的图G中所有Γ₅结构的严格P₄的时间复杂度和正确性，本文引入辅助参数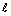。令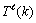代表图G经应用规则1~规则3并且图中没有{Γ₁，Γ₂，Γ₃，Γ₄}结构后，破坏图G中Γ₅结构严格P₄分支搜索树叶子节点的个数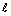，代表图G中至少存在大小不超过3的Γ₅结构严格P₄的条数，k为实例参数。根据文献[15]，含有较少比较严格P₄分支搜索树叶子节点的个数往往比含有较多比较小严格P₄分支搜索树叶子节点个数多，所以，有以下式子成立：

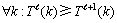            (1)

因此，当考虑到分支搜索树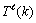的大小时，可以令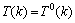。根据公式(4-1)，分析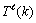大小时，最坏情况是图G中恰好有1条大小不超过3的Γ₅结构的严格P₄，并且这些严格P₄的大小也恰好为3。下面分别通过分析Tⁱ(k)(i=0，1，2)的大小来确定T(k)。除非特别说明，在本文以后的分析过程中，只考虑严格P₄中的白色顶点。

引理7  。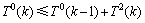

证明：当图G中不存在大小小于4的严格P₄时，根据关键点的定义，算法优先对大小为4的严格P₄中的关键点进行分支。假设x为这些严格P₄的关键点，根据引理5可知，δ(x)≥2。若x在解集S中，则得到1个T⁰(k-1)的分支。若x不在解集S中，则将x着为黑色顶点时至少会产生2条大小为3的严格P₄，至少会得到1个T²(k)的分支，所以， 。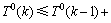

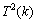2-Club簇图顶点删除问题的固定参数可解算法见图2。

引理8

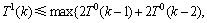
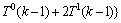
证明：令严格P₄ 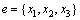是图G中大小为3的1条严格P₄。

情况1：假设f为一条大小为4的严格P₄，使得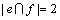 (2条严格P₄相交顶点的个数只考虑它们中白色顶点相交的个数)。根据规则3和引理5可知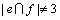， (并且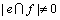)。算法首先会对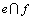中的关键点进行分支。假设x₁是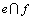中的关键点，则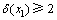。若x₁在解集S中，则得到1个T⁰(k-1)分支。若x₁不在解集S中，算法首先将x₁着为黑色，然后对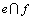中的另一个关键点进行分支，假设另一个关键点为x₂。若x₂在解集S中，则得到1个T⁰(k-1)分支。若x₂不在解集S中，为了破坏e和f，则e中剩下的那个顶点必须放在解集S中，f 中剩下的2个点中至少有1个顶点在解集S中，则得到2个2T⁰(k-2)分支。所以，。

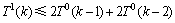情况2：假设f为一条大小为4的严格P₄，使得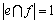。算法首先对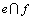中的关键点进行分支。假设x₁是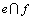中的关键点，则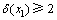。若x₁在解集S中，则得到1个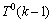分支。若x₁不在解集S中，则将x₁着为黑色，着色后e记为e₁，则e₁的大小为2。同时由于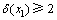，则至少会得到1个大小为3的严格P₄，记为e₂。假设x₂为e₁中e₁的关键点，则算法首先对x₂进行分支。若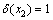，当x₂在解中时，则得到1个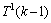分支。当x₂不在解中时，为了破坏e₁，则e₁中剩下的那个顶点必须放入解集S中，同样会得到1个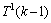分支。若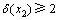，当x₂在解集S中时，由于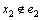，所以，e₂被保留下来，则会得到1个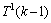分支。当x₂不在解集S中时，则又会产生1条大小为3的严格P₄，记为e₃。为了破坏e₁剩下的那个顶点，假设为x₃，则x₃必须放在解集S中。若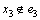，则得到1个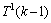分支，否则，则得到1个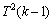分支。根据式(1)，得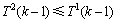，所以，有以下不等式成立：。

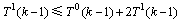引理9

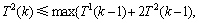
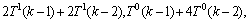
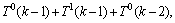
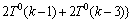
证明：对T²(k)分以下3种情况进行分析。

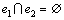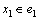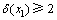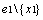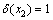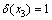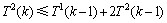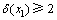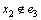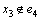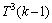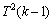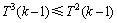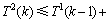
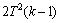情况1：令e₁和e₂是大小为3的2条严格P₄，且。算法首先对e₁和e₂中关键点进行分支。假设关键点为x₁且，根据引理5可知，。若x₁在解集S中，则得到1个T¹(k-1)的分支。若x₁不在解集S中，则至少得到1条大小为3的严格P₄，记为e₃。在下面的递归分支中， 则成为最小的严格P₄。根据关键点的定义，算法继续对e₁中的顶点进行分支。假设x₂为将x₁着为黑色后e₁中的关键点，若，则，x₃为e₁中的另一个点。当x₂在解集S中时，则得到1个T²(k-1)分支。当x₂不在解集S中时，则e₁剩下的那个顶点必须放入解中，则得到1个T²(k-1)分支，因此，。若且，当x₂在解集S时，则得到1个T²(k-1)分支。若x₂不在解集S中时，则至少会得到1个大小为3的严格P₄，记为e₄。因为x₂不在解集S中，故剩下的点x₃必放入解集S中。若，则得到1个分支，否则，则得到1个分支。根据式(1)，，因此， 。若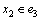，当x₂在解集S中时，则得到1个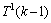分支。当x₂不在解集S中时，为了破坏e₂和e₃，由于e₁中剩下1个顶点和e₃中剩下2个顶点，故可得到1个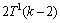分支。因此，根据对T²(k)的具体情况分析，以下式子成立：

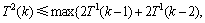
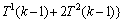
情况2：令e₁和e₂是大小为3的2条严格P₄，且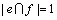。算法首先对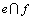中的关键点进行分支。假设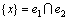。若x在解集S中，则得到1个T⁰(k-1)分支。若x不在解集S中，为了将e₁和e₂破坏，则必须分别在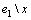和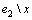中选取1个顶点放入解中。由于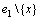和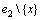中分别剩余2个顶点，最坏情况是剩余所有顶点的优先级为1，所以，共有4种可能T⁰(k-2)分支。根据以上情况分析，有以下式子成立：。

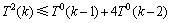情况3：令e₁={x₁，x₂，x₃}和e₂={x₂，x₃，x₄}是大小为3的2条严格P₄，并且e₁和e₂中另一个被着为黑色的点为x₅和x₆，则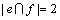。根据引理6可知，若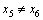，这种结构已经被破坏，所以，x₅=x₆。若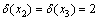，则删除x₅后图G中肯定会引入新的严格P₄，否则，根据规则1，x₁和x₂早已被支配且染为黑色。又因为x₂与x₃之间不能相互支配，所以，删除x₂与x₃都会引入新的严格P₄。因此，删除x₂，x₃和x₅都会引入新的严格P₄。假设x₅是e₁的1个端点(对x₂和x₃顶点类似)，由于图中只存在Γ₅结构，删除x₅所引入新的严格P₄中肯定存在1个顶点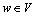，使得w与x₅相邻。根据引理5，除严格P₄e₂外，x₂和x₃中至少存在1个点被2条严格P₄包含。若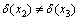，则x₂和x₃中至少有1个点至少被3条严格P₄包含。假设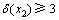，若x₂放入解集中，会产生T⁰(k-1)分支。若x₂不在解集S中，则会产生1条大小为3的严格P₄，记为e₃。若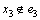，当x₃放入解集S中会产生1个T¹(k-1)分支。若x₃不放入解集S中，为了破坏e₁和e₃，x₁和x₄必须放入解集S中，在最坏情况下会得到1个T⁰(k-2)的分支(当x₁或者x₄在e₃中)。所以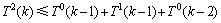，。若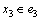，当x₃在解集S中时会得到1个T⁰(k-1)分支。当x₃不在解集S中时，为了支配e₁，e₂和e₃，会得到1个2T⁰(k-3)的分支，则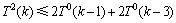。综上所述，可以得到

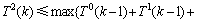
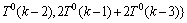
因此，基于对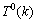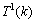，和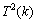的分析，可得到以下不等式方程：

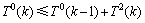
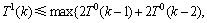
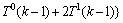
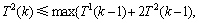
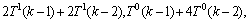
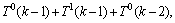
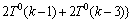
T¹(k)和T²(k)取不同的值，共可以得到10个不等式方程组。下面就其中1个不等式方程组进行求解：

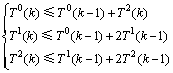        (2)

根据文献[15]，首先将不等式全部看成等式来求解，然后验证其解是否正确。由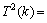 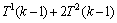，得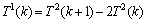，将T¹(k)用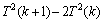代入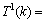 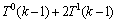，则以下式子成立：。

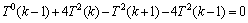将T²(k)用T⁰(k)-T⁰(k-1)代替，则以下式子成立：

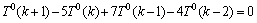
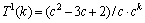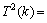
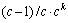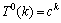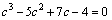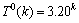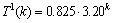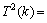
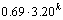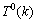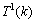令T⁰(k)=c^k，则， 。将代入上式得，，解得c的最大根为3.20，所以，，， 。将，和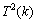的解代入式(2)，式(2)也得到满足。因此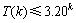，。对其他不等式方程组用同样的方法求解，解得在最坏情况下，。

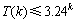引理10  若图G中不存在{Γ₁，Γ₂，Γ₃，Γ₄}结构，则可以在O^*(3.24^k)时间内将图G中Γ₅结构的严格P₄破坏。

定理 给定2-Club簇图顶点删除问题的1个实例(G，S，k)，若存在大小不超过k的解集S，则算法B2CVD(G，S，k)必定在O^*(3. 24^k) 时间内返回解集S，否则返回“NO”。

证明：假设给定2-Club簇图顶点删除问题的1个实例(G，S，k)，为了将图G转化为2-Club 簇图，根据引理1，算法必须破坏图G中所有的严格P₄。算法首先将图G中的严格P₄分为2种：属于{Γ₁，Γ₂，Γ₃，Γ₄}结构的严格P₄和Γ₅结构的严格P₄。针对不同结构的严格P₄，算法采用不同的分支搜索技术将其破坏。算法执行第1步时，若图G中存在{Γ₁，Γ₂，Γ₃，Γ₄}结构的严格P₄，则可以利用引理6的分支方法将其破坏掉并且此步操作是正确的。算法执行完第1步，图G中只存在Γ₅结构的严格P₄，则算法下一步就是将图G中Γ₅结构的严格P₄破坏。算法执行第2步，则对图G应用规则1~规则3，并且根据引理2~引理4，这步操作也是正确的。算法第3步将图G中所有没有被标记为删除的严格P₄放入集合P中。算法执行第4.1步时，若集合P为空且k＞0，则说明算法可以通过删除少于k个顶点将图G中所有的严格P₄删除，因此，可以返回解集S。若集合P不为空且k＞0，则图中仍然存在Γ₅结构的严格P₄，根据启发式规则，找出当前的关键顶点x进行分支。算法第4.4步和4.5步分别对顶点x是否放在解集S中进行分支，递归调用B2CVD(G, S, k)算法，直到求出解集S或者不存在解集为止。由引理10可知对x的分支是正确的。算法第5.1步表示，若k=0且图G中仍然存在严格P₄或者k＜0，则算法不可能通过删除k个点将图G中的所有严格P₄删除，所以返回“NO”。算法第5.2步表示，k=0且图G中没有严格P₄，则算法恰好通过删除k个点将图G中所有严格P₄破坏，因此，图2所示的算法是正确的。

由引理6和引理10可知，删除严格P₄的最坏时间复杂度都为O^*(3.24^k)，因此，整个算法的时间复杂度为O^*(3.24^k)。

4  结论

1) 对2-Club簇图顶点删除问题采用分支搜索技术进行分支，并提出相应的简化规则，得出时间复杂度为O^*(3.24^k)的固定参数可解算法。

2) 2-club簇图修改问题的3个问题仍然没有给出多项式核或证明没有多项式核。这3个问题是否具有多项式核仍有待研究。

参考文献：

[1] XU R, WUNSCH D. Survey of clustering algorithms[J]. IEEE Transactions on Neural Networks, 2005, 16(3): 645-678.

[2] BANSAL N, BLUM A, CHAWLA S. Correlation clustering[J]. Machine Learning, 2004, 56(1): 89-113.

[3] SHAMIR R, SHARAN R, TSUR D. Cluster graph modification problems[J]. Discrete Applied Mathematics, 2004, 144(1): 173-182.

[4] LUCE R D. Connectivity and generalized cliques in sociometric group structure[J]. Psychometrika, 1950, 15(2): 169-190.

[5] LIU H, ZHANG P, ZHU D. On editing graphs into 2-club clusters[C]//Proc Frontiers in Algorithmics and Algorithmic Aspects in Information and Management, FAW-AAIM 2012, LNCS 7285. Beijing, 2012: 235-246.

[6] GUO J, KANJ I A, KOMUSIEWICZ C, et al. Editing graphs into disjoint unions of dense clusters[J]. Algorithmica, 2011, 61(4): 949-970.

[7] GUO J, KOMUSIEWICZ C, NIEDERMEIER R, et al. A more relaxed model for graph-based data clustering:s-plex cluster editing[J]. SIAM Journal on Discrete Mathematics, 2010, 24(4): 1662-1683.

[8] SHAHINPOUR S, BUTENKO S. Algorithms for the maximum k-club problem in graphs[J]. Journal of Combinatorial Optimization, 2012, 26(3): 1-35.

[9] MAHDAVI PAJOUH F, BALASUNDARAM B. On inclusionwise maximal and maximum cardinality k-clubs in graphs[J]. Discrete Optimization, 2012, 9(2): 84-97.

[10] BOURJOLLY J M, LAPORTE G, PESANT G. An exact algorithm for the maximum k-club problem in an undirected graph[J]. European Journal of Operational Research, 2002, 138(1): 21-28.

[11] SCHFER A, KOMUSIEWICZ C, MOSER H, et al. Parameterized computational complexity of finding small-diameter subgraphs[J]. Optimization Letters, 2012, 6(5): 883-891.

[12] HARTUNG S, KOMUSIEWICZ C, NICHTERLEIN A. parameterized algorithmics and computational experiments for finding 2-Clubs[C]//Proceeding 7th International Symposium on Parameterized and Exact Computation, IPEC 2012, LNCS 7535, Ljubljana, Springer, 2012: 231-241.

[13] HARTUNG S, KOMUSIEWICZ C, NICHTERLEIN A. On structural parameterizations for the 2-Club problem[C]// Proceeding 39th International Conference on Current Trends in Theory and Practice of Computer Science. Spindleruv: Springer, 2013: 233-243.

[14] FERNAU H. Parameterized algorithms for hitting set: the weighted case[J]. Theoretical Computer Science, 2010, 411(16): 1698-1713.

[15] CYGAN M. Deterministic parameterized connected vertex cover[C]//Proceeding 13th International Scandinavian Symposium and Workshops on Algorithm Theory. Helsinki: Springer, 2012: 95-106.

[16] COHEN D, CRAMPTON J, GAGARIN A, et al. Iterative plan construction for the workflow satisfiability problem[J]. Journal of Artificial Intelligence Research, 2014, 51(3): 555-577.

[17] GUTIN G, KRATSCH S, WAHLSTRM M. Polynomial kernels and user reductions for the workflow satisfiability problem[C]//Proceeding 9th International Symposium on Parameterized and Exact Computation. Wroclaw: Springer, 208-220.

[18] ABU-KHZAM F N, EGAN J, FELLOWS M R, et al. On the parameterized complexity of dynamic problems[J]. Theoretical Computer Science, 2015, 607(3): 426-434.

[19] JANSEN B M P, KRATSCH S. A structural approach to kernels for ILPs: treewidth and total unimodularity[C]//Proceeding 23rd European Symposium on Algorithm. Patras: Springer, 2015: 779-791.

[20] NIEDERMEIER R. Invitation to fixed-parameter algorithms[M]. Habilitationschrift: University of Tübingen, 2002: 1-30.

(编辑  陈灿华)

收稿日期：2017-02-10；修回日期：2017-04-15

基金项目(Foundation item)：国家自然科学基金资助项目(61472449, 61370172, 61402054)(Projects (61472449, 61370172, 61402054) supported by the National Natural Science Foundation of China)

通信作者：冯启龙，博士，副教授，从事计算机算法研究；E-mail：csufeng@csu.edu.cn