J. Cent. South Univ. (2012) 19: 1249-1257

DOI: 10.1007/s11771-012-1136-9

Fault detection and identification for dead reckoning system of mobile robot based on fuzzy logic particle filter

YU Ling-li(余伶俐), CAI Zi-xing(蔡自兴), ZHOU Zhi(周智), FENG Zhen-qiu(奉振球)

School of Information Science and Engineering, Central South University, Changsha 410083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: To deal with fault detection and diagnosis with incomplete model for dead reckoning system of mobile robot, an integrative framework of particle filter detection and fuzzy logic diagnosis was devised. Firstly, an adaptive fault space is designed for recognizing both known faults and unknown faults, in corresponding modes of modeled and model-free. Secondly, the particle filter is utilized to diagnose the modeled faults and detect model-free fault according to the low particle weight and reliability. Especially, the proposed fuzzy logic diagnosis can further analyze model-free modes and identify some soft faults in unknown fault space. The MORCS-1 experimental results show that the fuzzy diagnosis particle filter (FDPF) combinational framework improves fault detection and identification completeness. Specifically speaking, FDPF is feasible to diagnose the modeled faults in known space. Furthermore, the types of model-free soft faults can also be further identified and diagnosed in unknown fault space.

Key words: fault detection and diagnosis; particle filter; fuzzy logic; hard fault; soft fault

1 Introduction

Accurate fault detection and diagnosis in dead reckoning system plays a crucial role for mobile robot in reducing operating costs and improving safety. Actually, the dead reckoning system is a classic incomplete model hybrid dynamic system [1-2], which contains discrete fault mode and continuous state variable, meanwhile the structure and parameters of all kinds of failure modes are totally different including the normal mode. Due to the system incompleteness, there might be a lot of unknown, inestimable, and model-free fault modes. Therefore, it is necessary to extract available information as much as possible from the unknown or model-free fault space, and enhance fault detecting and identifying efficiency even in model-free modes to improve system reliability.

The problem of fault detection and diagnosis in hybrid dynamic systems has attracted considerable attention worldwide [3-5]. In a broad sense, the methods of fault detection and diagnosis can fall into two major categories: quantitative analysis approach and qualitative analysis approach [6]. The former approach includes data-driven based methods [7] and mathematical-model based methods, while the latter approach consists of graphic theory, and knowledge based techniques etc.

In this work, integration of quantitative and qualitative analysis approaches is carried out; in other words, state estimation of particle filter and knowledge frame of fuzzy diagnosis are integrated to realize fault detection and diagnosis within incomplete hybrid dead reckoning sensor system. As we all know, particle filter is a Monte Carlo technique for monitoring dynamic system through approximating probability distribution with non-parametric weight sample set, which supplies a feasible method for nonlinear, non-Gaussian hybrid state estimation. The method for fault diagnosis in nonlinear and non-Gaussian multi-model hybrid system by particle filter has been presented in Refs. [8-11]. The performance of multi-model estimation is mainly dependent on the system model, which is hypothetically under the conditions of completeness and mutual exclusiveness in most researches recently [12]. Besides, one of the premises to converge the particle filter is that the support set of proposal distribution needs to cover the posterior distribution [13], which is named complete model of the system. Incomplete system, however, is a general practical problem in robot system. Thus, it is much more significant to investigate fault diagnosis in incomplete model [14-15]. An algorithm of particle filter for incomplete model hybrid system has been proposed in Ref. [16] by describing the model-free dynamic state with unknown model-free fault mode, extracting two statistics parameters for particle set, and on this basis, designing logic threshold to detect the unknown faults. In Ref. [17], the state estimation and unknown fault detection are supported by compound weight which is equal to preset transition probability of each mode multiplied by corresponding average weight of different mode particle-set. The above two methods can both detect unknown faults, but underperform in identifying the type of unknown fault. Both methods extract the common ground of all the unknown faults, but do not analyze deeply the disparity shown by all kinds of faults. In actual application, the particle filter can feasibly establish and diagnose the modeled hard fault, but only attribute soft fault and some model-free fault to typical unknown fault space. So, in this work, the study of incomplete model fault diagnosis of dead reckoning system is conducted, and more fault types of incomplete fault space are analyzed and identified, especially, more information about soft faults in model-free fault space is extracted. To achieve hard fault diagnosis of modeled fault space and simultaneously detect the unknown fault within incomplete model-free fault space, a combinational framework is proposed, where the particle filter diagnoses modeled sensor hard faults and detects model-free faults, and fuzzy logic combining the former identifies the types of corresponding soft faults further even in unknown model-free fault space like wheels slip and a gyroscope gripping.

2 Fault diagnosis system in dead reckoning for mobile robots

The expression of hybrid dynamic system (HDS) is

                        (1)

where S_t∈S, is the discrete system mode at time t; S is the finite set of discrete system modes;  is the multi-variable continuous state of the system at time t; is the measurement of the system at time t; is the input of dead reckoning system at time t; v_t and n_t are considered as the process noise and measurement noise, respectively.

As known to all, fault diagnosis system (FDS) in dead reckoning for mobile robots is a typical FDS with incomplete models. The incomplete models particularly describe the situations that cannot be modeled of dynamic fault mode, unknown fault mode, and kinemics model of mobile robots. It is important for us to understand that the performances of model-free fault mode and the modeled fault mode are materially different [16].

2.1 Analysis on experimental platform MORCS-1

The picture of MORCS-1 is shown in Fig.1, whose dead reckoning system is composed of encoders for the left and right wheels, and the mobile-robot gyroscope. The encoders measure the angular velocity of left and right driving wheels, respectively; meanwhile, the gyro measures the yaw rate of the robot. As the turning is achieved by the different speeds between left and right motors in actual running, the motion pattern is decided by the speed of left and/or right driving wheel. The robot may be in the static mode (M1, ), the straight line mode (M2, ), the rotation mode about the left wheel (M3, ), the rotation mode about the right wheel (M4, ), and other rotation mode (M5, ). The mobile robot motion pattern is subjected to the detectable fault state set of one sensor. For example, it is difficult to check the sensor fault when the robot is stationary as the outputs of encoders and gyro are zero; similarly, the fault of gyro is hard to find when the robot is in straight line mode (M2).

Fig. 1 MORCS-1 mobile robot

2.2 Definitions of hard and soft fault in dead reckoning sensor system

The faults of sensor in dead reckoning system include hard faults, soft faults and other kind of faults, where the hard and soft fault definitions are as follows:

Definition 1: Hard fault means that the sensor loses its function completely, characterized by fixed outputs of acquired data of the fault sensor, or distinct step change in measured value when it happens. Hard fault can be modeled for particle filter.

Definition 2: Soft fault means drop in sensor performance which may be caused by noise or abnormal output gains, such as noise hybrid fault [18], and scale factor fault [19]. The symptom is not obvious at first, but it would be more and more distinct as time goes on. Soft fault is hard to model for particle filter due to the acquired disordered data of fault sensor, so soft faults are always attributed to unknown fault space.

2.3 Adaptive fault space

An adaptive fault space is designed in this work which is mainly divided into two parts: the known and unknown fault mode spaces, as shown in Fig. 2. The modeled modes of hard faults and normal state are attributed to known fault space, and the soft faults of model-free modes always fall into unknown fault space, because they take on the unknown characteristics in particle filter. Besides, the unknown fault space includes some other model-free fault modes. So, it would be in known fault space S when hard fault occurs or in normal mode (shown in the left part of Fig. 2). While the unknown fault is detected, the fault space would extend to {S, S_s, S_u} adaptively for improving the accuracy of fault diagnosis.

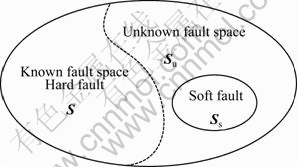
Fig. 2 Adaptive fault space with soft faults

Definition 3: The known fault mode space S is the set of all the modeled fault modes, including normal modes and all kinds of modeled hard fault modes, and S={s|Dynamic model has been confirmed}.

Definition 4: The unknown fault mode space generally refers to model-free fault mode sets with different dynamic performances compared to the known modes. S_u is used to represent all the unknown mode sets in the right part of Fig. 2. It includes model-free soft faults and the other model-free fault modes.

In this work, we mainly research the soft faults attached to unknown fault space which is a subset of unknown fault space. The known fault space of MORCS-1 dead reckoning system is composed of one normal mode and seven hard fault modes (hard faults in left encoder, right encoder, gyro, left and right encoders, left encoder and gyro, right encoder and gyro, left and right encoders and gyro). There are a variety of unknown fault modes and causes, for example, when a soft fault caused by abnormal output is gained, it may be detected as unknown fault, because the scale factor is difficult to model in the particle filter algorithm. Compared with other fault modes, the particle weight of real fault is larger than the weight of any other fault states, so FDS diagnoses the hard fault efficiently because of the step change in hard fault. On the contrary, gradual change in soft fault makes the outputs in the effective region and the particles with low weights. It is not easy to diagnose the real fault, so the PF algorithm can only detect it as the unknown fault mode yet cannot diagnose the type of model-free fault.

2.4 Improved method: Fuzzy diagnosis for type of soft fault

DUAN et al [11, 16, 20-21] diagnosed sensor hard fault and detected unknown soft fault effectively, but they were unable to classify the type of model-free soft fault in unknown space. Because of the trends of step change in sensor hard fault, the mode of normal/hard fault can be estimated according to the particle weights derived from the error between measured outputs of sensors and given values. However, the measured outputs of soft fault are in a region between the normal and hard fault values, and there is no corresponding mode of soft faults in incomplete models of particle filter, resulting in the fact that the weight and reliability of each particle are all extremely low when soft fault takes place.

If we add some soft fault modes into particle filter directly to deal with the incomplete model problem, it would bring into probably worse fact that the total number of modeled fault modes would exponentially increase. In the other word, there would be many fault modes if various modes of soft fault types are added to the incomplete models of particle filter. Meanwhile, we all know that the weights of particles would exponentially decrease along with increasing the error between measurements and given values, leading to a limited output region of soft faults which can be detected as a soft fault mode. Thus, it is difficult to establish corresponding models for sensor soft faults, or to diagnose soft faults of sensors. In Fig. 3(a), hard fault could be detected and identified by the particle filter if the measured output is 0 or m_nor. Detected fault could only be diagnosed as unknown fault if measured output is in region of [0, m_nor], in which there are no soft fault modes. In Fig. 3(b), if the corresponding modes of soft faults need to be established, many modes should be built for each sensor soft fault due to the characteristics of particle filter, and then we can detect all kinds of probable modeled hard and soft faults. However, it is not a very wise way.

In summary, sensor soft fault can only be detected, but not be diagnosed by particle filter, and the space of sensor soft fault is real subspace of unknown fault modes. Therefore, an algorithm of particle filter based on fuzzy diagnosis is proposed in this work, which can diagnose sensor soft fault by analyzing more information of the unknown fault space, and it modulates the unknown fault space adaptively and achieves detection and diagnosis in incomplete model of soft faults.

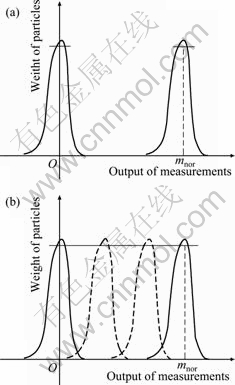
Fig. 3 Diagram of hard (a) and soft (b) fault modes

3 Fuzzy diagnosis particle filter (FDPF) algorithm

3.1 Fuzzy relations

Fuzzy fault diagnosis uses membership functions and fuzzy relation matrix in the fuzzy set theory to describe the fuzzy relations between faults and symptom sets, and to detect and diagnose faults. Then, the fuzzy model of fault diagnosis system is established. Set Ψ={ψ₁, ψ₂, …, ψ_n} as all types of reasons of faults, where n is the total number of the reason types. Set  as all types of symptoms caused by n reasons, where m is the total number of the symptom types. Due to the fuzziness of symptom bounds, membership functions need to be built to represent the membership degrees of fault reasons. Set the observed symptom sample set as (ξ₁, ξ₂,…, ξ_m), and use fuzzy vector  to represent the membership degree of each element ξ_i to symptom . Suppose that the symptom sample is caused by the reason ψ, with the membership degree  to all types of reasons, similarly, vector   should be used to represent the fault reasons. According to the compositional rule of fuzzy inference, the causality of the symptoms to their reasons can be represented by equation , where  is the fuzzy diagnosis membership matrix:

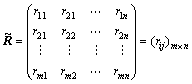              (2)

In the m×n matrix, rows express fault symptoms, and columns express fault reasons. The element r_ij∈[0,1] (i=1, 2, …, m; j=1, 2, …, n) indicates the membership degree of the i-th symptom to the j-th reason, namely r_ij=μ_yj(x_i). Thus, the fuzzy relation function can be represented by

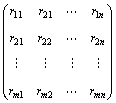                          (3)

For a certain system, based on compositional rule of fuzzy inference, fuzzy vector  of fault reasons can be derived according to the observed fault symptom sample set (ξ₁, ξ₂, …, ξ_m) and fuzzy membership matrix . As a result, the faults can be diagnosed synthetically.

3.2 Identification of fault reasons

The “” in  is fuzzy fault diagnose

operator,  which  specifically  is  

,  j=1, 2, …, n. Not only does this

operator consider all factors, but also preserves the factor evaluations, so every factor and causality will be taken into account. By compositional operation of  and , the fuzzy vector of fault reasons ={ψ₁, ψ₂,…, ψ_n} can be derived, which means the membership degree of sample data to fault reasons.

3.3 Extraction of fault symptoms

For MORCS-1, there are features of both left and right encoders (one is given value, and the other is measured value). The feature of gyro is its measured output, and yaw rate can be calculated according to left and right encoders. Consequently, three fault symptoms can be extracted. In Table 1,  and  indicate the fault symptom of left wheel, right wheel, and gyro; and indicate the given inputs; and indicate the outputs, respectively; γ is a coefficient. The value of fault symptom is zero if there is no fault.

Table 1 Fault symptoms

3.4 Fuzzification of fault symptoms

Since the symptom value would not be certain in a region, the symptom should be fuzzified, in which the key is to select the membership function properly. Based on the characteristics of soft faults, the larger the symptom value is, the larger possible the corresponding soft fault will be. If the symptom value is greater than a certain threshold, assumption would be made that the possibility of it being soft fault is 1.

3.5 Fault reason set and fuzzy diagnosis matrix

The combination of three sensors is seven soft faults, so, the fault reason set is {S_s2, S_s3,…, S_s8}. The fuzzy diagnosis matrix, with three symptoms and seven reasons, is a 3×7 matrix, expressing the corresponding relation between the symptoms and reasons.

3.6 Implementing process of fuzzy diagnosis

Based on the above analysis, the implementing process of fuzzy diagnosis algorithm is as follows: 1) Establish the fuzzy diagnosis membership matrix  indicating the relation between faults and symptoms; 2) Measure the symptom parameter vector of the object; 3) Solve the function; 4) Calculate the fault vector ; 4) Determine the reason from the fault vector and arrive the diagnosis result.

3.7 Description of FDPF algorithm

Step 1: Initialization

1) Set the number of particles N, parameters α and β, and fault diagnosis matrix R. The mode space is S, and prior distribution is P(s₀), and transition probability is

2) Sample the discrete state  from the prior distribution P(s₀);

3) Sample the continuousfrom the prior distribution .

In every step time t, recursively predict, update, estimate, detect unknown faults and resample the particle set.

Step 2: State estimation (importance sampling)

1) Extract discrete samples, ~

according to the transition probability of discrete state;

2) Extract samples ,

according to the transition probability of continuous state defined by discrete state of samples.

Step 3: Weights updating

1) Calculate un-normalized weights ,

;

2) Calculate normalized factor ;

3) Normalize weights ;

Step 4: State estimation

                   (4)

Step 5: Statistics calculation

                    (5)

Step 6: Unknown fault detection

If W_t<α and , move to Step 7; if else, skip Step 7.

Step 7: Get into unknown fault diagnosis

1) Extract the value of fault symptom, ξ=γ(u_t-z_t), including and with their representations as mentioned above. The value of fault symptom is zero if there is no fault.

2) Fuzzify the fault symptoms, , and get the fuzzy vector of symptoms:

Due to the characteristic of soft faults, the larger the symptom value is, the larger possible the corresponding soft fault will be. If the symptom value is greater than a certain threshold, assumption is made that the possibility of it being soft fault is 1.

3) Combine the fuzzy symptom vector and fuzzy diagnosis membership matrix, to calculate the fuzzy fault reason vector;

4) Determine the fault type ψ=max(), based on the maximum membership degree principle.

Step 8: Resampling

1) Generate the new sample particle set , and ;

2) Update the particle set and weights,

Since the weight and reliability of all particles are low in sensor soft faults, the algorithm will move to Step 7 as long as the soft fault occurs, so different membership functions should be designed, respectively, aimed at hard and soft faults. As shown in Fig. 4, if the value of symptom is small, the system will be in normal state; if the value is in [m1, m2], the membership degree of soft fault (dotted line) will be greater than that of hard fault (solid line), and the value will be closed to 1; if the value is greater than m2, the result will go to the opposite.

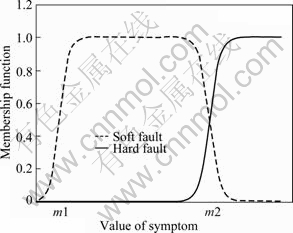
Fig. 4 Diagram of membership function

4 Analysis and simulation platform

4.1 Analysis of experimental results

MORCS-1 [22] is utilized as our experimental platform, and data of each sensor are shown in Fig. 5,

Fig. 5 MORCS-1 experimental data of each sensor: (a) Left wheel setting/given velocity; (b) Left wheel measured velocity; (c) Right wheel setting/given velocity; (d) Right wheel setting/given velocity; (e) Theoretical value of gyro; (f) Measured value of gyro; (g) Type of moving modes

Due to those collected data, we can analyze soft/hard or other faults using FDPF algorithm for the dead reckoning system of MORCS-1.

The FDPF algorithm mainly consists of two parts: detection and diagnosis of PF for modeled fault modes, and fuzzy diagnosis for model-free modes in unknown fault space. The dead reckoning results of each diagnosis are shown in Fig. 6, and the types of faults are shown in Table 2. Figure 6(a) shows the diagnosed results of normal condition (y=1) and hard faults (y=2, 3, …, 8, meaning hard faults in left encoder, right encoder, gyro, left and right encoders, left encoder and gyro, right encoder and gyro, left and right encoders and gyro). Even if only one sensor had a soft fault, the PF could not work well, and the sorted result would be model-free modes in unknown fault space, and its soft fault type should be confirmed by fuzzy logic diagnosis. “y=0” in

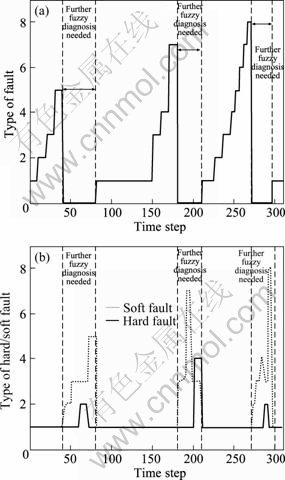
Fig. 6 Diagnosis result with FDPF algorithm: (a) Detection and diagnosis of particle filter; (b) Fuzzy fault diagnosis

Table 2 Code for fault

Fig. 6(a) indicates the state of model-free modes in unknown fault space, and it needs identification and diagnosis further by fuzzy logic. Meanwhile, it may be replace by “y=1” in Fig. 6(b) if only hard faults occurs. Once the soft faults happen, the fuzzy logic would start to detect and diagnose simultaneously the hard and soft faults types. As illustrated in Fig. 6, the sensors are in normal state of time step 1-9; only left encoder has hard fault in time step 10-20; and in time step 201-210, there are concurrent faults, both hard and soft, so the result is “y=0” (unknown faults) in Fig. 6(a), while “soft fault in right encoder and hard fault in gyro” in Fig. 6(b).

A comparison was carried out to validate the efficiency of FDPF. Figure 7(a) shows the divergent results of general particle filter (GPF), which misdiagnose the soft faults by random fault state. Figure 7(b) shows that the results of particle filter for incomplete models (PFIM) [16] are the same with those of FDPF if and only if the known hard fault occurs, but PFIM cannot diagnose the soft faults or hybrid fault in unknown fault space, while FDPF, with fuzzy logic diagnosis integrating into PF, can diagnose model-free faults in part of dead reckoning incomplete model, as shown in Fig. 7(c). As stated previously, FDPF has its superiority in identifying sensors soft faults of model-free unknown fault space, giving the details of soft fault types. However, GPF turns out divergent, and PFIM can only detect the unknown faults with less power for diagnosing and identifying the soft fault types.

4.2 Design of simulation and verification platform

In GUIDE environment, an intuitive and friendly interface is made, as shown in Fig. 8, which includes modules of fault diagnosis result display, sensor data load, and time step selection to check fault type and button.

The diagnosed results by FDPF are displayed in two coordinate systems, and the fault types can be drawn by synthesizing them. The help windows, explaining the exact fault type of each number on y-axis, will pop-up by mousing the left click at any position on the axis. Simultaneous results of GPF and FDPF and all kind of faults are shown respectively in the left of Fig. 8, while results of only FDPF and only soft faults are shown in Fig. 9.

The module of data load is used for loading given and measured values of sensors to compare with the diagnosed results. The diagnosed results are graphically displayed in the graphical display zone; besides that, a non-graphical display is provided in this interface, that is, to select time step to check the corresponding fault type, with the upper half showing the continuous time step and lower half showing the fault type, as shown in the right of Fig. 8.

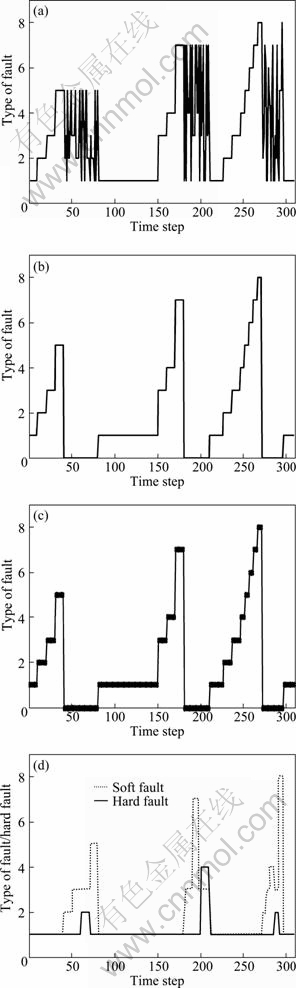
Fig. 7 Comparison results between FDPF and PFIM: (a) GPF; (b) PFIM; (c) and (d) FDPF

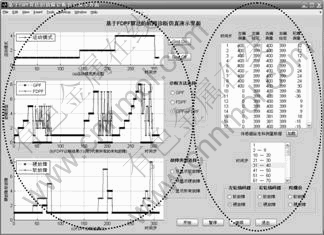
Fig. 8 Graphical user interface

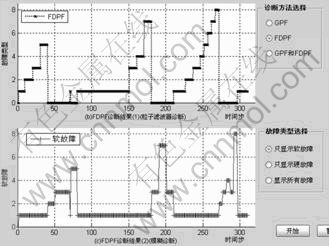
Fig. 9 Graphical display for fault diagnosis result

The button zone includes buttons of start, pause, continue, and exit. The simulation which synchronously displays dynamic diagnosed results is triggered by clicking the start button. The simulation will pause, continue and exit when relevant buttons are pressed.

5 Conclusions

1) An adaptive fault space and a framework of particle filter and fuzzy logic fusion have been designed, and FDPF algorithm has been proposed aiming at soft fault detection and diagnosis in incomplete model system. The adaptive fault space improves the efficiency of fault diagnosis to some extent. The particle filter can diagnose the hard faults and detect model-free fault, and furthermore, the fuzzy logic can diagnose soft faults in unknown space. This diagnosis framework can feasibly detect and diagnose unknown soft faults, and improve the accuracy of fault diagnosis.

2) Some hypotheses have been made, such as only analyzing sampled abnormal data without consideration of mechanical problems, and running the robot in a horizontal vision regardless of pitch angles, which will be difficult issues for further research.

References

[1] MO Yi-wei, XIAO De-yun. Fault diagnosis of hybrid systems based on the evolutionary particle filter [J]. Control and Decision, 2004, 19(6): 611-615. (in Chinese)

[2] MO Yi-wei, XIAO De-yun. Hybrid system monitoring and diagnosing based on particle filter algorithm [J]. Acta Automatica Sinica, 2003, 29(5): 641-648. (in Chinese)

[3] THUMATI B T, JAGANNATHAN S. A model-based fault-detection and prediction scheme for nonlinear multivariable discrete-time systems with asymptotic stability guarantees [J]. IEEE Transactions on Neural Networks, 2010, 21(3): 404-423.

[4] HUANG S, TAN K K. Fault detection and diagnosis based on modeling and estimation methods [J]. IEEE Transactions on Neural Networks, 2009, 20(5): 872-881.

[5] QING W, MEHRDAD S. Robust fault diagnosis of a satellite system using a learning strategy and second order sliding mode observer [J]. IEEE Systems Journal, 2010, 4(1): 112-121.

[6] ZHOU Dong-hua, HU Yan-yan. Fault diagnosis techniques for dynamic systems [J]. Acta Automatica Sinica, 2009, 35(6): 748-758. (in Chinese)

[7] WANG Hong, CHAI Tian-you, DING Jin-liang, BROWN M. Data driven fault diagnosis and fault tolerant control: Some advances and possible new directions [J]. Acta Automatica Sinica, 2009, 35(6): 739-747.

[8] MARSEGUERRA M, ZIO E. Monte Carlo simulation for model-based fault diagnosis in dynamic systems [J]. Reliability Engineering and System Safety, 2009, 94(2): 180-186.

[9] YANG Xiao-jun, PAN Quan, ZHANG Hong-cai. Adaptive multi-model diagnosis using Monte Carlo method [J]. Control Theory and Applications, 2005, 22(5): 723-727. (in Chinese)

[10] REFAN M H, BAHMANPOUR S, BASHOOKI M. A particle filtering-based framework for on-line fault diagnosis in hybrid systems [J]. International Journal of Innovative Computing, Information and Control, 2010, 6(8): 3669-3680.

[11] DUAN Zhuo-hua, CAI Zi-xing, YU Jin-xia. Fuzzy adaptive particle filter algorithm for mobile robot fault diagnosis [C]// Proceedings of the 13th International Conference on Neural Information Processing. Hong Kong, China: Springer, 2006: 711-720.

[12] ZHAO Chao, ZHANG Jun-chang. Fault detection of control system and multi-model estimation method [J]. Systems Engineering and Electronics, 2001, 23(7): 63-65. (in Chinese)

[13] ARULAMPALM M S, MASKELL S, GORDON N, CLAPP T. A tutorial on particle filters for on-line nonlinear/non-Gaussian Bayesian tracking [J]. IEEE Transactions on Signal Processing, 2002, 50(2): 174-188.

[14] MACCALLUM R C. Working with imperfect models [J]. Multivariate Behavioral Research, 2003, 38(1): 113-139.

[15] XU Gui-bin, ZHOU Dong-hua. Fault prediction for nonlinear dynamic system with incomplete measurements [J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2009, 37(S1): 23-27. (in Chinese)

[16] DUAN Zhuo-hua, CAI Zi-xing, YU Jin-xia. Particle filtering algorithm for fault diagnosis of multiple model hybrid systems with incomplete models [J]. Acta Automatica Sinica, 2008, 34(5): 581-587. (in Chinese)

[17] TAFAZOLI S, SUN X H. Hybrid system state tracking and fault detection using particle filter [J]. IEEE Transaction on Control System Technology, 2006, 14(6): 1078-1087.

[18] CHUNG H, OJEDA L, BORENSTEIN J. Sensor fusion for mobile robot dead-reckoning with a precision-calibrated fiber optic gyroscope [C]// Proceedings of the 2001 IEEE International Conference on Robotics and Automation. Seoul, 2001: 3588-3593.

[19] BARSHAN B, DURRANT-WHYTE H F. Inertial navigation systems for mobile robots [J]. IEEE Transactions on Robotics and Automation, 1995, 11(3): 328-342.

[20] CAI Zi-xing, DUAN Zhuo-hua, CAI Jing-feng, ZOU Xiao-bing, YU Jin-xia. A multiple particle filters method for fault diagnosis of mobile robot dead-reckoning system [C]// IEEE/RSJ International Conference on Intelligent Robots and Systems. Alberta, Canada, 2005: 481-486.

[21] DUAN Zhuo-hua, FU Ming, CAI Zi-xing, YU Jin-xia. An adaptive particle filter for mobile robot fault diagnosis [J]. Journal of Central South University of Technology, 2006, 13(6): 689-693.

[22] CAI Zi-xing, ZOU Xiao-bing, WANG Lu, DUAN Zhuo-hua, YU Jin-xia. Design of distributed control system for mobile robot [J]. Journal of Central South University: Science and Technology, 2005, 36(5): 727-732. (in Chinese)

(Edited by YANG Bing)

Foundation item: Project(90820302) supported by the National Natural Science Foundation of China; Project(20110491272) supported by China Postdoctoral Science Foundation of China; Project(2012QNZT060) supported by the Fundamental Research Fund for the Central Universities of China; Project(11B070) supported by the Science Research Foundation of Education Bureau of Hunan Province, China; Project(2010-2012) supported by the Postdoctoral Science Foundation of Central South University, China

Received date: 2011-03-07; Accepted date: 2011-07-06

Corresponding author: CAI Zi-xing, Professor; Tel: +86-731-88877355; E-mail: zxcai@csu.edu.cn