DOI: 10.11817/j.issn.1672-7207.2020.09.020

基于卷积神经网络的大地电磁反演
廖晓龙1,张志厚1,姚禹1,路润琪1,范祥泰1,曹云勇2,冯涛2,石泽玉1
(1. 西南交通大学 地球科学与环境工程学院,四川 成都,611756;
2. 中铁二院地勘岩土工程有限责任公司,四川 成都,610031)
摘要:为了提高大地电磁二维反演精度,提出一种基于卷积神经网络的大地电磁反演方法。具体实现步骤如下:首先,对不同模型进行二维正演构建样本数据集;其次,将视电阻率和相位数据作为双通道网络输入,与其对应的地电模型参数作为输出搭建卷积神经网络框架,并对该网络进行监督学习与调参,从而获取最佳反演网络排列及超参数;最后,利用已训练好的网络对未知地电模型进行反演。通过理论模型检验的方法探讨大地电磁TM模式下多种地电模型体的卷积神经网络反演成像效果,并讨论输入分量和模型体深度对反演效果的影响。研究结果表明:本文提出的反演方法能对地电模型实现精准定位与成像,“聚焦”效果比最小二乘反演的优;同时,视电阻率和相位联合反演结果优于单一参量反演结果,浅部模型体的反演结果比深部模型体的优,并且联合反演的均方误差是单一反演的30%~50%。实测结果验证了所提出方法的有效性。
关键词:大地电磁;非线性反演;卷积神经网络
中图分类号:P631 文献标志码:A 开放科学(资源服务)标识码(OSID)
文章编号:1672-7207(2020)09-2546-12
Magnetotelluric inversion based on convolutional neural network
LIAO Xiaolong1, ZHANG Zhihou1, YAO Yu1, LU Runqi1, FAN Xiangtai1, CAO Yunyong2,FENG Tao2, SHI Zeyu1
(1. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University,Chengdu 611756, China;
2. China Railway Eryuan Geotechnical Engineering Co. Ltd., Chengdu 610031, China)
Abstract: In order to improve the accuracy of two-dimensional magnetotelluric inversion, a new method based on convolution neural network was proposed. The specific implementation steps were as follows. Firstly, the sample data set was obtained by two-dimensional forward modeling of different geoelectric models. Then, the convolutional neural network framework was constructed where the inputs were of apparent resistivity and phase and the outputs were corresponding geoelectric model parameters. And the network was supervised and adjusted to obtain the optimal inversion network arrangement and hyperparameter. Finally, the trained network was verified through the inversion of unknown geoelectric model. The effect of convolution neural network inversion of various geoelectric model bodies with TM mode, and the influence of input component and model body depth on the inversion effect were discussed. The results show that the inversion method proposed in this paper can realize accurate positioning and imaging of geoelectric model, and the "focusing" effect is better than that of the least square inversion. Meanwhile, the joint inversion results of apparent resistivity and phase are better than those of the single parameter inversion. the inversion effect of shallow model body is better than that of deep part, and the mean square error of joint inversion is 30%-50% of single inversion. The validity of the new method is verified by the measured results.
Key words: magnetotelluric(MT); nonlinear inversion; convolutional neural network
大地电磁测深是一种利用天然交变电磁场研究地球电性结构的地球物理勘探方法,具有勘探深度大、不受高阻屏蔽、对低阻层反应灵敏等优点,已经广泛运用于矿产油气勘探、地热资源勘查和环境工程等领域[1]。反演是大地电磁数据处理过程中的一类重要技术,已有的大地电磁反演方法如OCCAM反演[2]、快速松弛反演(RRI)[3]、非线性共轭梯度反演(NLCG)[4]及其改进的REBOCC反演[5]、SBI反演[6]、自适应正则化反演[7]、最小二乘正则化反演[8-9]、三维快速松弛反演[10]等,都在大地电磁资料处理与解释中发挥着重要作用,但此类方法对初始模型的依赖性较强,当目标为多峰值的复杂函数时,反演容易陷入局部极小,在一定程度上影响反演的精确性和稳定性。近年来,一些基于神经网络模型的非线性反演方法在地球物理数据处理中受到研究者的极大关注[11],此类方法不依赖初始模型的选取,无需计算灵敏度矩阵,具有良好的全局寻优性能,如:徐海浪等[12]采用神经网络实现了直流电法二维电阻率反演;李创社等[13]将BP神经网络应用于瞬变电磁勘探;耿美霞等[14]采用RBF神经网络反演二维重力密度分布;王鹤等[15]搭建了BP神经网络模型并用遗传算法进行优化,实现了遗传神经网络的大地电磁二维反演;戴前伟等[16]将BP神经网络与粒子群算法结合,应用于电阻率成像非线性反演。以上研究表明神经网络能够以一定精度逼近地球物理参数与介质参数模型之间的数学关系,但这些研究均是基于浅层神经网络模型,在一些更加复杂的非线性特征映射问题上逼近能力仍有不足。针对这一问题,HINTON等[17]提出了深度神经网络(deep neural networks,DNN)模型,DNN在特征提取和建模上有明显的优势,能够从原始的输入数据中挖掘出更深层次的特征,具有超强的复杂函数逼近性能。各种类型的深度网络在断层检测[18-19]、地震相分类[20]、数字岩石物理[21-22]等方面展现出广阔的应用前景。卷积神经网络(convolutional neural networks,CNN)作为深度神经网络的一种类型,其局部连接、权值共享及池化操作等特性可有效降低网络复杂度,提高网络模型的鲁棒性和容错能力[23]。目前,CNN在地球物理领域的应用已经取得一些研究成果,如:林年添等[24]将CNN运用于地震油气储层的预测;奚先等[25]研究了基于CNN的地震偏移剖面中散射体的定位和成像;何旭等[26]利用CNN识别测井相;BI等[27]通过CNN对微震波形进行自动识别;PUZYREV[28]利用CNN实现了特定装置的可控源电磁的二维反演。以上研究表明CNN在地球物理领域具有较大应用潜力,但这些研究大部分集中在地震方面,在电磁方面运用尚少。为此,本文作者提出一种基于CNN的大地电磁反演方法,此方法完全非线性,不会产生传统线性反演方法出现的问题,通过给定观测值(视电阻率、相位)就能立刻对模型参数进行反演。其步骤为:首先阐述CNN的基本原理,介绍利用CNN实现大地电磁反演的基本步骤,然后对理论模型进行反演测试,并讨论不同输入分量以及深度对反演效果的影响,最后通过实测结果验证此方法的有效性。
1 方法原理
1.1 CNN基本原理
20世纪60年代,HUBEL等[29]在研究猫脑皮层中用于方向选择和局部敏感的神经元时,发现其独特的网络结构可以有效地降低反馈神经网络的复杂性,继而提出了CNN。近年来,随着迁移学习理论[30]在CNN上的成功应用,CNN的应用领域得到了进一步扩展[31-32]。目前,CNN已成为当前最受关注的研究热点之一[33]。
CNN具体结构如图1所示,由输入层、卷积层、池化层、全连接层及输出层组成,卷积层和池化层一般取值若干并且交替设置,即1个卷积层连接1个池化层,池化层后再连接1个卷积层。以下介绍CNN的各组成部分。
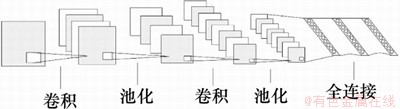
图1 CNN示意图
Fig. 1 Schematic diagram of CNN
1.1.1 卷积层
卷积层由多个特征面组成,每个特征面由多个神经元组成,它的每一个神经元通过卷积核与上一层特征面的局部区域相连。卷积层通过卷积操作提取输入的不同特征,第一层卷积层提取低级特征如边缘、线条、角落,更高层的卷积层提取更高级的特征[23]。卷积过程如图2所示。前一层的特征图与一个可学习的卷积核(卷积核实际是一个权值矩阵[34])进行卷积,再加上偏置,然后通过激活函数激活,最后得到输出特征图。每一个特征输出图可以组合多个特征卷积图,卷积计算公式如下:
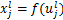 (1)
(1)
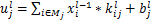 (2)
(2)
式中: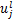 为卷积层
为卷积层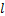 第
第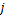 个通道的净激活输出,它是通过对前一层输出的特征图
个通道的净激活输出,它是通过对前一层输出的特征图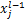 进行卷积求和与偏置操作后得到的;
进行卷积求和与偏置操作后得到的;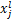 为卷积层
为卷积层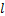 第
第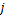 个通道的输出;
个通道的输出; 为激活函数;
为激活函数;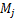 为特征图子集;
为特征图子集;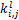 为卷积核;
为卷积核;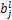 为卷积层的偏置项;“*”为卷积符号。
为卷积层的偏置项;“*”为卷积符号。
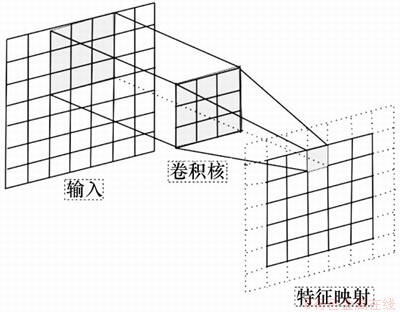
图2 卷积示意图
Fig. 2 Schematic diagram of convolution
1.1.2 池化层
池化层在卷积层之后,同样由多个特征面构成,它的每一个特征面与卷积层的特征面相对应,且池化层的神经元与其输入层的局部接受域相连,不同神经元的局部接受域不重叠。池化层通过降低特征面的分辨率来获得空间不变性特征,降低网络的规模,同时起到提取二次特征的作用,常用的池化方法有平均池化(mean-pooling)、最大池化(max-pooling)等[35],池化的过程可由以下公式描述:
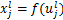 (3)
(3)
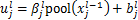 (4)
(4)
式中: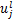 为池化层
为池化层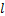 第
第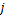 个通道的净激活输出,通过前一层的特征图
个通道的净激活输出,通过前一层的特征图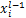 池化加权、偏置后得到;
池化加权、偏置后得到;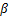 为池化权重系数;
为池化权重系数;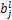 为池化层的偏置项;
为池化层的偏置项;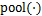 为池化函数。
为池化函数。
1.1.3 全连接层
在CNN结构中,全连接层位于卷积层与池化层之后,它的每一个神经元与前一层神经元完全连接,可以整合卷积层或池化层中具有类别区分的局部信息,全连接层的计算过程如下:
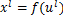 (5)
(5)
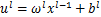 (6)
(6)
式中: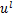 为全连接层
为全连接层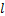 的净激活输出,由前一层的输出加权求和偏置后得到;
的净激活输出,由前一层的输出加权求和偏置后得到;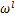 为全连接网络的权值系数;
为全连接网络的权值系数;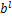 为全连接层的偏置项。
为全连接层的偏置项。
1.1.4 激活函数
激活函数在神经网络信息传递过程中具有十分重要的作用,若不采用激活函数,则每一层的输入将是上一层输出的线性函数,网络的逼近能力将非常有限。因此,常采用一些非线性函数作为激活函数,这样,神经网络就能拥有更强大的非线性映射能力。常用激活函数有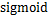 函数、
函数、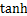 函数和
函数和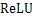 函数,数学形式如下:
函数,数学形式如下:
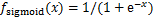 (7)
(7)
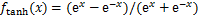 (8)
(8)
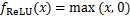 (9)
(9)
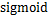 函数能够将输入的连续实值变换为0和1之间的输出,
函数能够将输入的连续实值变换为0和1之间的输出,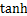 函数能够将变量映射到-1到1之间。对于
函数能够将变量映射到-1到1之间。对于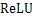 函数,当输入大于0时,输出等于输入,否则输出为0。与
函数,当输入大于0时,输出等于输入,否则输出为0。与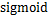 函数和
函数和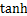 函数相比,
函数相比,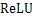 函数能够解决梯度消失等问题,还能加快收敛速度,因此,在目前的CNN结构中,常用
函数能够解决梯度消失等问题,还能加快收敛速度,因此,在目前的CNN结构中,常用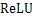 函数作为激活函数。
函数作为激活函数。
1.2 基于CNN的大地电磁反演实现步骤
首次将CNN运用于大地电磁反演。目前CNN的主要应用集中在图像识别、目标检测等领域[36-37],处理的目标通常是图像,网络的输入为像素点。在地球物理领域,采集的某一个观测数据理论上可以看作1个像素点,因此,本文将大地电磁视电阻率及相位看作不同颜色通道的像素点,作为卷积神经网络的输入,将地电模型参数作为网络的输出,将CNN运用于大地电磁反演。实现流程如图3所示,具体实施步骤如下。
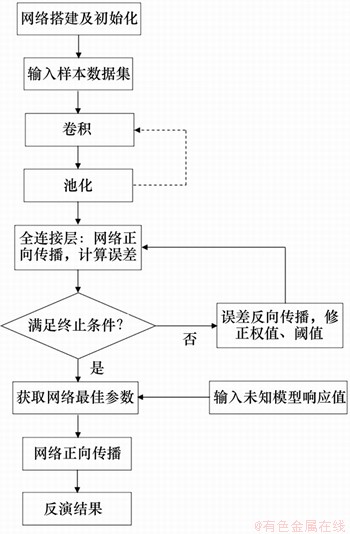
图3 基于CNN的大地电磁反演流程图
Fig. 3 Flow chart of MT inversion based on CNN
1) CNN搭建及初始化。依据待解决问题搭建CNN基本框架,采用小随机数(均值为0,方差为0.01的高斯分布)对网络的权值与偏置进行初始赋值。
2) 样本数据集构建及输入。通过大地电磁二维正演获取样本数据集,正演方法采用有限单元法[38]。为提高计算效率与精度,对网格进行双二次插值,并将整个网格划分为2个区域:目标区域和网格外延区域。目标区域为地质体的赋存区域,同时也是数据采集区域,以均匀网格剖分;网格外延区域的网格步长按二倍递增。在目标区域内,地质体按一定步长进行移动,以获取不同位置的视电阻率及相位,并记录相应地电模型参数。采用零-均值归一化方法对数据集进行标准化,将标准化后的视电阻率及相位作为CNN双通道输入,相应模型地电参数作为输出。
3) 卷积。将步骤2)中的输入数据进行卷积处理,即将每一个位置的输入进行卷积变换映射成新值,将卷积核看成权重记为向量w,输入数据记为向量x,则该位置卷积结果为y=w'x+b,即向量内积加上偏置,将x变换为y,然后通过激活函数激活即可得到卷积结果,在此过程中,不同的卷积核将实现数据不同特征的提取。
4) 池化。采用最大池化法对步骤3)中卷积后的数据进行池化处理,即将池化窗口区域内数据的最大值保留,再通过激活函数激活就可得到结果,通过此步骤可对数据体进行降维及二次特征提取。根据本文待解决问题的复杂程度,对数据再次进行卷积操作,即回到步骤3)。
5) 信息正向传播和误差反向传递。CNN在学习训练过程中,通过BP算法进行监督训练,需要通过信息正向传播和误差反向传递2个阶段,此操作在全连接层中进行。在误差正向传播阶段,池化后的数据进入全连接层实现信息的非线性变换,到达输出层;在误差反向传播阶段,网络计算出正向输出与理论值的误差,再计算所有网络层的灵敏度及总误差对所有网络参数的偏导数,从而逐层计算出误差,以修正网络权值与阈值。通过不断的信息正向传播和误差反向传递实现网络训练,当误差达到期望值或迭代次数达到预定值时,网络停止训练,获得最佳反演网络排列及超参数。
6) 模型反演。将学习训练获得的最佳反演网络排列及超参数作为网络的初始赋值,将未知模型响应数据标准化后直接输入网络,通过一次正向传播即可得到输出。
2 CNN大地电磁反演算例
2.1 样本模型选择
在二维大地电磁TM极化模式下,建立地下高阻异常体、低阻异常体、高低阻组合模型、地垒以及地堑5种基础模型,如图4所示。在正演过程中,有限单元法目标区域网格规模设置为35×32,网格间距为200 m。为减少计算量,控制异常体和围岩电阻率不变,通过移动异常体的位置来获取样本数据集,异常体移动位置遍布整个网格,每次移动间距为400 m。计算时,选择36个测点,测点间距为200 m,并记录16个频点的视电阻率及相位,频点范围为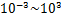 Hz,按对数等间隔分布。将采集范围内所有测点和频点电阻率及相位作为网络输入,则输入为2×36×16的三维数据矩阵;将地电模型参数作为网络输出,则输出层神经元个数为35×32,即1 120个。
Hz,按对数等间隔分布。将采集范围内所有测点和频点电阻率及相位作为网络输入,则输入为2×36×16的三维数据矩阵;将地电模型参数作为网络输出,则输出层神经元个数为35×32,即1 120个。
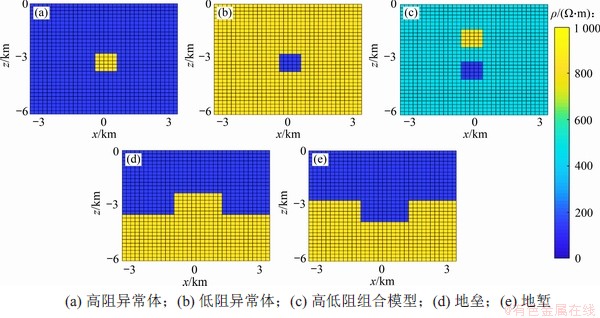
图4 基础地电模型
Fig. 4 Basic geoelectricity models
2.2 网络参数选取
网络参数的选择影响网络的稳定性与反演效果,通过对比试验确定了适合本研究的参数取值,具体参数设置如下:卷积层采用双卷积结构,第一卷积层含卷积核32个,第二卷积层含卷积核64个,池化层均采用最大池化法,全连接层设计为2层,神经元节点数均为1 000个;设置网络训练次数为200轮,损失函数采用均方误差函数,训练过程中使用Adam优化算法[39]进行优化,并采用RELU激活函数与节点丢弃技术防止梯度弥散和过拟合现象。
2.3 模型反演结果
本文就大地电磁TM模式下高阻异常体、低阻异常体、高低阻组合模型、地垒和地堑进行反演测试,设定理论模型与反演结果的均方误差为反演模型评价指标,均方误差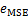 表达式如下:
表达式如下:
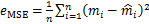 (10)
(10)
式中: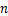 为反演参数个数;
为反演参数个数;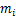 为归一化后测试模型电阻率参数理论值;
为归一化后测试模型电阻率参数理论值;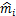 为归一化反演电阻率。
为归一化反演电阻率。
将高阻异常体和高低阻组合模型的CNN反演结果与最小二乘反演结果进行对比,并采用高阻异常体和地垒模型讨论输入分量对反演效果影响,采用低阻异常体和地堑模型探索深度对反演效果的影响。
2.3.1 CNN与基于光滑约束的最小二乘反演对比
选择高阻异常体和高低阻组合模型的CNN反演结果与基于光滑约束的最小二乘反演结果进行对比,基准模型示意图如图4(a)和(c)所示。用作反演的高阻异常体电阻率为1 000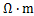 ,长度和宽度均为1.0 km,背景电阻率为100
,长度和宽度均为1.0 km,背景电阻率为100 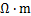 ,异常体中心点在水平方向位置0 km处,埋深3.2 km;高低阻组合模型高阻异常电阻率为1 000
,异常体中心点在水平方向位置0 km处,埋深3.2 km;高低阻组合模型高阻异常电阻率为1 000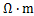 ,低阻异常电阻率为100
,低阻异常电阻率为100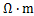 ,长度和宽度均为1.0 km,背景电阻率为500
,长度和宽度均为1.0 km,背景电阻率为500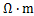 ,高阻异常体中心点在水平方向0 km处,埋深为2.0 km,低阻异常体中心点在水平方向0 km处,埋深为3.8 km。
,高阻异常体中心点在水平方向0 km处,埋深为2.0 km,低阻异常体中心点在水平方向0 km处,埋深为3.8 km。
图5(a)所示为高阻异常体CNN反演结果,图5(b)所示为高阻异常体最小二乘法反演结果,图6(a)所示为高低阻组合模型CNN反演结果,图6(b)所示为高低阻组合模型最小二乘法反演结果,其中,红线代表真实高阻模型位置,蓝线代表真实低阻体位置。从图5和图6可见:最小二乘法反演结果收敛程度较差,对模型体边缘反映不够清晰,而CNN反演方法能较准确地反映异常体的位置、大小和电阻率,能较清晰地刻画模型体的边缘。
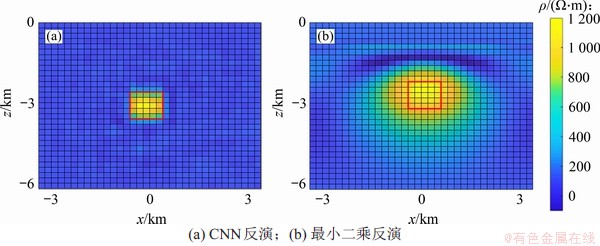
图5 高阻异常体不同方法反演结果
Fig. 5 Inversion results of high-resistance anomaly using different methods
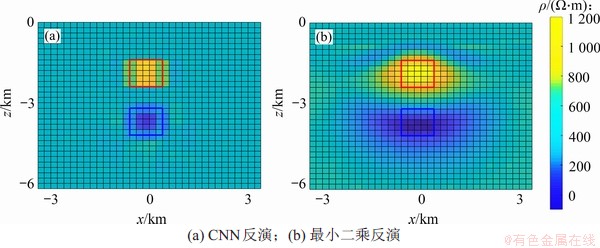
图6 高低阻组合模型不同方法反演结果
Fig. 6 Inversion results of high-low resistance model using different methods
2.3.2 反演结果的正演拟断面图对比分析
将2.3.1节中的单一高阻异常体和高低阻组合模型CNN反演结果进行正演,图7所示为高阻异常体理论正演拟断面图和CNN反演结果的正演拟断面图,图8所示为高低阻组合模型理论正演拟断面图和CNN反演结果的正演拟断面图。从图7和图8可见:无论是反演结果的拟合视电阻率还是阻抗相位,都与其理论的正演结果基本吻合,说明了此反演方法的准确性;值得一提的是,在视电阻率对比结果中,这2种模型的反演拟合视电阻率与理论视电阻率在各个频段均有一定差异;而在相位对比结果中,低频部分的反演拟合相位与理论相位差异并不大,说明相位在低频段的反应并不灵敏。
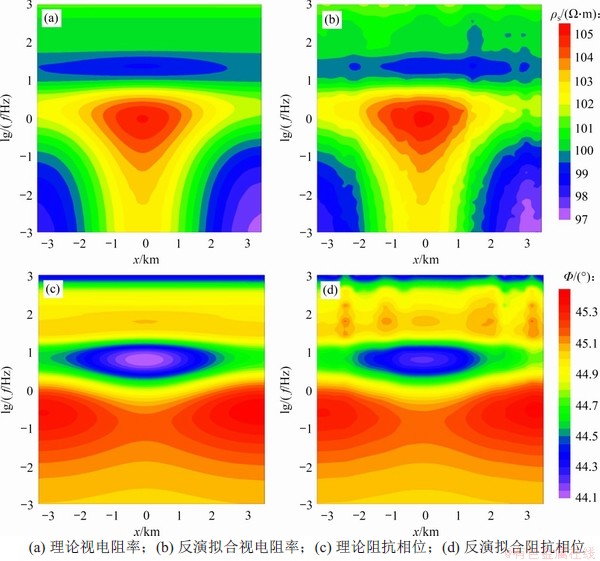
图7 高阻异常体理论正演结果与CNN反演结果的正演结果对比
Fig. 7 Comparison between forward data of theoretical high-resistance anomaly and forward data of CNN inversion results
2.3.3 不同输入分量反演结果对比
选择高阻异常体和地垒模型讨论不同输入分量对反演效果的影响。输入分量包括3种模式:视电阻输入、相位输入、视电阻率和相位联合输入。基准模型示意图如图4(a)和(d)所示。用作反演的高阻异常体电阻率为1 000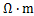 ,长度和宽度均为1.0 km,背景电阻率为100
,长度和宽度均为1.0 km,背景电阻率为100 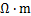 ,异常体中心在水平方向位置0 km处,埋深为2.4 km;地垒模型凸起部分电阻率为1 000
,异常体中心在水平方向位置0 km处,埋深为2.4 km;地垒模型凸起部分电阻率为1 000 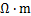 ,长度为1.2 km,宽度为2.0 km,盖层电阻率为100
,长度为1.2 km,宽度为2.0 km,盖层电阻率为100 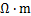 ,凸起部分中心在水平方向位置0 km处,埋深为2.4 km。
,凸起部分中心在水平方向位置0 km处,埋深为2.4 km。
图9(a)和(d)所示为高阻异常体和地垒模型视电阻率和相位联合输入的反演结果,图9(b)和(e)所示为视电阻率输入的反演结果,图9(c)和(f)所示为相位输入的反演结果。从图9可以看出:3种输入模式均取得良好的反演成像效果,相比于单一输入反演,电阻率和相位联合输入的反演结果对边界的刻画更加清晰,更加接近真实模型。表1所示为测试集中10组数据不同输入模式下的均方误差对比,从表1可以看出:高阻异常体模型联合反演的平均均方误差为0.024时,视电阻率和相位反演的平均均方误差分别为0.089和0.090;地垒模型联合反演的平均均方误差为0.035时,视电阻率和相位反演的平均均方误差分别为0.067和0.076。联合反演的均方误差是单一反演的30%~50%,表明视电阻率和相位联合反演具有更好的反演效果。
2.3.4 不同深度反演结果对比
选择低阻异常体和地堑模型探索CNN在不同深度的反演效果,基准模型示意图如图4(b)和(e)所示。用作反演的低阻异常体电阻率为100 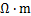 ,长度和宽度均为1.0 km,背景电阻率为1 000
,长度和宽度均为1.0 km,背景电阻率为1 000 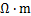 ;地堑模型凹陷部分电阻率为100
;地堑模型凹陷部分电阻率为100 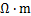 ,长度为1.2 km,宽度为2.0 km;基底电阻率为1 000
,长度为1.2 km,宽度为2.0 km;基底电阻率为1 000 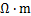 。定义深度[-2,0) km为浅部区域,[-4,-2) km为中部区域,[-6,-4) km为深部区域,若反演模型体中心位于浅部,则将该模型体归为浅部模型体,以此类推。
。定义深度[-2,0) km为浅部区域,[-4,-2) km为中部区域,[-6,-4) km为深部区域,若反演模型体中心位于浅部,则将该模型体归为浅部模型体,以此类推。
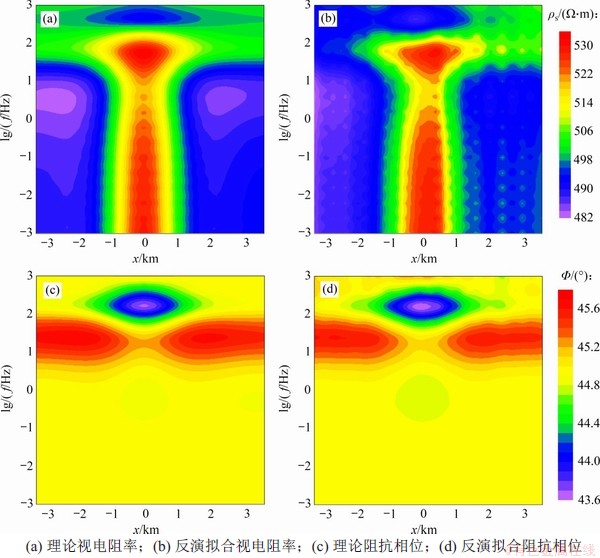
图8 高低阻组合模型理论正演结果与CNN反演结果的正演结果对比
Fig. 8 Comparison between forward data of theoretical high-low resistance model and forward data of CNN inversion results
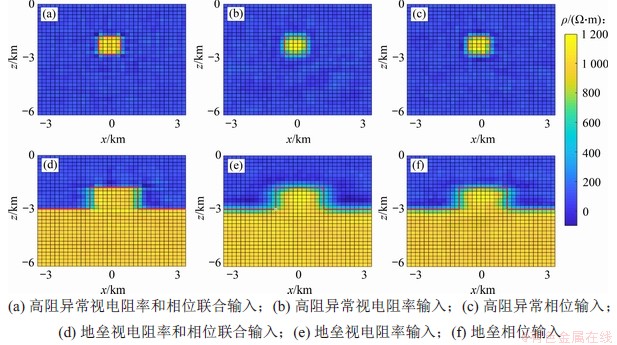
图9 高阻异常和地垒模型不同输入分量反演结果
Fig. 9 Inversion results of different input components of high-resistance anomaly and ground barrier model
从测试集中随机抽取2种模型在不同深度上的反演结果(由于是随机抽取,横向位置与深度均有不同),如图10所示。图10(a),(b)和(c)所示分别为低阻异常体浅部、中部和深部的反演结果,图10(d),(e)和(f)所示分别为地堑模型浅部、中部和深部反演结果,红线代表真实模型界面。从图10可以看出:CNN方法在各个深度处均取得了较好的反演效果,相比于深部,浅部反演模型的效果更好,对异常区域边界刻画更为清晰。表2所示为测试集中10组不同深度反演模型体的均方误差对比。从表2可知:浅、中、深部反演模型的平均均方误差依次增加,说明CNN反演方法对浅部的地质体具有更好的反演效果,随着深度增加,反演效果变差。
表1 不同输入分量反演参数的均方误差对比
Table 1 Comparison of mean square error of inversion results of different input components
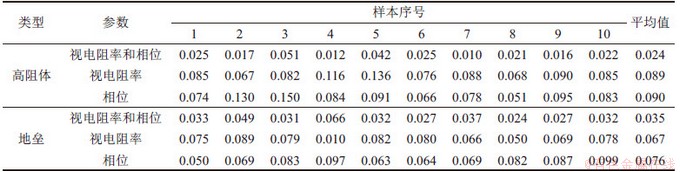
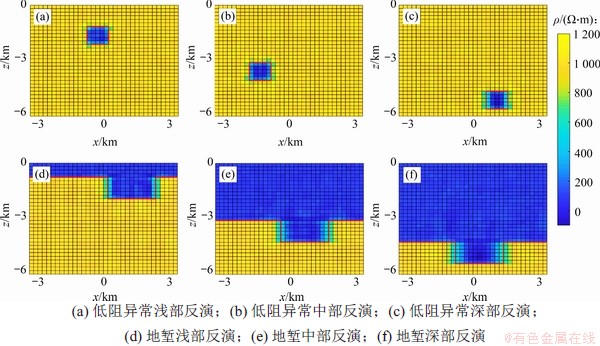
图10 低阻异常和地堑模型在不同深度上的反演结果
Fig. 10 Inversion results of low-resistance anomaly and ground ridge model at different depths
3 实测数据反演
利用CNN方法对云南省云县至凤庆高速公路某隧道的实测电磁参数资料进行反演,采集系统为EM3D,含6个采集通道。经调查,隧道区域附近岩性为前奥陶系石英片岩和绢云母石英片岩。所选测线位于隧道正上方,共布设26个测点,测点间距10 m,记录41个频点,频点范围为2.5~19 983.3 Hz。由于实测数据的频点、点距、电阻率等与理论模型试验不同,需要重新构建样本数据集。首先,根据实际探测区范围构建网格,点距为10 m,所选频点与实测数据频点一致;再根据该地区已知的地质资料和岩石矿物测定结果,确定模型背景电阻率范围为1 000~1 500 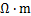 ,异常体电阻率范围100~500
,异常体电阻率范围100~500 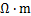 ,通过改变电阻率(按100
,通过改变电阻率(按100 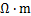 等量改变),同时移动异常体的位置(按20 m等间距移动)来获取样本数据集;然后,将样本数据集放入已搭建的网络(所选参数与2.2节中一致)中进行学习训练;最后,将该地区实测的电阻率与相位作为CNN的双通道输入,通过一次网络正向传播得到输出结果。
等量改变),同时移动异常体的位置(按20 m等间距移动)来获取样本数据集;然后,将样本数据集放入已搭建的网络(所选参数与2.2节中一致)中进行学习训练;最后,将该地区实测的电阻率与相位作为CNN的双通道输入,通过一次网络正向传播得到输出结果。
图11(a)所示为实际资料的CNN反演结果,图11(b)所示为最小二乘反演结果,实线代表隧道位置,虚线代表钻孔位置。2种反演结果均显示隧道50 m处正上方存在低阻异常区域,推测此区域可能存在含水率较高的隐伏破碎带或溶洞,2种反演方法虽然存在一定差异,但反演出的低阻位置大致相符。钻孔资料(ZK1)显示高程2 017~2 050 m为第四系含砾粉质黏土;高程1 867~2 017 m为中等风化云母石英片岩,含水率较高;高程1 823~1 867 m为强风化石英云母片岩,呈松散状,含水率高。采用四极法测定钻孔岩芯电阻率,高程范围1 823~1 867 m内的电阻率明显偏低,与反演结果显示的低阻异常区域吻合,验证了此方法在实际资料反演中的有效性。
表2 不同深度反演结果均方误差对比
Table 2 Comparison of mean square error of inversion results of different depths
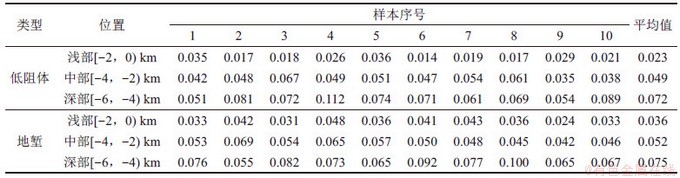
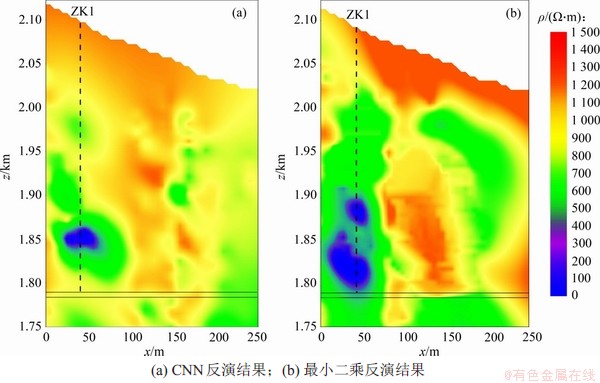
图11 实测资料不同方法反演结果
Fig. 11 Inversion results of measured data by different methods
4 结论
1) 将卷积神经网络引入大地电磁反演,通过数据集建立、模型构建、网络训练和反演测试等步骤实现了地质模型体的精准定位与成像,其“聚焦”反演效果优于最小二乘法。
2) 卷积神经网络的反演效果与输入分量和地电模型深度有关,视电阻率和相位联合反演结果优于单一参量反演结果,浅部模型体的反演结果比深部模型体的优,并且联合反演的均方误差是单一反演的30%~50%。
3) CNN方法在实际资料处理中具有一定实用性,但是目前该方法仅能对简单的地质体进行反演,其主要原因在于样本数据集的泛化性不够,泛化性增加会导致计算量呈几何数量级增加。下一步将对提高模型的泛化性并同时减少计算量进行研究。
参考文献:
[1] 魏文博. 我国大地电磁测深新进展及瞻望[J]. 地球物理学进展, 2002, 17(2): 245-254.
WEI Wenbo. New advance and prospect of magnetotelluric sounding (MT) in China[J]. Progress in Geophysics, 2002, 17(2): 245-254.
[2] CONSTABLE S C, PARKER R L, CONSTABLE C G. Occam's inversion: a practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300.
[3] SMITH J T, BOOKER J R. Rapid inversion of two- and three-dimensional magnetotelluric data[J]. Chinese Journal of Geophysics, 1991, 96(B3): 3905-3922.
[4] RODI W, MACKIE R L. Nonlinear conjugate gradients algorithm for 2-D magnetotelluric inversion[J]. Geophysics, 2001, 66(1): 174-187.
[5] SIRIPUNVARAPORN W, EGBERT G. An efficient data-subspace inversion method for 2-D magnetoyelluric datd[J].Geophysics, 2000, 65(3): 791-803.
[6] DE GROOT-HEDLIN C, CONSTABLE S. Inversion of magnetotelluric data for 2D structure with sharp resistivity contrasts[J]. Geophysics, 2004, 69(1): 78-86.
[7] 陈小斌, 赵国泽, 汤吉, 等. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 2005, 48(4): 937-946.
CHEN Xiaobin, ZHAO Guoze, TANG Ji, et al. An adaptive regularized inversion algorithm for magnetotelluric data[J]. Chinese Journal of Geophysics, 2005, 48(4): 937-946.
[8] LEE S K, KIM H J, SONG Y, et al. MT2DInvMatlab: a program in MATLAB and FORTRAN for two-dimensional magnetotelluric inversion[J]. Computers & Geosciences, 2009, 35(8): 1722-1734.
[9] 冯德山, 王珣. 大地电磁双二次插值FEM正演及最小二乘正则化联合反演[J]. 中国有色金属学报, 2013, 23(9): 2524-2531.
FENG Deshan, WANG Xun. Magnetotelluric finite element method forward based on biquadratic interpolation and least squares regularization joint inversion[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(9): 2524-2531.
[10] 谭捍东, 余钦范, BOOKER J, 等. 大地电磁法三维快速松弛反演[J]. 地球物理学报, 2003, 46(6): 850-854, 889.
TAN Handong, YU Qinfan, BOOKER J, et al. Three-dimensional rapid relaxation inversion for the magnetotell uric method[J]. Chinese Journal of Geophysics, 2003, 46(6): 850-854, 889.
[11] 王家映. 地球物理资料非线性反演方法讲座(五): 人工神经网络反演法[J]. 工程地球物理学报, 2008, 5(3): 255-265.
WANG Jiaying. Lecture on non-linear inverse methods in geophysical data(5): the artificial neural network method[J]. Chinese Journal of Engineering Geophysics, 2008, 5(3): 255-265.
[12] 徐海浪, 吴小平. 电阻率二维神经网络反演[J], 地球物理学报, 2006, 49(2): 584-589.
XU Hailang, WU Xiaoping. 2-D resistivity inversion using the neural network method[J]. Chinese Journal of Geophysics, 2006, 49(2): 584-589.
[13] 李创社, 张彦鹏, 李实, 等. 瞬变电磁勘探中的人工神经网络反演法[J]. 西安交通大学学报, 2001, 35(6): 604-607, 615.
LI Chuangshe, ZHANG Yanpeng, LI Shi, et al. New inversion method of artificial neural network in transient electromagnetic inversion[J]. Journal of Xi'an Jiaotong University, 2001, 35(6): 604-607, 615.
[14] 耿美霞, 杨庆节. 应用RBF神经网络反演二维重力密度分布[J]. 石油地球物理勘探, 2013, 48(4): 651-657.
GENG Meixia, YANG Qingjie. 2-D density inversion with the RBF neural network method[J]. Oil Geophysical Prospecting, 2013, 48(4): 651-657.
[15] 王鹤, 刘梦琳, 席振铢, 等. 基于遗传神经网络的大地电磁反演[J]. 地球物理学报, 2018, 61(4): 1563-1575.
WANG He, LIU Menglin, XI Zhenzhu, et al. Magnetotelluric inversion based on BP neural network optimized by genetic algorithm[J]. Chinese Journal of Geophysics, 2018, 61(4): 1563-1575.
[16] 戴前伟, 江沸菠. 基于混沌振荡PSO-BP算法的电阻率层析成像非线性反演[J]. 中国有色金属学报, 2013, 23(10): 2897-2904.
DAI Qianwei, JIANG Feibo. Nonlinear inversion for electrical resistivity tomography based on chaotic oscillation PSO-BP algorithm[J]. The Chinese Journal of Nonferrous Metals, 2013 23(10): 2897-2904.
[17] HINTON G E. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507.
[18] HUANG Lei, DONG Xishuang, CLEE T E. A scalable deep learning platform for identifying geologic features from seismic attributes[J]. The Leading Edge, 2017, 36(3): 249-256.
[19] WU Xinming, LIANG Luming, SHI Yunzhi, et al. FaultSeg3D: Using synthetic data sets to train an end-to-end convolutional neural network for 3D seismic fault segmentation[J]. Geophysics, 2019, 84(3): IM35-IM45.
[20] SOUZA J F L, SANTOS M D, MAGALHAES R M, et al. Automatic classification of hydrocarbon “leads” in seismic images through artificial and convolutional neural networks[J]. Computers & Geosciences, 2019, 132: 23-32.
[21] MOSSER L, DUBRULE O, BLUNT M J. Stochastic reconstruction of an oolitic limestone by generative adversarial networks[J]. Transport in Porous Media, 2018, 125(1): 81-103.
[22] SUDAKOV O, BURNAEV E, KOROTEEV D. Driving digital rock towards machine learning: Predicting permeability with gradient boosting and deep neural networks[J]. Computers & Geosciences, 2019, 127: 91-98.
[23] 周飞燕, 金林鹏, 董军. 卷积神经网络研究综述[J]. 计算机学报, 2017, 40(6): 1229-1251.
ZHOU Feiyan, JIN Linpeng, DONG Jun. Review of convolutional neural network[J]. Chinese Journal of Computers, 2017, 40(6): 1229-1251.
[24] 林年添, 张栋, 张凯, 等. 地震油气储层的小样本卷积神经网络学习与预测[J]. 地球物理学报, 2018, 61(10): 4110-4125.
LIN Niantian, ZHANG Dong, ZHANG Ka, et al. Predicting distribution of hydrocarbon reservoirs with seismic data based on learning of the small-sample convolution neural network[J]. Chinese Journal of Geophysics, 2018, 61(10): 4110-4125.
[25] 奚先, 黄江清. 基于卷积神经网络的地震偏移剖面中散射体的定位和成像[J]. 地球物理学报, 2020, 63(2): 687-714.
XI Xian, HUANG Jiangqing. Location and imaging of scatterers in seismic migration profiles based on convolution neural network[J]. Chinese Journal of Geophysics, 2020, 63(2): 687-714.
[26] 何旭, 李忠伟, 刘昕, 等. 应用卷积神经网络识别测井相[J]. 石油地球物理勘探, 2019, 54(5): 1159-1165.
HE Xu, LI Zhongwei, LIU Xin, et al. Log facies recognition based on convolutional neural network[J]. Oil Geophysical Prospecting, 2019, 54(5): 1159-1165.
[27] BI Lin, XIE Wei, ZHAO Junjie, et al. Automatic classification of multi-channel microseismic waveform based on DCNN-SPP[J]. Journal of Applied Geophysics, 2018, 159: 446-452.
[28] PUZYREV V. Deep learning electromagnetic inversion with convolutional neural networks[J]. Geophysical Journal International, 2019, 218(2): 817-832.
[29] HUBEL D H, WIESEL T N. Receptive fields, binocular interaction and functional architecture in the cat's visual cortex[J]. The Journal of Physiology, 1962, 160(1): 106-154.
[30] PAN S J, YANG Qiang. A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2010, 22(10): 1345-1359.
[31] COLLOBERT R, WESTON J, BOTTOU L, et al. Natural language processing(almost) from scratch[J]. Journal of Machine Learning Research, 2011, 12(1): 2493-2537.
[32] OQUAB M, BOTTOU L, LAPTEV I, et al. Learning and transferring mid-level image representations using convolutional neural networks[C]// Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition. Washington DC: IEEE Computer Society, 2014: 1717-1724.
[33] 李彦冬, 郝宗波, 雷航. 卷积神经网络研究综述[J]. 计算机应用, 2016, 36(9): 2508-2515, 2565.
LI Yandong, HAO Zongbo, LEI Hang. Survey of convolutional neural network[J]. Journal of Computer Applications, 2016, 36(9): 2508-2515, 2565.
[34] GAO Ligang, CHEN Paiyu, YU Shimeng. Demonstration of convolution kernel operation on resistive cross-point array[J]. IEEE Electron Device Letters, 2016, 37(7): 870-873.
[35] BOUREAU Y L, PONCE J, LECUN Y. A theoretical analysis of feature pooling in visual recognition[J]. International Conference on Machine Learning, 2010, 32 (4) :111-118.
[36] KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]// Proceedings of Advances in Neural Information Processing Systems. Cambridge, MA: MIT Press, 2012: 1106-1114.
[37] ZHANG Xiangyu, ZOU Jianhua, HE Kaiming, et al. Accelerating very deep convolutional networks for classification and detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(10): 1943-1955.
[38] 柳建新, 童孝忠, 郭荣文, 等. 大地电磁测深法勘探: 资料处理、 反演与解释[M]. 北京: 科学出版社, 2012: 48-53.
LIU Jianxin, TONG Xiaozhong, GUO Ronwen, et al. The exploration of magnetotelluric sounding: data processing, inversion and interpretation[M]. Beijing: Science Press, 2012: 48-53.
[39] KINGMA D P, BA J. Adam: a method for stochastic optimization[EB/OL]. [2017-01-30]. https: // arxiv. org/abs/1412. 6980
(编辑 杨幼平)
收稿日期: 2020 -04 -01; 修回日期: 2020 -05 -12
基金项目(Foundation item):四川省科技厅研发项目(2019YFG0001,2017JY0264,2020YFG0303);国家自然科学基金资助项目(41672295) (Projects(2019YFG000, 2017JY0264, 2020YFG0303) supported by the Research and Development Programs of Science and Technology Department of Sichuan Province; Project(41672295) supported by the National Natural Science Foundation of China)
通信作者:张志厚,博士,讲师,从事电磁理论研究;E-mail:logicprimer@163.com