J. Cent. South Univ. (2017) 24: 104-113
DOI: 10.1007/s11771-017-3413-0
Reliability-based robust multi-objective optimization of a 5-DOF vehicle vibration model subjected to random road profiles
Abolfazl Khalkhali, Morteza Sarmadi,Sina Yousefi
Automotive Simulation and Optimal Design Research Laboratory, School of Automotive Engineering,
Iran University of Science & Technology, Tehran 16846-13114, Iran
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: Ride and handling are two paramount factors in design and development of vehicle suspension systems. Conflicting trends in ride and handling characteristics propel engineers toward employing multi-objective optimization methods capable of providing the best trade-off designs compromising both criteria simultaneously. Although many studies have been performed on multi-objective optimization of vehicle suspension system, only a few of them have used probabilistic approaches considering effects of uncertainties in the design. However, it has been proved that optimum point obtained from deterministic optimization without taking into account the effects of uncertainties may lead to high-risk points instead of optimum ones. In this work, reliability-based robust multi-objective optimization of a 5 degree of freedom (5-DOF) vehicle suspension system is performed using method of non-dominated sorting genetic algorithm-II (NSGA-II) in conjunction with Monte Carlo simulation (MCS) to obtain best designs considering both comfort and handling. Road profile is modeled as a random function using power spectral density (PSD) which is in better accordance with reality. To accommodate the robust approach, the variance of all objective functions is also considered to be minimized. Also, to take into account the reliability criterion, a reliability-based constraint is considered in the optimization. A deterministic optimization has also been performed to compare the results with probabilistic study and some other deterministic studies in the literature. In addition, sensitivity analysis has been performed to reveal the effects of different design variables on objective functions. To introduce the best trade-off points from the obtained Pareto fronts, TOPSIS method has been employed. Results show that optimum design point obtained from probabilistic optimization in this work provides better performance while demonstrating very good reliability and robustness. However, other optimum points from deterministic optimizations violate the regarded constraints in the presence of uncertainties.
Key words: probabilistic optimization; vehicle suspension; deterministic optimization; ride; handling; genetic algorithm
1 Introduction
Nowadays, passenger’s comfort is one of the paramount objectives of automakers in design of new products. This factor is highly dependent on how much the vehicle design prevents the exterior noise from entering into the vehicle cabin. The noise can be brought about by different sources such as vehicle braking, acceleration, and road irregularities. A major vehicle subsystem which minimizes the noise in the cabin, is the vehicle suspension system which plays an important role by absorbing acting vibrations on passengers (ride comfort) and providing effective contact between tires and the road surface (road-holding) [1]. However, for evaluating the performance of a vehicle suspension system, one essentially needs to first model the road surface irregularity and roughness as the excitation input.
Due to the road surface irregularities, a vehicle moving along the road is subjected to random excitations. Many efforts have been done by researchers for modeling the road irregularities and roughness (see Ref. [2] for example). Based on classification of International Organization for Standardization (ISO) which is on the basis of the power spectral density (PSD), the road roughness has been divided to grades A to H [3]. Generally, the road excitation input in the space domain is described as a random process, which considers a constant velocity for the vehicle, road excitations can be regarded as a stationary random process [4]. The method of stationary random vibration has been employed by many researchers for examining the vibrational response of the vehicle [5, 6]. In this method, road irregularities are described using the white noise signal based on the PSD.
Among the large number of parameters affecting the performance and design of the suspension system, identification of those with the highest influence seems vitally important. As an important part of the design optimization, sensitivity analysis is recognized as a key step for characterization of the most influential design variables [7]. Variuos methods can be found in the literature corresponding to performing sensitivity analysis.  and VERISSIMO [8] discussed the sensitivity of the ride characteristics of a road vehicle to the mechanical characteristics of the bushings used in its suspension. XU et al [9] derived sensitivity analysis formulae for optimizing vehicle suspension systems by using the pseudo excitation method (PEM). AYDIN and
and VERISSIMO [8] discussed the sensitivity of the ride characteristics of a road vehicle to the mechanical characteristics of the bushings used in its suspension. XU et al [9] derived sensitivity analysis formulae for optimizing vehicle suspension systems by using the pseudo excitation method (PEM). AYDIN and  NL
NL SOY [10] utilized design of experiments methods together with response surface methodology to determine the significant design parameters affecting impact harshness of the vehicle. In most of the methodologies presented in the literatures, the main focus has been on analytical solutions; nevertheless, in case of a complex dynamic system, derivation of the governing equations appears to be challenging. Thus, using sampling-based methods can be more effective for assessment of the complex dynamic response of a vehicle in the procedure of the suspension system optimization.
SOY [10] utilized design of experiments methods together with response surface methodology to determine the significant design parameters affecting impact harshness of the vehicle. In most of the methodologies presented in the literatures, the main focus has been on analytical solutions; nevertheless, in case of a complex dynamic system, derivation of the governing equations appears to be challenging. Thus, using sampling-based methods can be more effective for assessment of the complex dynamic response of a vehicle in the procedure of the suspension system optimization.
Design of the vehicle suspension system deals with two conflicting objectives, namely, improving vehicle handling and steering, so both should be optimized simultaneously as a multi-objective optimization of the vehicle suspension system [11-13]. Several methods have been proposed for evaluating similar multi- objective problems such as weighted factors and transformation of several objectives to a single one [14-16]. BOUAZARA [17] performed single-objective optimization of the vehicle vibration model via optimizing a single objective described by summing all the weighted factors affecting the performance of the model. In his research, the concentration was on reaching a trade-off between driving comfort as well as stability. In recent years, multi-objective algorithms have been also used in many researches [18-20]. NARIMAN- ZADEH [18] accomplished 5-objective optimization of the same vehicle model employed by BOUAZARA [17], subjected to sinusoidal double bump, using the novel optimization method of NSGA-II and reached comparatively superior results.
In most of the discussed researches, a deterministic approach has been taken toward the optimization. However, in actual engineering problems, the presence of different sources of uncertainties in model parameters, such as environmental conditions or incomplete knowledge of the problem nature cannot be ignored. It has been proved that deterministic optimum points under realistic working conditions may lead to high-risk designs instead of reliable optimum ones [21]. As a result, it is very crucial to obtain reliable and stable optimum designs by consideration of a probabilistic approach. Probabilistic optimization is based on reliable and robust design [22]. This novel type of optimization viewpoint has been observed comparatively fewer and with more limited scope of design variables in the literature. GOBBI et al [23] performed robust optimization of a two-degree-of-freedom (2 DOF) linear vehicle model considering mass of the vehicle’s body and the tire radial stiffness as stochastic design variables with Gaussian distribution. Furthermore, GATTI and PIOVAN [24] presented a preliminary study of the stochastic dynamics of the suspension system, due to the presence of uncertainties in the design parameters, in a vehicular platform modeled with a 7 degree-of-freedom ordinary differential equations system. JAMALI et al [25], used probabilistic metrics for a robust Pareto multi-objective optimum design of five-degree of freedom vehicle vibration model having parameters with probabilistic uncertainties.
In this work, both deterministic and probabilistic approaches have been utilized for multi-objective optimization of the five-degree of freedom (5 DOFs) vehicle vibration model considering random road profiles. Initially in Section 2, the deterministic optimization has been performed based on 7 design variables and 5 objective functions, and the obtained results are compared to that of Refs. [17] and [18] for the sake of verification. In this multi-objective optimization problem, criterion for the passenger’s comfort is regarded based on the standard of ISO2631 (related to whole-body exposure to vibration), and is seen as a constraint added to the problem definition. Next in Section 3, the sensitivity analysis has been performed to characterize the parameters with highest effects on the objective functions. Subsequently, the most influential parameters are characterized and considered as the variables for the probabilistic optimization. Finally in section 5, reliable and robust probabilistic optimization has been accomplished by considering the effects of uncertainties in design variables. TOPSIS method [26] for both of optimization approaches has been employed to obtain the best trade-off optimum point optimizing all objective functions simultaneously.
2 Generation of random road profiles
Road surfaces are practically defined by random functions. Moreover, if the statistical properties of the road surface derived from one particular portion of the road can be used to define the properties of the entire section of the road, then the road surface can be supposed to be a stationary stochastic process provided that the velocity of the vehicle remains constant [4].
There are different methods for obtaining the corresponding random signal in time and frequency domains [4-6]. In this research, shaping filter method has been used for generation of the random road profiles [5]. For a vehicle moving with the constant velocity of V, the road profile signal ZR(t) is obtained via the linear filter described by the following differential equation:
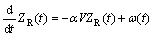 (1)
(1)
where ω(t) is the white noise function with the spectral density of ψ 2αVσ2, where σ2 indicates the variance of the road roughness, V is the vehicle velocity and a is a constant depending on the type of road surface. Based on many works in the literature, σ2=4Φ(Ω0) has been considered in this research. The reference values of PSD for Ω0=1 rad/m, Φ(Ω0), are provided based on standard of ISO8608 as given in Table 1. The differential Eq. (1) can schematically be presented in MATLAB- SIMULINK as in Fig. 1.
2αVσ2, where σ2 indicates the variance of the road roughness, V is the vehicle velocity and a is a constant depending on the type of road surface. Based on many works in the literature, σ2=4Φ(Ω0) has been considered in this research. The reference values of PSD for Ω0=1 rad/m, Φ(Ω0), are provided based on standard of ISO8608 as given in Table 1. The differential Eq. (1) can schematically be presented in MATLAB- SIMULINK as in Fig. 1.
By solving this equation, the random road profile signal in time domain (ZR(t)) is obtained as shown in Fig. 2.
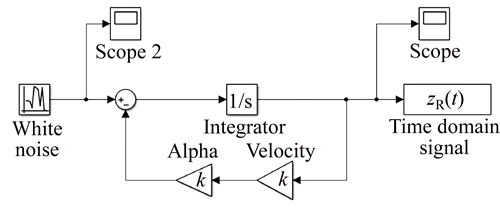
Fig. 1 Schematic view of differential Eq. (1) in MATLAB SIMULINK
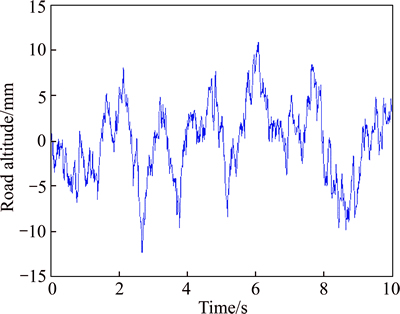
Fig. 2 Road irregularities for grade-B road profiles
For plotting the road irregularities in the frequency domain, the PSD function is also obtained. Accordingly, Fig. 3 gives the PSD for the same signal in Fig. 2, in comparison with approximations of International Organization for Standardization (ISO 8606),marked as red line.
3 Vibration model of vehicle suspension system
A five-degree of freedom (5 DOF) vehicle model is depicted in Fig. 4, where parameters ms, mc, m1, m2 and Is stand for sprung mass, seat mass, front tire mass, rear tire mass and momentum inertia of sprung mass, respectively. Additionally, Kss, Ks1, Ks2, Kp1 and Kp2 denote seat stiffness coefficient, front suspension stiffness coefficient, rear suspension stiffness coefficient, front tire stiffness coefficient, and rear tire stiffness coefficient, respectively. Css, Cs1 and Cs2 represent seat damping coefficient, damping coefficients for vehicle front and rear suspension, respectively. Lastly, l1, l2 and r provide position of the front and rear tires and seat position in relation to the center of mass, respectively. This model is basically the same model used in studies of Refs. [18] and [19]. The fixed parameters for this model are provided in Table 2.
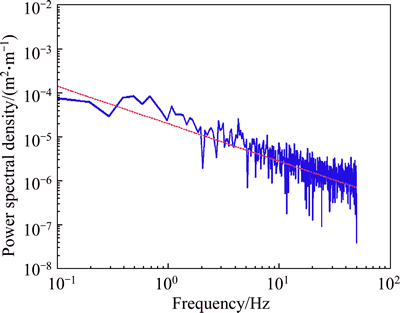
Fig. 3 PSD for a grade-B road profile (Values corresponding to ISO 8606 is shown with red line)
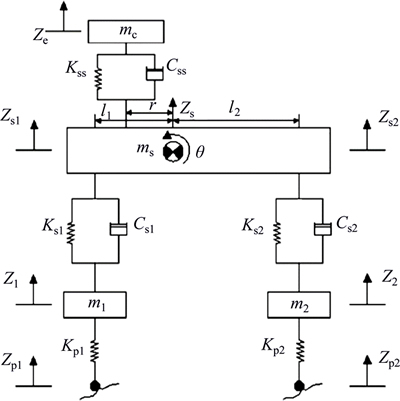
Fig. 4 Half-model of five-degree of freedom vehicle model employed in Refs. [18] and [19]
For this model, the 5 degrees of freedom include: vertical driver seat displacement (Zc), vertical displacement of the central gravity of the sprung mass (Zs), rotating motion of the sprung mass (θ), vertical displacement of the front and rear tires (Zp1 and Zp2). Additionally, the dot and double-dot symbols stand for the velocity and acceleration of the parameter,respectively.Supposing the fixed coordinate system as represented, governing dynamic equations of the system are gained. Additionally, by considering Zp1 and Zp2 as inputs and using Laplace transformation, transformation functions can be derived. When the input excitation of the system is the PSD function, the output PSD function will be as follows [27].
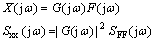 (2)
(2)
For assessment of the PSD function, one can utilize widely-used root mean square (RMS, Rms) value, and a random signal described by the PSD function can be acquired as follows [28]:
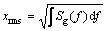 (3)
(3)
In this work, excitation function in the frequency domain for motorway road profile introduced in Ref. [17] has been obtained using shape filtering. Afterwards, dynamic response of the vertical seat acceleration at the constant vehicle velocity of 20 km/h has been calculated. RMS values for the driver seat acceleration, vertical velocity of the front and rear tires and the displacement of the front and rear tires in relation to center of the sprung mass are compared with the results of Ref. [17] in Table 3 to validate the accuracy of modeling.
Table 2 Fixed parameters for five-degree of freedom vehicle model based on Ref. [17]

4 Deterministic multi-objective optimization
In this section, optimization has been done for the 5-DOF vehicle model shown in Fig. 4. First, deterministic optimization has been established based on 7 design variables, and the results are compared to suggested optimum points of Refs. [17] and [18], where no reliability constraint has been regarded. In Ref. [17], a five-objective deterministic optimization has been done using weighted coefficients considering random road profiles. Also, in Ref. [18], deterministic optimization has been done for the same model by taking sinusoidal double bump excitation into account.
In the presented optimization process, the design variables include: Css, Cs1, Cs2, Kss, Ks1, Ks2 and r. Furthermore, the objective functions are vertical seat acceleration 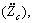 front and rear tire velocities
front and rear tire velocities 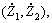 relative displacement between the sprung mass and front tire (d1) and relative displacement between the sprung mass and rear tire (d2), which characterize a criterion for the passenger’s comfort, exerted forces on the front and rear axles (stability) and working space of the front and rear suspensions, respectively. It is also assumed that the vehicle is moving at the constant speed of 20 m/s along a road with good roughness (Grade B), and its rear tire follows the same trajectory similar to the front tire with a delay of T=(I1+I2)/V. The PSD of the road is considered as shown in Fig. 3.
relative displacement between the sprung mass and front tire (d1) and relative displacement between the sprung mass and rear tire (d2), which characterize a criterion for the passenger’s comfort, exerted forces on the front and rear axles (stability) and working space of the front and rear suspensions, respectively. It is also assumed that the vehicle is moving at the constant speed of 20 m/s along a road with good roughness (Grade B), and its rear tire follows the same trajectory similar to the front tire with a delay of T=(I1+I2)/V. The PSD of the road is considered as shown in Fig. 3.
In this work, novel consideration of the passenger comfort limit is regarded based on standard of ISO2631 [29], which is added as a constraint to the optimization problem. This standard concerns exposure to whole-body vibration when working with industrial tools, in which, a method has been specified for measurement of the whole-body acceleration limit for different exposure times. Based on international standards, effects of the imposed vibration on the driver’s body is generally described considering the range of the passenger’s comfort, the working proficiency as well as health and safety considerations. The time exposure is acquired based on the mentioned criteria. The present optimization problem can be formulated as
 (4)
(4)
Table 3 Comparison of obtained results for RMS with Ref. [17]

The optimization procedure has been performed using modified NSGA-II, which has demonstrated a good capability in solving similar multi-objective optimization problems (refer to Ref. [30] for a complete description of this method). A population of 80 individuals with a crossover probability of 0.9 and mutation probability of 0.1 has been used in 500 generations. As a result, Fig. 5 represents the obtained Pareto points, which also involve the optimum points acquired in Refs. [17] and [18] for the sake of comparison and verification.
Furthermore, a comparison between values of the deterministic optimum points obtained in this research and that of Refs. [17] and [18] is provided in Table 4.
Accordingly, by considering only driver seat vertical acceleration, the obtained points show a great improvement. However, in terms of other objective functions, these points are less attractive. It must be pointed out that the optimum points in Refs. [17] and [18] violate the ISO-2631 passenger comfort constraint, as shown in Fig. 6.
This figure depicts the frequency response of driver
seat acceleration. As shown, suggested optimum points in Refs. [17] and [18] violate the comfort limits of ISO2631 within the frequency range of 5 to 9 Hz. Evidently, the obtained optimum points of this study are under the threshold of 8-hour exposure in all frequencies, and within the range of 4-8 Hz which demonstrates the highest sensitivity, their corresponding acceleration fall below 0.1 m/s2. It is worth mentioning that the driver’s vertical acceleration for the optimum point in Ref. [17] is placed below that of Ref. [18], in most of the frequencies, which emphasizes on higher reliability of the former.Nevertheless, authors in Ref. [18] demonstrated the superiority of their presented optimum point in relation to that of Ref. [17] for sinusoidal double bump excitation. In other words, for excitation type of random road profiles, the optimum point of Ref. [18] is not valid.
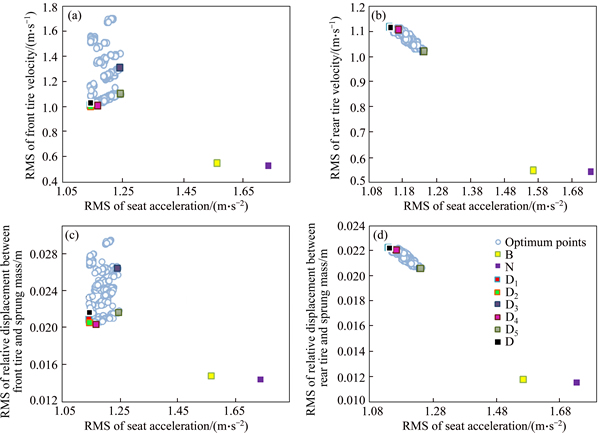
Fig. 5 Deterministic multi-objective optimization results
Table 4 A comparison between deterministic optimum points obtained in this research and in Refs. [17] and [18]
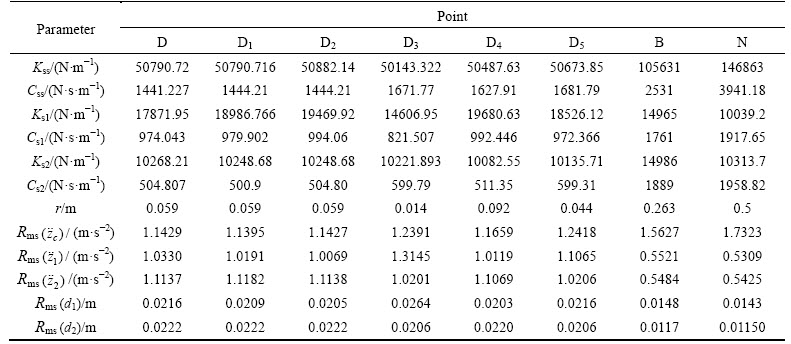
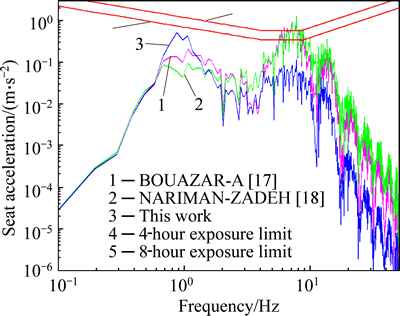
Fig. 6 Vertical seat acceleration and its limit for different frequencies based on ISO-2631
Among the non-dominant points in Fig. 5, single- objective optimum points are identified as D1 to D5, which are indicators of the minimum vertical driver’s seat acceleration, minimum vertical velocity of the front tire, minimum vertical velocity of the rear tire, minimum relative displacement of the front tire to the sprung mass and minimum relative displacement of the rear tire to the sprung mass, respectively. Within the space of optimum points given in Fig. 4, using TOPSIS method, a trade-off optimum point compromising all objective functions is introduced. This point has been marked as D in Fig. 5, which mostly lies on the border of the Pareto fronts, providing the best performance for all objective functions simultaneously.
5 Sensitivity analysis
In this section, the design variables to which the objective functions have the highest sensitivity, are achieved and regarded as uncertain parameters in the probabilistic optimization, which is performed in the next section. To this aim, sensitivity analysis of the model is performed via a sampling method based on Pearson correlation coefficient [31] as the sensitivity index. In this analysis, sensitivity of 5 objective functions introduced before are considered as the outputs of the system with respect to stiffness and damping coefficients and driver’s seat position. Obtained index for each design variable is provided in Table 5, where negative values show the inverse input-output relationship.
Furthermore, Fig. 7 shows the results of sensitivity analysis for objective functions. As shown, the vertical seat acceleration has the highest sensitivity to the damping coefficients of rear suspension, while front tire velocity and rear tire velocity are most sensitive to the front and rear damping coefficients, respectively. Notably, relative displacement of the rear and front tires to the sprung mass have the same sensitivity as the front and rear tire velocities. As a result, Cs1 and Cs2 can be concluded as the most influential parameters on the objective functions.
6 Reliability-based robust design
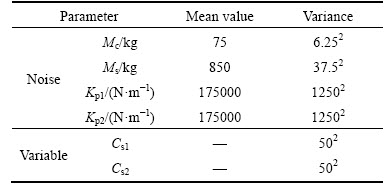
In this section, the effects of design uncertainties have been seen and a novel robust and reliable design optimization has been carried out, which to the best of our knowledge, has not previously been performed for the vehicle suspension considering random road profiles. Deterministic design variables include: Css, Kss, Ks1, Ks2 and r. While, based on the sensitivity analysis in previous section, variables Cs1 and Cs2 are supposed probabilistic. Moreover, effects of parameters such as uncertainty in driver’s weight, the sprung mass, tire stiffness under loading, vehicle velocity and so on [32], have been taken into account as the probabilistic noise parameter. Corresponding variance and mean of the probabilistic parameters are provided in Table 6.
Table 5 Values for sensitivity of objective functions to design variables based on Pearson correlation coefficient
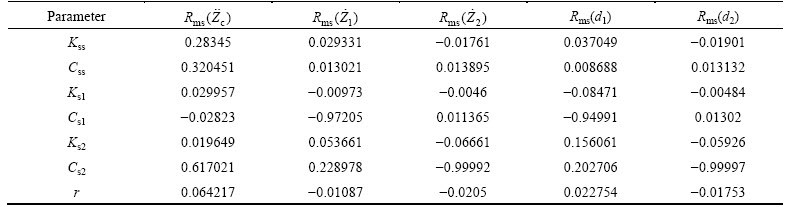
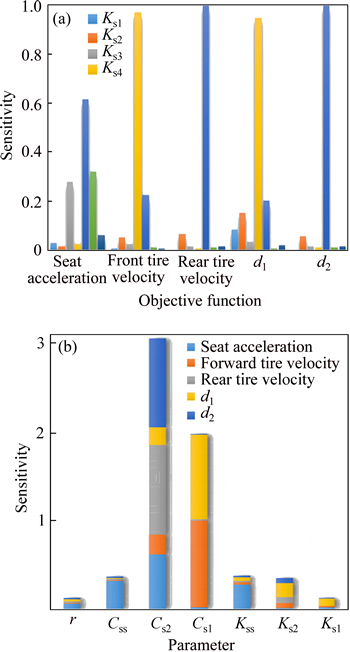
Fig. 7 Sensitivity of objective functions to design variables
In order to achieve a robust design, it is required to minimize the variance of objective functions. Also, to meet the criteria for a reliable design, the probability of violation of constraint  ISO2631 limitation, which is previously considered as a criterion for passengers’ comfort in deterministic optimization, has been accounted as the probabilistic constraint. This new probabilistic approach in the optimization problem, which comprises 10 objective functions, can be mathematically characterized as
ISO2631 limitation, which is previously considered as a criterion for passengers’ comfort in deterministic optimization, has been accounted as the probabilistic constraint. This new probabilistic approach in the optimization problem, which comprises 10 objective functions, can be mathematically characterized as
 (5)
(5)
Table 6 Mean and variance of design variables with uncertainties in probabilistic optimization
In this work, Mont Carlo method has been employed for calculation of variance and mean of the objective functions. Additionally, modified NSGA-II with the same values in the deterministic optimization has been utilized for performing the optimization process. Consequently, Figs. 8 and 9 demonstrate the obtained optimum Pareto points.
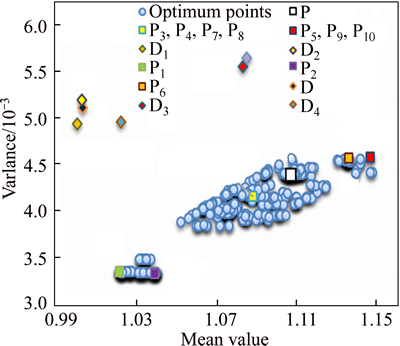
Fig. 8 Reliability-based robust multi-objective optimization results for seat acceleration
Within presented points, P1-P10 denote resulted optimum points from single-objective optimization of each objective function. Additionally, P1 and P2, P3 and P4, P5 and P6, P7 and P8 in addition to P9 and P10 are the points with the minimum variance and mean of the driver’s seat acceleration, front tire vertical velocity, rear tire vertical velocity, relative displacement of the front tire to the sprung mass, and finally, relative displacement of the rear tire to the sprung mass, respectively. Associated values of these points are tabulated in Table 7.
By compromising all objective functions simultaneously, optimum trade-off point P is achieved using TOPSIS method. Similar to deterministic optimum point in Section 3 (point D), this point also mostly lies on the borders of Pareto fronts, showing it is superior performance in view of optimizing all objective functions. Furthermore, performance of the deterministic optimum points D, D1–D10 have been evaluated in the probabilistic framework, which is evident in mentioned figures. It is worth mentioning that all objective functions have higher variance for deterministic optimum points in comparison to probabilistic ones, which particularly highlights on the hypothesis that deterministic optimum solution is high-risk and giving unstable dynamic response. The objective function values for all optimum points in this study are compared in Table 8, where the last column shows the probability of violation of passenger’s comfort constraint according to standards of ISO2631.
Evidently, this criterion for P, P1-P10 is lower than 10% as expected. However, for points D, D1, D2 and D4, it is higher than 10%, representing violation of the reliability constraint. Additionally, histogram diagrams for objective functions are shown in Fig. 10 where the vertical axis shows the frequency for 1000 data samples in optimum points.
As shown, unlike high variation of the responses for deterministic optimum points (D, D1-D5), for probabilistic ones (P, P1–P10), the responses are distributed such that the population becomes larger around the mean value, which stands for the higher robustness of the probabilistic approach in the presence of different sources of uncertainties. However, deterministic optimum points have higher variation and may lead to a high risk design.
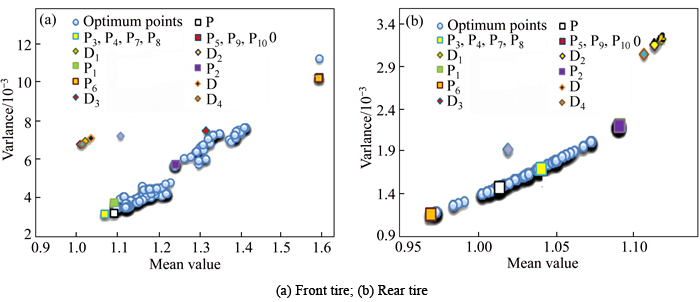
Fig. 9 Reliability-based robust multi-objective optimization results:
Table 7 Optimum points obtained from 10-objective and single-objective probabilistic optimization
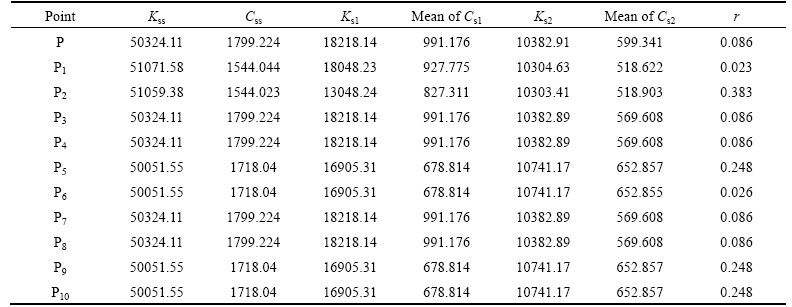
Table 8 A comparison between optimum points obtained from deterministic and probabilistic optimizations
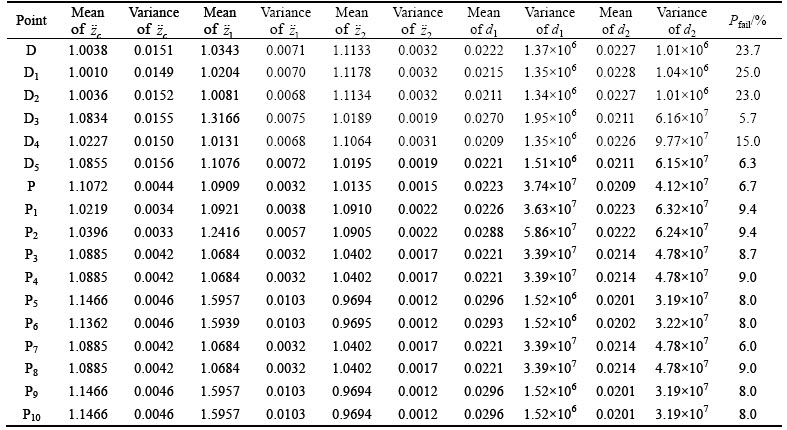
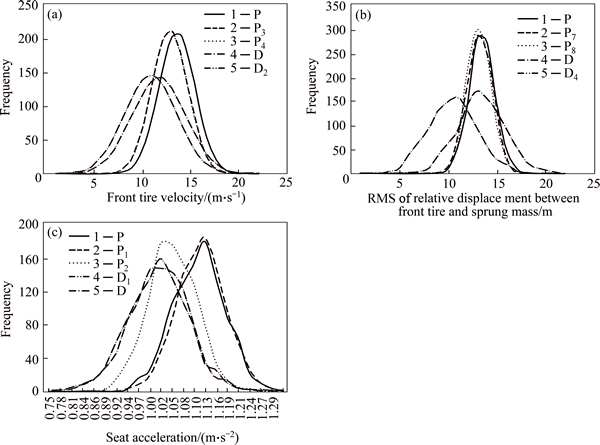
Fig. 10 Probability distribution for front tire velocity (a), front tire relative displacement (b) and driver’s seat acceleration (c)
7 Conclusions
In this research, optimization of the dynamic response of a five-degree of freedom vehicle model subjected to random road profiles, described by the PSD function, is investigated. Subsequently, a multi-objective problem consisted of 7 design variables and 5 objective functions, described in the manuscript, is defined by considering the reliability-based constraint based on the standard of ISO2631 for passenger’s comfort. Modified NSGA-II is employed for both deterministic and probabilistic optimizations. A comparison of corresponding deterministic optimum points to similar studies in the literature, demonstrates the superior performance of the present research which is accompanying with reliability metrics. Prior to probabilistic optimization, the sensitivity analysis of the vehicle model is performed. Under probabilistic conditions in the problem, it is found out that the deterministic optimum points are unreliable and high-risk points as some points violated the reliability constraint. The obtained results of this work can provide design engineers with more reliable choices.
References
[1] JAZAR R N. Vehicle dynamics: theory and application [M]. Springer Science & Business Media: 2013.
[2] DODDS C J, ROBSON J D. The description of road surface roughness [J]. Journal of Sound and Vibration, 1973, 31(2): 175-83.
[3]  J, Li Y Y, CASHELL K. The use of vehicle acceleration measurements to estimate road roughness [J]. Vehicle System Dynamics, 2008, 46(6): 483-499.
J, Li Y Y, CASHELL K. The use of vehicle acceleration measurements to estimate road roughness [J]. Vehicle System Dynamics, 2008, 46(6): 483-499.
[4] HE L, QIN G, ZHANG Y, CHEN L. Non-stationary random vibration analysis of vehicle with fractional damping [C]// Intelligent Computation Technology and Automation (ICICTA), IEEE, 2008: 150-157.
[5] TYAN F, HONG Y F, TU S H, JENG W S. Generation of random road profiles [J]. Journal of Advanced Engineering, 2009: 4(2): 1373-1378.
[6] ZHANG Y Q, ZHAO Y S, YANG J, CHEN L P. A dynamic sliding-mode controller with fuzzy adaptive tuning for an active suspension system [J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2007, 221(4): 417-428.
[7] SALTELLI A, CHAN K, SCOTT E M. Sensitivity analysis [M]. New York: Wiley, 2000.
[8]  J, VERISSIMO P. Sensitivity of a vehicle ride to the suspension bushing characteristics [J]. Journal of Mechanical Science and Technology, 2009, 23(4): 1075-1082.
J, VERISSIMO P. Sensitivity of a vehicle ride to the suspension bushing characteristics [J]. Journal of Mechanical Science and Technology, 2009, 23(4): 1075-1082.
[9] XU W T, LIN J H, ZHANG Y H, KENNEDY D, WILLIAMS F W. Pseudo-excitation-method-based sensitivity analysis and optimization for vehicle ride comfort [J]. Engineering Optimization, 2009, 41(7): 699-711.
[10] AYDIN M,  NL
NL SOY Y S. Optimization of suspension parameters to improve impact harshness of road vehicles [J]. The International Journal of Advanced Manufacturing Technology, 2012, 60(5-8): 743-754.
SOY Y S. Optimization of suspension parameters to improve impact harshness of road vehicles [J]. The International Journal of Advanced Manufacturing Technology, 2012, 60(5-8): 743-754.
[11] KARNOPP D. Analytical results for optimum actively damped suspensions under random excitation [J]. Journal of Vibration, Acoustics, Stress, and Reliability in Design, 1989, 111(3): 278-282.
[12] HAC A, YOUN I. Optimal semi-active suspension with preview based on a quarter car model [J]. Journal of Vibration and Acoustics, 1992, 114(1): 84-92.
[13] BAUMAL A E, MCPHEE J J, CALAMAI P H. Application of genetic algorithms to the design optimization of an active vehicle suspension system [J]. Computer Methods in Applied Mechanics and Engineering, 163(1): 87-94.
[14] CHI Z, HE Y, NATERER G F. Design optimization of vehicle suspensions with a quarter-vehicle model [J]. CSME Transactions, 2008, 32(2): 297-312.
[15] ALKHATIB R, JAZAR G N, GOLNARAGHI M F. Optimal design of passive linear suspension using genetic algorithm [J]. Journal of Sound and Vibration, 2004, 275(3): 665-691.
[16] SUN L, CAI X, YANG J. Genetic algorithm-based optimum vehicle suspension design using minimum dynamic pavement load as a design criterion [J]. Journal of Sound and Vibration, 2007, 301(1): 18-27.
[17] BOUAZARA M. Etude et anaslyse de la suspension active et semi-active des vehicules routters [D]. Laval: Universite Laval, 1997. (In French)
[18] NARIMAN-ZADEH N, SALEHPOUR M, JAMALI A, HAGHGOO E. Pareto optimization of a five-degree of freedom vehicle vibration model using a multi-objective uniform-diversity genetic algorithm (MUGA) [J]. Engineering Applications of Artificial Intelligence, 2010, 23(4): 543-551.
[19] GEORGIOU G, VERROS G, NATSIAVAS S. Multi-objective optimization of quarter-car models with a passive or semi-active suspension system [J]. Vehicle System Dynamics, 2007, 45(1): 77-92.
[20] CREWS J H, MATTSON M G, BUCKNER G D. Multi-objective control optimization for semi-active vehicle suspensions [J]. Journal of Sound and Vibration, 2011, 330(23): 5502-5516.
[21] KHALKHALI A, NARIMAN-ZADEH N, DARVIZEH A, MASOUMI A, NOTGHI B. Reliability-based robust multi-objective crashworthiness optimisation of S-shaped box beams with parametric uncertainties [J]. International Journal of Crashworthiness, 2010, 15(4): 443-456.
[22] PAPADRAKAKIS M, LAGAROS N D, PLEVRIS V. Structural optimization considering the probabilistic system response [J]. Theoretical and Applied Mechanics, 2004, 31(3-4): 361-394.
[23] GOBBI M, LEVI F, MASTINU G. Multi-objective stochastic optimisation of the suspension system of road vehicles [J]. Journal of Sound and Vibration, 2006, 298(4): 1055-1072.
[24] GATTI C, PIOVAN M T. Dynamic analysis of models for suspension systems of ground vehicles with uncertain parameters [C]//Congreso Argentino de  Computacional. Salta, 2012: 2745-2755.
Computacional. Salta, 2012: 2745-2755.
[25] JAMALI A, SALEHPOUR M, NARIMAN-ZADEH N. Robust Pareto active suspension design for vehicle vibration model with probabilistic uncertain parameters [J]. Multibody System Dynamics, 2013, 30(3): 265-285.
[26] SHOJAEEFARD M H, KHALKHALI A, MIANDOABCHI E. Multi-criteria decision making approach for selecting the best friction distribution in superplastic forming of a vehicle component [J]. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 2016, 230(2): 146-157.
[27] LI X R. Probability, random signals, and statistics [M]. Florida: CRC press, 1999.
[28] BRANDT A. Noise and vibration analysis: signal analysis and experimental procedures [M]. West Sussex, United Kingdom: John Wiley & Sons, 2011.
[29] CAO J T, LI P, LIU H. An interval fuzzy controller for vehicle active suspension systems [J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(4): 885-895.
[30] DEB K, PRATAP A, AGARWAL S, MEYARIVAN T A. A fast and elitist multiobjective genetic algorithm: NSGA-II [J]. Evolutionary Computation, IEEE Transactions on, 2002, 6(2): 182-197.
[31] HAMBY D M. A review of techniques for parameter sensitivity analysis of environmental models [J]. Environmental Monitoring and Assessment, 1994, 32(2): 135-154.
[32] SMITH N D. Understanding parameters influencing tire modeling. Formula SAE Platform [D]. Colorado, United States: Colorado State University, 2004.
(Edited by FANG Jing-hua)
Cite this article as: Abolfazl Khalkhali, Morteza Sarmadi,Sina Yousefi. Reliability-based robust multi-objective optimization of a 5-DOF vehicle vibration model subjected to random road profiles [J]. Journal of Central South University, 2017, 24(1): 104-113. DOI: 10.1007/s11771-017-3413-0.
Received date: 2015-12-02; Accepted date: 2016-04-11
Corresponding author: Morteza Sarmadi, Research Engineer; Tel: +98-2177491225; E-mail: mortezasarmady@alumni.iust.ac.ir