Trans. Nonferrous Met. Soc. China 24(2014) 1951-1958

Stability of remelting and solidification interfaces of triple-phase region during peritectic reaction at lower speed

Shu-jie WANG^1,2, Liang WANG¹, Liang-shun LUO¹, Yan-qing SU¹, Fu-yu DONG¹, Jing-jie GUO¹, Heng-zhi FU¹

1. School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China;

2. Science and Technology on ASIC Laboratory, Hebei Semiconductor Research Institute, Shijiazhuang 050051, China

Received 25 March 2013; accepted 16 March 2014

Abstract: Peritectic reaction was studied by directional solidification of Cu-Ge alloys. A larger triple junction region of peritectic reaction was used to analyze the interface stability of the triple junction region during peritectic reaction. Under different growth conditions and compositions, different growth morphologies of triple junction region are presented. For the hypoperitectic Cu-13.5%Ge alloy, as the pulling velocity (v) increases from 2 to 5 μm/s, the morphological instability of the peritectic phase occurs during the peritectic reaction and the remelting interface of the primary phase is relatively stable. However, for the hyperperitectic Cu-15.6%Ge alloy with v=5 μm/s, the nonplanar remelting interface near the trijunction is presented. The morphological stabilities of the solidifying peritectic phase and the remelting primary phase are analyzed in terms of the constitutional undercooling criterion.

Key words: peritectic reaction; Cu-Ge alloys; directional solidification; microstructure; constitutional undercooling

1 Introduction

Peritectic reaction can be found in many materials, such as Fe- and Cu-alloys, YBa₂Cu₃O_y superconductors and Nd–Fe–B magnetic materials [1-7]. It involves one solid phase reaction with a liquid phase on cooling to produce a second solid phase [1]. The morphology and volume fraction of peritectic two phases will directly influence mechanical and physical properties of the materials. Many studies on peritectic solidification have focused on the microstructure and phase selections, peritectic transformation kinetics, and formation of banded structure [1]. However, there is limited understanding of the process of peritectic reaction during directional solidification. And very little is known about the morphological stability of the two phases of the trijunction region during peritectic reaction.

FREDRIKSSON and [8] studied the solidification mechanism of peritectic Cu-Sn and Al-Mn alloys. KERR and KURZ [1] reviewed various peritectic systems comprehensively. HILLERT [9] predicted the shape of triple junction region. SHA et al [10] proposed more detailed theory on peritectic reaction process. Peritectic reaction is characterized by the motion of triple phase junction of peritectic reaction. Solidification of the peritectic phase, remelting and resolidification of the primary phase will occur in the vicinity of the triple phase junction during peritectic reaction [1]. The missing part of the primary α-phase ahead of the triple phase junction proves the occurrence of the remelting of α-phase. The remelting interface does not contact with the triple phase junction [10-14]. Under the condition of the balance of surface tension, the re-solidification of α-phase forms near the triple phase junction, which contacts with the triple phase junction [9]. Although the phenomena have been presented, the solidifying peritectic phase and the remelting primary phase usually grow with a planar front because the acquired triple phase regions are very small [8-14]. By now, the morphological instabilities of the solidification and remelting phases near triple phase junction have not been observed. The models on the peritectic reactions do not consider the question of the interface stability of the phases.

In order to create a larger triple phase region to study the interface stability of the phases, systematic experiments were carried out in Cu-Ge peritectic system (see Fig. 1) [3]. Two features make the system rather unique for the observation of the triple phase region of the peritectic reaction. Firstly, the big density difference between the constituents (ρ_Cu>ρ_Ge) leads to the solute convection, which induces lateral macrosegregation of Ge and macroseparation of the two phases. Secondly, the big difference of concentration between the primary and the liquid phases induces a very big freezing range (120 K for hypoperitectic alloys) such that peritectic reaction in this system is easily observable. This is likely the principal reason why it looks so long to find clear experimental evidences of the stabilities of remelting and solidification interfaces of triple phase region during peritectic reaction.

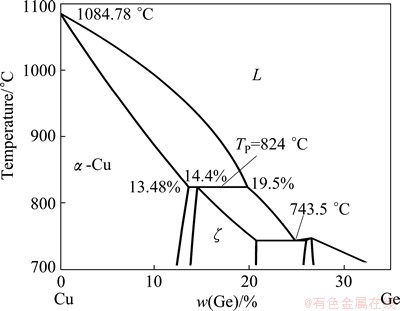
Fig. 1 Phase diagram of peritectic Cu-Ge system [3]

The main purpose of this work is to investigate the morphological stabilities of peritectic two phases during peritectic reaction. To reveal the morphological characteristics of the triple phase region, a macroseparation structure of the two phases is used to magnify the triple phase region. The different growth morphologies of the two phases at the triple phase region of peritectic reaction are observed in the macroseparation structure. The constitutional undercooling criterion is used to analyze the morphological stabilities of the solidifying peritectic phase and the remelting of the primary phase during peritectic reaction.

2 Experimental

Four master alloys with nominal compositions of 13.5%, 14.5%, 15.5% and 16.5% Ge were prepared from 99.99% purity copper and 99.99% purity germanium. The peritectic reaction α(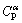=13.48% Ge) + L(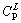= 19.5% Ge) →ζ(=14.4% Ge) occurs at 824 °C. The phase diagram for Cu-Ge system is shown in Fig. 1 [3]. The samples were solidified in an improved Bridgman-type furnace, which consisted of two heaters: primary heater I and secondary heater II (W tubes heated by resistance heating). The temperature gradient of the Cu-Ge sample can be regulated by changing the temperatures of the two heaters. The Cu-Ge samples were quenched in liquid metal cooling bath. Electrolytic deep etching technique was applied to differentiating the quenched solid/liquid boundaries. The electrolytic etching was performed at 293 K for 60 s in a solution consisting of 30% H₂O and 70% H₃PO₄ (by volume). Microstructural observation of the quenched interface was made using an Olympus optical microscope. Steady-state temperature profiles during solidification were measured using a PtRh30- PtRh6 thermocouple inserted down the center of the samples.

3 Results and discussion

3.1 Microstructure

Figures 2(a) and (b) show the longitudinal microstructures of the directionally solidified Cu-15.5% Ge alloys at G=25 K/mm. At v=15 μm/s, the dendritic α phase solidifies in front of the dendritic ζ phase, as shown in Fig. 2(a). As the velocity decreases to 3 μm/s, the α phase changes from dendritic to cellular, and the ζ phase changes from dendritic to near planar (Fig. 2(b)). In the present work, the composite structure consisting of both α and ζ in the whole is called conventional structure, as shown in Figs. 2(a) and (b). Figures 2(c) and (d) show the longitudinal microstructures of the directionally solidified Cu-13.5% Ge alloys at G=25 K/mm. At v=15 μm/s, the conventional structure of the dendritic α and ζ is obtained again (Fig. 2(c)). As the velocity decreases to 3 μm/s, a radial macroseparation structure of the two phases forms, as shown in Fig. 2(d). The structure that the primary α-phase locates in the center and is surrounded by the peritectic ζ-phase in the whole is called macroseparation structure (see Fig. 2(d)), which is used to analyze the interface stability of the triple phase region during the peritectic reaction.

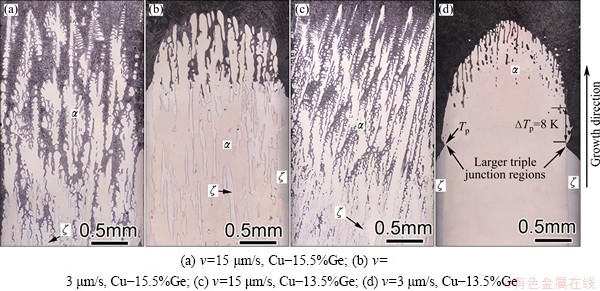
Fig. 2 Microstructures of longitudinal sections around solidification interface at G=25 K/mm

Fig. 3 Schematic illustration of peritectic phase diagram (a) and formation (b) of macroseparation structure

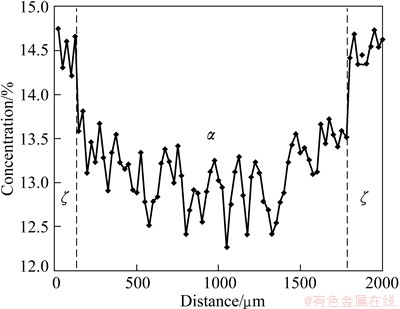
Fig. 4 Composition profile in a macroseparation structure

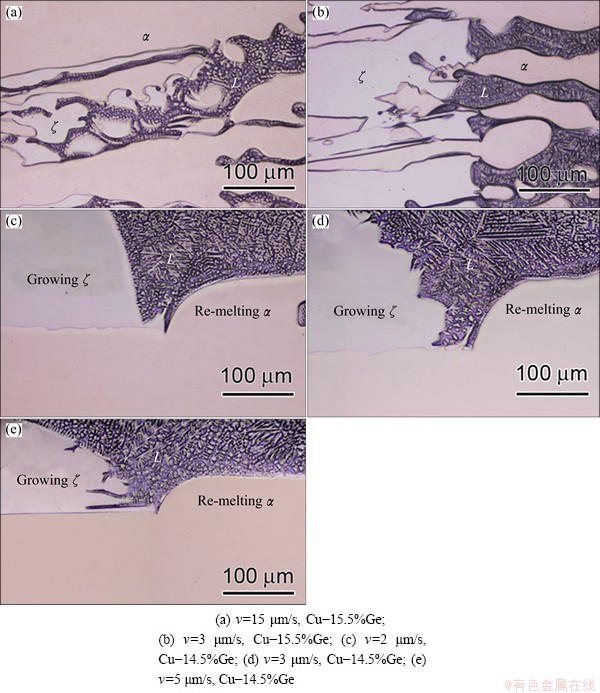
Fig. 5 Microstructures of triple junction regions at G=25 K/mm

The macroseparation structure is mainly induced by the double-diffusive convection and the lateral temperature gradient. As the rejected Ge atoms are lighter than the Cu atoms, double diffusive convection forms at lower velocities [15]. Figure 3 shows the formation of macroseparation structure. The fluid flow directly pushes the Ge atoms from the center to the border of the crucible, which induces a lateral concentration gradient and a convex solid/liquid interface (Fig. 3(b)). Figure 4 shows the macrosegration of Ge in the macroseparation structure. When the dendrite spacing is smaller, the lateral concentration gradient along solid-liquid front will lead to peritectic two phases separately growing along radial direction, as shown in Fig. 2(d). In the macroseparation structure, a lager triple junction region forms near the peritectic temperature T_P (see Fig. 2(d)). At T_P, the peritectic ζ phase grows along the solid/liquid (S/L) interface. Solute rejected by the ζ phase diffuses through the liquid to the α phase contributing to its remelting. In Fig. 2(d), the solidification interval of the remelting region (△T₀) is about 8 K, which is smaller than the whole solidification interval of the solidification region.

3.2 Morphological evolution of triple junction region

The conventional morphologies of the peritectic reaction regions is shown in Figs. 5(a) and (b), which are obtained in conventional structure. The peritectic reaction regions are so small that many morphological characteristics of the triple phase regions cannot be observed very distinctly after quenching. And the bumpy surface and solute enrichment among secondary dendrite arms also influence the observation of the morphologies of triple junction region.

However, in the macroseparation structure of the two phases, a larger triple phase region forms, as marked by the green arrows in Fig. 2(d). Figures 5(c-e) show the morphologies of the larger triple phase regions under different growth conditions. Accompanying the growth of the peritectic phase, the remelting phenomena of the primary α phase are clearly presented. At v=2 μm/s, the planar ζ phase grows along the α phase accompanied by remelting of the α phase, as shown in Fig. 5(c). The remelting interface exhibits a smooth parabolic shape. As the velocity increases to 5 μm/s, the ζ phase changes from planar to dendritic (see Figs. 5(c-e)). Figure 6 shows the changes in interface morphology with growth velocity for the Cu-16.5%Ge alloy. At v=2 μm/s, the ζ phase still exhibits planar morphology (Fig. 6(a)). However, when the velocity reaches 5 μm/s, the ζ phase exhibits cellular or dendritic morphology and the nonplanar remelting interface near the trijunction is presented, as shown in Fig. 6(b). In Fig. 6, the thickness of the growing ζ phase and the remelting α phase significantly increases because of the increase of alloy composition. In addition, Figs. 5 and 6 show that the temperature difference of the ζ interface is below about 1 K than that of the trijunction.

4 Interface stability analysis of triple junction region

Under different growth conditions, the growing ζ and remelting α phases exhibit different growth morphologies during migration of the triple junction regions. The most obvious characteristics in the morphologies of triple junction region are the formation of nonplanar α and ζ.

4.1 Interface stability of growing ζ phase

Under high pulling velocities, the instability of the growing (solidifying) ζ interface can be explained by constitutional undercooling theory. The driving force for the growth of solidification perturbations is expressed as:

                              (1)

where 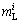 is the liquidus slope of the i phase and G_c is the concentration gradient in liquid at the phase interface.

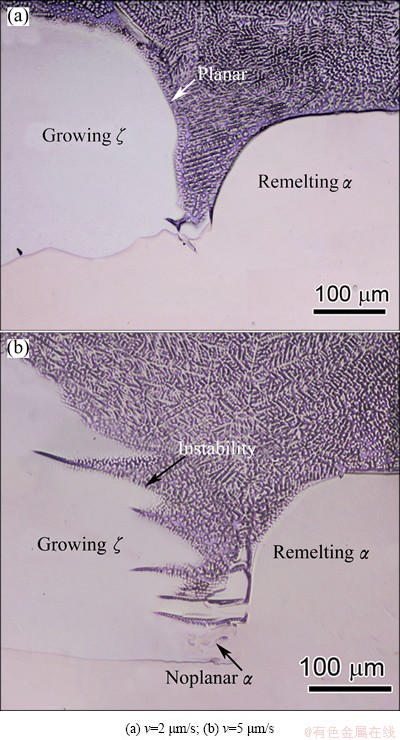
Fig. 6 Morphologies of triple junction region for Cu-16.5%Ge alloys at G=25 K/mm

This equation can be conceived to represent the degree of constitutional undercooling.

Figure 7 shows the simplified schematic of the growing ζ and the remelting α, which gives the conditions leading to the instabilities of the growing ζ interface. The liquid phase contacting with the growing ζ phase is rich in solute Ge at 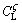 (Figs. 7(a-b)). As the ζ phase grows, the peritectic ζ phase rejects solute to the α interface and a solute boundary layer is built up from the ζ interface to the remelting α interface, as shown in Fig. 7(a). The equilibrium liquidus temperature of the ζ and α phases (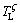and 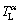, see Fig. 7(c)) is given by the phase diagram (see Fig. 7(b)). A perturbation at the growing ζ/liquid interface will grow into the liquid if _m is negative (see Fig. 7(c), ).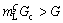

Neglecting solid-state diffusion, the use of Fick’s first law of diffusion and the application of a mass balance of the solidifying ζ interface result in the following differential equation:

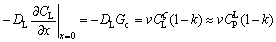  (2)

Combining Eq. (1) and Eq. (2),

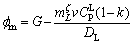                      (3)

where D_L is the solute diffusion coefficient in the liquid; k is the partition coefficient (k=0.74); 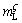 is the liquidus slope of ζ.

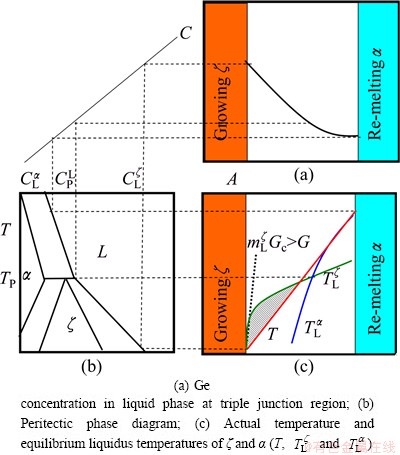
Fig. 7 Schematic illustration of instabilities of solidification interface at triple junction region of peritectic reaction

When v=2 μm/s and G=25 K/mm, taking 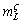=10 K/%Ge (measured using the phase diagram) and D_L=5×10^-9 m²/s (determined by the plane front growth limit), the _m value is estimated as

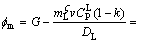
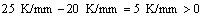
When v=5 μm/s and G=25 K/mm, the _m value is estimated as

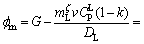
Similar to directional solidification of single phase alloy, the morphological instability occurs under high growth velocities during the migration of the triple phase region. However, the morphological stability of ζ is irrelevant to initial alloy composition, as shown in Eq. (3). This is because during peritectic reaction, the ζ phase of concentration  will directly form at T_P within the peritectic composition range of 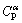-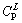. Only the volume fraction of ζ is relevant to initial alloy composition.

4.2 Interface stability analysis of remelting α phase

4.2.1 Constitutional undercooling in remelting phase

Similar to the analysis of constitutional undercooling theory, a solid region of constitutional superheating is presented ahead of the remelting interface when the melting velocity v is greater than a critical value v_CS

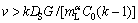                       (4)

where k is the solute segregation coefficient, D_S is the solute diffusion coefficient in the solid, and 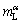 is the liquidus slope of α. The melting process occurs at a negative temperature gradient (from high temperature to low temperature). In general, the solid solute diffusion coefficient at melting point ranges from 10^-14 to 10^-12 m²/s, which is far less than the liquid solute diffusion coefficient (about 5×9 m²/s). Thus, the constitutional superheating theory predicts that a melting interface would be less stable than the solidifying interface. In addition, according to the stability theory of melting interface [16,17], the critical value v_CS is only 0.2-0.5 μm/s for G=25 K/mm and v=5 μm/s.

However, Fig. 5(e) shows that the remelting interface is more stable under high pulling velocity. Different from the remelting process, the remelting of the primary phase during peritectic reaction occurs at a positive temperature gradient (from low temperature to high temperature). Figure 8 shows that the constitutional undercooling forms in the remelting solid-α front during peritectic reaction. The α phase of concentration  firstly solidifies at higher temperature 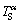 (point B, Fig. 8(a)). And the remelting of the α phase occurs at lower temperature  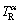(point A, Fig. 8(a)). However, at 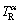, the equilibrium composition of the remelting α interface  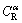is higher than . Thus, during steady state peritectic reaction, solute diffusion from the liquid phase to the α phase occurs at the remelting interface and a concentration gradient is established in the solid (see Fig. 8(b)). The α-solidus temperature corresponding to the concentration field () and the local temperature (T) in the solid is shown in Fig. 8(c). The α phase ahead of the remelting interface is constitutionally undercooled with respect to the α-solidus.

Fig. 8 Formation of constitutional undercooling in remelting solid-α phase during peritectic reaction

The solute distribution in the boundary layer in the state region is given by the differential equation:

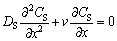                         (5)

The boundary conditions for the initial transient are 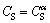 for  (The thickness of the A-B cross section (Fig. 8(a)) and 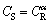 for 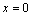. The solute distribution is obtained

          (6)

The concentration gradient at the remelting interface (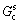) is given by

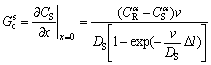          (7)

The 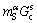 can be calculated from

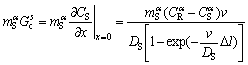      (8)

The value of 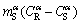 is equal to the temperature interval ,

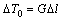                    (9)

Combining Eq. (1), Eq. (8) and Eq. (9),

      (10)

Due to 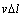/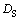>0 and G>0, _m is always less than zero (_m<0). Thus, the constitutional undercooling in the remelting phase is always presented during the migration of the triple phase region. The constitutional undercooling improves the stability of the remelting interface. Based on the above analysis, the remelting interface is more stable because of the constitutional undercooling in solid phase.

In addition, linear stability analysis [16,17] pointed out that solute diffusion in the liquid phase also has a drastic stabilizing effect on the remelting interface. JABBAREH and ASSADI [18] found that low temperature gradient (G) and high cooling rate of the remelting interface (Gv) will lead to the morphological instability of the remelting interface. The morphological instability of the remelting interface can occur at high pulling velocities. Deeper analysis and systematic experimentation will further explain the morphological stability of the remelting interface under different growth velocities.

4.2.2 Formation of nonplanar remelting α interface

However, for the Cu-16.5%Ge alloy and v=5 μm/s, the nonplanar remelting interface of α near the trijunction is presented, as shown in Fig. 6(b). The remelting process is directly related to the solute diffusion of the trijunction region. Because the equilibrium composition of the ζ phase is higher than that of the α phase (14.4 and 13.48), the growth of ζ will consume more solute that cannot be compensated by the remelting of α. In other words, the migration of the triple phase region will decrease the liquid composition of the triple phase region. Thus, the lateral diffusion of Ge from the interface of ζ  to the trijunction region compensates the loss of Ge, as shown in Fig. 9(a). Lower pulling velocities ensure that there is sufficient time to contribute to the lateral diffusion of Ge and keep the stable migration of the trijunction region. When the pulling velocity is higher, the compensation of Ge cannot be prompted, which decreases the liquid concentration of the cellular-ζ and increases the tip temperature of the cellular-ζ. Thus, when the pulling velocity is higher, the tip of the cellular-ζ can contact with the remelting interface (e.g. points C and D in Fig. 8(b)). As the peritectic reaction progresses, the remelting cannot occur at the contact areas. Then the part of the α phase behind the points C and D is wrapped in the ζ phase (see Figs. 9(c) and (d)). In the case, the remelting process is unstable.

Thus, when the thickness of the remelting phase (η) is much smaller than the diffusion length (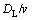), the remelting region is stable.

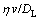<<1                                (11)

Namely, when the remelting phase is thicker and the pulling velocity is higher, nonplanar remelting α interface can form in the vicinity of the trijunction. In Fig. 5(c), the thickness of the remelting phase (η) is about 0.5×10^-4 m and the pulling velocity (v) is 5×10^-6 m²/s. Then ηv/D_L is in the order of 10^-2-10^-3, much smaller than 1. In the case, the remelting α interface is smooth. In Fig. 6(b), η is about 2.5×10^-4 m and v is 5×10^-6 m²/s. Then ηv/D_L is about 0.3. In the case, because the Ge atoms near the trijunction cannot be compensated timely, the tip of the cellular-ζ can contact with the remelting interface. Thus, the remelting α front is nonplanar.

Fig. 9 Morphological schematic of triple phase region during peritectic reaction and diffusion of Cu and Ge atoms

5 Conclusions

1) A large triple junction region of peritectic reaction is obtained in directionally solidified Cu-Ge alloys. Under higher pulling velocity, the morphological instability of the peritectic phase forms during the peritectic reaction, but the remelting interface of the primary phase is relatively stable.

2) The formation of the interface instability of the peritectic phase is because the liquid at and ahead of the solidifying interface is constitutionally undercooled with respect to the peritectic phase. Because the liquid composition of the triple junction is almost constant during the peritectic reaction, the morphological stability of ζ is irrelevant to initial alloy composition, which is mainly dependent on the growth conditions.

3) Constitutionally undercooling in the solid primary phase improves the interface stability of the remelting primary phase. When the remelting phase is thicker and the pulling velocity is higher, the loss of Ge at the trijunction region cannot be timely compensated and nonplanar remelting α interface can form in the vicinity of the trijunction.

References

[1] KERR H W, KURZ W. Solidification of peritectic alloys [J]. International Materials Reviews, 1996, 41(4): 129-164.

[2] HU Xiao-wu, LI Shuang-ming, GAO Si-feng, LIU Lin, FU Heng-zhi. Effect of melt convection on primary dendrite arm spacing in directionally solidified Pb-26%Bi hypo-peritectic alloys [J]. Transactions of Nonferrous Metals Society of China, 2011, 21: 65-71.

[3] ZHAI W, GENG D L, WANG W L, WEI B. A calorimetric study of thermodynamic properties for binary Cu-Ge alloys [J]. Journal of Alloys and Compounds, 2012, 535: 70-77.

[4] YANG Jie-ren, CHEN Rui-run, DING Hong-sheng, SU Yan-qing, HUANG Feng, GUO Jing-jie, FU Heng-zhi. Numerical calculation of flow field inside TiAl melt during rectangular cold crucible directional solidification [J]. Transactions of Nonferrous Metals Society of China, 2012, 22: 157-163.

[5] ZHONG Hong, LI Shuang-ming, Hai-yan, LIU Lin, ZOU Guang-rong, FU Heng-zhi. Microstructure evolution of peritectic Nd₁₄Fe₇₉B₇ alloy during directional solidification [J]. Journal of Crystal Growth, 2008, 310(14): 3366-3371.

[6] HU X W, LI S M, GAO S F, LIU L, FU H Z. Peritectic transformation and primary α-dendrite dissolution in directionally solidified Pb-26%Bi alloy [J]. Journal of Alloys and Compounds, 2010, 501: 110-114.

[7] SUMIDA M. Evolution of two phase microstructure in peritectic Fe-Ni alloy [J]. Journal of Alloys and Compounds, 2003, 349: 302-310.

[8] FREDRIKSSON H, T. Mechanism of peritectic reaction and transformations [J]. Material Science, 1982, 16: 283-294.

[9] HILLERT M. Solidification and casting of matals [M]. London: The Metall Society, 1979: 81-87.

[10] SHA G, O’REILLY K A Q, CANTOR B, TITCHMARSHA J M, HAMERTON R G. Quasi-peritectic solidification reactions in 6xxx series wrought Al alloys [J]. Acta Materialia, 2003, 51: 1883-1897.

[11] PHELAN D, REID M, DIPPENAAR R. Kinetics of peritectic reaction and transformation in Fe-C alloys [J]. Materials Science and Engineering A, 2008, 477: 226-232.

[12] SHIBATA H, ARAI Y, SUZUKI M, EMI T. Kinetics of peritectic reaction and transformation in Fe-C [J]. Metallurgical and Material Transaction B, 2000, 31: 981-991.

[13] McDONALD N J, SRIDHAR S. Peritectic reaction and solidification in iron-nickel alloys [J]. Metallurgical and Material Transaction A, 2003, 34: 1931-1940.

[14] StJOHN D H. The peritectic reaction [J]. Acta Metallurgica Materialia, 1990, 38: 631-636.

[15] DREVET B, NGUYEN THI H, CAMEL D, BILLIA B, DUPOUY M D. Solidification of aluminium-lithium alloys near the cell/dendrite transition-influence of solutal convection [J]. Journal of Crystal Growth, 2000, 218: 419-443.

[16] CHEN H S, JACKSON K A. Stability of a melting interface [J]. Journal of Crystal Growth, 1971, 8: 184-190.

[17] BENIELLI D, BERGEON N, JAMGOTCHIAN H, BILLIA B, VOGEV P H. Free growth and instability morphologies in directional melting of alloys [J]. Physical Review E, 2002, 65(5): 051604.

[18] JABBAREH M A, ASSADI H. Modelling of microstructure evolution in transient-liquid-phase diffusion bonding under temperature gradient [J]. Scripta Mater, 2009, 60: 780-782.

低速包晶反应三相区重熔与凝固界面的稳定性

王书杰^1,2，王 亮¹，骆良顺¹，苏彦庆¹，董福宇¹，郭景杰¹，傅恒志¹

1. 哈尔滨工业大学 材料科学与工程学院，哈尔滨 150001；

2. 中国电子科技集团公司第十三研究所 专用集成电路国防科技重点实验室，石家庄 050051

摘  要：通过定向凝固实验，研究Cu-Ge合金中的包晶反应过程。大的包晶反应三相区被用于研究包晶反应期间三相区界面的稳定性。在不同的生长条件和成分下，三相区呈现不同的生长形态。在 Cu-13.5%Ge亚包晶合金中，随着抽拉速率从 2 μm/s 提高到 5 μm/s，观察到了包晶相界面的失稳现象，而此时初生相的熔化界面相对稳定。但在 Cu-15.6%Ge 过包晶合金中，当抽拉速率达到5 μm/s时，初生相重熔界面呈现非平面形态。基于成分过冷理论，分析初生相重熔界面和包晶相凝固界面的形态稳定性。

关键词：包晶反应；Cu-Ge 合金；定向凝固；组织；成分过冷

(Edited by Hua YANG)

Foundation item: Projects (50901025, 50975060, 51331005) supported by the National Natural Science Foundation of China; Project (2011CB610406) supported by the National Basic Research Program of China; Projects (201104420, 20090450840) supported by China Postdoctoral Science Foundation; Project (JC201209) supported by Outstanding Young Scientist Foundation of Heilongjiang Province, China; Project (HIT.BRET1.20100008) supported by the Fundamental Research Funds for Central Universities, China

Corresponding author: Yan-qing SU; Tel/Fax: +86-451-86417395; E-mail: suyq@hit.edu.cn

DOI: 10.1016/S1003-6326(14)63276-3