J. Cent. South Univ. (2017) 24: 2342-2352

DOI: https://doi.org/10.1007/s11771-017-3646-y

Blind adaptive constrained constant modulus algorithms based on unscented Kalman filter for beamforming

QIAN Hua-ming(钱华明)¹, LIU Ke(刘可)¹, JIAO Zhi-bo(焦志博)², MA Jun-da(马俊达)¹

1. College of Automation, Harbin Engineering University, Harbin 150001, China;

2. Hainengda Communication Co., Ltd., Shenzhen 518000, China

Central South University Press and Springer-Verlag GmbH Germany 2017

Abstract: This work proposes constrained constant modulus unscented Kalman filter (CCM-UKF) algorithm and its low-complexity version called reduced-rank constrained constant modulus unscented Kalman filter (RR-CCM-UKF) algorithm for blind adaptive beamforming. In the generalized sidelobe canceller (GSC) structure, the proposed algorithms are devised according to the CCM criterion. Firstly, the cost function of the constrained optimization problem is transformed to suit the Kalman filter-style state space model. Then, the optimum weight vector of the beamformer can be estimated by using the recursive formulas of UKF. In addition, the a priori parameters of UKF (system and measurement noises) are processed adaptively in the implementation. Simulation results demonstrate that the proposed algorithms outperform the existing methods in terms of convergence speeds, output signal-to- interference-plus-noise ratios (SINRs), mean-square deviations (MSDs) and robustness against steering mismatch.

Key words: constrained constant modulus criterion; blind beamforming; unscented Kalman filter; generalized sidelobe canceller

1 Introduction

The problem of extracting signal of interest (SOI) and suppressing interference signals is a hot topic in array signal processing area. To address this problem, adaptive beamforming algorithms, enabling an antenna array to form high-gain beam towards a given direction of interest and direct nulls in the directions of arrival (DOAs) of the interference signals, are widely used in various applications [1–6], such as radar, sonar, wireless communication and medical ultrasound imaging. Unlike adaptive beamforming algorithms, blind adaptive beamforming algorithms save a large amount of the available spectrum and have attracted considerable attentions due to no need of a known reference sequence.

In the existing blind adaptive beamforming algorithms, the linearly constrained blind adaptive beamforming algorithms [7–18] have received a great interest in the recent twenty years. In general, the linear constraints correspond to the prior knowledge of the DOA of the SOI. The most promising linearly constrained blind adaptive beamforming algorithms can be mainly divided into the following two categories: the constrained minimum variance (CMV) criterion-based algorithms and the constrained constant modulus (CCM) criterion-based algorithms. The cost function of the CMV-based algorithms can obtain the optimum weight vector of the beamformer by minimizing the output power while maintaining the array response in the direction of the SOI to be a constant. Whereas, the CCM-based algorithms design the cost function in such a way that they penalize the deviation of the squared output from the constant modulus value of the SOI and make the weight vector satisfy certain linear constraints.Some literatures [8–12] indicate that the CCM-based algorithms are superior to the CMV-based algorithms in terms of convergence speeds, output SINRs and robustness against steering errors. Therefore, the proposed algorithms adopt CCM criterion.

In order to obtain low computational complexities, some adaptive-implementation algorithms, such as the stochastic gradient (SG) algorithm and the recursive least squares (RLS) algorithm, are combined with the CMV and CCM criterions for blind beamforming. The SG [19, 20] is a simple and low-complexity algorithm but suffers from slow convergence. Unlike the SG algorithm, the convergence speed of the RLS algorithm [21] is independent of the eigenvalue spread of the covariance matrix of the received data. Thus, the RLS algorithm owns faster convergence speed but requires higher computational load than the SG algorithm. However,there also exists a noticeable problem of how to set the iteration parameters of algorithms, such as the step size of the SG and the forgetting factor of the RLS. Inappropriate parameters chosen for the SG and RLS algorithms can result in performance degradation or even system instability.

Recently, BHOTTO and BAJIC [22], without incorporating the above linearly constrained optimization criterions, apply UKF to the blind beamforming and demonstrate the superiority over the RLS and SG algorithms in both convergence speed and output SINR. However, UKF has higher computational cost than the SG and RLS algorithm. Due to the above facts, it motivates us to combine UKF with the CCM criterion to propose a new blind adaptive algorithm called CCM- UKF for blind adaptive beamforming. Furthermore, to reduce computational cost and enhance convergence speed, the lower-complexity version of CCM-UKF called RR-CCM-UKF is also developed by using the reduced-rank technique.

In this work, the CCM-UKF and RR- CCM-UKF algorithms are devised according to the CCM criterion and operate in the GSC structure. The CCM-based cost function is changed to be a state space model so as to obtain the optimum weight vector of the beamformer by using UKF. In order to be applied readily, the system noise and measure noise in the proposed algorithms can be calculated adaptively in the implementation. Simulation results indicate that the proposed algorithms have performance improvement in terms of convergence speeds, output SINRs and robustness compared with the CCM-RLS and CMV-RLS algorithms [8, 12]. Especially, with a large number of sensors, the RR-CCM-UKF algorithm just needs lower computational cost than the RLS-type algorithms.

Notation: Upper and lower bold face letters denote matrices and column vectors, respectively. Superscripts (·)^T, (·)^H, (·)^* and (·)^–1 denote transpose, conjugate- transpose, complex conjugate and inverse, respectively. E{·} denotes expectation operation. 1_L×G and 0_L×G present all-ones and all-zeros vector, respectively, where L and G are the number of dimensions. I_L is a L×L -dimensional unit matrix.

2 System model and problem formulation

Let us consider a uniform linear array (ULA) composed of M identical omnidirectional antenna elements. There are q narrowband signals from far field to impinge on the ULA. The received vector 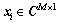[23] can be modeled as

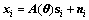                              (1)

where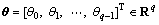presents the vector composed of the signal DOAs,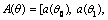 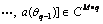presents the signal steering matrix, the normalized steering vector 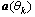can be obtained as

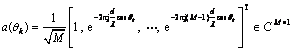(2)

and d=λ/2 presents the inter-element space, λ presents the wavelength, s_i presents the input signal vector, 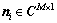presents the sensors noise vector, which is assumed to be a Gaussian white noise vector, i is the snapshot number.

The beamformer based on the GSC structure [24] shown in Fig. 1, in which a main branch operates in parallel with an auxiliary branch, is focused in this work. The main branch contains the components composed of the SOI, inference signals and noise signals while the auxiliary branch cancels the SOI component by using the signal blocking matrix B. Therefore, the difference between the output of the main branch and auxiliary branch can be used to estimate the SOI. 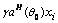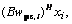In general, the outputs of the main branch and the auxiliary branch are and respectively. Thus, the output of the GSC beamformer can be expressed as

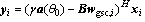                      (3)

where γ is a real constant so as to ensure the convexity of the optimization problem [25], w_gsc,i is the weight vector of the GSC beamformer, the signal blocking matrix 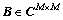requires that 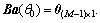According to literature [26], B can be designed as

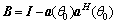                          (4)

Our interest is focused on obtaining the optimum weight vector of the beamformer by using the constant modulus feature and a known DOA of the SOI in order to extract SOI and suppress interferences. Consequently, in the GSC structure, the cost function of the proposed CCM- UKF algorithm can be expressed as

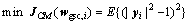               (5)

Obviously, the GSC structure converts the

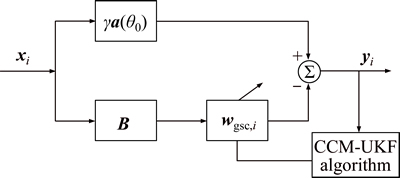
Fig. 1 Blind adaptive beamforming scheme with GSC structure

constrained optimization problem to an unconstrained one. And, the global weight vector w_i can be written as

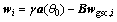                          (6)

3 Proposed CCM-UKF algorithm

In this Section, we firstly change the cost function of the CCM-UKF algorithm into a state space model. Then, the optimum weight vector of the GSC beamformer can be estimated by using the iterative formulas of UKF. The model transformation and implementation procedure of the CCM-UKF algorithm are described as follows in detail.

3.1 Model transformation

If there exists an unknown stationary system w_gsc,I whose array response y_i has the constant modulus feature, according to Eq. (5), we can get two equations below.

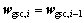                               (7)

                   (8)

If we define that

                  (9)

                      (10)

                 (11)

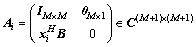             (12)

Equations (7) and (8) can be written as

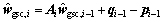                  (13)

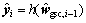                             (14)

where 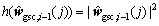is a nonlinear function, 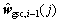is the jth element of .

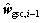By using Eqs. (8) and (14), we can get

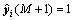                               (15)

The first M elements of 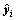have no reference values because is unknown. Consequently, the measure noise v_i is introduced in Eq. (14).

According to Eqs. (7)–(8), (13)–(15), the state space model can be expressed as

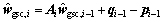                  (16)

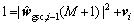                      (17)

Obviously, Eqs. (16) and (17) correspond to the Kalman filter-type structure [22, 27, 28]. We adopt UKF to estimate the optimum weight vector of the GSC beamformer due to its simplicity and effectiveness.

3.2 Implementation procedure of CCM-UKF

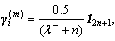
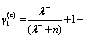
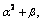
Initialization: α=1, β=2, κ=0, n=M+1, λ^–=α²(n+k– 1)–n+2, 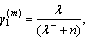the initial state and the initial covariance matrices are 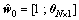and P₀= 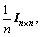respectively. Set the snapshot number and obtain the blocking matrix B according to Eq. (4).

Step 1: the sigma points can be obtained by

             (18)

where is the priori covariance.

Step 2: propagate the sigma points according to the transition matrix A_i

                         (19)

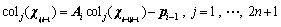 (20)

where 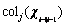is the jth column of .

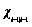Step 3: predict the system state

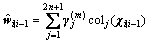                    (21)

Step 4: predict the system covariance matrix

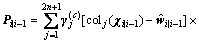
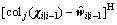                 (22)

Step 5: update the output sigma points

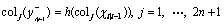         (23)

where 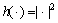is a square operation for each element of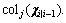

Step 6: predict the system output

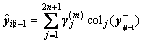                     (24)

Step 7: get the measure covariance matrix

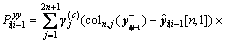
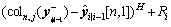          (25)

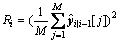                        (26)

where 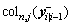is the nth row and the jth column element of 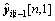is the nth row and the first column element of 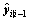. It is hard to set noise parameters in some applications. However, the noise parameters can be adaptively obtained according to literature [22].

Step 8: obtain the cross-variance matrix

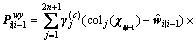
             (27)

Step 9: get the gain matrix

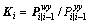                             (28)

Step 10: estimate the system state

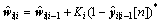                  (29)

Step 11: estimate the error variance matrix

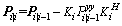                        (30)

Step 12: obtain the weight vector of the beamformer

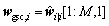                          (31)

Step 13: if it has reached the snapshot number given, stop the programming; otherwise go back to Step 1. The CCM-UKF algorithm flow is summarized in Fig. 2.

4 Proposed RR-CCM-UKF algorithm

In order to reduce computational complexities and increase convergence speeds, some reduced-rank (reduced-dimension) techniques can be applied to the beamforming in such way that the array receiving vector is transformed into a lower dimensional one and we could use optimization methods to obtain the optimum weight vector by operating this vector. Various eigendecomposition-type methods, such as the principal components [29] and the cross spectral metric [30], are utilized to extract the lower dimensional vector. However, the eigen-decomposition operation still requires a high complexity. Consequently, some more effective Krylov- subspace-based methods, such as the multistage Wiener filter (MWF) [31] and the auxiliary vector filter (AVF)[32] (the AVF could be regarded as a special case of the MWF [33]), can show more satisfactory performance. Thus, the reduce-rank technique based on Krylov- subspace is considered adding in the CCM-UKF algorithm in this section.

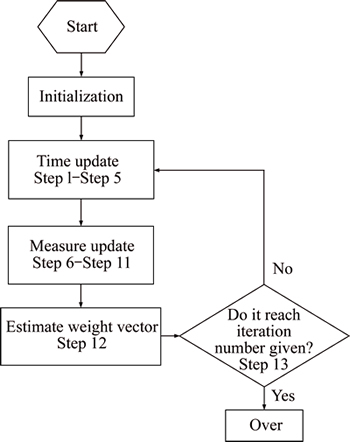
Fig. 2 Flow chart of the proposed CCM-UKF algorithm

4.1 Design of reduced-rank matrix

An illumination of the reduced-rank scheme operating in the GSC structure is shown in Fig. 3. From Fig. 3, we could see that a transformation matrix T is added and the weight vector w_gsc,i becomes its reduced-rank version 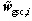compared with those in Fig. 1. It is also easy to verify that the state space model of the RR-CCM-UKF algorithm has a similar form with that of the CCM-UKF algorithm and can be expressed as

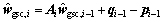                  (32)

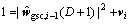                       (33)

where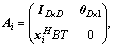

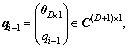
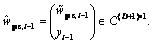
Thus, we can still use UKF to estimate the optimum reduced-rank weight vector .

Fig. 3 Reduced-rank blind adaptive beamforming scheme with GSC structure

According to the Krylov-subspace-based reduced- rank technique, the standard D-dimensional reduced-rank matrix can be constructed as

           (34)

where is the covariance matrix of the received data. There are many methods to choose D [7] [25, 34–36], in this work, we adopt empirical value method due to its effectiveness. Due to the GSC structure, there exists the blocking matrix B that make the below equation be valid

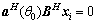                            (35)

Therefore, in case of Eq. (35), we construct the reduced- rank matrix T as

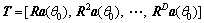            (36)

4.2 Implementation procedure of RR-CCM-UKF

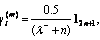
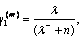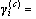
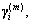
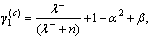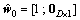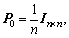Initialization: the dimension number of the filter is n=D+1, some UKF parameters are α=1, κ=0, λ^–=α²(n+κ– 1)–n+2,β=2,the reduced-rank initial state and the reduced-rank initial covariance matrix are and respectively. Obtain the blocking matrix B and set the snapshot number.

Step 1: calculate the reduced-rank matrix by using Eq. (36).

Step 2: obtain the sigma points

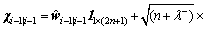
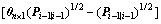          (37)

Step 3: propagate the sigma points by using the reduced-rank transformation matrix A_i in Eq. (32)

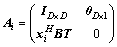                        (38)

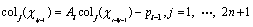    (39)

Step 4: estimate the predicted system state

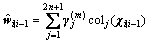                    (40)

Step 5: estimate the predicted system error covariance matrix

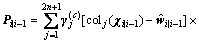
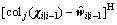                 (41)

Step 6: update the output sigma points

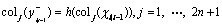         (42)

Step 7: estimate the predicted system output

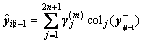                     (43)

Step 8: obtain the measure covariance matrix

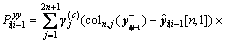
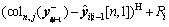          (44)

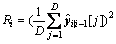                         (45)

Similar to the CCM-UKF algorithm, the noise parameters of the RR-CCM-UKF algorithm are adaptively obtained by using the method in literature [22].

Step 9: estimate the cross-variance matrix

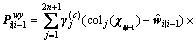
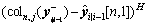             (46)

Step 10: estimate the Kalman gain matrix

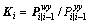                             (47)

Step 11: estimate the updated system state

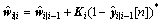                  (48)

Step 12: calculate the error variance matrix

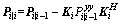                        (49)

Step 13: obtain the reduced-rank weight vector of the GSC beamformer

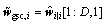                          (50)

Step 14: if it has reached the setting snapshot number, stop the programming; otherwise go back to Step 1. The RR-CCM-UKF algorithm flow is summarized in Fig. 4.

5 Complexity discussion

The computational complexity of the proposed CCM-UKF algorithm is of order O(M³) whereas it is of order O(D³) for the proposed RR-CCM -UKF algorithm by using the reduced-rank technique based on Krylov subspace. The computational complexities of the CCM- RLS and CMV-RLS algorithms are both of order O(M²). Therefore, we can find that the CCM-UKF algorithm has a higher complexity than the CCM-RLS and CMV-RLS algorithms. It is worth emphasizing that the RR-CCM- UKF algorithm can even enjoy the lowest complexity among the four algorithms compared when the number of sensors is large. That is to say that the RR-CCM-UKF algorithm has a lower computational load than the RLS-type methods, if the array dimension number M is enough large and it exists D to make O(D³)2). In addition, in the simulation section, our studies reveal that the steady-state performance of the RR-CCM-UKF algorithm is insensitive to the value of D. Hence, it is easy to choose a suitable value of D to have a lower complexity.

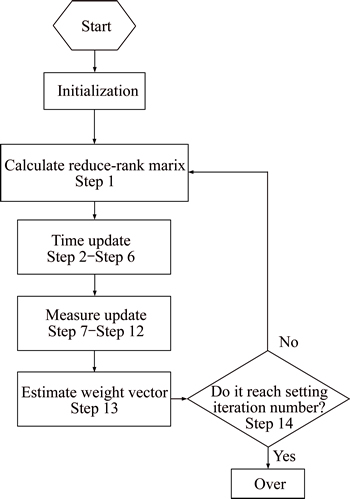
Fig. 4 Flow chart of proposed RR-CCM-UKF algorithm

6 Simulation results

In this section, we evaluate the performance of the proposed algorithms in terms of output SINRs and MSDs for blind adaptive beamforming. Since some literatures [8–12] have demonstrated that the CCM-RLS and CMV- RLS methods are superior to the CCM-SG and CMV-SG algorithms, respectively, the proposed CCM-UKF and RR-CCM-UKF algorithms are just compared with the CCM-RLS and CMV-RLS methods [8, 12] in detail. For comparison, the output SINR of the optimum minimum variance distortionless response (MVDR) is provided as well. The SINR formula is defined as

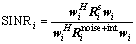                      (51)

where is the auto-correlation matrix of the desired signal 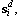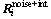is the cross-correlation matrix of the interference and noise signals. The MSD formula is defined as

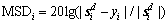                 (52)

Let us consider an ULA with M=12 omnidirectional sensors and the spacing is half-wavelength. The DOA of the SOI is θ₀=10° and it is θ₁=15° for the interference signal. The constant modulus signal model is chosen in accordance with literature [21] as 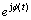(phase f(t) is independently and uniformly distributed over [–π, π]). The power of the Gaussian noise, the SOI and the interference signal is 0.01, 1 and 1, respectively. For each scenario, 50 independent Monte Carlo trials are made to obtain each simulated point.

6.1 Effect of D on RR-CCM-UKF

In this example, we show that how the value of D has an impact on the performance of the proposed RR- CCM-UKF algorithm under different conditions, such as low dimension, high dimension and steering vector with mismatch. For comparison, the numerical result of the CCM-UKF algorithm is presented as well.

In the first experiment, depicted in Fig. 5, we assess the effect of D on the output SINR and MSD of the proposed RR-CCM-UKF algorithm. In particular, the RR-CCM-UKF algorithm with different D is compared with the CCM-UKF algorithm. The number of sensors is M=12. For the RR-CCM-UKF algorithm, the value of D is fixed at 4, 6 and 8, respectively, according to Ref. [36]. It is observed in Fig. 5(a) that the RR-CCM-UKF algorithm with different D has the same steady-state output SINR as the CCM-UKF algorithm, and the convergence speed of the RR-CCM-UKF algorithm with D=4 is faster than its counterparts. Moreover, it also can be noted that the convergence speed of the RR-CCM- UKF algorithm becomes slightly slower with increasing D. Thus, from Fig. 5(a), we see that the value of D has little influence on the steady-state output SINR and a slight impact on the convergence speed for the RR-CCM-UKF algorithm. Figure 5(b) shows the output MSDs of the proposed algorithms versus the number of iterations. In Fig. 5(b), it is seen that the four comparing algorithms are almost the equivalent steady-state MSDs. Furthermore, the convergence speed of the RR-CCM- UKF algorithm becomes slightly faster when decreasing D. Therefore, according to the reduced-rank technique, the convergence speed of the RR-CCM-UKF method is superior to that of the CCM-UKF algorithm no matter in terms of output SINR or MSD in this scenario.

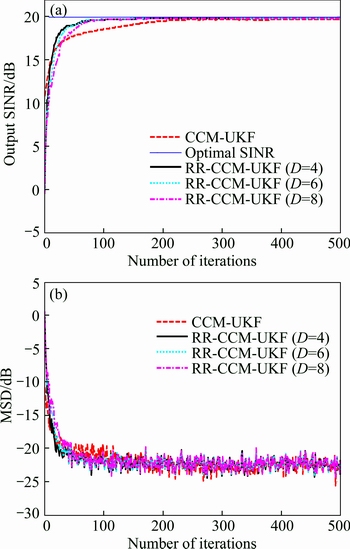
Fig. 5 Results of output SINR (a) and MSD (b) vs number of iterations in experiment

The second experiment have the same parameter settings as the first one except M=32. It is seen in Fig. 6(a) that the RR-CCM-UKF algorithm with different D reaches the steady-state at around 100th iterations that is almost the same as those in Fig. 5(a) while the CCM-UKF algorithm approaches the steady-state at about 400th iterations, which is nearly twice more than those in Fig. 5(a). Moreover, it is also observed that, similar to the first experiment, the convergence speed of the RR-CCM-UKF algorithm with D=4 outperforms those of other algorithms compared. Figure 6(b) shows that, in terms of MSD, the convergence speed of the CCM-UKF algorithm becomes slower than those in Fig. 5(b). Furthermore, we observe that increasing M has little influence on the steady-state MSDs and output SINRs of the proposed CCM-UKF and RR-CCM-UKF algorithms compared with those in Fig. 5. Thus, when the number of sensors is larger, it can lead to a slower convergence performance for the CCM-UKF algorithm. However, due to the reduced-rank technique, there is nearly no discernible difference in terms of convergence speed and SINR as well as MSD for the RR-CCM-UKF algorithm.

In the third experiment, we assume the DOA of the SOI is 11°, but the actual is 10°, .i.e., there exists 1° mismatch in this scenario. The number of sensors is fixed to be M=12. From Fig. 7(a), it is seen that the CCM-UKF algorithm reaches the steady-state at about 200th iterations that is nearly the same as those in the first experiment, and the convergence speed of the RR-CCM-UKF algorithm with D=4 is a little faster than those with D=6 and D=8. However, the steady-state output SINRs of the CCM-UKF and RR-CCM-UKF algorithms drop about 0.3 dB and 1 dB, respectively, compared with those in Fig. 5(a). Therefore, Fig. 7(a) indicates that the DOA of the SOI mismatch lead to a worse output SINR performance for both CCM-UKF and RR-CCM-UKF algorithms, and it is more obvious for the RR-CCM-UKF algorithm than the CCM-UKF algorithm. In other words, the CCM-UKF algorithm has smaller output SINR degradation and better robustness than the RR-CCM-UKF algorithm due to that the latter exists mismatch error in the reduced-rank matrix T in this scenario. In Fig. 7(b), it is also observed that the steady- state MSDs of the CCM-UKF and RR-CCM-UKF algorithms are increased to be –11dB from –23dB in Fig. 5(b) due to the mismatch of the SOI. Thus, in the following experiments, D=4 is chosen for the RR-CCM- UKF algorithm owing to the slightly faster convergence speed.

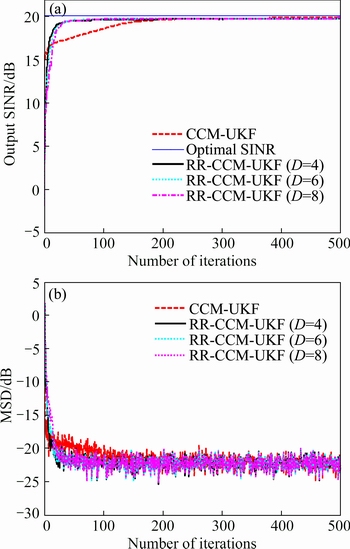
Fig. 6 Results of output SINR (a) and MSD (b) vs number of iterations in experiment 2

Fig. 7 Results of output SINR (a) and MSD (b) vs number of iterations in experiment 3

6.2 Algorithm comparison

In order to verify the effectiveness of the proposed algorithms, three contrast experiments are shown in this example, i.e., the proposed CCM-UKF and RR-CCM- UKF algorithms are compared with the CCM-RLS and CMV-RLS methods under different conditions.

The parameter settings of the fourth experiment are the same as those of the first one. The empirical results of the output SINRs and MSDs of the CCM-UKF, RR-CCM-UKF, CCM-RLS and CMV-RLS algorithms are shown in Fig. 8(a) and Fig. 8(b), respectively. From Fig. 8(a), it is seen that the CCM-UKF and RR-CCM- UKF algorithms approximately provide the same steady- state output SINRs and approach the optimal SINR. We also observe in Fig. 8(a) that the steady-state output SINRs of the CCM-RLS and CMV-RLS solutions are about 17.8 dB and 16.4 dB, respectively, which are obviously smaller than those of the proposed CCM-UKF and RR-CCM-UKF algorithms. Moreover, Fig. 8(a) shows that the CCM-UKF and RR-CCM-UKF algorithms can converge faster than the CCM-RLS and CMV-RLS solutions. From Fig. 8(b), we observe that the CCM-UKF and RR-CCM-UKF algorithms have almost the equivalent steady-state MSDs at –23 dB, which is smaller than those of the CCM-RLS and CMV-RLS solutions. Furthermore, similar to the convergence performance in Fig. 8(a), the CCM-UKF and RR-CCM- UKF algorithms reach the steady-state to require 220 and 100 iterations, respectively, while the CCM-RLS and CMV-RLS algorithms need 400 and 600 iterations, respectively, in Fig. 8(b). This means that the proposed CCM-UKF and RR-CCM-UKF algorithms have faster convergence speeds than their counterparts in terms of MSD. Therefore, the proposed algorithms have larger output SINRs, faster convergence speeds and smaller MSDs than the CCM-RLS and CMV-RLS algorithms in this scenario.

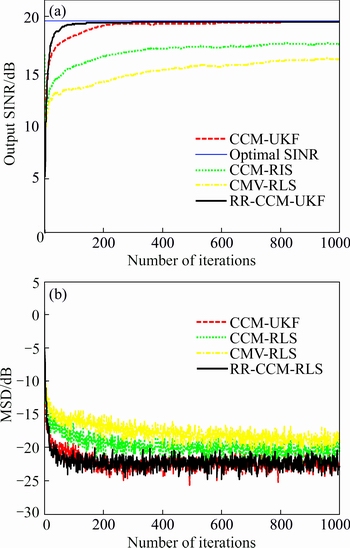
Fig. 8 Results of output SINR (a) and MSD (b) vs number of iterations in experiment 4

In the fifth experiment, the simulation settings are the same as those of the second one. Figure 9(a) shows the output SINRs of the CCM-UKF, RR-CCM-UKF, CCM-RLS and CMV-RLS algorithms versus the number of iterations. It is seen in Fig. 9(a) that, after increasing the number of sensors, the CCM-UKF and RR-CCM- UKF algorithms have nearly the same steady-state output SINRs while those of the CCM-RLS and CMV-RLS methods decrease those, compared with the results in Fig. 8(a). Moreover, from Fig. 9(a), it is also can be observed that the CCM-UKF and RR-CCM-UKF algorithms require around 100 and 400 iterations, respectively, to reach the steady-state. On the other hand, the CCM-RLS and CMV-RLS algorithms need about 700 and 900 iterations, respectively. Hence, it results in slowing the convergence speeds of the CCM-UKF, CCM-RLS and CMV-RLS algorithms that the number of sensors is increased. Figure 9(b) shows that the CCM-UKF and RR-CCM- UKF algorithms arrive at nearly the same steady-state MSDs as those in Fig. 8(b) while the CCM-RLS and CMV-RLS methods increase the MSDs after the number of sensors is increased to be 32. From Fig. 9(b), it also can be observed that, similar to the convergence performance in Fig. 9(a), increasing the number of sensors leads to slowing the convergence speeds of the CCM-UKF, CCM-RLS and CMV-RLS algorithms while there is nearly no influence on the RR-CCM-UKF algorithm due to the reduced-rank technique.

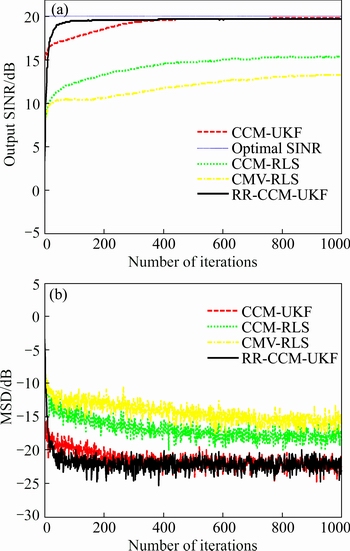
Fig. 9 Results of output SINR and MSD vs number of iterations in experiment 5

In the sixth experiment, the parameter settings of the simulation scenario are the same as those in Fig. 7. The learning curves of the output SINRs of the CCM- UKF, RR-CCM-UKF, CCM-RLS, CMV-RLS algorithms and optimal SINR are shown in Fig. 10(a). It can be observed in Fig. 10(a) that, due to the steering mismatch, the proposed CCM-UKF and RR-CCM-UKF algorithms have slightly output SINRs degradation respectively in different degree, but still keep those at an acceptable level. However, the CCM-RLS and CMV- RLS methods suffer serious performance degradation and make output SINRs to get below 0 dB. Hence, the proposed CCM- UKF and RR-CCM-UKF algorithms have better robustness against steering mismatch than their counterparts. In Fig. 10(b), we can also note that, for all algorithms compared, the steady-state MSDs become larger than those in Fig. 8(b) due to the steering mismatch. However, the proposed CCM-UKF and RR-CCM-UKF algorithms still yield smaller steady-state MSDs compared with the CCM-RLS and CMV-RLS methods. Therefore, the CCM-UKF and RR-CCM-UKF algorithms are superior to the CCM-RLS and CMV-RLS algorithms in the scenario where there exists steering mismatch.

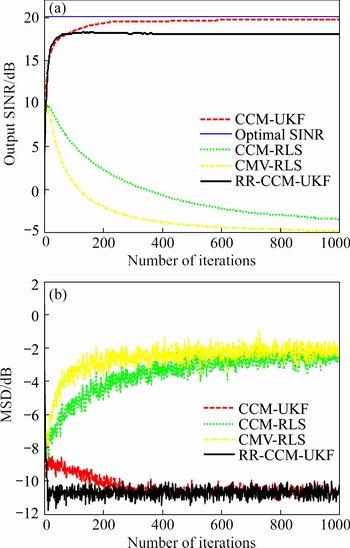
Fig. 10 Results of output SINR (a) and MSD (b) vs number of iterations in experiment 6

7 Conclusions

1) The CCM-UKF and RR-CCM-UKF algorithms for blind adaptive beamforming have been devised in this work. In the GSC structure, we transform the cost function of the constrained optimization problem into a state space model that can be solved by UKF.

2) In order to solve efficiently, the RR-CCM-UKF algorithm is developed by using the Krylov-subspace– based reduced-rank technique and can even require a lower complexity than the RLS-type algorithms in case of large number of sensors.

3) The simulation results demonstrate that, apart from having faster convergence speeds of the weight vector, the proposed CCM-UKF and RR-CCM-UKF algorithms can also provide much larger output SINRs, smaller MSDs and better robustness against steering mismatch than the CCM-RLS and CMV-RLS algorithms.

References

[1] VOROBYOV S A. Principles of minimum variance robust adaptive beamforming design [J]. Signal Processing, 2013, 93(12): 3264–3277.

[2] GODARA L C. Application of antenna arrays to mobile communications. II. Beam-forming and direction-of-arrival considerations [J]. Proceedings of the IEEE, 1997, 85(8): 1195–1245.

[3] YANG Z, DE LAMARE R C, LI X. l1-regularized STAP algorithms with a generalized sidelobe canceler architecture for airborne radar [J]. IEEE Transactions on Signal Processing, 2012, 60(2): 674–686.

[4] VOROBYOV S A, GERSHMAN A B, LUO Z Q. Robust adaptive beamforming using worst-case performance optimization: A solution to the signal mismatch problem [J]. IEEE Transactions on Signal Processing, 2003, 51(2): 313–324.

[5] LIU H, ZHANG Z, LIU D. Adaptive diagonal loaded minimum variance beamforming applied to medical ultrasound imaging [J]. Journal of Central South University, 2015, 22: 1826–1832.

[6] KIM K, PARK S, KIM J, PARK S B, BAE M. A fast minimum variance beamforming method using principal component analysis [J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2014, 61(6): 930–945.

[7] WANG L, DE LAMARE R C, YUKAWA M. Adaptive reduced-rank constrained constant modulus algorithms based on joint iterative optimization of filters for beamforming [J]. IEEE Transactions on Signal Processing, 2010, 58(6): 2983–2997.

[8] DE LAMARE R C, SAMPAIO-NETO R. Blind adaptive MIMO receivers for space-time block-coded DS-CDMA systems in multipath channels using the constant modulus criterion [J]. IEEE Transactions on Communications, 2010, 58(1): 21–27.

[9] WANG L, DE LAMARE R C. Adaptive constrained constant modulus algorithm based on auxiliary vector filtering for beamforming [J]. IEEE Transactions on Signal Processing, 2010, 58(10): 5408–5413.

[10] WANG L, DE LAMARE R C. Robust auxiliary vector filtering algorithm based on constrained constant modulus design for adaptive beamforming [C]// IEEE 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP). Dallas: IEEE, 2010: 2530–2533.

[11] WANG L, DE LAMARE R C. Constrained adaptive filtering algorithms based on conjugate gradient techniques for beamforming [J]. IET Signal Processing, 2010, 4(6): 686–697.

[12] WANG L, DE LAMARE R C. Constrained constant modulus RLS-based blind adaptive beamforming algorithm for smart antennas [C]// IEEE 4th International Symposium on Wireless Communication Systems (ISWCS). Trondheim, Norway, 2007: 657–661.

[13] CAI Y, QIN B, ZHANG H. An improved adaptive constrained constant modulus reduced-rank algorithm with sparse updates for beamforming [J]. Multidimensional Systems and Signal Processing, 2014: 1–20.

[14] SONG N, ALOKOZAI W U, DE LAMARE R C, HAARDT M. Adaptive widely linear reduced-rank beamforming based on joint iterative optimization [J]. IEEE Signal Processing Letters, 2014, 21(3): 265–269.

[15] XU Z, TSATSANIS M K. Blind adaptive algorithms for minimum variance CDMA receivers [J]. IEEE Transactions on Communications, 2001, 49(1): 180–194.

[16] MIGUEZ J, CASTEDO L. A linearly constrained constant modulus approach to blind adaptive multiuser interference suppression [J]. IEEE Communications Letters, 1998, 2(8): 217–219.

[17] JOHNSON R, SCHNITER P, ENDRES T J, BEHM J D, BROWN D R, CASAS R A. Blind equalization using the constant modulus criterion: A review [J]. Proceedings of the IEEE, 1998, 86(10): 1927–1950.

[18] XU Z, LIU P. Code-constrained blind detection of CDMA signals in multipath channels [J]. IEEE Signal Processing Letters, 2002, 9(12): 389–392.

[19] BHOTTO M Z A, ANTONIOU A. A family of shrinkage adaptive-filtering algorithms [J]. IEEE Transactions on Signal Processing, 2013, 61(7): 1689–1697.

[20] ABRAR S, NANDI A K. An adaptive constant modulus blind equalization algorithm and its stochastic stability analysis [J]. IEEE Signal Processing Letters, 2010, 17(1): 55–58.

[21] CHEN Y, LE-NGOC T, CHAMPAGNE B, XU C. Recursive least squares constant modulus algorithm for blind adaptive array [J]. IEEE Transactions on Signal Processing, 2004, 52(5): 1452–1456.

[22] BHOTTO M Z A, BAJIC I V. Constant modulus blind adaptive beamforming based on unscented Kalman filtering [J]. IEEE Signal Processing Letters, 2015, 22(4): 474–478.

[23] QIU L, CAI Y, ZHAO M. Low-complexity variable forgetting factor mechanisms for adaptive linearly constrained minimum variance beamforming algorithms [J]. IET Signal Processing, 2015, 9(2): 154–165.

[24] GRIFFITHS L J, JIM C W. An alternative approach to linearly constrained adaptive beamforming [J]. IEEE Transactions on Antennas and Propagation, 1982, 30(1): 27–34.

[25] DE LAMARE R C, HAARDT M, SAMPAIO-NETO R. Blind adaptive constrained reduced-rank parameter estimation based on constant modulus design for CDMA interference suppression [J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2470–2482.

[26] WERNER S, WITH M, KOIVUNEN V. Householder multistage Wiener filter for space-time navigation receivers [J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 975–988.

[27] WAN E A, VAN DER MERWE R. The unscented Kalman filter for nonlinear estimation [C]// Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000. Lake Louise, Canada: IEEE, 2000: 153–158.

[28] JULIER S J, UHLMANN J K. Unscented filtering and nonlinear estimation [J]. Proceedings of the IEEE, 2004, 92(3): 401–422.

[29] SONG Y, ROY S. Blind adaptive reduced-rank detection for DS-CDMA signals in multipath channels [J]. IEEE Journal on Selected Areas in Communications, 1999, 17(11): 1960–1970.

[30] GOLDSTEIN J S, REED I S. Reduced-rank adaptive filtering [J]. IEEE Transactions on Signal Processing, 1997, 45(2): 492–496.

[31] GOLDSTEIN J S, REED I S, SCHARF L L. A multistage representation of the Wiener filter based on orthogonal projections [J]. IEEE Transactions on Information Theory, 1998, 44(7): 2943–2959.

[32] PADOS D A, BATALAMA S N. Joint space-time auxiliary-vector filtering for DS/CDMA systems with antenna arrays [J]. IEEE Transactions on Communications, 1999, 47(9): 1406–1415.

[33] CHEN W, MITRA U, SCHNITER P. On the equivalence of three reduced rank linear estimators with applications to DS-CDMA [J]. IEEE Transactions on Information Theory, 2002, 48(9): 2609–2614.

[34] SOMASUNDARAM S D, PARSONS N H, LI P, DE LAMARE R C. Reduced-dimension robust capon beamforming using Krylov- subspace techniques [J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 270–289.

[35] XI Z, WU X, WU S, TANG Z, HU S. Low-Complexity robust capon beamforming based on reduced-rank technique [J]. Journal of Electrical and Computer Engineering, 2015, 2015: 3.

[36] HONIG M L, GOLDSTEIN J S. Adaptive reduced-rank interference suppression based on the multistage Wiener filter [J]. IEEE Transactions on Communications, 2002, 50(6): 986–994.

(Edited by HE Yun-bin)

Cite this article as: QIAN Hua-ming, LIU Ke, JIAO Zhi-bo, Ma Jun-da. Blind adaptive constrained constant modulus algorithms based on unscented Kalman filter for beamforming [J]. Journal of Central South University, 2017, 24(10): 2342–2352. DOI:https://doi.org/10.1007/s11771-017-3646-y.

Foundation item: Project(61573113) supported by the National Natural Science Foundation of China; Project(2014RFXXJ074) supported by the Science and Technology Innovation Talents Research Fund of Harbin, China

Received date: 2016-02-25; Accepted date: 2016-07-11

Corresponding author: LIU Ke, PhD Candidate; Tel: +86–18003661983; E-mail: liuke_heu@163.com