
Finite element analysis of γ′-phase raft mechanism in
Ni-based single crystal superalloy
WU Wen-ping(吴文平), GUO Ya-fang(郭雅芳), WANG Yue-sheng(汪越胜)
Institute of Engineering Mechanics, Beijing Jiaotong University, Beijing100044, China
Received 28 July 2006; accepted 15 September 2006
Abstract: The finite element method was applied to study the mechanics of rafting of γ′ precipitates in a single crystal Ni-based superalloy with the [001] orientation. The results show that the creep and rafting are closely related with the stress and strain energy density distributions in the matrix channels. The application of an external stress leads to differential levels of von Mises stress and strain energy density, and the largest value of the stress appears at the corners of the matrix near the interface. Creep dislocations penetrate preferentially into the most highly stressed matrix channels where the γ′-phase rafting is also enlarged. Meanwhile, the von Mises stress of γ matrix and γ′ precipitate increases with the increase of temperature, thus the rafting becomes easier at a higher temperature. Moreover, according to the analysis of slip systems for the Ni-based superalloy, the critical external load for bowing a dislocation through a matrix channel at 950 ℃ is about 180 MPa, which is consistent with the related experimental results.
Key words: Ni-based superalloy; rafting; creep dislocation; critical external load; finite element analysis
1 Introduction
Ni-based single crystal superalloys are widely used as engine turbine blade materials for their excellent creep resistance behavior. They are strengthened by a high volume fraction of hard cubical γ′ precipitates embedded coherently in a softer γ matrix. When superalloys are subjected to creep at high temperatures, typically above 850 ℃, the γ′ particles coarsen directionally to form rafts generally aligned along the [001] direction[1-2]. The rafting of γ′ precipitates under the influence of an applied stress was first studied by TIEN et al[3]. Subsequently, the mechanisms of rafting and its influence on the creep resistance of superalloys have been widely studied by experiments and calculations[4-9]. Recently, a number of finite element computations have been applied for describing and predicting the raft morphology. SHA et al[10] and TIAN et al[11] calculated the stress distribution in matrix channels and discussed the driving force for the γ′ rafting by finite element analysis. ZHOU et al[12] applied the finite element method to study the stress and energy density distributions around γ′ before coarsening loaded in the [110] direction in Ni-based superalloy. In this study, we aimed to investigate how the elastic strain energy density and von Mises stress were affected by the temperature and external tensile stress applied along [001] direction. Moreover, the critical external loads for bowing a dislocation through a matrix channel and the developing of the creep at different temperatures were specially discussed.
2 Numerical models
Because of the cubic symmetry of the micro-
structure, it is only necessary to consider one quarter of the γ′ precipitate and the surrounding matrix as shown in Fig.1. The γ′ precipitates with the cubical shape are uniformly distributed in the γ matrix, and the volume fraction of the γ′ phase is 70%. The C11, C12, and C44 are selected from Refs.[10-11], their elastic constants of the γ′ precipitates and the γ matrix are listed in Table 1. In the finite element modeling, generalized plane strain elements are used because they provide a better approximation of the three dimensional problem compared with the plane strain or plane stress analysis, by permitting uniform strains to develop within the “thickness” dimensional of the model. Due to symmetry considerations, the upper and right boundaries of the domain were constrained to remain on a plane, and the nodes along bottom and left boundaries were permitted to move only in the x and y directions, respectively. The tensile stress is applied along y direction. The difference between the lattice parameters  and αγ of the two cubic structures is measured by the lattice misfit defined by
and αγ of the two cubic structures is measured by the lattice misfit defined by
 (1)
(1)
where αγ=1.60×10-5 K-1,  =1.29×10-5 K-1. So δ=-0.26% at 950 ℃. In our calculation, we use a thermal expansion method to realize the effect of lattice
=1.29×10-5 K-1. So δ=-0.26% at 950 ℃. In our calculation, we use a thermal expansion method to realize the effect of lattice
misfits. The finite element calculation is performed with the ANSYS software code.
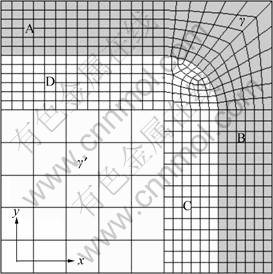
Fig.1 Finite element model
Table 1 Stiffness Cii of matrix and precipitate phase at 950 ℃ (1011 Pa )

After the FE calculation, the elastic strain energy density (G) of each element is obtained by
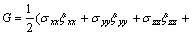
 (2)
(2)
The von Mises stress σe is given by

 (3)
(3)
3 Results and discussion
3.1 Distributions of internal stress and strain energy at tensile stress along [001] direction
The matrix channel parallel to the stress axes direction is defined as parallel channel (PC), while the matrix channel vertical to the stress axes direction is defined as vertical channel (VC). We can see in Fig.2(a) that the von Mises stress distributions in the PC are identical as those in the VC (symmetrical distribution) when no external stress is applied. The von Mises stress in the precipitate is also symmetrically distributed as shown in Fig.2(b), but the value of the stress is much lower than that in the matrix. Moreover, the distributions of the elastic strain energy density in the matrix and precipitate are similar to those of the internal stress.
In Figs.3 and 4, the tensile stress of 300 MPa along the [001] direction is applied to a negative misfit alloy. The results indicate that the application of an external stress leads to differential levels of von Mises stress and strain energy density in the γ matrix and γ′ precipitate. Within the γ matrix in Fig.3(a), the von Mises stress in VC is much larger than that in PC, and the largest value of it is at the corners of the γ matrix near the interface. Within the γ′ precipitate in Fig.3(b), the von Mises stress has also an unsymmetrical distribution, but the change of the von Mises stress after the external stress applied is smaller compared with that in the matrix. A similar event occurs in the elastic strain energy density G as shown in Fig.4.
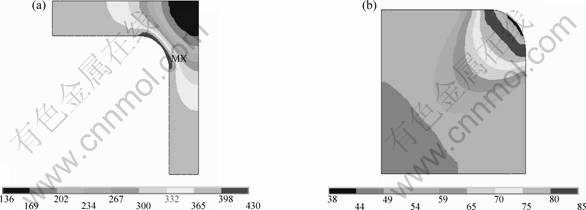
Fig. 2 Von Mises stress σe without external stress applied at 950 ℃ in γ matrix(a) and γ′ precipitate(b)(Units: MPa)

Fig. 3 Von Mises stress σe with external tensile stress applied at 950 ℃ in γ matrix(a) and γ′ precipitate(b)(Units: MPa)
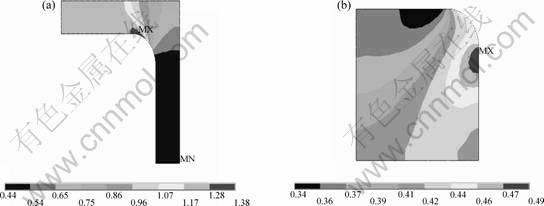
Fig. 4 Strain energy density G with external tensile stress applied at 950 ℃ in γ matrix(a) and γ′ precipitate(b)(Units: J/m3)
Based on the above results,we find that the lattice misfit stress is higher and it is symmetrically distributed when no external stress is applied. In the case of a tensile stress applied to a superalloy with a negative misfit, although the calculation is in the elastic regime, the largest von Mises stress is about 509 MPa in horizontal matrix channel, which is much higher than that in vertical matrix channel. Similarly, the distribution of the strain energy density for negative misfit under external tensile stress is similar to that of the von Mises stress. Due to the higher von Mises stress in horizontal matrix channel(VC), the creep dislocations would generate and distribute predominantly in that region. Meanwhile, the elastic strain energy density is larger in this region, thus the driving force for the dislocation nucleation is higher in the same region. After the dislocations generate and distribute in the horizontal matrix channel, the higher internal stress in that region is relaxed. The creep dislocations penetrate preferentially into the most highly stressed matrix channels where γ′-phase raft is also enlarged.
3.2 Influence of temperature on distribution of internal stress
In order to study more carefully the influence of the temperature on the raft and creep, we calculate the distribution of the internal stress varying with the change of the temperature. Four representative regions A, B, C and D are selected respectively in PC, VC and the precipitate as shown in Fig.1.
From Fig.5(a), we can see that the von Mises equivalent stress σe of selected regions both in the γ matrix and γ′ precipitate increases with the increase of the temperature when no external stress is applied.
After the external tensile stress of 300 MPa is applied, the von Mises stress of region A in the γ matrix and regions C and D in the γ′ precipitate increases with increasing temperature, and the magnitudes are changed greatly. For instance, the average stress of region A (from the temperature of 900 ℃ to 1 050 ℃) in the horizontal matrix increases from about 340 MPa to 480 MPa, and the average stress of region D in the precipitate increases from about 55 MPa to 145 MPa. Whereas for region B in the vertical matrix channel, as shown in Fig.5(b), the value of the equivalent stress σe decreases with the increase of the temperature. Because region B lies in the vertical matrix channel (PC), its misfit stress and external stress weaken one another. The increase of the equivalent stress due to the temperature increasing cannot balance the effect of the interaction between the misfit stress and external stress. Therefore, for an alloy with the negative misfit under external tensile stress, the internal stress in the vertical matrix decreases with increasing temperature. It should be emphasized that the elastic constants decrease with increasing temperature, but its effect on the internal stress state is smaller compared to the influence of the lattice misfit. At a higher temperature, the von Mises stress of γ matrix and γ′ precipitate increases with the increase of the temperature. Meanwhile, the internal fractional stress for dislocation movement decreases with increasing temperature. Therefore, the creep and γ′ precipitates rafting become easier at a higher temperature.
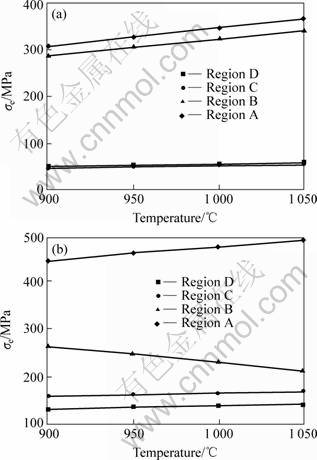
Fig.5 Relationships between σe of selected regions and temperature: (a) No external stress; (b) Applying 300 MPa external tensile stress
3.3 Critical external loads for bowing dislocation through matrix channel
Fig.6 shows the change of the von Mises equivalent stress σe of the selected regions varying with the increase of the external tensile stress at 950 ℃. For regions A, C and D, the magnitude of σe increases with the increase of the external tensile stress; whereas for region B in the vertical matrix channel, its change is reversed. This behavior is closely related with characteristics of the misfit. The misfit stress in the vertical matrix is compressive when the external tensile stress is applied along [001] direction, thus the misfit stress in the vertical matrix and external stress weaken one anther. However, the misfit stress in the horizontal matrix channel is exactly reversed. Region A locates in the horizontal matrix channel, so the von Mises equivalent stress σe increases with the external tensile stress increasing.
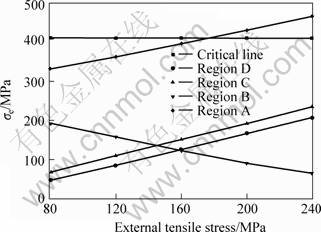
Fig.6 Relationships between σe of selected regions and external tensile stress at 950 ℃
As we know, there are three slip system clans in the nickel-based crystal for dislocation movement: a cubical slip system clan, including six slip systems; an octahedral slip system clan, including twelve slip systems; and a dodecahedral slip system clan, including twelve systems. Dislocation movement starts easily in the octahedral slip system clan along the [001] direction when a one external stress is applied[13]. The critical shear stress, which is required for bowing a dislocation through a matrix channel, is given by
 (4)
(4)
Where μ is the shear modulus (equals 41.0 GPa), b is the Burgers vector (equals 0.25 nm),  is the largest channel dimension in the slip plane and
is the largest channel dimension in the slip plane and  is the actual matrix channel width along the cube direction (equals 50 nm).
is the actual matrix channel width along the cube direction (equals 50 nm).
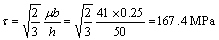
A shear stress of 167.4 MPa is required for dislocation bowing through the channel.
Considering the relationship between the creep stress and the critical shear stress yields:
Τ=Sfσ (5)
Where the Schmidt factor  [14]. Then
[14]. Then
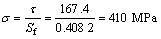
Thus a minimum uniaxial stress of 410 MPa is required for bowing a dislocation through an average matrix channel at 950 ℃.
From Fig.6, we find that the von Mises equivalent stress of region A in the horizontal matrix channel first reaches the creep critical stress at an external stress of about 180 MPa. According to the discussion of section 3.1 that the creep penetrates preferentially into the most highly stressed matrix channel, then a critical external stress for the onset of a creep dislocation in the horizontal matrix channel is obtained. We can assume that the critical external tensile stress of about 180 MPa is required for bowing a creep dislocation in the horizontal matrix channel at 950 ℃. The related experimental results have been obtained by POLLOCK et al on CMSX-3[13].
4 Conclusions
1) The application of an external stress leads to differential levels of von Mises stress and strain energy density in the matrix and precipitates. The largest value of the stress appears at the corners of the matrix near the interface, where the creep dislocations are preferred to generate.
2) The von Mises stress of γ matrix and γ′ precipitate increases with the increase of the temperature. Thus the creep and γ′ precipitates rafting become easier at a higher temperature.
3) According to the analysis of the slip systems in Ni-based superalloy, the critical external load for bowing a creep dislocation through a matrix channel at 950 ℃ is about 180 MPa, which is consistent with the related experimental results.
References
[1] BUFFIERE J Y, IGNAT M. A dislocation based criterion for the raft formation in nickel-based superalloys single crystals[J]. Acta Metall Mater, 1995, 43: 1791-1797.
[2] NABARRO F R N. Raft in superalloy[J]. Metall Mater Trans, 1996, A27: 513-530.
[3] TIEN J K, COPLEY S M. The effect of uniaxial stress on the periodic morphology of coherent gamma prime precipitates in nickel-base superalloy crystals[J] Metall Trans, 1971(2): 215-219.
[4] SOCRATE S, PARKS D M. Numerical determination of the elastic driving force for directional coarsening in Ni-superalloys[J]. Acta Metall Mater, 1993, 41: 2185-2193.
[5] ZHANG J X, WANG J C, HARADA H, KOIZUMI Y. The effect of lattice misfit on the dislocation motion in superalloys during high-temperature low-stress creep[J]. Acta Mater, 2005, 53: 4623-4633.
[6] YASHIRO K, KUROSE F, NAKASHIMA Y, KUBO K, TOMITA Y, ZBIB H M. Discrete dislocation dynamics simulation of cutting of γ′ precipitate and interfacial dislocation network in Ni-based superalloys[J]. International Journal of Plasticity, 2006, 22: 713-723.
[7] OHASHI T, HIDAKA K, IMANO S. Elastic stress in single crystal Ni-base superalloys and the during force for their microstructural evolution under high temperature creep conditions[J]. Acta Mater, 1997, 45: 1801-1810.
[8] MULLER L, GLATZEL U, FELLER-KNIEPMEIER M. Calculation of the internal stresses and strains in the microstructure of a single crystal nickel-base superalloy during creep[J]. Acta Metall Mater, 1993, 41: 3401-3411.
[9] TIEN J K, COPELY S M. The effect of orientation and sense of applied uniaxial stress on the morphology of coherent gamma prime precipitates in stress annealed nickel-base superalloy crystals[J]. Metall Trans, 1971, 2: 543-553.
[10] SHA Yu-hui, CHEN Chang-rong, ZHANG Jing-hua, XU Yong-bo, HU Zhang-qi. Orientation dependence of directional coarsening behavior in a nickel-base single crystal superalloy[J]. Acta Metall Sin, 2000, 36(3): 258-261.(in Chinese)
[11] TIAN Su-gui, CHEN Chang-rong, YANG Hong-Cai, HU Zhang-qi. Finite element analysis of diving force of γ′-phase directional coarsening for a single crystal nickel-base superalloy during high temperature creep[J]. Acta Metall Sin, 2000, 36(5) 465-471.(in Chinese)
[12] ZHOU L, LI S X, CHEN C R, WANG Y C, ZANG Q S, LU K. Three-dimensional finite element analysis of stresses and energy density distributions around γ′ before coarsening loaded in the [110]- direction in Ni-based superalloy[J]. Materials Science and Engineering, 2003, A352: 300-307.
[13] POLLOCK T M, ARGON A S. Directional coarsening in Nickel-base single crystals with high volume fractions of coherent precipitates[J]. Acta Metall Mater, 1994, 42: 1859-1874.
[14] YU Qing-min, WAN Jing-sheng, YUE Zhu-feng. Development of Marc user subroutine for creep analysis of nickel-based single crystal blade[J]. Gas Turbine Experiment and Research, 2004, 17(4): 20-23. (in Chinese)
(Edited by YANG You-ping)
Foundation item: Projects(10572019, 10672016)supported by the National Natural Science Foundation of China; project(2005SM0035) supported by
the Science Foundation of Beijing Jiaotong University, China
Corresponding author: GUO Ya-Fang; Tel: +86-10-51682094; E-mail: yfguo@center.njtu.edu.cn