提取相位和方向特征的手指静脉识别方法
王科俊,刘靖宇,杨晓菲
(哈尔滨工程大学 自动化学院,黑龙江 哈尔滨,150001)
摘要:针对静脉纹路具有较强方向性的结构特点,提出一种提取手指静脉相位和方向特征进行识别的新方法。首先,用2D-Gabor滤波器对原始静脉图像进行滤波,提取相位和方向的纹理信息,在特征级上融合成编码,用改进的Hamming距离进行匹配。该方法不要求对指静脉图像做前期处理和定位,简单易行,并且在一定程度上可以克服图像平移和旋转对识别结果的影响,能够快速准确地进行身份识别,误识率为1.65%,具有实际应用价值和发展前景。
关键词:静脉识别;参数选择;相位和方向特征
中图分类号:TP391.41 文献标志码:A 文章编号:1672-7207(2011)S1-0794-06
A method for extracting phase and orientation information for finger vein recognition
WANG Ke-jun, LIU Jing-yu, YANG Xiao-fei
(College of Automation, Harbin Engineering University, Harbin 150001, China)
Abstract: Based on directional and structural characteristics of finger vein, a novel algorithm to extract phase and directional features is proposed. Firstly, a 2D-Gabor filter is used to filter the original finger vein image in order to extract phase and directional texture features; a code is then used for feature level fusion; and finally, a modified Hamming distance matching is performed. This method is simple and does not require pre-processing image. It is also invariant to translation and rotation and performs with a fast and accurate recognition. It has a false acceptance rate of 1.65%.
Key words: vein recognition; preferences; phase and orientation code
手指静脉识别是模式识别领域的前沿课题,具有稳定性、非接触式、活体特征提取、高防伪性和高精度等优点,具有广阔的发展前景。在国外,日本的日立公司对手指静脉识别研究起步较早,其产品应用于银行、安检等高安全等级的场合。Miura等[1]提出了一种基于模板匹配的静脉识别方法。先将图像进行二值化,并对二值化后的图像进行距离变换,去除了大量的无信息向量;最后,应用嵌入式隐马尔可夫模型对指静脉进行识别。但识别速度很慢,手指若有较大变形则不能准确识别。国内手指静脉识别技术的研究还处于起步阶段,但发展很快。王科俊等[2]采用一种融合小波矩和PCA分解及LDA变换的方法对手指静脉进行识别,将手指静脉图像矩阵转化为一维向量进行降维处理。这是目前手指静脉识别领域中效果较好的一种方法。李雪妍[3]提出了一种采用二维小波分析与纹理特征相结合的方法实现了手指静脉识别。钱晓 华[4]提出用7个不变矩作为手指静脉特征,利用欧式距离和阈值分类准则对静脉进行匹配。上述几种方法在解决特定的手指静脉识别问题方面各有优点,但由于手指静脉没有明显的周期性纹理;有效信息集中在低频部分;指静脉图像灰度分布不均;静脉细小,可提取特征;采集时手指的平移和旋转都会对识别结果产生影响。针对上述问题,本文作者提出了一种融合相位和方向特征的方法对手指静脉进行识别。由于手指静脉图像纹路是由多条线组成的,具有明显并稳定的方向性,可看作是纹理图像。二维Gabor滤波器属于二维连续小波变换,被广泛用于提取图像的纹理特征。Daugman[5]在1985年阐述了它的性质:二维Gabor滤波器能达到空间和频率的最优分辨率。这些性质对图像的纹理分析特别有效。这种方法已在掌纹识别[6] 和虹膜识别[7]中得到成功的应用。
为此,考虑到手指静脉也具有明显的方向性和局部特性,本文作者提出了一种新的手指静脉识别方法。该方法用4个不同方向上的二维Gabor滤波器对原始静脉图像进行滤波,分别提取相位和方向的纹理信息,并将这些特征进行融合,形成编码,最后用改进的Hamming距离来衡量不同编码之间的相似性。该方法不要求对图像进行预处理和定位,可以在一定程度上克服手指变形,平移和旋转带来的影响。根据手指静脉的形状和结构特性,给出了一种适合纹理特征提取的二维Gabor滤波器参数的设置方法,提高了手指静脉识别的精度。实验结果表明:该方法能够快速准确地进行身份识别,具有一定的实际应用价值。
1 相位和方向特征提取
二维Gabor滤波器[8]实际上是高斯函数经复指数函数调制后形成的滤波器,定义如下:

 (1)
(1)
式中:自变量x,y是图像I(x,y)各像素点的直角坐标值,若图像大小为M×N,则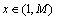 ,
,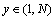 ;θ是滤波器的方向;μ是复正弦函数的频率;σ是高斯包络沿x轴和y轴方向的标准方差。
;θ是滤波器的方向;μ是复正弦函数的频率;σ是高斯包络沿x轴和y轴方向的标准方差。
由于滤波器的虚部是奇对称的,所以其直流分量为0。滤波器的实部通过下式可将其直流分量归一化成0:

 (2)
(2)
式中:滤波器的大小为(2n+1)2。归一化后,滤波器的实部与虚部的直流分量都为0,这样使得滤波的结果受光照强度的影响非常小。
式(1)经过整理,得到它的实部和虚部分别如式(3)和(4)所示:
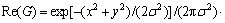
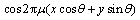 (3)
(3)
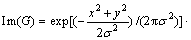
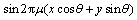 (4)
(4)
下面用二维Gabor滤波器对原始静脉图像进行滤波。选取4个频率和方差均相同但方向不同的滤波器,提取静脉的相位和方向信息。
设I是一幅静脉图像,用4个滤波器Gj(j=0,1,2,3)对I进行滤波:
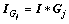 (5)
(5)
定义滤波后的图像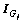 的幅值如下:
的幅值如下:
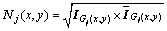 (6)
(6)
式中: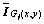 表示
表示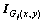 的复共轭。
的复共轭。
点(x,y)的方向定义为:
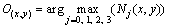 (7)
(7)
式中:O(x,y)称为静脉图像I的在点(x,y)的方向码。
静脉的相位特征码包括实部特征和虚部特征,可以通过下式计算得到:
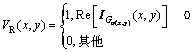 (8)
(8)
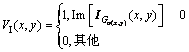 (9)
(9)
手指静脉的实部、虚部和方向码这3种特征,反映了静脉的不同特性。如果把这3种特征分别进行识别操作,会存在大量孤立点,破坏静脉结构的整体性。所以,把提取出的相位和方向特征进行融合,既形成了新的整体特征,给出了决策分析所需要的信息,又保留了原始信息。融合后的特征表示如下:
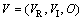
式中:VR,VI和O分别表示手指静脉特征的实部,虚部和方向部分。
2 相位和方向特征码的匹配
在采集静脉图像时,每个图像的位置和角度不完全相同,使截取后的图像包含了一些背景,这些背景的存在会影响匹配结果。因此,在匹配前应进行图像分割。这里用一个二值矩阵作为掩模。设静脉图像I的掩模M可用下式计算:
 (10)
(10)
式中:T为阈值。
假设图像I1和I2为2幅手指静脉图像,M1和M2为对应掩模。进行匹配时,只对M1和M2均为1的点进行匹配,结果可用二值图像M来表示:
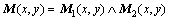
式中:“ ”是逻辑“与”操作。
”是逻辑“与”操作。
令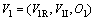 ,
, 代表图像I1和I2的相位方向码。V1R和V2R,V1I和V2I的差异可用二值图像HR和HI分别表示,公式如下:
代表图像I1和I2的相位方向码。V1R和V2R,V1I和V2I的差异可用二值图像HR和HI分别表示,公式如下:
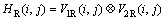 (11)
(11)
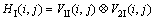 (12)
(12)
式中:“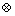 ”表示逻辑“异或”操作。
”表示逻辑“异或”操作。
O1和O2的差异可用如下二值图像Ho来表示:
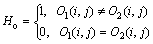 (13)
(13)
静脉图像的相位方向码V1和V2的相似性可用如下的Hamming距离来表示:

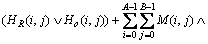
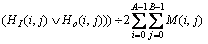 (14)
(14)
式中:A和B是静脉图像I的行数和列数;“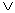 ”代表逻辑“或”运算。显然,D(V1,V2)的值在0和1之间,值越小,V1和V2的相似性越高。反之,二者的相似性越低。
”代表逻辑“或”运算。显然,D(V1,V2)的值在0和1之间,值越小,V1和V2的相似性越高。反之,二者的相似性越低。
3 手指静脉的相位和方向码实例
3.1 滤波器参数选取
二维Gabor滤波器实现的难点是滤波器组的参数选择。目前,Gabor滤波器的参数设置还没有统一的标准。针对手指静脉的纹理特征,本文作者通过分析滤波器中各参数对滤波器性能的影响,进行大量实验,通过调整一系列参数得到了不同方向、频率和方差的滤波器,选取一组与手指静脉纹理的分布特点相接近的滤波器,提取手指静脉的纹理特征。
式(1)中,θ的取值个数对Gabor滤波器的输出结果可产生直接的影响。对于纹理分析目的,不需要选择覆盖整个频域的滤波器参数空间。考虑到Gabor滤波器在频域内具有共轭对称性,只需要在[0,π]内选择方向参数即可。而θ的变化是连续的,需要合理的离散的均匀采样。因此,通常选取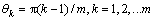 [9],m代表所选取方向的个数。本文选取的k=4,则θ分别为0°,45°,90°,135°。
[9],m代表所选取方向的个数。本文选取的k=4,则θ分别为0°,45°,90°,135°。
n的选取决定了滤波器的大小,过大则不能体现滤波器的局部化特性;过小则会使波形不完整。而手指表面成曲面状,手指静脉细长、平直,本文提取矩形区域为滤波器作用的有效区域。经过大量的实验验证,当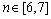 时,能够获得完整的波形,并能体现局部特性。
时,能够获得完整的波形,并能体现局部特性。
σ决定了高斯包络的扩展,体现局部特征的变化。手指静脉本身非常细小,尤其是静脉的交叉处,细节特征丰富。σ选取越小,提取的局部特征越多。若取得过小,则会出现噪声。在此选取滤波器的参数 进行滤波提取静脉的微观结构信息。
进行滤波提取静脉的微观结构信息。
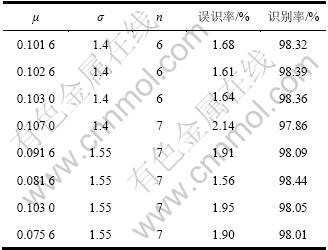
μ决定了Gabor滤波器的频率选择特性,滤波器根据μ的不同产生不同的震荡频率,体现全局特征。手指静脉的粗细不同,纹路和灰度分布不均,对比度较低。若μ太大,滤波过程将会产生虚假纹线;反之,若μ太小,相邻的纹线则会合并到一起。本文作者通过先验知识和大量实验,给出了参数μ的选择区间。在设计滤波器参数时,可以根据表1所示的参数区间取值,选取一组滤波器。从表1可以看出,在μ=0.816,σ=1.55,n=7时,识别率最高。本文将以这组参数作为滤波器的参数,对手指静脉图像进行滤波。
表1 不同滤波器参数对应的识别率
Table 1 Different filter parameters corresponding to recognition rate
3.2 手指静脉的相位和方向码
经过切割之后的原始静脉图像的大小为100×220像素,96 dpi,占用空间约4 000个字节。根据文献[9]的方法,不需要对静脉图像上的所有点进行匹配。该方法每隔4点采样1次,仅取25×55像素。为了消除静脉图像平移和旋转的影响,在水平方向上进行-5到+5个像素的平移,在竖直方向上进行-5到+5个像素的平移。然后把各个位置上的相位方向码与其他相位方向码进行匹配,最后在这些匹配距离中,选择一个海明距离最小的作为最终的匹配距离。
图1所示为3幅手指静脉图像经过滤波器滤波之后得到的相位和方向部分的纹理图像。(1)和(2)是同源手指静脉图像;(2)和(3)是非同源手指静脉图像。可以清晰地看到手指静脉深层次的纹理走向以及不同静脉之间的纹理差别。表2列出了图1中样本两两比对的海明距离。可见:(1)和(2)的海明距离较小;(2)和(3)的海明值较大。说明该方法对手指静脉识别是有效的。

图1 手指静脉的相位和方向特征码
Fig.1 Direction and phase signature of finger vein
表2 匹配距离
Table 2 Matching distance in Fig.1

4 实验结果与分析
在手指静脉数据库中,选用314人的手指静脉图像,每人的手指(食指)都采集1次,共314幅图像,构成训练库。另外,每人另采集4幅,共1 256幅,组成静脉测试库。
4.1 手指静脉匹配
将训练库中的每个样本都与其他样本进行匹配,一共进行49 241次,其中314次为合法匹配,其余为非法匹配。得到2种不同的验证曲线,如图2所示。横轴表示海明距离,纵轴表示匹配所得的对应海明距离样本的概率密度。实曲线表示合法匹配曲线,虚曲线表示非法匹配曲线,他们都类似于高斯分布。合法匹配的匹配距离均值对应于横轴0.25附近的波峰,非法匹配的匹配距离均值对应于横轴0.60附近的波峰。二者波峰相距较远,交叉不多。可见,本方法能有效地区分不同的手指静脉。当阈值在[0.1,0.4]区间时,识别准确率最高。
在1:1验证模式下,将验证库中的每一幅样本都和测试库中对应的同源样本作比对,进行验证实验。实验结果如表3所列。对于1:n的识别模式,用测试库中的每个样本都与训练库中的所有样本作比对,进行测试,实验结果如表4所列。
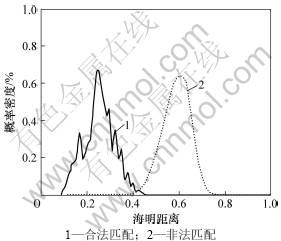
图2 合法匹配与非法匹配的匹配距离分布
Fig.2 Matching distance distribution of legal and illegal matching
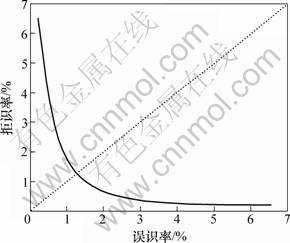
图3 手指静脉的相位和方向码的ROC曲线
Fig.3 ROC curve of phase and direction of finger vein code
表3 1:1模式下拒识率测试结果
Table 3 Tested rejection rates of 1:1 mode

表4 1:n模式下误识率测试结果
Table 4 Tested error rates of 1:n mode

实验结果表明,该方法在手指静脉上的尝试达到了比较理想的效果。
4.2 图像的平移和旋转测试
由于采用非接触式采集方式,会不可避免地出现一些平移和旋转现象,手指位置变化的自由度为4,影响了识别结果。而本文的方法可以在一定程度上克服平移和旋转对识别的影响。
为了验证本方法的效果,把测试库中的1 256个样本分别在[-5,+5]个像素内随机均匀平移和在[-5°,+5°]内随机均匀旋转(在平面内旋转),组成平移测试库和旋转测试库。分别用这2个测试库的每个样本与训练库中的同源样本进行对比,完成1:1验证实验;分别用这2个测试库的每个样本与训练库中的所有样本进对比,完成1:n识别实验。实验结果如表5~ 8所示。
实验结果表明,当图像在一定程度上进行平移和旋转时,系统仍能保持稳定的识别率,可以满足实际应用的要求。另外,根据文献[1]提出的模板匹配方法, 采用本文使用的静脉库中的图像,用相同的方法进行验证和识别实验。在1:1验证模式下,拒识率为2.90%。在1:n识别模式下,误识率为3.30%。鉴于算法实现过程中的误差和采用图像的质量不同,识别结果与原文相比存在一定的误差。当模板存在较大变形时,识别效果不佳。
表5 平移测试库的验证测试结果
Table 5 Verification test results of translation database

表6 平移测试库的识别测试结果
Table 6 Identification test results of translation database

表7 旋转测试库的验证测试结果
Table 7 Verification test results of rotating database

表8 旋转测试库的识别测试结果
Table 8 Identification test results of rotating database

4.3 存储量和速度分析
相位码的实部和虚部为25×55的二值矩阵,这两部分的存储量[(25×55)/8]×2≈344(字节);方向部分为25×55的矩阵,存储量为[(25×55×2)/8]≈344(字节);掩模也为25×55的二值矩阵,存储量为[(25×55)/8]≈172(字节)。所以,一个手指静脉模板的存储量为344+344+172=860(字节),低于原始图像的存储量。完成一次身份识别需要0.907 s。该方法的系统响应时间可以达到实际应用的生物识别系统的要求。
5 结论
本文提出了一种提取相位及方向特征的手指静脉识别方法,用4个二维Gabor滤波器对原始静脉图像进行滤波,提取静脉的相位和方向信息,将这些特征进行融合,形成编码,最后用改进的海明距离来衡量不同编码之间的相似性。测试结果表明,该方法能够有效地区分不同的手指静脉图像,在一定程度上可以克服图像平移和旋转对识别结果带来的影响。由于是对原始静脉图像直接进行提取相位和方向特征,克服了一般静脉识别方法需要复杂的预处理和定位工作的缺点,大大减少了工作量,提高了效率;同时,该方法所需存储空间较小。在以后的研究中,将致力于改进二维 Gabor滤波器的性能,并对参数进行优化,提高手指静脉识别的可靠性。
参考文献:
[1] Miura N, Nagasaka A, Miyatake T. Feature extraction of finger-vein patterns based on repeated line tracking and its application to personal identification[J]. Machine Vision and Applications, 2004, 15(4): 194-203.
[2] 王科俊, 袁智. 基于小波矩融合PCA变换的手指静脉识别[J]. 模式识别与人工智能, 2007, 10(5): 692-697.
WANG Ke-jun, YUAN Zhi. Finger vein recognition based on wavelet moment fused with PCA transform[J]. Pattern Pecongnition and Artificial Intelligence, 2007, 10(5): 692-697.
[3] 李雪妍. 融合指纹和指静脉的多模态生物识别技术的研究[D].吉林: 吉林大学, 2008.
LI Xue-yan. Study of multibiometrics system based on fingerprint and finger vein[D]. Jilin: Jilin University, 2008.
[4] 钱晓华. 手指静脉识别算法[D]. 吉林: 吉林大学, 2009.
QIANG Xiao-hua. Research of finger-vein recognition algorithm[D]. Jilin: Jilin University, 2009.
[5] Daugman J. Complete discrete 2D gabor transforms by neural networks for image analysis and compression[J]. IEEE Transactions on Acoustic, Speech and Signal Processing, 1988, 7(36): 1169-1179.
[6] Wu X, Zhang D, Wang K. Fusion of phase and orientation information for palmprint authen-tication[J]. Pattern Analysis and Application, 2005, 2: 29-32.
[7] Daugman J. How iris recognition works[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2004, 14(1): 21-30.
[8] Daugman J. High confidence visual recognition of persons by a test of statistical independence[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1993, 15(11): 1148-1161.
[9] Watanabe M, Hamamoto Y, Yasuda T, et al. Normalization techniques of handwritten numerals for gabor filters[C]//Fourth International Conference Document Analysis and Recognition (ICDAR’97). Ulm, Germany: August 18-20.
(编辑 杨华)
收稿日期:2011-04-15;修回日期:2011-06-15
基金项目:国家“863”计划资助项目(2008AA01Z148);博士点专项科研基金资助项目(20102304110004)
通信作者:王科俊(1962-),男,吉林省吉林人,教授,博士生导师,从事生物特征识别与智能监控、神经网络、计算生物信息学等研究;电话:13936459728;E-mail:heukjun@sohu.com