J. Cent. South Univ. Technol. (2008) 15(s1): 271-274

DOI: 10.1007/s11771-008-361-8

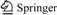
Damping of magnetorheological elastomers

CHEN Lin(陈 琳)^{1, 2}, GONG Xing-long(龚兴龙)^{1, 2}

(1. CAS Key Laboratory of Mechanical Behavior and Design of Materials,

University of Science and Technology of China, Hefei 230027, China;

2. Department of Modern Mechanics, University of Science and Technology of China, Hefei 230027, China)

Abstract: The damping property of magnetorheological elastomers (MREs) is characterized by a modified dynamic mechanical-magnetic coupled analyzer. The influence of external magnetic flux density, damping of matrix, content of iron particles, dynamic strain and driving frequency on the MREs’ damping was investigated experimentally. The results indicate that the MREs’ damping property depends on the interfacial slip between the inner particles and the matrix. Different from the general composite materials, the interfacial slip in MRE is affected by the external applied magnetic field.

Key words: magnetorheological elastomers; damping property; interfacial slip

1 Introduction

Magnetorheological elastomer (MRE) is a class of smart material whose rheological and mechanical properties can be reversibly and rapidly controlled by an external magnetic field^[1-3]. This is achieved via adding the micro-sized magnetizable particles into the elastomers or rubber-like materials. When such mixture is exposed to a magnetic field before curing, the field-induced interactions between particles can result in the formation of anisotropic ordered pre-configuration. such as chains or more complex three-dimensional structures. After the mixture is cured or crosslinked, these structures are locked into place. When such prepared MREs are exposed to an applied magnetic field, the field-induced dipole magnetic forces between the particles result in the field dependence performance. MREs have attracted increasing attention and obtained broad application prospects recently. BELLAN et al^[4] studied the shear stress—strain relationship under applied magnetic fields. GINDER et al^[5] investigated the magnetostriction performance. And BOSSIS et al^[6] researched on the conductivity and optical properties. GINDER^[7], LERNER^[8] and DENG^[9] developed adaptive tuned vibration absorbers respectively. However, little work has focused on the damping property of the MRE. Furthermore, the absorber effect of those MREs based vibration absorbers greatly depends on the MREs’ damping property^[10].

This paper aims to research the damping property of MRE. The influence of the matrix type, content of iron particles, dynamic strain amplitude and driving frequency are characterized by using a modified dynamic mechanical analyzer (DMA) system.

2 Experimental

2.1 Preparation of MRE materials

Two groups of MRE samples were prepared.

The first group samples were fabricated on the different types of matrix, including silicon rubber (SiR), natural rubber (NR) and chloroprene rubber (CIIR). These samples had the same ingredient proportions by mass (30% of rubber matrix, 10% of plasticizers, and 60% of iron particles). The iron particles were provided by BASF (German, model of SM) and with the average diameter of 2.5 μm.

When preparing the MRE samples based on SR, the iron particles, dimethyl-silicon oil (act as plasticizers, with the viscosity of 0.3 Pa?s, provided by Shanghai Resin Factory, China) and RTV SiR (Xida Adhesives Factory, China, Model 704) were mixed together, then the mixture was put into the mold under the magnetic flux density of 0.4 T, for curing up for 24 h at room temperature. When preparing the MRE samples based on NR and CIIR, the fabrication progress consisted of three major steps: mixing, forming pre-configuration and sulfuration. During fabrication, each composition was firstly mixed homogeneously, then the magnetic particles formed the order structures and finally the sample became an elastomer. The illumination of the mechanical-magnetic coupling fabrication system was detailed in Ref.[11]. With this method, MRE samples based on NR and CIIR were prepared under the external magnetic flux densities of 0.4 T. The NR, CIIR and other additives were provided by Hefei Wangyou Rubber Company of China.

The second group samples were based on NR, with different contents of iron particles, including 60%, 70%, 80% and 90% (mass fraction). In each sample, the content of the rubber matrix and plasticizers were the same, and the pre-configuration magnetic flux density was set at 1.0 T.

2.2 Dynamic testing system of MRE performance

A dynamic mechanical analyzer (DMA) is the common equipment for dynamic testing on viscoelastic material. In this work, the DMA (Triton Technology Ltd.UK, Model Tritec 2 000 B) system was modified to characterize MRE performances by introducing a self-made electromagnet which can generate a variable magnetic flux density up to 1.0 T (sketch map shown in Fig.1). This system applies a fixed oscillatory strain to the specimen and measures the amplitude and phase of the output force, from which stress, modulus (including shear storage modulus G′ and loss modulus G″ included) and the loss tangent(tan δ=G″/G′) can be calculated. So the damping ratio of MRE samples is obtained. Testing involved recording the modulus and the damping ratio of various specimens at various frequencies, strains and applied magnetic fields.

The experiment was started at the room temperature, and the increment of temperature of the electromagnet was less than 3 ℃ during the stage of the whole experiment.

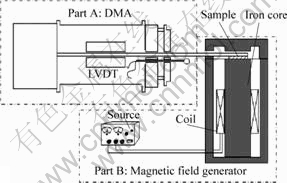
Fig.1 Sketch map of magnet-mechanics coupled DMA

3 Results and discussion

3.1 Damping ratio of MREs with different matrix types

The damping ratio of the first group MRE samples, based on the NR, SiR and CIIR respectively, was measured at dynamic strain of 0.3%, driving frequency of 5 Hz, and under various magnetic flux densities (B) from 0 up to 800 mT, and the results are shown in Fig.2. It can be seen from this figure, the damping ratio of the MRE based on NR is lower than that of MRE based on SiR and CIIR. The damping ratio of the composite consists of two parts: damping ratio of the matrix and the energy dissipation between the reinforcement and the matrix. It has been proved in the rubber technology that the damping ratio of NR is lower than that of SiR and CIIR^[12]. So, if the other conditions are the same, the lower damping ratio of matrix will result in the lower damping ratio of MRE samples.

It is also shown in Fig.2 that with increasing magnetic field, the damping ratios of the MRE samples follow an increasing trend until a maximum value (at about B=300 mT) then a decreasing trend later. This result has not been reported somewhere so far. It can be explained by the energy dissipation method. The energy dissipation of the materials mainly comes from the interaction among different inner phases^[13]. The energy dissipation on the interface is a key factor on the interaction, and depends on the interaction force multiplied by the slipping displacement. When a low magnetic field is applied to the MRE sample, the magnetic force between magnetic particles occurs and transfers to the matrix. Then the interaction force between the particles and the matrix is enhanced. In this condition, more energy is dissipated on the interface slipping. So MRE sample’s damping ratio is macroscopically increased by the magnetic field. It is also noted that the slipping displacement is influenced by the interaction force. When a high magnetic field is applied to the MRE sample, the strong interaction force between the particles and the matrix decreases the slipping displacement. Then the energy dissipation is reduced and the damping ratio is decreased when the magnetic field further increases.

Fig.2 Damping ratio of MREs based on different types of matrix

3.2 Damping ratio of MREs with different content of iron particles

The damping ratios of the second group MRE samples, whose iron particle contents are 60%, 70%, 80% and 90% respectively, were measured at dynamic strain of 0.30%, driving frequency of 5 Hz, and under various magnetic fields from 0 up to 800 mT, and the results are shown in Fig.3. It can be seen from this figure, the damping ratio of MRE decreases with the increment of the iron particle contents. As the particle contents increase, the numbers of the contact points between particles and the matrix increase. More energy is dissipated from the slipping on the interface, and the damping ratio increases accordingly.

3.3 Damping ratio of MRE applied with different dynamic strain amplitudes

The MRE sample based on NR prepared in the first group was measured at driving frequency of 5 Hz, under various magnetic fields from 0 up to 800 mT, and at dynamic strain amplitude of 0.03%, 0.16%, 0.30% and 0.50% respectively, and the results are shown in Fig.4. It can be seen from this figure, the damping ratio has great dependence on the dynamic strain amplitude. When the strain amplitude is 0.03%, the average damping ratio is 0.04; when the strain amplitude is 0.50%, the average damping ratio reaches 0.11. This result also can be explained by the energy dissipation method. As the dynamic strain amplitude increases, the slipping displacement on the interface is increased. Then more energy will be dissipated, and the damping ratio  increases accordingly. The figure also shows that little change happens for the damp ratio by increasing the strain amplitude to 0.30%. It is indicated that the slipping displacement on the interface almost reaches the maximum when the dynamic strain amplitude is 0.30%.

Fig.3 Damping ratios of MREs with different iron particle contents

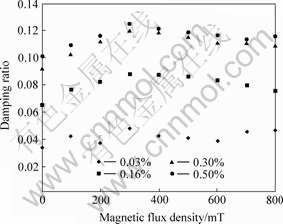
Fig.4 Damping ratios of MREs measured under different dynamic strain amplitudes

3.4 Damping ratio of MRE applied with different driving frequencies

The MRE sample based on NR fabricated in the first group was measured at dynamic strain amplitude of 0.30%, under various magnetic fields from 0 up to 800 mT, and at driving frequency of 5, 10, 15 and 20 Hz respectively, and the results are shown in Fig.5. In the figure, the damping ratio measured at 5 Hz, is lower than measured at other frequencies when the magnetic flux density is zero, higher than others when the magnetic flux density is 300 mT, and lower than others when the magnetic flux density is 800 mT. So the damping ratio at 5 Hz changes faster than others in applied field. It is indicated that the magnetic field has more influence on the damping ratio when the MRE sample is driven at lower frequency.

Fig.5 Damping ratios of MREs measured at different driving frequencies

4 Conclusions

The damping property of MRE sample was experimentally explored. Main results are summarized below.

1) The critical magnetic flux density for MRE damping ratio is at 300 mT. With increasing magnetic field, the damping ratios increase firstly and decrease after reaching the critical value.

2) The damping ratio of MRE is affected by that of the matrix. Low damping ratio of matrix leads to low damping ratio of MRE.

3) As the iron particle contents increase, the numbers of the contact points between particles and the matrix increase. Then more energy is dissipated from the slipping on the interface, and the damping ratio increases accordingly.

4) The dynamic strain amplitude plays an important role on the damping ratio of MRE. As the dynamic strain amplitude increases, the slipping displacement on the interface increases. Then the damping ratio increases accordingly.

5) At lower driving frequency, the damping ratio of MRE sample has more dependence on the magnetic flux density.

References

[1] SHIGA T, OKADA A, KURAUCHI T. Magnetro-viscoelastic behavior of composite gels[J]. J Appl Polym Sci, 1995, 58: 787-792.

[2] CARLSON J D, JOLLY M R. MR fluid, foam and elastomer devices[J]. Mechatronics, 2000, 10: 555-569.

[3] GINDER J M, NICHOLS M E, ELIE L D, TARDIFF J L. Magnetorheological elastomers: Properties and applications[C]// The Proceedings of the Society of Photo-Optical Instrumentation Engineers. 1999: 131-138.

[4] BELLAN C, BOSSIS G. Field dependence of viscoelastic properties of MR elastomers[J]. Int J Mod Phys B, 2002, 16: 2447-2453.

[5] GINDER J M, CLARK S M. Magnetostrictive phenomena in magnetorheological elastomers[C]// The Proceedings of the 8th International Conference on ER Fluids and MR Suspensions. 2002: 472-478.

[6] BOSSIS G, ABBO C, CUTILLAS S, LACIS S, ME?TAYER C. Electroactive and electrostructured elastomers[J]. Int J Mod Phys B, 2001, 15(6/7): 564-573.

[7] GINDER J M, SCHLOTTER W F, NICHOLS M E. Magnetorheological elastomers in tunable vibration absorbers[C]// Proceedings of SPIE. 2001: 103-110.

[8] LERNER A A, CUNEFARE K A. US Patent, 20050040922[P].

[9] DENG H X, GONG X L, WANG L H. Development of an adaptive tuned vibration absorber with magnetorheological elastomer[J]. Smart Mater Struct, 2006, 15: N111-N16.

[10] SUN H L, ZHANG P Q, GONG X L, CHEN H B. A novel kind of active resonator absorber and the simulation on its control effort[J]. J Sound Vib, 2007, 300: 117-125.

[11] CHEN L, GONG X L, JIANG W Q, YAO J J, DENG H X, LI W H. Investigation on magnetorheological elastomers based on natural rubber[J]. J Mater Sci, 2007, 42: 5483-5489.

[12] CHANDRA R, SINGH S P, GUPTA K. Damping studies in fiber-reinforced composites—A review[J]. Compos Struct, 1999,46: 41-51.

(Edited by CHEN Ai-hua)

Foundation item: Project(10672154) supported by the National Natural Science Foundation of China; Project(20050358010) supported by the SRFDP of China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: GONG Xing-long, Professor; Tel: +86-551-3600419; E-mail: gongxl@ustc.edu.cn