路基砂土液化势的灰色三角白化权函数聚类方法
禹建兵1,刘浪2
(中南大学 资源与安全工程学院,湖南 长沙,410083)
摘要:借鉴灰色系统理论,将砂土液化与其影响因素之间的关系作为灰色系统,提出采用灰类白化权函数聚类的预测方法对砂土液化势进行预测。分析影响砂土液化的因素,选取震级M、地面加速度最大值gmax、标准贯入击数N63.5、比贯入阻力ps、相对密实度Dr、平均粒径D50和地下水位dw这7个实测指标作为砂土液化势预测的主要影响因子,并构造适于砂土液化势预测的各聚类指标的白化权函数,同时引入信息熵理论确定各指标的权重,采用本文提出的方法对16组唐山大地震震害资料对模型进行评价,利用广东省三水市部分地区的9组砂土液化实例进行仿真测试,并与工程实际结果进行对比。研究结果表明:所提出的基于灰类白化权函数聚类的砂土液化势预测方法具有较高的预测精度,准确率达90%。
关键词:砂土液化;预测;灰色聚类;白化权函数
中图分类号:TU449 文献标志码:A 文章编号:1672-7207(2014)01-0269-07
Sand liquefaction in road subgrade prediction method based on grey whitenization weight function cluster theory
YU Jianbin1, LIU Lang2
(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)
Abstract: Based on gray system theory, and taking the relationship between the lique faction and its influence factors as gray system, a method to predict liquefaction potential of sand was established using grey whitenization weight function cluster theory. Seven parameters including earthquake magnitude M, peak ground surface acceleration gmax, standard penetration N63.5, specific penetration resistance ps, relative compaction Dr, average particle diameter D50, and groundwater table dw were used as influencing factors of sand liquefaction potential measured indicators and to construct the clustering index whitening weight function to forecast the potential of liquefaction. The information entropy theory was introduced to determine the weight of each index, the proposed method was used to evaluate the model using 16 groups of Tangshan earthquake seismic damage data, and the simulation test was made for nine groups of soil liquefactionin Sanshui City, Guangdong Province, and the comparison was made. The results show that the proposed method to predict sand liquefaction potential has high prediction accuracy based on class whitening weight function clustering gray, and the accuracy rate is 90%, which can promote the actual project.
Key words: sand liquefaction; prediction; grey cluster; whitening weight function
砂土液化是指饱和松散砂土或黏聚力较弱的轻亚黏土在地震作用下产生急剧的状态改变和强度丧失,表现出类似液体性状的现象[1]。它具有很大的危害性,常表现为喷水冒砂、地面沉陷或坍塌、诱发高速滑坡或地基失稳等现象。因此,砂土地震液化评判一直是地震工程、岩土工程以及自然灾害防治工程的一项重要基础性研究工作。自1964年美国阿拉斯加和日本新泻地震以来,国内外学者在砂土液化判别方面进行了大量的研究工作[1-4],已提出经验公式法、Seed简化分析法、临界加速度判别法、规范法、概率与统计方法、动力反应分析方法等多种砂土液化判别方法。目前,评判砂土液化广泛使用的动剪应力法和规范法等确定性方法都是基于经验和室内试验建立的,用平均值来描述液化等级风险,将导致结果不准确,引入概率统计理论能克服这一缺陷,但该法因模型构建假设、系统误差和信息不完整,所求的砂土液化概率跟实际场地液化情况仍有差别。近年来,国内外学者对此进行了许多研究[5-14],神经网络预测方法[5-8]、模糊综合评判法[9]、可靠性分析[10-11]、可拓学[12]、支持向量机[12-13]、距离判别法[14]、盲数理论[15]等先进的计算理论与方法逐步引入到砂土液化势评价中。上述方法有其自身的特点,同时也存在一定的局限性,如:人工神经网络方法存在收敛速度慢,隐含层确定具有主观性等弱点;模糊综合评判法常要对各指标赋予不同的权重,会带有一定的主观性和随意性;距离判别法未考虑各样本先验概率及各指标权重;支持向量机方法的参数合理确定并非易事等。此外,这些砂土评价模型都只进行了砂土液化是否可能的识别,没有对液化危害等级进行划分,且影响砂土液化的因素具有复杂性、多样性和非线性的特点,很难提出准确、通用的判别准则,如何建立一种多参数综合评价模型对砂土液化进行正确预测及抗震减灾具有重要意义。1982 年邓聚龙创立的灰色系统理论提供了一条崭新的途径,它以“部分信息已知、部分信息未知”的小样本和贫信息不确定系统为研究对象,主要通过对“部分”已知信息的生成、开发提取有价值的信息,实现对系统运行规律的正确描述和有效控制[16-18]。灰色聚类分析应用灰色系统理论的思想、方法进行分析,根据关联矩阵或灰数的白化权函数将一些观测指标或对象聚集成若干个可定义类别[17-18],而评价砂土地震液化等级对象具有随机性和模糊性以及不同条件下的可变性,故砂土地震液化等级评价问题实质上是一个不相容问题。岩爆是内外因多因素综合作用的结果,具有模糊性,复杂性和不确定性,其影响因素目前没有统一标准,部分明确指标的具体量值也难以确定,而是一个变化的灰区间,各因素对砂土液化的影响程度也是一种灰关系。为此,本文作者在前人研究工作的基础上,借鉴灰色聚类评估的理论和思想,将砂土液化与其影响因素之间的关系看成一种灰色系统,将灰色理论运用到路基砂土液化分级评价中,同时引入信息熵理论[19-20]确定各指标的权重,以较好消除人为因素带来的偏差,使评价结果更符合实际,从而为工程的设计与施工提供合理的决策依据。
1 基于中心点三角白化权函数的灰熵评估原理
灰色聚类评估法是根据若干指标将一些研究对象进行分类的方法,可分为灰色关联聚类和灰色白化权函数聚类。灰色关联聚类主要用于同类因素的归并,以使复杂系统简化;灰色白化权函数聚类是以灰数的白化权函数生成为基础,它将收集到的分散信息按照灰类进行归纳,主要用于检查观测对象是否属于事先设定的不同类别,以便区别对待。当评估指标意义不同、量纲不同且在数值上差别很大时,一般采用基于三角白化权函数的灰色评估[16],其步骤如下。
1.1 确定灰色聚类区间
设有n个聚类对象,m个聚类指标,t个不同的灰类,聚类对象i关于聚类指标j的量化值为xij(i=1, 2, …, n; j=1, 2, …, m)。fkj(xij)为聚类指标j关于k(k =1, 2, …, t)灰类的白化权函数。按照评估要求所需划分灰类数t,将各个指标的取值范围也相应地划分为t个灰类,分别以ξ1, ξ2, …, ξt作为各个灰类的节点,将灰类向不同方向进行拓展,考虑增加0灰类和t+1灰类,并确定其中心点ξ0和 ξt+1,得到新的中心点序列ξ0, ξ1, …, ξt, ξt+1。
1.2 确定各灰类的三角白化权函数
白化权函数可以定量描述某一评估对象隶属于某个灰类的程度。在划分灰类时,将属于某灰类程度最大的点作为中心点,以分段函数表示路基砂土液化势评价指标的白化权函数,用以描述某项评价指标的灰数对其阀值的接近程度。基于中心点的灰类三角白化权函数步骤如下[14, 16]。
(1) 按照评估要求所需划分的灰类数t,将各个指标的取值范围也相应地划分为t个灰类。如将j指标的取值范围[ξ1, ξt+1]划分为t个区间[ξ1, ξ2],…,[ξk-1, ξk],…,[ξs-1, ξs],[ξs, ξs+1]。其中,ξk(k=1, 2, …, t, t+l)一般根据实际情况的要求或定性研究结果确定。
(2) 令ξk =(ξk-1+ξk+1)/2属于第 k个灰类的白化权函数值为1,连接(ξk, 1)与第k-1个灰类的起点ξk-1,和第k+1个灰类的终点ξk+1,得到j指标关于k灰类的三角白化权函数fjk (j=1, 2, …, m; k=1, 2, …, t),见图1。
对于指标j的1 个观测值x,可由下式计算其属于灰类k (k=1, 2, …, t) 的隶属度 :
:
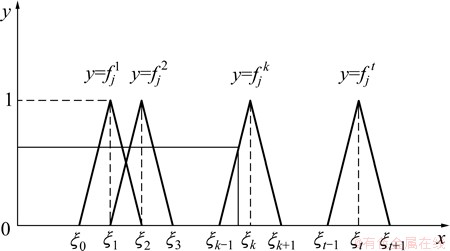
图1 中心点三角白化权函数示意图
Fig. 1 Schematic diagram of center triangle whitening weight function
 (1)
(1)
1.3 用熵权确定各指标权重
在确定评价指标的权重时,一般采用Delphi法、AHP法、两两比较法、环比评分法等主观赋权法,可能造成评价结果因人的主观因素而形成偏差,破坏评估的客观性和规范性。在信息论中,熵[17-18]既可用来度量系统无序程度,还可用来度量数据本身所提供信息的有效性,故可用信息熵评价所获系统信息的有序度及其效用,即由评价指标值构成的判断矩阵来确定指标权重,它可尽量消除各指标权重计算的人为干扰,使评价结果更符合实际。设wj表示测量指标 与其他指标相比具有的相对重要度,要求满足:
与其他指标相比具有的相对重要度,要求满足: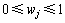 ,
,
且 。称wj为
。称wj为 的权重,w={w1, w2, …, wm}为指标权重向量,根据熵确定权重,即
的权重,w={w1, w2, …, wm}为指标权重向量,根据熵确定权重,即
 (2)
(2)
显然,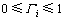 。令
。令
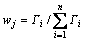 (3)
(3)
由式(2)和(3)求得wj,进而求得权重向量w。
1.4 砂土液化势等级判别
计算对象 i (i=1, 2, …, n)关于灰类 k (k=1, 2, …, t)的综合聚类系数 :
:
 (4)
(4)
式中: 为对象i在指标j下属于k灰类的白化权函数;wj为指标j在综合聚类中的权重,可由熵权计算。
为对象i在指标j下属于k灰类的白化权函数;wj为指标j在综合聚类中的权重,可由熵权计算。
由 判断出对象i属于灰类k*。若多个对象同属于灰类k*,则需进一步根据综合聚类系数确定同属于灰类k*各对象的位次。
判断出对象i属于灰类k*。若多个对象同属于灰类k*,则需进一步根据综合聚类系数确定同属于灰类k*各对象的位次。
2 砂土液化的灰熵聚类预测方法
2.1 砂土地震液化的主要影响因子
砂土液化的发生、发展是一个复杂的过程,其影响因素很多,随机性大,且各因素之间呈高度的非线性。参考有关砂土液化评判指标体系研究,大体可分为 3 类[7-8, 11-12]:(1) 砂土自身特性,如土的种类、颗粒组成、密实度等;(2) 土层埋深与地下水位;(3) 动荷条件,如地震烈度、持续时间等。建立路基砂土液化的灰熵评估模型时,还需考虑分析资料的易获性和代表性,选取震级M、地面加速度最大值gmax、标准贯入击数N63.5、比贯入阻力ps、相对密实度Dr、平均粒径D50、地下水位dw这7个特征参数指标作为灰熵评估指标,其分级判据指标如表1所示[11]。在确定评数据格式为:下限值~上限值(中心点)。
表1 砂土液化势的评价指标及分级标准
Table 1 Evaluation and grading standards for sand liquefaction potential
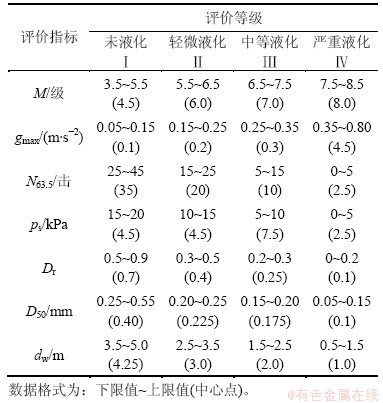
价等级分类方案时,根据部分学者研究成果并参考行业规范,将砂土液化势分为未液化(Ⅰ)、轻微液化(Ⅱ)、中等液化(Ⅲ)和严重液化(Ⅳ) 这4个等级,分级标准描述见表2 [11]。
2.2 建立路基砂土液化势的灰熵评估模型
为了验证本文提出的基于灰类白化权函数聚类的砂土液化势评价方法的有效性和实用性,从唐山大地震震害的文献资料中搜集整理了16组数据作为灰熵评估模型的训练样本。在这些数据中,未液化(Ⅰ)、轻微液化(Ⅱ)、中等液化(Ⅲ)和严重液化(Ⅳ)的情况各占4组数据,具体的液化结果见表3[7-8, 19]。在评价过程中,首先将需要评估的砂土液化样本作为一个聚类对象,然后,根据灰色聚类理论对表1原始区间灰数序列进行拓展,构建基于中心点的三角白化权函数,其白化权函数如图2所示。为方便陈述,以表1中样本Ⅰ为例。根据该样本特征值并运用式(1)计算出聚类对象i属于k灰类的聚类系数 根据表3中7个评价因子的取值,分别代入图2(a)~(g)的三角白化权函数中,计算可知样本1 的各白化权函数值,见表4。利用信息熵理论确定各指标权重,据式(2)和(3)可得评价指标的权重向量w={0.15, 0.09, 0.15, 0.17, 0.13, 0.14, 0.17}。求得灰色聚类系数向量为(0.487, 0.285, 0.141, 0),根据上文中判别准则可知样本1的液化势等级属于灰类K1,即未液化(Ⅰ)。
表2 砂土液化势等级划分标准
Table 2 Rank division standard for sand liquefaction potential

表3 砂土液化样本评价指标及液化实际结果
Table 3 Parameters of seepage property for sandstone
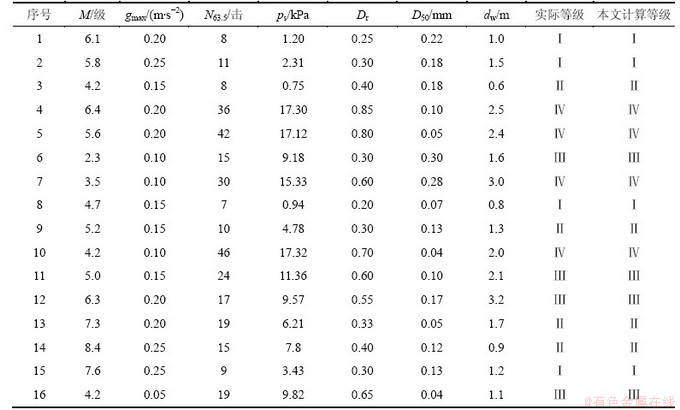
表4 样本1的三角白化权函数值
Table 4 Sample 1 of triangle whitening weight function value


图2 不同砂土液化势评价指标的三角白化权函数图
Fig. 2 Triangle whitening weight function of different sand liquefaction potential influence factors
2.3 评价结果分析
同理可对样本2~16进行逐一评价,其唐山大地震中部分实例的原始数据、砂土液化灰色聚类预测结果和实际情况对比见表5。从表5可以看出:16个砂土液化评价样本灰熵评价结果与实际情况基本吻合,从而说明本文砂土液化评价模型的有效性和可行性。可见:将灰熵分析模型应用于砂土液化等级评价的判定中完全可行、高效可靠的,具有较高的实用价值。用灰色聚类法对砂土液化势进行分类,使其分类数学化与定量化,对于解决常规多因子分类中由于指标交叉而不能归类的问题更具优越性。首先,将各个样本的测试值分别与砂土液化标准的不同级别进行比较,不同的评价因子处于不同的级别区间,选择级别最低的级别作为该样本的评价级别;将级别最低的样本的评价因子分别代入相应的该级别的三角白化权函数中,计算其白化值,白化值最高的评价因子判定为首要液化势;将该测点的评价因子的白化值相加,即为该测点对该级别隶属度。同理,将处于同一级别的不同测点的隶属度分别计算,最后进行比较,即可判断出各样本液化势。依次计算高一级别的各测点的隶属度并进行比较,最后判定出所有样本的砂土液化的趋势。
2.4 工程运用
工程实例采用文献[7,8,20]中广东三水资料(表7)验证本文提出模型的可行性和有效性。三水市位于珠江三角洲,洲内第四系沉积物下部为晚更新世陆相砂砾层,厚为3~5 m;中部为早—中全新世海相淤泥层,厚为15~20 m,最厚达40.28 m;上部为晚全新世平原相砂质黏土层,厚度为3~5 m。本区地震烈度为Ⅶ度,淤泥和饱和的粉细砂在振动荷载下会产生液化。将评价结果与有关文献提供的砂土液化情况及评判结果进行对比分析。利用本文方法预测的砂土液化等级结果见表6,与人工神经网络模型(ANN)[8]的预测结果比较结果表明,2种方法所得结果一致,进一步表明三角白化权灰熵模型在砂土液化分级预测中的有效性与可行性。
表5 灰色聚类系数向量
Table 5 Parameters of seepage property for sandstone
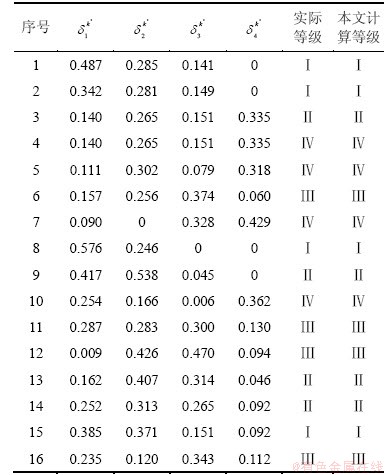
表6 广东三水砂土液化测试样本评价指标及评价结果对比
Table 6 Guangdong Sanshui test samples of soil liquefaction evaluation index value and comparison of evaluation results

3 结论
(1) 针对砂土液化势评价与其影响因素间的非常复杂的非线性关系,引入灰色聚类思想,选取震级M、地面加速度最大值gmax、标准贯入击数N63.5、比贯入阻力ps、相对密实度Dr、平均粒径D50、地下水位dw等7个特征参数指标,建立基于中心点的三角白化权函数砂土液化灰色评价模型。
(2) 在评价过程中,将信息熵理论和灰色聚类理论耦合到一个评价模型中,利用熵权确定权重的方法更符合客观实际,可提高路基砂土液化势等级评价模型结果的精度。充分利用评价样本信息本身来判别液化等级,在一定程度上减少了人为的主观因素对判别结果的影响,使评价结果更加准确、可信。
(3) 本文所建立的砂土液化势等级评价的三角白化权灰熵模型,计算方法简单,评价结果与实际结果较吻合,为砂土液化势评价方法提供了一种新途径。
(4) 砂土液化势灰熵评价结论的准确性与可信度取决于所采用的评价指标及如何构造灰类白化权函数。为此,需深入了解砂土液化本质,分析各影响因素对砂土液化的影响,构造更加广泛适用的灰类白化函数,以进一步提高路基砂土液化势评估模型的可靠性。
参考文献:
[1] 宫继昌, 王宁, 葛明明, 等. 砂土液化判别的研究现状及存在问题[J]. 吉林建筑工程学院学报, 2010, 27(3): 13-16.
GONG Jichang, WANG Ning, GE Mingming, et al. Sand liquefaction evaluation research and exiting problems[J]. Journal of Jilin Institute of Architecture & Civil Engineering, 2010, 27(3): 13-16.
[2] Seed H B, Idriss I M. Simplified procedure for evaluating soil liquefaction potential[J]. Journal of Geotechnical Engineering, 1971, 97(9): 1249-1273.
[3] GB 50011—2001,建筑抗震设计规范[S].
GB 50011—2001, Code for seismic design of buildings[S].
[4] Juang C H, Chen C J, Tien Y M. Appraising cone penetration test based liquefaction resistance evaluation methods: Artificial neural network approach[J]. Canadian Geotechnical Journal, 1999, 36(3): 443-454.
[5] 刘红军, 薛新华. 砂土地震液化预测的人工神经网络模型[J]. 岩土力学, 2004, 25(12): 1942-1946.
LIU Hongjun, XUE Xinhua. Artificial neural network model for prediction of seismic liquefaction of sand soil[J]. Rock and Soil Mechanics, 2004, 25(12): 1942-1946.
[6] 陈国兴, 李方明. 基于径向基函数神经网络模型的砂土液化概率判别方法[J]. 岩土工程学报, 2006, 28(3): 301-305.
CHEN Guoxing, LI Fangming. Probabilistic estimation of sand liquefaction based on neural network model of radial basis function[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 301-305.
[7] 董贤哲. 基于补偿模糊神经网络的砂土液化势评价研究[D]. 北京: 中国地质大学工程技术学院, 2005: 27-35.
DONG Xianzhe. Research on assessment of sand liquefaction potential based on compensative fuzzy neural network[D]. Beijing: China University of Geosciences. School of Engineering and Technology, 2005: 27-35.
[8] 安宁. 路基砂土液化等级的BP网络预测研究[J]. 土工基础, 2007, 21(4): 45-48.
AN Ning. Pre-determination of sand liquefaction in road subgrade by BP network[J]. Soil Eng and Foundation, 2007, 21(4): 45-48.
[9] 翁焕学. 砂土地震液化模糊综合评判实用方法[J]. 岩土工程学报, 1993, 15(2): 74-79.
WENG Huanxue. Saturated sand liquefaction potential estimation method based on fuzzy comprehensive evaluation[J]. Chinese Journal Geotechnical Engineering, 1993, 15(2): 74-79.
[10] Juang C H, Rosowsky D V, Tang W H. Reliability-based method for assessing liquefaction potential of soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(8): 684-689.
[11] 汪明武, 罗国煜. 可靠性分析在砂土液化势评价中的应用[J]. 岩土工程学报, 2000, 22(5): 542-544.
WANG Mingwu, LUO Guoyu. Application of reliability analysis to assessment of sand liquefaction potential[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(5): 542-544.
[12] 陈荣淋. 基于可拓学和支持向量机理论的砂土液化势综合评价研究[D]. 厦门: 华侨大学土木工程学院, 2006: 10-30.
CHEN Ronglin. Research on assessment of sand liquefaction potential based on extenics and support vector machine[D]. Xiamen: Huaqiao University. School of Civil Engineering, 2006: 10-30.
[13] Pal M. Support vector machines-based modelling of seismic liquefaction potential[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30: 983-996.
[14] 金志仁. 距离判别分析方法的砂土液化预测模型及应用[J]. 岩土工程学报, 2008, 30(5): 776-780.
JIN Zhiren. Prediction of sand liquefaction based on discriminant analysis and its application[J]. Chinese Journal Geotechnical Engineering, 2008, 30(5): 776-780.
[15] 汪明武, 李丽, 金菊良. 基于盲数理论的液化等级风险评价模型[J]. 岩土工程学报, 2010, 32(2): 303-307.
WANG Mingwu, LI Li, JIN Juliang. Application of unascertained number theory to risk evaluation of liquefaction grade[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(2): 303-307.
[16] 邓聚龙. 灰理论基础[M]. 武汉: 华中科技大学出版社, 2002: 33-41.
DENG Julong. Grey theory[M]. Wuhan: Huazhong University of Science and Technology Press, 2002: 33-41.
[17] 谢学斌, 潘长良. 岩爆灾害的灰类白化权函数聚类预测方法[J]. 湖南大学学报(自然科学版), 2007, 34(8): 16-20.
XIE Xuebin, PAN Changliang. Rockburst prediction method based on grey whitenization weight function cluster theory[J]. Journal of Hunan University (Natural Sciences), 2007, 34(8): 16-20.
[18] 刘思峰, 党耀国, 方志耕, 等. 灰色系统理论及其应用[M]. 5版. 北京: 科学出版社, 2010: 72-84.
LIU Sifeng, DANG Yaoguo, FANG Zhigang, et al. Grey system theory and its application[M]. 5rd ed. Beijing: Science Press, 2010: 72-84.
[19] 薛剑光, 周健, 史秀志, 等. 基于熵权属性识别模型的岩体可爆性分级评价[J]. 中南大学学报(自然科学版), 2010, 41(1): 251-256.
XUE Jianguang, ZHOU Jian, SHI Xiuzhi, et al. Assessment of classification for rock mass blastability based on entropy coefficient of attribute recognition model[J]. Journal of Central South University (Science and Technology), 2010, 41(1): 251-256.
[20] Jaynes E T. Information theory and statistical mechanics[J]. Physical Review, 1957(106): 620-630.
(编辑 陈灿华)
收稿日期:2012-12-11;修回日期:2013-03-02
基金项目:国家自然科学基金资助项目(50774092);全国优秀博士学位论文专项资金资助项目(200449)
通信作者:禹建兵(1973-),男,湖南双峰人,博士研究生,副教授,高级工程师,从事土木工程施工工艺研究;电话:13908475168;E-mail: 1255875562@qq.com