瑞雷波数值模拟中的数值频散校正策略及实例分析

丰赟^{1, 2}，周竹生¹，沙椿²

(1. 中南大学 地球科学与信息物理学院，湖南 长沙，410083；

(2. 四川中水成勘院 工程勘察有限责任公司，四川 成都，610072)

摘要：为寻求快速、高精度的瑞雷波数值模拟方法，将常用于流体动力学中的通量校正传输技术(FCT)与交错网格有限差分方法相结合，对浅层各向同性弹性介质进行包括瑞雷面波和体波在内的全波场模拟。模拟结果表明：该方法有效地压制了粗网格条件下的数值频散现象，并保留了真实的波场振荡，特别是层状介质中瑞雷波的频散特征被凸显；在同一精度下，该方法与细化网格方法相比，计算效率提高1.3倍。

关键词：瑞雷波；数值模拟；有限差分法；交错网格；数值频散；FCT

中图分类号：P631          文献标志码：A         文章编号：1672-7207(2012)06-2231-07

Numerical dispersion correction method and cases analysis in numerical modeling of Rayleigh surface wave

FENG Yun^{1, 2}, ZHOU Zhu-sheng¹, SHA Chun²

(1. School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;

2. Sichuan Hydropower Engineering Investigation Co. Ltd., Chengdu 610072, China)

Abstract: In order to seek a fast and effective method for wave-field simulation, the flux-corrected transport method which was commonly used in fluid dynamics and the staggered-grid finite difference method were combined, and the whole wave field including Rayleigh surface wave and body wave were simulated by FCT finite difference method. The results show that this method is effective to suppress the numerical frequency dispersion phenomenon by thick grids, but retain the real wave oscillation, and especially the dispersion characteristics of Rayleigh surface wave in the layered mediums can be highlighted. Compared with the thinning grids method, it raises the computing speed by 1.3 times to suppress the dispersion.

Key words: Rayleigh surface wave; numerical modeling; finite-difference method; staggered-grids; numerical dispersion; flux-corrected transport

瑞雷波勘探作为一种新物探方法，近年来发展迅速，其具有经济、快捷、高效的特点，被广泛应用于工程地质勘察和工程无损检测。目前，人们对瑞雷波的理论研究主要集中在频散曲线的正演和反演方面。为更准确、全面地了解瑞雷波的传播特性，近年来，人们对基于波动方程的瑞雷波数值模拟进行了研究，如：周竹生等^[1]采用交错网格有限差分法对水平层状各向同性弹性介质进行了全波场模拟，并对瑞雷波的传播特征进行了探讨，取得了较好的模拟效果，但差分精度较低导致模拟的波场出现了较明显的数值频散现象；Xu等^[2]在模拟中采用AEA法对自由边界进行处理，由于采用空间二阶差分精度，为满足精度要求，必须减小网格间距以增加最小波长中的网格数，导致计算量增加；Bohlen^[3]对普通交错网格和旋转交错网格进行了讨论，发现由于差分阶数较低，要达到一定的计算精度同样需要增加最小波长中的网格数；熊章强等^[4]的研究主要集中在边界处理方面，采用PML吸收边界条件以消除边界反射，取得了较好的效果，但其采用2×12阶高精度交错网格有限差分法必然导致计算效率降低。以上研究大多采用有限差分方法对瑞雷波进行数值模拟，而数值(网格)频散是有限差分模拟不可回避的问题，究其原因，是因为基于波动方程的有限差分求解过程通常是利用1个离散化的差分方程去逼近波动方程，从而使得相速度变成离散空间间隔的函数。因此，当每一波长内空间采样太少(即粗网格)时，就会产生数值频散，其实质是一种因离散化求解波动方程而产生伪波动^[5]。为了压制数值频散，Dablain^[6]对声波二阶空间差分的数值模拟进行了分析，指出网格大小和传播方向是影响频散的重要因素；蔡其新等^[7]就高阶差分、优化差分参数和通量校正传输(FCT)等方面对压制频散进行了讨论，提出了最小频散算法；吴国忱等^[8]从空间离散、时间离散和算子近似3方面对TI介质中波场模拟产生的频散进行分析，并对压制数值频散的方法进行讨论；孙成禹等^[9]就空间采样间隔、传播距离及速度等因素对频散的影响进行了定量分析，并指出了由频散导致的假频现象及其主要特点。在此，本文作者针对瑞雷波有限差分模拟中的数值频散现象，通过通量校正传输方法对其进行压制，分析和解释波场特征，并对计算效率进行     讨论。

1  二维一阶弹性波波动方程及其差分格式

1.1  波动方程

在二维均匀各向同性弹性介质中，一阶速度-应力标量弹性波波动方程组为^[10]：

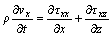             (1a)

             (1b)

          (1c)

          (1d)

             (1e)

其中：v_x和v_z分别为质点振动速度在x和z方向的分量；τ_xx和τ_zz分别为质点在x和z方向的正应力；τ_xz为质点在xz平面内的剪应力；ρ为介质的密度；μ为介质的剪切摸量，与λ一并统称为拉梅常数。

1.2  差分格式

交错网格是指把速度v和应力τ分别定义于2套不同网格上的网格系统，其优点在于能够很好地处理一阶波动方程中速度和应力的耦合关系。图1所示即为其网格剖分方案。

图1  交错网格剖分示意图

Fig.1  Scheme of staggered

本文采用时间二阶和空间四阶的差分格式，差分格式如下：

        (2a)

 (2b)

(2c)

其中：D_t，D_x和D_z分别为对t，x和z的差分离散算子；为v_x，v_z，τ_xx，τ_zz和τ_xz的集合；a₁=1.125；a₂=-0.041 666 67。对波动方程(1a~1e)进行差分离散，离散方程组如下：

    (3a)

          (3b)

            (3c)

            (3d)

 (3e)

其中：U和V分别为v_x和v_z的离散量；R，T和H分别为τ_xx，τ_zz和τ_xz的离散量；B为ρ^-1的离散值。

2  边界条件及稳定性条件

2.1  自由边界

在进行瑞雷波数值模拟时，自由边界能否得到很好处理将直接决定着模拟效果。本文在自由边界采用空间四阶差分精度，用镜像法和零速度法进行处    理^[11]。

对于二维模型，自由边界条件(z=0)为τ_xz=0，τ_zz=0。当采用高阶差分格式时,为了保证在自由边界条件(z=0)成立，则τ_zz和τ_xz在高阶差分算子的长度上一定是关于z=0反对称的，这就是镜像原理。设定v_x，τ_xx和τ_zz位于自由界面，并在自由界面上设置2层真空层(v_s和v_p为0 m/s)，此时，自由界面存在一反射界面，从而使得球面波在界面反射产生瑞雷波。速度分量U和V计算时满足：

；l=1，2        (4a)

           (4b)

                (4c)

2.2  吸收边界

吸收边界条件广泛应用于无边界介质中的波场模拟，以减少来自人工边界的反射。关于吸收边界条件已有较多的讨论，完全匹配层(PML)吸收边界条件是消除边界反射的理想方法之一，其实质是理论上假设存在一种各项异性有耗介质(PML层)，适当选取参数可使任意频率、任意极化的波以任意入射角通过它与自由空间的交界面时相速度和特征阻抗均不变，从而达到与自由空间完全匹配，入射波进入PML层后迅速衰减，理论上不产生任何反射。本文采用文献[4]中的方法对人工边界进行处理。

2.3  稳定性条件

二维均匀各向同性弹性介质，差分精度为O(Δt²+Δx⁴)，Δx=Δz，其稳定性条件为^[12]：

                (5)

3  FCT方法

FCT(Flux-corrected transport)方法又称通量校正传输，由Boris等^[13]提出。该方法有效压制了粗网格情况下差分计算产生的数值频散和数值震荡。FCT方法是基于守恒型方程的差分格式，要求网格间交界面处守恒物理量的通量相互抵消，即交界面两侧一边流出和另一边流出的通量相等。其基本原理是：假设所有的极值点都是由数值频散引起的，对所有网格点进行漫射校正处理，达到消除数值频散的效果；再对非局部极值点进行补偿的反漫射校正，使任何不需要漫射的地方得到恢复，反漫射校正是非线性的。Tong  等^[14]将FCT方法应用于基于波动方程的波场数值模拟，很好地压制了数值频散；杨顶辉等^{[5, 15]}将FCT方法应用于求解各向异性波动方程组；郑海山等^[16]采用有限差分法，结合FCT方法和幅值限制器对横向各向同性介质的二维非线性弹性波进行数值模拟，均有效地压制了传统有限差分数值模拟中的数值频散,取得了较好的模拟效果。

对于一阶速度-应力波动方程，在应用FCT方法对差分数值解进行校正的过程中，只需对和进行计算，因为在完成对和的校正后，通过方程3(c)~3(e)对，和进行了校正。FCT方法计算步骤如下(它适用于二维一阶速度-应力波动方程的有限差分计算)。

(1) 利用有限差分公式3(a)和3(b)计算所对应的差分数值解，k≥1。

(2) 计算第k-1时间层的漫射通量：

，0≤η₁≤1

，0≤η₁≤1

其中：η₁为漫射参数，它为常量或为１个线性函数，其取值取决于有限差分阶段频散误差，在数值试验中，控制0.008≤η₁≤0.100(当η₁小于0.008时，已失去压制频散的效果；当其大于0.100时，真实波场已被平滑模糊不清，分辨率显著下降)；0.01≤η₁≤0.05段比较合适，模拟效果较好，本文中η₁=0.010。

(3) 对第k+1时间层的反漫射进行校正：

 ，0≤η₂≤1

，0≤η₂≤1

η₂的取值与η₁的取值不同。这是由于传统有限差分运算引起的频散，又有人为加入的漫射。反漫射运算不仅要补偿人为加入射引起的损失，而且要补偿传统有限差分运算带来的振幅损失。因此，η₂的取值应比η₁大10%~15%。本文中，η₁=0.012。

(4) 利用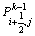和对第k+1时间层的进行漫射校正：

(5) 利用来计算反漫射通量：

；

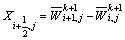(6) 利用和反漫射通量求取校正后的：

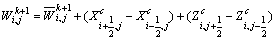
其中：

，。

4  数值模拟算例

为更加接近实际地模拟浅层各向同性弹性介质的全波场，选取较小的网格间距，给定较低的纵横波速，但低速地层更容易产生数值频散和假频^[11]，因此，采取有效措施以消除数值频散很有必要。设计模型宽×深为200 m×150 m，纵横向空间采样间隔均为1 m，时间采样间隔为0.2 ms，震源采用主频30 Hz的Ricker子波，置于第100号检波点处，埋深0 m。

4.1  模型1——均匀半空间介质模型

均匀介质物性参数分别为：密度ρ=2.0 g/cm³，纵波速度v_p=1.5 km/s，横波速度v_s=800 m/s。图2(a)和(b)所示是未进行FCT方法校正的快照图和单炮记录，图3(a)和(b)所示是经FCT方法处理后的快照图和单炮记录(图中，D，SW，S，P，P-S和PP分别代表直达波、面波、横波、纵波、P-S头波和纵波反射波，记录和快照显示的都是v_z分量，下同)。

图2  未加入FCT方法的60 ms时的快照(a)和模拟单炮记录

Fig.2  Snaps at 60 ms and synthetic single-shot record without using FCT method

对比图2和图3可以看到：传统有限差分模拟造成比较严重的频散情况，而加入FCT方法后，数值频散得到有效压制，更接近于真实波场。图3显示：在均匀半空间介质中，瑞雷波不发生频散现象。

4.2  模型2——含低速夹层的介质模型

表1所示为含低速夹层的层状介质模型参数，图4(a)和(b)所示是未进行FCT方法处理的快照图和单炮记录，图5(a)和(b)所示是经FCT方法处理后的快照图和单炮记录。

图3  加入FCT方法后的60 ms时的快照和模拟单炮记录

Fig.3  Snaps at 60 ms and synthetic single-shot record by using FCT method

表1  含低速夹层的层状介质的模型参数

Table 1  Model parameters of layered media with a low velocity interlayer

不同频率的波在介质中以不同的速度传播的现象称为波的频散，频率ω和波数k之间的关系ω(k)称为频散关系。波的频散主要包括数值(网格)频散和物理频散。数值频散是由于网格离散的截断误差导致群速度和相速度依赖于波的频率，它是一种伪波动，表现为波在传播过程中波前形状发生变化,并且逐渐散开；物理频散是指由于物理介质不同，波传播相速度随波数发生变化的现象。瑞雷波在层状介质中传播发生的频散属于物理频散。

图4  未加入FCT方法的100 ms时刻的快照(a)和模拟单炮记录

Fig.4  Snaps at 100 ms and synthetic single-shot record without using FCT method

对比图4(a)和图5(a)可见：对于图4(a)中2个矩形区域，由于各层之间的多次反射造成振荡和网格频散相混淆，不能清晰地分辨真实波场，经FCT方法处理后，图5(a)中各反射波层次比较清楚，网格频散被压制，而真实的反射波场被保留。

对比图4(b)和图5(b)可见：图4(b)中三角形区域网格频散现象突出，干扰了真实波场；图5(b)中，由于消除了相应区域的网格频散，使得瑞雷波的频散特征更加清晰。

图5  加入FCT方法的100 ms时的快照和模拟单炮记录

Fig.5  Snaps at 100 ms and synthetic single-shot record by using FCT method

图5(a)和图5(b)中，波场快照中显示的各类波在单炮记录里有良好的反映，印证了经过FCT方法后，网格频散被压制，真实波场被凸显。这是因为网格频散主要是以接近于Nyquist频率的高频成分引起的，而真实波场主要是低频成分。FCT方法往往会压制那些接近于Nyquist频率的数值频散，同时恢复大部分真实波场^[14]。因此，FCT方法不会破坏真正的波场振荡，它压制的是数值频散，而不是在层状介质中瑞雷波产生的频散。

5  计算效率分析

模型3和模型4的宽×深为400 m×300 m，均匀介质物性参数分别为：密度ρ=2.0 g/cm³，纵波速度v_p=1.2 km/s，横波速度v_s=650 m/s。模型3是粗网格下的FCT模型，模型4是细化网格模型，其具体参数和计算效率见表2。为压制频散，模型3计算时间为473 s，模型4计算时间为1 096 s, 使用FCT方法所得计算效率比细化网格来压制频散的计算效率提高了1.3倍，具有明显的优势；另外，在效果方面，图6(a)中还存在部分频散现象，而6(b)没有频散现象，FCT方法压制频散效果比细化网格方法的优。

图6  模型3和模型４在160 ms时的快照

Fig.6  Snap at 160 ms of models 3 and 4

表2  2个模型的参数及计算时间

Table 2  Parameters and computing time of models 3 and 4

6  结论

(1) 将FCT方法应用于瑞雷波的数值模拟中。该方法很好地压制了离散网格带来的数值频散现象，同时保证了真实的震波场震荡，使瑞雷波在层状介质中传播产生的频散现象被凸显，能更准确、直观地了解瑞雷波的传播特征。

(2) FCT方法的引入虽然增加了计算量，但在达到同一精度时，与细化网格相比，FCT方法的计算效率提高了1.3倍，为解决粗网格下瑞雷波的有限差分模拟中出现的数值频散问题提供了一种快速有效的方法。此外，在FCT方法中漫射与反漫射步骤可以引入代码并行计算，计算效率还将进一步提高。

(3) 建议将模拟中得到的波场数据进行处理，提取频散曲线，反演模型地层参数，验证数值模拟的正确性和频散压制的可靠性。

参考文献：

[1] 周竹生, 刘喜亮, 熊孝雨. 弹性介质中瑞雷面波在有限差分正演模拟[J]. 地球物理学报, 2007, 50(2): 567-573.
ZHOU Zhu-sheng, LIU Xi-liang, XIONG Xiao-yu. Finite-difference modeling of Rayleigh surface wave in elastic media[J]. Chinese Journal of Geophysics, 2007, 50(2): 567-573.

[2] XU Yi-xian, XIA Jiang-hai, Miller R D. Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach[J]. Geophysics, 2007, 72(5): 147-153.

[3] Bohlen S R. Accuracy of heterogeneous staggered-grid finite-difference modeling of Rayleigh waves[J]. Geophysics, 2006, 71(4): T109-T115.

[4] 熊章强, 张大洲, 秦臻, 等. 瑞雷波数值模拟中的边界条件及模拟实例分析[J]. 中南大学学报: 自然科学版, 2008, 39(4): 824-830.
XIONG Zhang-qiang, ZHANG Da-zhou, QIN Zheng, et al. Boundary conditions and case analysis of numerical modeling of Rayleigh wave[J]. Journal of Central South University:Science and Technology, 2008, 39(4): 824-830.

[5] 杨顶辉, 腾吉文. 各向异性介质中三分量地震记录的FCT有限差分模拟[J]. 石油地球物理勘探, 1997, 32(2): 181-189.
YANG Ding-hui, TENG Ji-wen. FCT finite difference modeling of three-component Seismic records in anisotropic medium[J]. Oil Geophysical Prospecting, 1997, 32(2): 181-190.

[6] Dablain M A. The application of high-order differencing to scalar wave equation[J]. Geophysics, 1986, 51(1): 54-66.

[7] 蔡其新, 何佩军, 秦广胜, 等. 有限差分数值模拟的最小频散算法及其应用[J]. 石油地球物理勘探, 2003, 38(3): 247-251, 262.
CAI Qi-xin, HE Pei-jun, QIN Guang-sheng, et al. Minimum dispersion algorithm by finite-difference numeric modeling and its applications[J]. Oil Geophysical Prospecting, 2003, 38(3): 247-251, 262.

[8] 吴国忱, 王华忠. 波场模拟中的数值频散分析与校正策略[J]. 地球物理学进展, 2005, 20(1): 58-65.
WU Guo-chen, WANG Hua-zhong. Analysis of numerical dispersion in wave-field simulation[J]. Progress in Geophysics, 2005, 20(1): 58-65.

[9] 孙成禹, 宫同举, 张玉亮, 等. 波动方程有限差分法中的频散与假频分析[J]. 石油地球物理勘探, 2009, 44(1): 43-48.
SUN Chen-yu, GONG Tong-ju, ZHANG Yu-liang, et al. Analysis on dispersion and alias in finite-difference solution of wave equation[J]. Oil Geophysical Prospecting, 2009, 44(1): 43-48.

[10] 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419.
DONG Liang-guo, MA Zai-tian, CAO Jin-zhong, et al. A staggered-grid high-order difference method of one-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(3): 411-419.

[11] 裴正林. 任意起伏地表弹性波方程交错网格高阶有限差分法数值模拟[J]. 石油地球物理勘探, 2004, 39(6): 629-634.
PEI Zheng-lin. Numerical modeling using staggered-grid high order finite-difference of elastic wave equation on arbitrary relief surface[J]. Oil Geophysical Prospecting, 2004, 39(6): 629-634.

[12] 董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报, 2000, 43(6): 856-864.
DONG Liang-guo, MA Zai-tian, CAO Jin-zhong. A study on stability of the staggered-gird high-order difference method of first-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(6): 856-864.

[13] Boris J P, Book D L. Flux-corrected transportⅠ: SHASTA, a fluid transport algorithm that works[J]. Journal of Computational Physics, 1973, 11(1): 38-69.

[14] Tong Fei, Larner K. Elimination of numerical dispersion in finite-difference modeling and migration by flux-corrected transport[J]. Geophysics, 1995, 60(6): 1830-1842.

[15] Yang D H, Liu E, Zhang Z J, et al. Finite-difference modeling in two-dimensional anisotropic media using a flux-corrected transport technique[J]. Geophysical Journal International, 2002, 148(2): 320-328.

[16] 郑海山, 张中杰. 横向各向同性(VTI)介质中非线性地震波场模拟[J]. 地球物理学报, 2005, 48(3): 660-671.
ZHENG Hai-shan, ZHANG Zhong-Jie. Synthetic seismograms of nonlinear seismic waves in anisotropic (VTI) media[J]. Chinese Journal of Geophysics, 2005, 48(3): 660-671.

(编辑 陈灿华)

收稿日期：2011-06-27；修回日期：2011-09-05

基金项目：国家自然科学基金资助项目(40804027，41074085)；湖南省自然科学基金重点资助项目(09JJ3084)

通信作者：丰赟(1983-)，男，湖北罗田人，硕士，助理工程师，从事工程物探和地震数值模拟研究；电话：13980713421；E-mail：    geophy.fy@gmail.com