一种基于电离层变化率的单频载波相位平滑伪距改进方法
徐博，刘文祥，廖鸣
(国防科技大学 电子科学与工程学院，湖南 长沙，410073)
摘要：为了避免单频用户可能出现的发散问题。在单频载波相位平滑伪距中，基于电离层延迟模型对电离层延迟变化进行补偿，进而推导该方法平滑后伪距精度的数学模型，使用IGS实测数据进行算例分析，验证本文方法的有效性。结果表明：本文改进的算法明显优于传统单频载波相位平滑伪距法。
关键词：卫星导航；单频载波相位平滑伪距；电离层延迟变化率
中图分类号：TN967.1 文献标志码：A 文章编号：1672-7207(2014)02-0464-04
An improved method of single frequency carrier phase smoothing pseudo
XU Bo, LIU Wenxiang, LIAO Ming
(School of Electronic Science and Engineering, National University of Defense Technology, Changsha 410073, China)
Abstract: To avoid the divergence problem of single-frequency users, a single frequency carrier phase smoothing method was put forward, which uses pseudo ionospheric delay model to compensate the ionosphere delay variation. It derived the mathematical model smoothing the pseudorange, and the IGS measured data were used to verify the effectiveness of the method. The results show that the method proposed is greater than the traditional single frequency carrier phase smoothed pseudo method.
Key words: satellite navigation; single frequency carrier phase smoothed pseudo; ionospheric delay variation compensation
卫星导航系统有伪码伪距和载波相位2种距离观测量，载波相位比伪距的测量精度高1~2个数量级，且受多径信号的影响较小，但是存在整周模糊度的解算问题，限制了载波相位的高精度实时应用。伪距测量不存在整周模糊度，但其测量精度不高，且容易受多径信号的影响，利用载波相位平滑伪距可吸收两种观测量优点，提高观测精度。因此，在实时高精度应用场合中，利用高精度的载波相位观测量对伪距进行平滑是提高伪距精度的有效方法。单频载波相位平滑方法就是根据载波相位整周模糊度和电离层延迟在一定时间内近似不变，利用高精度单频载波相位的变化来辅助平滑伪距，以提高伪距测量精度[1]。成本低廉的单频接收机应用市场非常广泛，故单频载波相位平滑伪距技术得到国内外学者较多的关注。由于电离层对伪距和载波相位的影响相反，单频载波相位平滑过程中存在电离层误差平滑发散的问题，文献[2-3]分别研究了利用线性滤波器和非线性过程来设计减弱电离层发散误差的平滑方法。文献[4-5]研究了优化平滑时间长度的不同方法，来减小单频相位平滑伪距的稳态误差，即便如此单频相位平滑伪距的发散问题仍不可避免。本文作者提出一种简单有效的补偿方法，单频用户通过klobuchar模型补偿电离层延迟变化，可大大减小单频相位平滑伪距的偏离误差，并通过实验数据验证了补偿方法的有效性。该方法用较小的代价，获得了较大的平滑性能提升。在给定输入参数的情况下得出了最优参数，在此基础上讨论最优参数随输入信号载噪比、最大多普勒容限以及导频功率系数的变化规律。
1 传统单频Hatch平滑算法
1.1 算法原理
伪距和载波相位观测方程为：
(1)
(2)
其中：ρ(t)为观测伪距；f(t)和φ(t)分别载波相位的距离和周数；R(t)为卫星与接收机间几何距离；△tr(t)为接收机钟差；△ts(t)为卫星钟差；c为光速；I(t)为电离层延迟；T(t)为对流层延迟；λ为该频点载波波长；N为整周模糊度(假定平滑过程中未发生周跳，N为常数，若检测到周跳，则须重新启动平滑过程)；ερ(t)为伪距中多径和随机误差；εL(t)为载波相位中多径和随机误差，假定它们都为高斯白噪声，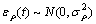
，
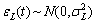，且ερ(t)和εL(t)相互独立。
Hatch滤波是传统单频载波平滑伪距的常用处理方法。单频平滑(Hatch滤波)存在2种形式，其对应的历元间平滑处理为：
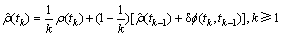(3)
(4)
其中：M为滤波器长度，根据平滑时间T和观测采样间隔τ取定，
；
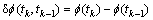，平滑起始值为
1.2 性能分析
为叙述方便，记(1)右边除了测量噪声ερ(t)外的其他5项为
(5)
则
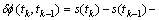
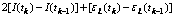(6)
记第ｋ历元和k-1历元的电离层延迟变化为
平滑后伪距残差为
(7)
根据式(1)，(2)，(4)和(7)可得
(8)
根据式(8)分别计算e(tk)的均值和方差：
(9)
(10)
由此可得，平滑后伪距残差的均值偏移为
(11)
平滑后伪距的方差为
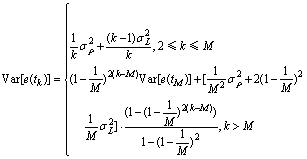(12)
当k趋于无穷大时，就得到平滑后伪距的稳态方差为
(13)
为了得到更好的平滑伪距性能，要求同时减小均值偏移和稳态方差，但是减小稳态方差与减小均值偏移是一对矛盾：要减小稳态方差，则需要增加M，而增加M，均值偏移会增大。
2 改进的单频平滑方法
传统平滑算法中平滑后伪距残差的均值发生偏移，偏移量是各历元电离层延迟变化、滤波器长度M的函数，其稳态方差与滤波器长度M、载波相位测量方差和伪距测量方差有关。对此，本文提出一种改进的单频载波相位平滑伪距方法，基于Klobuchar模型估计电离层延迟变化来补偿平滑后伪距残差的均值偏移。
传统单频平滑方法伪距残差的均值发生偏移，本质上是由于电离层对载波相位测量和伪距测量的影响相反。Klobuchar模型是一个被单频接收机广为采用的电离层延迟改正模型，它将夜间的电离层时延视为常数，而白天的电离层延迟则用余弦函数中正的部分来模拟，GPS就是采用该模型来校正单频用户的电离层延迟。用Klobuchar模型估计电离层对GPS L1信号的时间延迟(s)[6]可表达为：
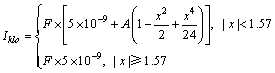(14)
式中，A为振幅，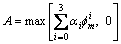
；x=2π(tl-50 400)/P；
；F为倾斜因子；tl为本地时间；
为电离层穿透点IPP的地磁纬度(以半圆为单位)，它们的计算可以参考文献[6]。αi和βi(i=0，1，2，3)为编入导航电文播发给用户的模型参数。
根据Klobuchar模型估计第k历元和k-1历元的电离层延迟变化为
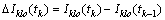(15)
用以补偿平滑伪距残差的均值偏移，第k历元的平滑可改进为
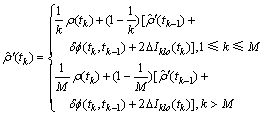(16)
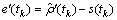(17)
易证得改进后均值偏移为
(18)
由于
是模型计算值，不含观测过程，它只影响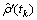
残差的均值变化，而不影响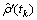残差的方差计算，因此其稳态方差仍由式(13)描述。
3 实验与仿真
使用GPS测站数据，采样时间间隔为30 s，观测数据类型为C1和P2。将C1的数据通过Klobuchar估计出的电离层延迟与通过C1和P2双频估计的电离层延迟进行比较[7-8]，结果如图1所示。从图1可见：2种方法的电离层延迟趋势基本一致。
由于采用单频载波平滑伪距后的伪距均值偏移和电离层延迟变化率有关，对图1的2个估计值取斜率，得到2种方法电离层延迟变化率如图2所示。从图2可见：这2种方法得到的电离层延迟变化率差异较小，因此，通过Klobuchar估计出的电离层延迟变化率可为单频载波平滑伪距进行有效补偿。
图1 电离层延迟
Fig. 1 Ionospheric delay
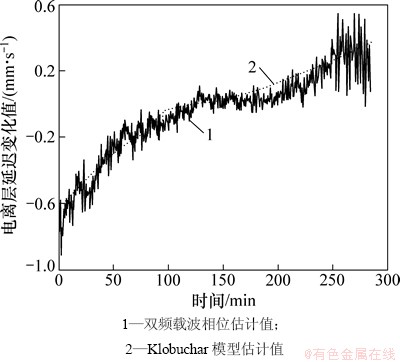
图2 电离层延迟变化
Fig. 2 Change of ionospheric delay
图3 2种单频载波平滑伪距方法的平滑后伪距误差
Fig. 3 Pseudo-range error after smoothing of two calculation methods
对使用Klobuchar方法修正的伪距进行单频载波相位平滑伪距，与传统方法进行的单频载波相位平滑伪距进行比较，本文改进算法明显优于传统平滑算法。
4 结论
(1) 提出在单频载波相位平滑伪距中基于电离层延迟模型对电离层延迟变化进行补偿，避免单频用户可能出现的发散问题。
(2) 使用Klobuchar方法改进后的单频载波相位平滑伪距方法的伪距精度和电离层延迟的变化率有关。
(3) 使用Klobuchar方法计算的电离层延迟变化率和使用双频修正方法计算的电离层延迟变化一致。
(4) 本文的改进算法明显优于传统单频载波相位平滑伪距方法。
参考文献：
[1] 何海波, 郭海荣, 李保利. 广域差分参考站两种伪距平滑算法的再评估[J]. 测绘学院学报, 2005, 22(3): 157-159.
HE Haibo, GUO Hairong, LI Baoli. Re-evaluation of two carrier smoothed code algorithms for WADGPS reference stations[J]. Journal of Institute of Surveying and Mapping, 2005, 22(3): 157-159.
[2] Rife J, Sen S. Design of a single-frequency filter that minimizes ionosphere divergence error[C]//ION GNSS 2007, Fort Worth, 2007: 368-378.
[3] Sen S, Rife J. Reduction of ionosphere divergence error in GPS code measurement smoothing by use of a non-linear process[C]//IEEE PLANS 2008. Piscataway: IEEE, 2008: 312-320.
[4] Park B, Kee C. Optimal hatch filter with a flexible smoothing window width[C]//ION GNSS 2005. Long Beach: Institute of Navigation, 2005: 592-602.
[5] Kim E, Walter T. Adaptive carrier smoothing using code and carrier divergence[C]//ION NTM 2007. San Diego: Institute of Navigation, 2007: 141-152.
[6] IS-GPS-200 D, Navstar GPS Space Segment/Navigation User Interfaces[S].
[7] McGraw G A, Young R S Y. Dual frequency smoothing DGPS performance evaluation studies[C]//ION NTM 2005. San Diego: Institute of Navigation, 2005: 170-181.
[8] McGraw G A. Generalized divergence-free carrier smoothing with applications to dual frequency differential GPS[J]. Navigation, 2009, 56(2): 115-122.
(编辑 赵俊)
收稿日期：2013-05-15；修回日期：2013-08-10
基金项目：新世纪优秀人才支持计划基金资助项目(NCET-04-0995)
通信作者：徐博(1982-)，男，河南洛阳人，博士，从事星基导航与定位技术研究；电话：13787313231；E-mail：xubo973109@sina.com
