J. Cent. South Univ. (2020) 27: 1907-1916

DOI: https://doi.org/10.1007/s11771-020-4419-6

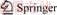
Seepage characteristics of a fractured silty mudstone under different confining pressures and temperatures

FU Hong-yuan(付宏渊)¹, JIANG Huang-bin(蒋煌斌)¹, QIU Xiang(邱祥)²,JI Yun-peng(姬云鹏)², CHEN Wen(陈文)³, ZENG Ling(曾铃)²

1. School of Traffic & Transportation Engineering, Changsha University of Science & Technology,Changsha 410114, China;

2. School of Civil Engineering, Changsha University of Science & Technology, Changsha 410114, China;

3. Laboratoire d'Etude des Microstructures et de Mécanique des Matériaux, Université de Lorraine,Metz 57070, France

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020

Abstract: To investigate the influence of confining pressures and temperatures on the seepage characteristics of fractured rocks, seepage tests were conducted on a fractured silty mudstone using a self-developed experimental system, and the effects of different factors on coefficient of permeability were discussed. The results showed that the increasing confining pressure will gradually decrease the coefficient of permeability, and this process is divided into two stages: 1) the fast decrease stage, which corresponds to a confining pressure less than 30 kPa, and 2) the slow decrease stage, which corresponds to a confining pressure larger than 30 kPa. Unlike confining pressure, an increase in temperature will increase the coefficient of permeability. It is noted that fracture surface roughness will also affect the variation of coefficient of permeability to a certain extent. Among the three examined factors, the effect of confining pressure increases is dominant on fracture permeability coefficient. The relationship between the confining pressure and coefficient of permeability can be quantified by an exponential function.

Key words: silty mudstone; seepage characteristic; confining pressure; temperature; permeability

Cite this article as: FU Hong-yuan, JIANG Huang-bin, QIU Xiang, JI Yun-peng, CHEN Wen, ZENG Ling. Seepage characteristics of a fractured silty mudstone under different confining pressures and temperatures [J]. Journal of Central South University, 2020, 27(7): 1907-1916. DOI: https://doi.org/10.1007/s11771-020-4419-6.

1 Introduction

As a typical discontinuous medium, the soft rock has a large number of fracture structures inside, which enable fluid media such as rainwater, groundwater, oil, and gas to move inside [1-3]. Because of the influence of external factors such as pressure and temperature, the characteristics of fractures in rock is prone to change, resulting in large changes in coefficient of permeability [4-6]. This change caused a seepage mutation in fractured rock, which affected the stability and safety of the engineering slopes.

The permeability of fractured rocks shows obvious anisotropy, and the influencing factors are very complex and difficult to determine [7-11]. The seepage characteristics of fractured rocks under complex external conditions have received much attention, and various approaches including theoretical calculations [12, 13] and physical model tests [14] have been developed. The earliest theoretical formulas were derived based on the laminar flow theory. Although subsequent studies proposed many improved formulas, most of them do not depart from the laminar flow theory. Actually, since the fractured surface of a natural rock is very rough, the type of seepage should be turbulent flow. For this reason, the research results obtained from theoretical calculations usually deviate from the real situation. In physical model tests, if the characteristics of fractures are carefully taken into account, the real seepage field may be simulated, which makes the physical model test be one of the most important and direct study ways in this field. RAU et al [15] revealed the permeability characteristics of a fractured sandstone under different head differences using a seepage test device made of plexiglass materials. The laboratory experiments of SHARMEEN et al [16] and QIAN et al [17] showed that, the coefficient of permeability the rock with a single fracture is affected by the head pressure and fracture aperture in addition to the fracture surface roughness. Moreover, they obtained an exponential function of the hydraulic gradient to characterize the fracture permeability coefficient. LIU et al [18] developed a seepage test system for fractured rocks and used transparent glass materials to prepare samples with different fracture forms. The influence of fracture properties on the critical hydraulic gradient of the fractured rock under changed head difference was studied. The results of those physical model tests helped understand the seepage characteristics of fractured rocks to some extent. However, the interaction between the stress field and the seepage field was seldom considered. Actually, the neglect of this interaction will make the obtained results different from the real values. In addition, some scholars found that both lower and higher temperatures can lead to changes in coefficient of permeability of rocks [19, 20]. Especially, in the southern part of China where the weather is hot and humid, the influence of temperature on the seepage characteristics of soft rock slopes needs to be considered.

To this end, seepage tests considered the effects of both stress and temperature were conducted on fractured silty mudstone samples collected from the shallow layer of slope. The seepage characteristics of fractured silty mudstones with different confining pressures, temperatures and fractured surface roughnesses were analyzed.

2 Experimental details

2.1 Material

In this work, silty mudstones with good integrity were manually excavated from the shallow layer of slope in Liuyang City, China. They were then immediately wrapped with cling film to prevent rapid drying. The silty mudstone mainly contains quartz, illite, montmorillonite, chlorite and feldspar. The major chemical composition includes SiO₂, Al₂O₃, Fe₂O₃, K₂O, MgO, TiO₂ and Na₂O, of which the mass fraction of SiO₂ and Al₂O₃ accounts for about 80%. The main physical properties of the silty mudstone were measured by geotechnical tests. The results showed that the dry density of the silty mudstone is 2.3 g/cm³ and the porosity of the silty mudstone is 18.5%.

2.2 Preparation of fractured silty mudstone samples

A series of d50 mm×32 mm cylindrical rock samples were extracted from the cores of the collected silty mudstones. Then, cylindrical rock samples were laid down and placed between the loading plates of the compression testing machine. A steel bar having a diameter of 1 mm was placed at each position where the sample was in contact with the upper or lower loading plate. The steel bar can transfer the surface load (i.e., pressure) applied on the loading plate to the line load exerting on the side surface of the sample, so the rock sample was broken into two parts (Figure 1) along the line load direction by the tensile stress during the compression test. Consequently, the two half-cylindrical parts were combined along the failure surface to form a fractured silty mudstone sample.

2.3 Characterization of fracture surface

To characterize the fracture morphology, the fracture surfaces were scanned by the Tianyuan 3D laser scanner jointly developed by Beijing Tianyuan 3D Technology Co., Ltd. and Tsinghua University. As shown in Figure 1, the 3D scanning process of the fractured silty mudstone sample was as follows: 1) Some circular paper labels with a diameter of 5 mm were pasted at random positions on the top and side of the sample as calibration points for scanning; 2) The fracture surfaces of the samples were scanned by a 3D scanner. Afterward, the 3D scanning images were optimized by the MATLAB software package, and the fracture parameters, such as the length (L), width (w), aperture (b_m), and maximum height (h) of the fracture surface, were acquired. Additionally, the arithmetic average deviation (S_a) that represents the arithmetic mean of the distances from the concave point and convex point of the fracture surface to the center plane of the fracture was obtained; it is an important index to reflect the fracture surface roughness. Table 1 shows the fracture parameters of six typical samples. These samples have arithmetical average deviations vary from 0.26 to 0.76, and thus they were numbered J1-J6 in order of fracture surface roughness from small to large.

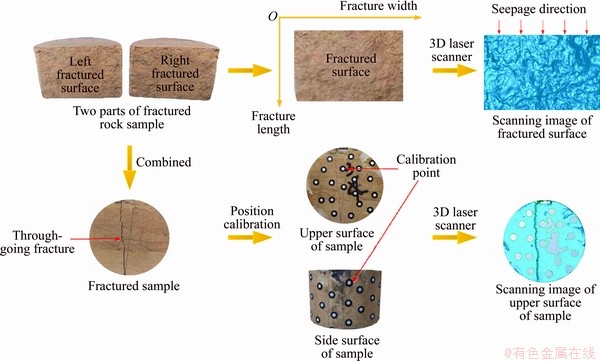
Figure 1 Schematic diagram of 3D scanning process

2.4 Experimental device

A seepage test device capable of simulating different confining pressures and temperatures was developed to investigate the seepage characteristics of the fractured silty mudstone. As shown in Figure 2, the experimental device is mainly composed of a test chamber, a seepage chamber, and a seepage flow monitoring system.

Table 1 Fracture parameters of fractured silty mudstone samples

1) Test chamber

The temperature (0-60 °C, ±1 °C) and humidity (0-90%, ±1%) of the tests were controlled by a HWS-250B constant temperature humidity chamber (HNLX Ltd., HWS, China).

2) Seepage chamber

The seepage chamber consists of a fractured silty mudstone sample, ring rubber membranes, waterproof glue, a porous stone, and water. A ring rubber membrane with a thickness of 0.5 mm and the same diameter as the sample was wrapped on the side of the sample. Then, a layer of waterproof glue was evenly filled between the ring rubber membrane and the fractured silty mudstone sample. Because the height of the ring rubber membrane is 60 mm higher than that of the fractured sample, it forms a curtain for storing water on the upper surface of the fractured silty mudstone sample.

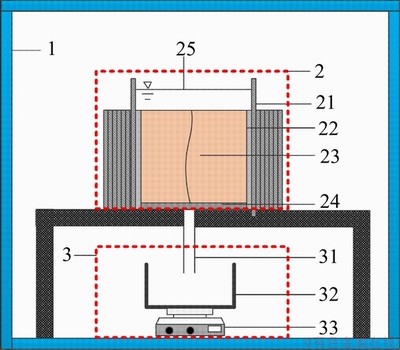
Figure 2 Experimental device (1-Test chamber; 2- Seepage chamber; 3-Seepage flow monitoring system; 21-Rubber membrane; 22-Waterproof glue; 23- Fractured sample; 24-Porous stone; 25-Water; 31- Discharging tube; 32-Water collector; 33-Electronic scale)

According to previous studies [21], the radial stress can be generated by changing the radial deformation of the ring rubber membrane, thereby creating a small confining pressure on the wrapped rock. In this study, different layers of ring rubber membranes were superimposed on the surface of the first ring rubber membrane. Because of the radial enlargement of ring rubber membranes, different low confining pressures were applied to the fractured silty mudstone samples. The relationship between the number of ring rubber membrane layers (n) and the confining pressure (p_r) (Figure 3) can be expressed by the following equation:

                            (1)

where p_z is the confining pressure, kPa; n is the number of rubber membrane layers; ε_rm is the hoop tensile strain of rubber membrane, mm; D is the internal diameter of rubber membrane, mm; E_m is the elastic modulus of rubber membrane, kPa.

3) Seepage flow monitoring system

The seepage flow monitoring system consists of discharging tube, water collector, and electronic scale. The water oozed from the fractured sample flows through the discharging tube into the water collector placed on an electronic scale. Thereafter, the seepage flow can be calculated based on the reading of the electronic scale.

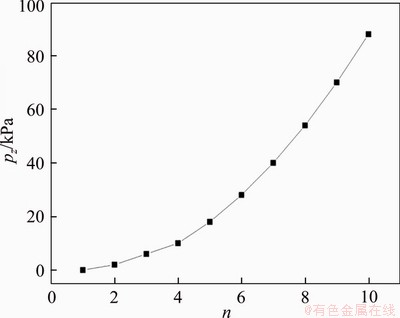
Figure 3 Correspondence between number of ring rubber membrane layers and confining pressure

2.5 Experimental method

In road engineering, the failures of soft rock cut slopes are commonly shallow. GUO et al [21] have shown that the stress state in the shallow slope is mostly less than 50 kPa. In this study, seepage tests were conducted on six samples with different fracture surface roughnesses under various confining pressures and temperatures. The temperature required for the experiment was set by the test chamber before the experiment. During the experiment, zero confining pressure (i.e., one ring rubber membrane) was first loaded on the side surface of the fractured silty mudstone sample. Then, the water storage tank of the seepage chamber was filled with distilled water at a depth of 40 mm. The water gradually seeped into the rock fracture under the action of gravity. When the seepage was stable, the confining pressure was raised to up 10 kPa by increasing the number of rubber membranes. Subsequently, the confining pressure was increased step by step according to the test program. Finally, the seepage flow (Q) of the fractured silty mudstone sample was measured by the seepage flow monitoring system. Thus, the coefficient of permeability of the silty mudstone samples was calculated by Eq. (2):

                             (2)

where h is the depth of ponded water, m; A is the cross-sectional area of fractured silty mudstone, m²; k is the coefficient of permeability.

3 Results and discussion

3.1 Confining pressures

The curves of coefficient of permeability- confining pressure are shown in Figure 4. The coefficient of permeability silty mudstone samples decreased as the confining pressure increased regardless of the fractured surface roughness and temperature. It is noted that as the coefficient of permeability decreases, the slope of the coefficient of permeability-confining pressure curve decreases, and the rate of decrease is fast first and then slow with the turning point corresponding to a confining pressure of 30 kPa. To further reflect the change of coefficient of permeability, the application of confining pressure is divided into the early stage (i.e., 0-30 kPa) and the late stage (i.e., 30-50 kPa). In the early stage, the decrease rate of coefficient of permeability with increasing temperature is 75%-89%, 73%-79% and 60%-70%, respectively. and in the late stage, the decrease rate of coefficient of permeability with increasing temperature is 50%-67%, 49%-61%, and 31%-55%, respectively.

Figure 4 Relationship between confining pressure and coefficient of permeability:

The main reason is that the interspace (i.e., fracture aperture) between two fracture surfaces is the main seepage channel in a fractured silty mudstone sample. At the early stage, the fracture aperture is gradually reduced and the seepage channel is narrowed under confining pressure, resulting in a considerable decrease in the coefficient of permeability. However, the two fracture surfaces cannot be further compressed as the confining pressure continues to increase. This causes only a slow decrease in the size of the seepage channel. Therefore, the rate of reduction of the coefficient of permeability in the late stage is smaller than that in the early stage.

3.2 Influence of fracture surface roughness

Figure 4(a) shows that the coefficients of permeability are discrete under the same confining pressure and a temperature of 10 °C. When the confining pressure is less than 30 kPa, the coefficient of permeability of the J1 sample is the largest (1.12×10^-2 cm/s) and that of the J6 sample is the smallest (0.56×10^-2 cm/s). However, as the confining pressure increases, the dispersion of the coefficient of permeability under the same confining pressure gradually decreases, which indicates that the influence of fracture surface roughness on the coefficient of permeability is reduced by the increasing confining pressure. As mentioned in Section 3.1, when the confining pressure is small, interspaces between the through- going fracture surfaces are relatively large; therefore, a seepage channel is formed inside the fractured sample. At this time, the flow velocity of water in the seepage channel is mainly affected by the resistance of the fracture surface. And the greater the fracture surface roughness is, the greater the resistance is, and the smaller the coefficient of permeability is. However, when the fracture aperture is compressed to a minimum, the seepage channel is blocked.

As shown in Figures 4(b) and 4 (c), the dispersion of the coefficients of permeability of six fractured silty mudstone samples significantly decreases as the confining pressure increases. To be more intuitive, this phenomenon is quantified by the standard deviation of the coefficients of permeability of these samples at three temperatures under the same confining pressure (see Figure 5). It can be seen that the standard deviation of the coefficient of permeability decreases with increasing temperature when the confining pressure is less than 30 kPa.

This is because an increase in temperature reduces the viscosity of water, thereby impairing the resistance of the fracture surface to the flow of water. When the temperature is 40 °C and the confining pressure is 50 kPa, the standard deviation of the coefficients of permeability approaches 0 cm/s, which means that the fracture surface roughness will no longer affect the coefficient of permeability when the temperature and confining pressure are large enough. In addition, the standard deviation-confining pressure curve exhibits a bimodal form, and the confining pressures corresponding to the two peaks are 10 and 40 kPa,respectively. The reason for this change is mainly because the increase in confining pressure destroys the fracture surface structure, which causes different changes in the seepage channel. This process is very complicated and needs further investigation.

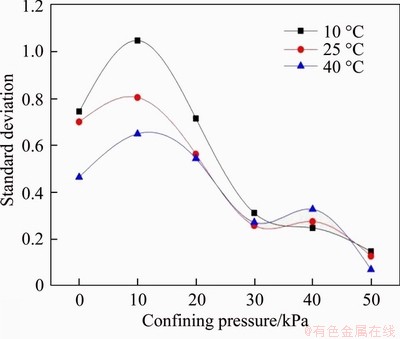
Figure 5 Relationship between confining pressure and standard deviation of coefficients of permeability

3.3 Influence of temperatures

As shown in Figure 6, the coefficient of permeability increases with increasing temperature under the same confining pressure. In addition, the dispersion of the coefficient of permeability- confining pressure curve tends to increase first and then decrease with increasing confining pressure when the samples have the same fracture surface roughness. For example, the maximum difference between coefficient of permeability of the J1 sample at three temperatures is 0.3×10^-2 cm/s when the confining pressure is 0 kPa; the maximum differences are 0.6×10^-2 cm/s and 0.4×10^-2 cm/s when the confining pressures are 30 and 50 kPa, respectively (Figure 6(a)).

As described in Sections 3.1 and 3.2, the fracture aperture gradually decreases as the confining pressure increases. At the early stage, water is able to flow freely in the seepage channel (i.e., fracture), the velocity of seepage is affected by the confining pressure, temperature and fracture surface roughness together. This leads to a large change in the coefficient of permeability of the six fractured silty mudstone samples when the confining pressure and temperature increases. At the later stage, the seepage channel of fracture is almost closed, and distilled water can only flow in the pores inside the rock [22-24]. In this case, the confining pressure and fracture surface roughness will gradually no longer affect the coefficient of permeability. Thus, the velocity of water flow depends on the single factor, i.e., temperature. Temperature affects the velocity of water flow by changing the viscosity of water, and its effect is very small. Therefore, the increase of temperature results in a small change in the coefficient of permeability of the six fractured silty mudstone samples.

The variation of the standard deviation of the coefficients of permeability of the six fractured silty mudstone samples under the same confining pressure is shown in Figure 7. Similarly, it can be found that the standard deviation of the fracture permeability coefficient is reduced by the confining pressure increasing.In addition, the standard deviation of the fracture permeability coefficient of the J1-J4 samples fluctuates only within a certain range, and do not significantly increase or decrease. It indicates that the effect of temperature on the fracture permeability coefficient is small when S_a is less than 0.56, and vice versa. However, when the confining pressure is 50 kPa, the standard deviation of the fracture permeability coefficient of the six fractured silty mudstone samples gradually tend to a steady value. It is proved again that the fracture surface roughness will no longer affect the fracture permeability coefficient when the temperature and confining pressure are large enough.

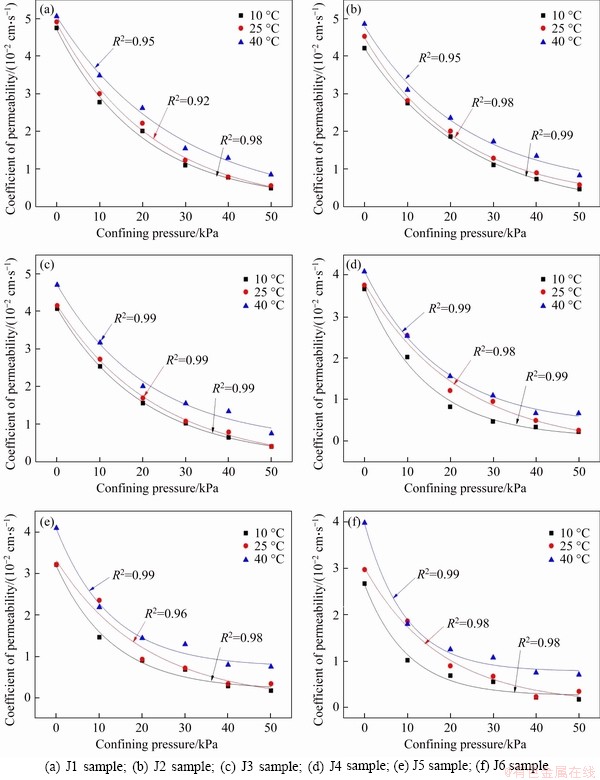
Figure 6 Coefficient of permeability-confining pressure curves:

Figure 7 Standard deviation of coefficient of permeability of six samples

3.4 Quantification

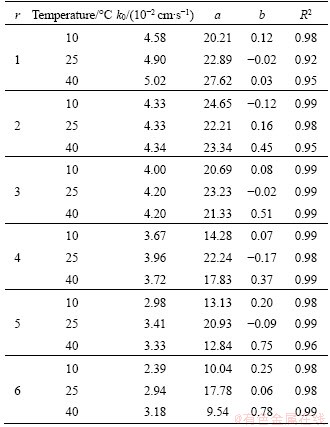
The coefficient of permeability fracture- confining pressure curves of the samples under different fracture surface roughness and temperature conditions can be fitted by a non-linear equation:

                             (3)

where k₀ is the initial coefficient of permeability when the confining pressure is zero, cm/s; a and b are fitting parameters (Table 2); p_c is the confining pressure, kPa.

As shown in Figure 6 and Table 2, all coefficients of determination (R²) are larger than 92%, suggesting that Eq. (3) can well quantify the relationship between the confining pressure and coefficient of permeability of the fractured silty mudstone at different fracture surface roughnesses and temperatures.

4 Conclusions

In this paper, a special seepage test device was introduced, and the seepage test results of fractured silty mudstone samples affected by the fracture surface roughness, confining pressures and temperature were presented.

1) Increasing confining pressure will cause the coefficient of permeability to gradually decrease,and this process is divided into two stages: 1) the fast decrease stage, which corresponds to a confining pressure less than 30 kPa, and 2) the slow decrease stage, which corresponds to a confining pressure larger than 30 kPa.

Table 2 Fitting parameters

2) Unlike confining pressure, an increase in temperature will cause coefficient of permeability to increase. However, the increasing confining pressure will reduce the effect of temperature on the coefficient of permeability.

3) Fracture surface roughness will also affect the variation of coefficient of permeability to a certain extent. The main reason is that the increasing confining pressure not only changes the size of the seepage channel, but also causes a slight change in the fracture surface roughness.

4) Among the three examined factors, the effect of confining pressure increase is dominant on fracture permeability coefficient. The relationship between the confining pressure and coefficient of permeability can be quantified by an exponential function.

References

[1] HUENGES E, KOHL T, KOLDITZ O, BREMER J, SCHECK-WENDEROTH M, VIENKEN T. Geothermal energy systems: research perspective for domestic energy provision [J]. Environmental Earth Sciences, 2013, 70(8): 3927-3933. DOI: 10.1007/s12665-013-2881-2.

[2] ZHANG J H, LI F, ZENG L, PENG J H, LI J. Numerical simulation of the moisture migration of unsaturated clay embankments in southern China considering stress state [J]. Bulletin of Engineering Geology and the Environment, 2020. DOI: 10.1007/s10064-020-01916-6.

[3] GAO Q F, JRAD M, HATTAB M, FLEUREAU J M. Pore morphology, porosity and pore size distribution in kaolinitic remoulded clays under triaxial loading [J]. International Journal of Geomechanics, 2020, 20(6): 1-10. DOI: 10.1061/(ASCE) GM.1943-5622.0001682.

[4] JAVADI M, SHARIFZADEH M, SHAHRIAR K, MITANI Y. Critical Reynolds number for nonlinear flow through rough-walled fractures: The role of shear processes [J]. Water Resources Research, 2014, 50(2): 1789-1804. DOI: 10.1002/2013WR014610.

[5] ZHANG J, PENG J, ZENG L, LI J, LI F. Rapid estimation of resilient modulus of subgrade soils using performance- related soil properties [J]. International Journal of Pavement Engineering, 2019, 22(3): 1-8. DOI: 10.1080/10298436. 2019.1643022.

[6] ZENG L, XIAO L, ZHANG J, FU H Y. The role of nanotechnology in subgrade and pavement engineering: A review [J]. Journal of Nanoscience and Nanotechnology, 2020, 20(8): 4607-4618. DOI: 10.1166/jnn.2020.18491.

[7] REN D, SUN W, HUANG H, NAN J X, CHEN B. Determination of microscopic waterflooding characteristics and influence factors in ultra-low permeability sandstone reservoir [J]. Journal of Central South University, 2017, 24(9): 2134-2144. DOI: 10.1007/s11771-017-3622-6.

[8] TSANG Y W, TSANG C F. Channel model of flow through fractured media [J]. Water Resources Research, 1987, 23(3): 467-479. DOI: 10.1029/WR023i003p00467.

[9] NICHOLL M J, RAJARAM H, GLASS R J, DETWILER R L. Saturated flow in a single fracture: Evaluation of the Reynolds equation in measured aperture fields [J]. Water Resources Research, 1999, 35(11): 3361-3373. DOI: 10.1029/ 1999WR900241.

[10] WANG L, CARDENAS M B, SLOTTKE D T, KETCHAM R A, SHARP J M. Modification of the local cubic law of fracture flow for weak, inertia, tortuosity and roughness [J]. Water Resources Research, 2015, 51(4): 2064-2080. DOI: 10.1002/ 2014WR015815.

[11] GAO Q F, DONG H, HUANG R, LI Z F. Structural characteristics and hydraulic conductivity of an eluvial-colluvial gravelly soil [J]. Bulletin of Engineering Geology and the Environment, 2019, 78(7): 5011-5028. DOI: 10.1007/s10064-018-01455-1.

[12] ZHANG J, PENG J, LIU W, LU W H. Predicting resilient modulus of fine-grained subgrade soils considering relative compaction and matric suction [J]. Road Materials and Pavement Design, 2019, 8: 1-13. DOI: 10.1080/ 14680629.2019.1651756.

[13] HUANG X, ZHANG R. Catastrophe stability analysis for shallow tunnels considering settlement [J]. Journal of Central South University, 2018, 25(4): 949-960. DOI: 10.1007/ s11771-018-3796-6.

[14] TZELEPIS V, MOUTSOPOULOS K N, PAPASPYROS J N E, ABDTSIHRINTZIS V A. Experimental investigation of flow behavior in smooth and rough artificial fractures [J]. Journal of Hydrology, 2015, 521: 108-118. DOI: 10.1016/j.jhydrol. 2014.11.054.

[15] RAU G C, ANDERSEN M S, ACWORTH R I. Experimental investigation of the thermal dispersivity term and its significance in the heat transport equation for flow in sediments [J]. Water Resources Research, 2012, 48(3): 3454-3467. DOI: 10.1029/2011WR011038.

[16] SHARMEEN R, ILLMAN W A, BERG S J, YEH T J, PARK Y J, SUDICK E A, ANDO K. Transient hydraulic tomography in a fractured dolostone: Laboratory rock block experiments [J]. Water Resources Research, 2012, 48(10): 1075-1086. DOI: 10.1029/2012WR012216.

[17] QIAN J, ZHAN H, ZHAO W, SUN F G. Experimental study of turbulent unconfined groundwater flow in a single fracture [J]. Journal of Hydrology, 2005, 311(1-4): 134-142. DOI: 10.1016/j.jhydrol.2005.01.013.

[18] LIU R, LI B, JIANG Y. Critical hydraulic gradient for nonlinear flow through rock fracture networks: The roles of aperture, surface roughness, and number of intersections [J]. Advances in Water Resources, 2016, 88: 53-65. DOI: 10.1016/j.advwatres.2015.12.002.

[19] LIN H, DENG J G, LIU W, XU J, LIU H L. Numerical simulation of hydraulic fracture propagation in weakly consolidated sandstone reservoirs [J]. Journal of Central South University, 2018, 25(12): 2944-2952. DOI: 10.1007/s11771-018- 3964-8.

[20] VITEL M, ROUABHI A, TIJANI M, GUERIN F. Modeling heat and mass transfer during ground freezing subjected to high seepage velocities [J]. Computers and Geotechnics, 2016, 73: 1-15. DOI: 10.1016/j.compgeo.2015.11.014.

[21] GUO Ai-guo, ZHAI Ping-yi. Correction of the influence of rubber film restraint in triaxial compression test [J]. Rock and Soil Mechanics, 2002(4): 442-445. DOI: 10.16285/ j.rsm.2002.04.012. (in Chinese)

[22] XIONG Feng, SUN Wei, JIANG Qing-hui, YE Zu-yang, XUE Dao-rui, LIU Ru-yan. A low-speed nonlinear seepage model for rough rock fissures and its experimental verification [J]. Rock and Soil Mechanics, 2018, 39(9): 3294-3302, 3312. DOI: 10.16285/ j.rsm.2016.2623. (in Chinese)

[23] CHENG W, LIU Z, YANG H, WANG W Y. Non-linear seepage characteristics and influential factors of water injection in gassy seams [J]. Experimental Thermal and Fluid Science, 2018, 91(2): 41-53. DOI: 10.1016/j.expthermflusci. 2017. 10.002.

[24] XIAO Y, DESAI C S, DAOUADJI A, STUEDLEIN A W, LIU H, ABUELNAGA, H. Grain crushing in geoscience materials-Key issues on crushing measure, testing and modelling: Review and preface[J]. Geoscience Frontiers, 2020, 11(2): 363-374. DOI: 10.1016/j.gsf.2019.11.006.

(Edited by HE Yun-bin)

中文导读

不同围压和温度下粉砂质粉质泥岩裂隙的渗流特性

摘要：为研究围压和温度对粉砂质泥岩裂隙渗流特性的影响，采用自行研发的裂隙渗流实验系统对裂隙粉质泥岩进行渗流试验，探讨了不同因素对渗透系数的影响。结果表明：围压的增大会导致渗透系数逐渐减小，该过程分为快速减小和缓慢减小两个阶段。其中，快速减小阶段对应的围压小于30 kPa；缓慢降低阶段对应的稳压则大于30 kPa。温度对裂隙渗透系数的影响与围压不同，温度升高将导致渗透系数增加。此外，裂隙面粗糙度也在一定程度上影响渗透系数的变化，但这种变化受到围压的影响较大，当围压大于50 kPa时，这种影响逐渐消失。可以看出，在以上三种因素中，围压的变化是影响裂缝渗透系数改变的主要因素，且围压和裂隙渗透系数之间的关系可以通过指数函数来量化。

关键词：粉质泥岩；渗流特性；围压；温度；渗透系数

Foundation item: Projects(51838001, 51878070, 51908073, 51908069) supported by the National Natural Science Foundation of China; Project(2019SK2171) supported by the Key Research and Development Program of Hunan Province, China; Project(kq1905043) supported by the Training Program for Excellent Young Innovators of Changsha, China; Project(2019IC04) supported by Double First-class Scientific Research International Cooperation Expansion Project of Changsha University of Science & Technology, China; Project(CX20200811) supported by Postgraduate Research and Innovation Key Project of Hunan Province, China.

Received date: 2020-03-27; Accepted date: 2020-04-16

Corresponding author: ZENG Ling, PhD, Associate Professor; Tel: +86-731-85256006; E-mail: zl001@csust.edu.cn; ORCID: 0000- 0001-8167-1049