等距变形体的矩不变量构造方法

周建存^1,2，常亮²，郭克华²

(1. 湖南城市学院 信息科学与工程学院，湖南 益阳，413000；

2. 中南大学 信息科学与工程学院，湖南 长沙，410083)

摘要：针对变形体由于形状的变化，其不变量的构造在模式识别领域较困难等问题，对等距变形体的识别问题进行研究，提出一种等距变形体的矩不变量构造方法。首先利用三角网格上的快速行进算法来构造特征矩阵，使得点对之间的测地距离得以保存；然后，对特征矩阵进行归一化，保证同一目标特征矩阵的不变性；最后，构造矩不变量对归一化特征矩阵进行特征提取，并对该矩不变量的平移、尺度和旋转不变性进行证明。研究结果表明：与传统方法相比，该类不变量在不降低识别效果的前提下，运算复杂度较低，并对噪声具有较强的鲁棒性。

关键词：等距变形；矩不变量；微分几何；模式识别

中图分类号：TP391          文献标志码：A         文章编号：1672-7207(2012)08-3099-05

Construction of moment invariants for isometric deformed object

ZHOU Jian-cun^1,2, CHANG Liang², GUO Ke-hua²

(1. School of Information Science and Engineering, Hunan City University, Yiyang 413000, China;

2. School of Information Science and Engineering,Central South University, Changsha 410083, China)

Abstract: Based on the fact that the construction of invariants for isometric deformed object is difficult to research the pattern recognition, a new construction method of moment invariants for isometric deformed object was proposed to study the isometric deformed object recognition problem. First, fast marching method on triangulate domains was employed to compute the signature matrix to store the geodesic distance of every point pair. Secondly, the invariance was guaranteed by the normalization procedure on the signature matrices. Then, the moment invariants were constructed based on the normalized signature matrix, and the invariance of translation, scale and rotation were proved. The results show that the proposed method has less calculation complexity and stronger good noise robustness compared to traditional approach without reducing the recognition rate.

Key words: isometric deformation; moment invariants; differential geometry; pattern recognition

近年来，变形体的识别问题在模式识别领域内越来越多地受到关注。变形体识别具有较为广阔的应用前景，如表情无关的三维人脸识别^[1-2]、三维纹理分  析^[3]和医学图像处理^[4-5]中很多技术都与变形体的识别有关。在变形体识别问题中，目标发生变形，特征难以提取，该问题成为模式识别领域内难点。传统的三维目标识别方法^[6]主要针对刚体进行识别，难以处理目标变形情况下的问题。目前，对变形体的研究主要集中在变形过程的计算机仿真，而对变形体匹配的研究很少。由于对任意情况下变形体进行识别比较困难，因此，目前的研究主要集中在具有条件限制下的变形体识别。在变形体识别的研究中，目前热门的研究是对等距变形体进行识别。等距变形的定义如下：给定为二维欧几里德流形S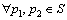，, 为这2点之间的测地距离。对于变换，若  满足：

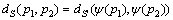        (1)

则称变换ψ为等距变换，此变换下的变形称为等距变形。可见：等距曲面变形后，表面相应点之间的测地距离保持不变。因此，测地距离是等距变形体的基本特征，测地距离的不变性成为等距变形体识别的关键。在已有的等距变形体的研究中，最传统的方法是将变形体划分为几个未变形的部分，然后，基于这些部分分别进行识别。Bloomenthal等^[7-8]基于这种思想，构造了变形体的骨架，在具有关节结构的变形体识别中，取得了较好效果。但是，这种方法无法针对目标的任意等距变形进行识别。一些研究者提出了基于几何统计方法的变形体识别策略。Aherne等^[9-11]首先计算目标表面一些微分几何量，然后构造直方图进行统计，将这种方法在三角网格上得到应用。Osada等^[12]则通过评估目标表面任意点的某个欧几里德值(如距离) 的分布函数来计算目标的统计特征。这些方法比较简单，但是，只对小范围内的变形具有鲁棒性。目前比较好的一种等距变形体识别方法是将等距曲面等价映射成1个高维刚体，任意适用于刚体匹配的算法都能起作用，如Elad等^[13]将这种方法应用到表情无关的三维人脸识别中，取得了较好效果，但是，该类算法运算复杂度较高。为此，本文作者针对等距变形这种特殊的变形体识别问题进行研究，提出该变形情况下目标识别的新方法。该方法通过构造不变量来描述等距变形体的特征，首先利用测地距离的概念构造出等距变形体的特征矩阵，然后对特征矩阵进行归一化，最后利用矩不变量对归一化特征矩阵的特征进行提取，构造出相应的矩不变量，并对该类矩不变量的平移、尺度和旋转不变性进行证明。

1  等距变形体的特征数据存储

1.1  测地距离的获取

等距曲面变形之后，表面相应点之间的测地距离保持不变。因此，测地距离是等距变形体的基本特征，可以通过计算曲面上任意2点之间的测地距离来提取不变量。

对于测地距离的获取，Sethian^[14]提出了基于矩形网格的测地距离计算方法即矩形网格上的快速行进法，Kimmel等^[15]将此方法进行改进，提出了三角网格下的快速行进法。对于含有n个顶点的曲面，这种方法能够计算任意顶点和其余各点之间的测地距离，运算复杂度为O(n)。通过计算每个顶点和其他顶点之间的测地距离，可以在O(n²)运算时间内构造1个测地距离矩阵。

1.2  特征矩阵的构造

利用三角网格下的快速行进法算法可以计算网格曲面上任意2点之间的测地距离，构造测地距离矩阵。该矩阵具有如下特征：对于具有n个顶点的等距曲面，此矩阵是n×n的对称矩阵，对角线上的元素为0。为了表述方便，可将此测地距离矩阵，确定为等距曲面的特征矩阵(S_M)，满足：

           (2)

其中：d_S(p_i，p_j)表示曲面S上顶点p_i和p_j之间的测地距离，此距离由三角网格下的快速行进法算法求出。

1.3  特征矩阵的归一化

构造出特征矩阵后，目标之间的匹配转化为特征矩阵之间的匹配。但是，由于曲面上像素点提取的顺序是任意的，所以，同一个曲面可能构造出不同的特征矩阵。这些特征矩阵对应着一些同构的带权图，若直接针对特征矩阵进行匹配，则其复杂度等价于同构图的匹配，运算时间为O(n!)。所以，必须对特征矩阵进行归一化，以保证同一个目标得到的是同一个特征矩阵。

归一化的目的是调整顶点的顺序。实际上，顶点v_i和v_j的调换将导致特征矩阵中第i行与第j行、第i列与第j列之间的调换。这里需要对特征矩阵中的顶点进行排序，以保证特征矩阵的唯一性。

该算法的基本思想是：基于每个顶点的可量化特征，将顶点按升序排列，本算法中选取顶点的均值和方差进行计算。步骤如下。

首先，计算每个顶点的均值和方差：

        (3)

其中：1≤i≤n；n为顶点个数；S_M为特征矩阵。

其次，构造向量K来存储特征矩阵中每一行在归一化特征矩阵中的位置。K初始化为零向量，K(i)通过以下准则确定：

K(i)=n′{(m_j，v_j)}，1≤j≤n         (4)

其中：n′为示集合的元素个数；(m_j，v_j)须满足如下    条件：

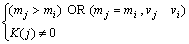       (5)

对于K(i)的构造，实际上基于每个顶点的均值和方差，将顶点按升序进行排列。而对特征矩阵中的顶点进行的排序，可以保证特征矩阵的唯一性。

然后，构建变换矩阵T来存储顶点顺序的调整情况，T为1个n×n矩阵，满足：

T(i，K[i])=1，1≤i≤n          (6)

T中其他元素为0。

最后，构造归一化后的特征矩阵N_S。该矩阵可通过下式计算：

N_S=T(S_M)T′               (7)

其中：S_M为等距曲面的特征矩阵；T′为矩阵T的转置。

综上所述，归一化特征矩阵的构造算法可以描述如下。

Step 1: 利用式(3)计算每个顶点的均值和方差。

Step 2：基于Step 1中计算的均值和方差，根据式(4)创建向量K(i)，计算每个顶点在归一化矩阵中的位置。

Step 3：基于Step 2中计算的个顶点对应的K(i)，根据式(6)构建变换矩阵T，确定对特征矩阵进行归一化的变换矩阵。

Step 4：利用式(7)，根据Step 3中计算的变换矩阵，对特征矩阵进行变换，计算出归一化特征矩阵N_S。

在以上的算法中，计算每个顶点的均值和方差，运算时间为O(n²)；利用快速排序算法，运算时间为O(nlgn)；在Step 3中，变换矩阵T的行向量和列向量都是单位向量，所以，N_S的每行能够根据变换矩阵中1的位置从S_M中提取，其运算复杂度为O(n²)。综上所述，归一化步骤的运算复杂度为O(n²)。

2  等距变形体的变形矩及其性质

归一化特征矩阵的特征可以由许多方法来提取，如傅里叶描述子、矩特征等。本文将对矩不变量进行扩展，以提取N_S的特征。

对于归一化特征矩阵，其p+q阶中心矩定义如下：

 (8)

其中：N为自然数集合。x₀和y₀为归一化特征矩阵的质心坐标，满足：

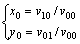              (9)

显然，由于对特征矩阵进行了归一化，该矩阵中顶点的顺序进行了调整，中心矩v_pq具备了平移不   变性。

为保证尺度变换下的不变性，需要对中心矩进行归一化，为此，构造出归一化的中心矩μ_pq：

           (10)

根据已经构造出来的归一化的中心矩μ_pq，进一步构造2个针对等距变形体的变形矩：

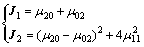         (11)

要使全速变形矩得到应用，必须具有不变性。对于前面秘构造的变形矩，下面从平移、尺度和旋转3个方面阐述其不变性质。

(1) 平移不变性。由于归一化特征矩阵中顶点的顺序进行了调整，中心矩v_pq具备了平移不变性，因此，根据式(10)构造的归一化的中心矩μ_pq也具有平移不变性。由此可见：式(11)构造出来的变形矩也具有平移不变性。

(2) 尺度不变性。设目标边界Σ为光滑的空间曲面，坐标x，y和z缩放同一因子k(k＞0)，此时，曲面上各点的坐标也将缩放因子k，特征矩阵S_M和归一化特征矩阵N_S中的元素也将缩放因子k；但是，由于式(10)中对v_pq进行了处理，其分母也是以因子k进行缩放，因此，u_pq具有尺度不变性，由式(11)构造的变形矩也具有平移不变性。

需指出的是：旋转变换不会改变测地距离的值。由于归一化特征矩阵中顶点的顺序进行了调整，因此，旋转变换只会改变特征矩阵中顶点的顺序，但不会改变归一化特征矩阵。因此，式(11)构造的变形矩具有旋转不变性。

3  实验结果和复杂度分析

因为上述理论是基于三维变形曲面的，所以，必须首先获取图像，然后构造三角网格。目前，对于三维目标图像的数据获取一般采用2种方法：(1) 由于二维图像的存储比较方便，可以通过从二维图像进行三维建模来获取三维数据；(2) 直接使用可以获取三维位置信息的工具，如三维扫描仪等。在实验中，选取几个比较典型的三维物体来进行验证。

3.1  本文方法与传统方法计算复杂度的比较

利用一些三维图像测试本文算法的分类效果。变形体研究目前还没有公认的数据库，为此建立1个包含20个目标的数据库(见图1)。在这20个目标中，有些目标具有相似之处。为了对效果进行对比，将一些传统方法应用到分类过程之中。场景像素为450。对于数据库中的每个目标，首先计算它们的特征矩阵，然后归一化，最后计算变形矩。

图1  数据库中的20个目标

Fig.1  20 Objects in Database

为了采用更多的样本，对于每个目标，对其实施任意的等距变形、旋转和缩放变换，获得10幅图像。总数据库中有200幅三维目标图像。

首先，利用本文算法对这200个不同的样本进行分类，然后，与传统的高维映射方法进行对比。

此外，传统的高维映射方法也用于本文数据库中。用MATLAB在P IV计算机上对图1所示的三维图像，分别采用本文算法和传统的高维映射算法进行计算。这2种算法的运算时间如表1所示。

表1  2种算法的计算时间比较

Table 1  Computational time of two algorithms  ms

从表1可看出：本文算法在运算方面具有较低的运算时间，因而复杂度低。

实际上，高维映射方法是将本文的特征矩阵映射到高维空间的刚体，其过程主要利用了MDS算法。在高维映射算法中，对传统MDS算法、LSMDS算法和快速MDS算法进行比较。由于快速MDS误差率较高，最终采用LSMDS算法，其运算复杂度为O(n²×N)(N为迭代次数)，其精确度依赖于迭代次数。本文算法中，归一化特征矩阵的构造的运算时间为O(n²)，小于LSMDS算法的运算时间。此外，预处理后的目标之间的匹配还需要花额外的时间，在这一点上，这2种算法所花费时间区别不大。2种算法的计算复杂度如表2所示。

表2  2种算法的计算复杂度

Table 2 Computational complexity of two algorithm

因此，从理论上分析，本文的算法也具有较低的复杂度。

3.2  本文方法与传统方法识别率的比较

本实验中，基于样本数据库，选取图1中的3个目标进行分类。首先，对图像库中的样本进行了旋转或尺度变化，选取J₁和J₂矩不变量来进行计算。此实验中，利用一阶Minkowski距离来衡量目标之间的差别。令S和S′为2个等距变形曲面。其一阶Minkowski距离定义为：

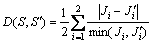        (12)

本实验中阈值取0.1。 当物体之间的距离小于或等于0.1时，就将它们归入同一类。2种算法分类效果(识别率)如表2所示。

表3  2种算法的分类效果比较

Table 3  Performance comparison of two algorithms

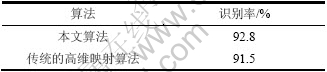
从表3可看出：本文算法在预处理方面具有较低的运算复杂度，但是，并没有降低识别率。

3.3  噪声情况下的鲁棒性比较

对数据库中的每幅图像增加高斯噪声(N(0，σ))，σ在0~2.0 mm之间变化。与传统的高维映射算法的分类效果对比结果如图2所示。

从图2可以看出：本文算法和传统算法对噪声都具有较好的鲁棒性。实际上，因为这2种方法都是基于距离进行计算的，因此，噪声对计算结果的影响不是太大。

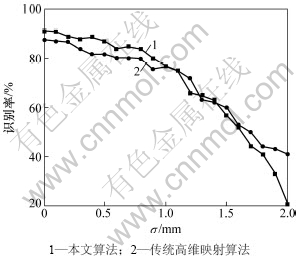
图2  高斯噪声变化时的识别效果

Fig.2  Performance comparison in gaussian noise

4  结论

(1) 针对等距变形这种特殊的变形体识别问题进行研究，提出了该变形情况下目标识别的新方法。该方法通过构造不变量来描述等距变形体的特征，首先利用测地距离的概念构造出等距变形体的特征矩阵，然后对特征矩阵进行归一化，最后利用矩不变量对归一化特征矩阵的特征进行提取，构造出相应的矩不变量，并对该类矩不变量的平移、尺度和旋转不变性进行了证明。

(2) 在不降低识别效果的前提下，本文构造的方法和传统的高维映射算法相比，不需要将三维目标映射到高维空间，具有较低的运算复杂度，并具有较强的鲁棒性。

(3)下一步工作是对有遮挡情况下的等距变形体识别问题以及任意拓扑变形情况下的目标识别问题进行研究。

参考文献：

[1] 文沁, 汪增福. 基于三维数据的人脸表情识别[J]. 计算机仿真, 2005, 22(7): 99-103.
WEN Qin, WANG Zeng-fu. Recognition of human facial expression based on 3D data[J]. Computer Simulation, 2005, 22(7): 99-103.

[2] PAN Gang, HAN Song, WU Zhao-hui, et al. Removal of 3D facial expressions: A learning-based approach[C]//2010 IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, USA, IEEE Computer Society Press, 2010: 2614-2621.

[3] Burner A, Donner R, Mayerhoefer M, et al. Texture bags: Anomaly retrieval in medical images based on local 3D-texture similarity[J]. Lecture Notes in Computer Science, 2012, 7075: 116-127.

[4] Heckela F, Konradb O, Hahna H K, et al. Interactive 3D medical image segmentation with energy-minimizing implicit functions[J]. Computers & Graphics, 2011, 35(2): 275-287.

[5] DU Xin-wei, CHE Xiang-jiu. A hierarchical approach to 3D scattered data interpolation with radial basis functions[C]//12th International Conference on Computer-Aided Design and Computer Graphics. Jinan: IEEE Computer Society Press, 2011: 262-267.

[6] Besl P J, Jain R C. Three-dimensional object recognition[J]. ACM Computing Surveys, 1985, 17(1): 75-145.

[7] Bloomenthal J, Lim C. Skeletal methods of shape manipulation[C]//Proceedings of the International Conference on Shape Modeling and Applications. Washington: IEEE Computer Society Press, 1999: 44-47.

[8] TIAN Guang-feng. Three-dimension rheological model and parameters solving for unsaturated soil[J]. Advanced Materials Research, 2012, 368: 2698-2701.

[9] Aherne F, Thacker N, Rockett P. Optimal pairwise geometric histograms[C]//Proc British Machine Vision Conference Colchester: UK, 1997: 480-490.

[10] Park S. 2DPCA-based method for place classification using range scan[J]. Electronics Letters, 2011, 47(25): 1364-1366.

[11] ZHANG Yu, QI Mei-xing, LI Shang. Palmprint recognition based on two-dimensional gabor wavelet transform and two-dimensional principal component analysis[J]. Lecture Notes in Computer Science, 2012, 6838: 405-411.

[12] Osada R, Funkhouser T,Chazelle B, et al. Shape distribution[J]. ACM Transactions on Graphics, 2000, 21(4): 807-832.

[13] Elad A, Kimmel R. On bending invariant signatures for surfaces[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(10): 1285-1295.

[14] Sethian J A. Theory, algorithms and applications of level set method for propagating interfaces[J]. Acta Numerica, 1996, 5: 309-395.

[15] Kimmel R, Sethian J A. Computing geodesic paths on manifolds[J]. Proc of National Academy of Science, 1998, 95(15): 8431-8435.

(编辑 陈灿华)

收稿日期：2011-11-12；修回日期：2012-01-25

基金项目：教育部博士点基金资助项目(20090162120069)；湖南省科技计划项目(2009FJ3016)；中央高校基本业务费青年教师助推项目(2011QNZT022)

通信作者：周建存(1977-)，男，湖南宁乡人，讲师，从事计算机网络研究；电话：18684788345；E-mail：zhoujiancun101@126.com