基于改进型遗传算法的存储子系统动态负载均衡

倪云竹，李志蜀，胡大裟

(四川大学 计算机学院，四川 成都，610064)

摘要：衡量一个存储子系统性能的主要指标有容量、响应时间和吞吐量，而请求内在的并行性和负载均衡最终共同决定了其响应时间和吞吐量。为全面提高其性能，通过对磁盘阵列结构的研究，首先构建一个由多个磁盘阵列组成的存储子系统，并在此基础上提出一种新的动态测量磁盘阵列负载变化的方法以及磁盘阵列之间负载不均的判断标准。此外，针对磁盘阵列之间的负载不均问题提出一种基于改进型遗传算法来实现动态负载均衡的方法，并通过仿真实验证明该算法正确有效。从而从多方面改善存储子系统的容量、响应时间和吞吐量。

关键词：磁盘阵列；分条；动态负载均衡；遗传算法；蚁群算法

中图分类号：TP333          文献标志码：A         文章编号：1672-7207(2013)08-3186-10

Solution of dynamic load balancing in storage subsystem based on improved genetic algorithm

NI Yunzhu, LI Zhishu, HU Dasha

(College of Computer, Sichuan University, Chengdu 610064, China)

Abstract: The main performance indexes of the storage subsystem are capacity, response time and throughput. The request’s parallelism and the load balance in storage subsystem determine the response time and throughput. In order to improve these performances, we build a storage subsystem consisted of more disk arrays, and present a new method for dynamic measurement of the load’s variation in disk arrays and a new judgment criterion of load imbalance between the disk arrays. Moreover, to solve the dynamic load imbalance between the disk arrays, we present a new scheme based on an improved Genetic Algorithm, and computer simulations show that the proposed algorithm is correct and effective. Consequently, the storage subsystem’s capacity, response time and throughput can be improved in many ways.

Key words: disk array; striping; dynamic load balancing; genetic algorithm; ant colony algorithm

随着计算机系统中各部件性能的快速发展，对存储子系统的性能和可靠性的要求也逐渐提高。于是，各种新的存储技术应运而生。具有多个磁盘的磁盘阵列是目前能够提供最高访问速度和海量存储空间的外置存储设备，它所具备的优点使其早已成为了大中型服务器以及高性能计算机所使用的主流存储系统。但是，对于绝大部分磁盘阵列产品来说，其扩充能力都是受到限制的。此外，由于不同RAID(redundant arrays of inexpensive disks)级别的特点不同，其应用场合也是不同的。因此，在一些对I/O吞吐量和读写速度要求较高，并要求提供多种不同服务的实际应用中，仅仅由若干个磁盘组成的、采用同一种RAID级别的一个磁盘阵列往往是不能满足其需求的。除此以外，衡量一个磁盘阵列性能的主要指标有平均响应时间和总的系统吞吐量^[1]。而请求内在的并行性和负载均衡最终共同决定了磁盘阵列的响应速度和吞吐量。当一个磁盘阵列处理一个应用时，该磁盘阵列所表现出的I/O并行的潜力水平依赖于该应用数据的分布。一个文件的划分决定了处理该文件的单个请求的并行性水平，而文件的分块在磁盘上的分配决定了磁盘阵列的负载均衡。所谓磁盘负载不均，是指当一个存储子系统中一些磁盘驱动器所接受的数据访问量远大于其他磁盘驱动器时，就称之为磁盘负载不均衡。而目前提高存储子系统性能的最大障碍就是负载不均衡或称为磁盘偏移^[2]。目前主要有2种技术解决磁盘负载不均：动态数据存放技术和磁盘分条技术^[3]。然而，仅仅使用动态数据存放技术是不够的，因为它不仅需要花费大量的时间和精力，并且最终还往往无法提供一个可靠的解决方法^[3]。而存储系统中磁盘驱动器个数的不断增加使得采用动态数据存放技术实现负载均衡愈发困难。磁盘分条技术^[4-5]在解决负载不均问题上虽然优于动态数据存放技术，但是，它仅考虑静态的负载均衡，即对有关工作量的访问模式是事先完全清楚的。文献[6]提出了一种在磁盘阵列中实现数据分配和动态负载均衡的自适应方法，其基本思想是分配并合理地迁移数据使得磁盘阵列中的磁盘负载量变化减小，但这要求其负载量与具有稳态访问特征的时间间隔的长度成比例，并且对它的访问具有周期性变化的特征和可预测性。文献[7]还提出一种基于遗传算法的物理磁盘间负载均衡方法，以提高磁盘阵列的吞吐量。不过，该方法仅从存储设备的角度来考虑，而不是从应用程序或文件的角度来考虑的，并且其只限于考虑静态数据的分配。因此，基于上述分析，并参考了文献[8]等诸多文献后，本文作者首先构建了一个由多个磁盘阵列组成的存储子系统，并在此基础上提出了一种新的动态测量磁盘阵列负载变化的方法以及磁盘阵列之间负载不均的判断标准。此外，针对磁盘阵列之间的负载不均问题提出了一种基于改进型遗传算法来实现动态负载均衡的方法。

1  构建磁盘阵列结构

在一些对I/O吞吐量和读写速度要求较高的实际应用中，由若干个磁盘组成的一个磁盘阵列所提供的速度往往是不够的。因此，在本文中建立了一个由多个磁盘阵列组成的存储子系统。该存储子系统可根据所提供的应用不同划分成不同的磁盘阵列组，其中每组可根据具体应用来确定采用的RAID级别以及所需的磁盘阵列个数。换句话说既可以单由一个磁盘阵列构成一组，为某一种具体应用服务；也可以由多个磁盘阵列构成一组共同为同一种应用服务。若是由多个磁盘阵列共同为同一种应用服务，则要求该组中的磁盘阵列均采用相同的RAID级别。其结构如图1所示。假设整个存储子系统共划分为W个磁盘阵列组，其中第1组共有N个磁盘阵列，那么这N个磁盘阵列均采用统一RAID(如RAID0)结构，它们分别定义为P_i，i=1，2，…，N。而其余组的磁盘阵列可根据各自的应用需求选择不同的RAID结构。这样，不但能够同时满足多种不同应用需求，并且当多个磁盘阵列组成一组同时为一种应用服务时，由于每个磁盘阵列都有各自的I/O通道，因此可以同时响应多个访问请求，提高了存储子系统的并发性，从而实现较高的I/O吞吐量和读写速度。

2  数据的划分与分配

图1所示为文件f₁在第1个磁盘阵列组中的分配。在该磁盘阵列组中，一个文件只能存放到其中一个磁盘阵列中。确切地说，就是先确定该文件存放在哪一组磁盘阵列，然后采用分条技术，将该文件划分成若干块(如：f_1-1，f_1-2，f_1-3，f_1-4)，并把这些块分别存放在同一个磁盘阵列(如：P₁)中不同的磁盘上。而在分条技术中，分条单元是减少单个请求的服务时间或提高多个请求的吞吐量的一个非常重要的参数，其大小需要正确选择^{[2, 9]}。并且，Gradecki等^[10]提出分条单元的大小应该灵活选取。因此，在本研究的前期工作中，提出了一种新的选择合适的分条单元的方法^[11]。通过该方法，能够实现磁盘间较好的负载均衡以及获得较优的响应时间。

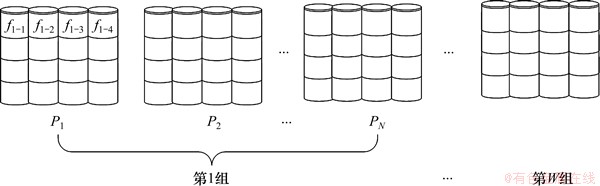
图1  存储子系统结构

Fig. 1  Storage subsystem structure

然而，由于对不同文件的访问请求个数是不同的，并且对同一文件的访问请求数也会随时间的变化而变化，因此，使用分条技术仅仅能实现一个磁盘阵列中各磁盘之间的负载均衡。究竟将文件放入哪一个磁盘阵列中，需要进行选择和不断地调整。一旦存放不当，可能会导致磁盘阵列之间的负载不均衡。因此，在本文所采用的磁盘阵列结构中，即使使用了分条技术，也需要考虑采取一定的方法实现磁盘阵列之间的负载均衡。

3  建立基于分条技术的磁盘阵列模型

3.1  建立磁盘阵列映射关系

图2不仅表示了磁盘阵列组的组成结构，还显示了物理磁盘阵列和逻辑磁盘之间的映射关系。其中涉及到2个概念：物理磁盘阵列和逻辑磁盘。物理磁盘阵列即前面提到的同一组中的磁盘阵列。由物理磁盘阵列组成的集合表示为P={P₁，P₂，…，P_N}，N表示磁盘阵列个数，P_i(1≤i≤N)表示第i号磁盘阵列。而逻辑磁盘是指需要存放到磁盘阵列上的文件，逻辑磁盘与物理磁盘阵列之间的对应关系称之为映射。在本文中，将映射到物理磁盘阵列上的每一个文件看作是一个逻辑磁盘，并对其进行统一编号，产生一个具有M个逻辑磁盘的集合L={L₁，L₂，…，L_M}，其中M 表示逻辑磁盘的个数，L_i(1≤i≤M)为第i号逻辑磁盘。为简化算法，假定N能够被M整除。当每一个逻辑磁盘映射到某一物理磁盘阵列上时，即将逻辑磁盘上的数据进行划分，并采用分条方式分配到该磁盘阵列中的多个磁盘上。

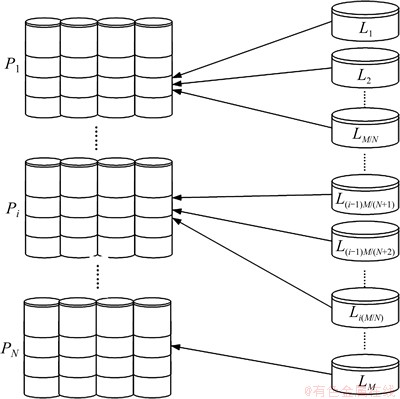
图2  物理磁盘阵列和逻辑磁盘之间的映射关系^[12-13]

Fig. 2  Mapping relationship between physic disk arrays and logic disks

3.2  测量磁盘阵列热度

物理磁盘阵列的热度(也称为负载)是由映射到它上面的逻辑磁盘的热度相加得到。而逻辑磁盘即文件的热度定义为其单位时间内被访问的请求个数^[6]。

对文件热度的测量，常见的方法是在最近的时间T内追踪测量访问某文件的请求的个数，从而确定该文件的热度^[5]。其中T是一个全局可调参数。但是这种方法存在的一个问题就是它对访问热度高的(可称之为：“热的”)文件和热度低的(可称之为：“冷的”)文件的追踪测量无法同时都具有相同的灵敏度。因为对于热的文件来说，需要时间段相对较短，从而确保能充分测量到热度的变化；而相反的，对于冷的文件则需要时间段相对较长，以确保能够观测到足够数量的访问请求以消除由于随机波动造成的测量数据的局部性或不完整性。

由此，Scheuermann等^[5-6]提出了一种通过使用“移动窗口”来测量文件块热度的方法。这种热度评估方法对文件块热度的突然增加非常灵敏，但是当一个文件块的热度突然下降，其热度评估就会显得非常迟缓。举一个极端的例子，突然间停止对一个热的文件块的任何访问，那么在这种情况下，它会继续保持该文件块之前评估的热度，就如同暂时还没有新的访问请求到达。这显然与实际情况是不相符的。

在本文中，对上述方法做了一定的改进，对文件的热度主要采用动态测量的方法。其具体实现如下：

(1) 假设某文件块被访问的时间点分别表示为：t₁，t₂，…，t_i，…。设置访问请求间最大时间间隔T_s，其值可根据实际应用的访问频率进行设置。通常情况下，T_s≥(t_i-t_i-1)。

(2) 对该文件的初始请求时间记录为空，请求数计数器清零。当该文件有一新请求到达时，将其到达时间记录下来，同时请求数计数器加1。按上述方法依次记录下h个请求的到达时间，直到请求数计数器的值为h。

(3) 当请求数计数器的值为h时，根据请求时间记录中h个请求各自的到达时间，采用如下文件热度计算式(1)计算出文件f_x当前的热度。

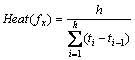          (1)

其中：h是微调参数，其取值可根据具体应用和访问模式进行设定。

(4) 若在最大时间间隔T_s内，有一个新请求到达，记录下该请求的到达时间，同时删除记录中最早一项时间记录，即保持时间记录中始终保持h个请求的到达时间。并且采用式(1)更新文件f_x的热度。而反之，若在最大时间间隔T_s内，无新请求到达，则根据之前记录中的h个请求的到达时间采用如下文件热度计算式(2)更新文件f_x的热度。

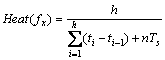          (2)

其中：n为最大时间间隔T_s的个数，初始值为1，每间隔一个T_s，n自动加1。

(5) 重复第(4)步。

在本文中，由于将需要存放到物理磁盘阵列上的每一个文件看作是一个逻辑磁盘，因此，每一个逻辑磁盘的热度即为该文件的热度，它会随着访问请求到达的变化以及时间的变化而变化。但是，在实际应用环境中，由于很多文件的访问请求的到达率在短时间会保持大体一致。因此，其热度在短期内变换不大，而是呈现出周期性变化的特征。所以，虽然可根据上述热度计算方法得到不同请求到达时的时间和对应逻辑磁盘的热度。但是，每次当一个新的请求到达时就读取一次逻辑磁盘的热度是没有必要的。

在本文中，读取逻辑磁盘热度的时间和方法是：首先根据实际应用中逻辑磁盘热度的周期性变化特征，假设周期T为最佳时间跨度。然后，根据逻辑磁盘的热度变化规律所产生的不同热度所在的时间点再将周期T细分为n个时间段，定义为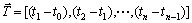：。最后在每个时间段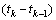结束时对各逻辑磁盘热度重新进行一次读取：

若t_h≤t_k＜t_h+1 且t_k＜t_h+T_s，则逻辑磁盘L_i 在时间段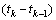中的热度可表示为：

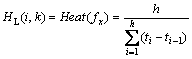        (3)

若t_h+T_s≤t_k＜t_h+1，则逻辑磁盘L_i 在时间段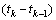中的热度可表示为：

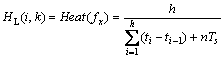     (4)

若已有新请求h+1到达，即t_k≥t_h+1，则用t_h+1替换掉t_h，根据实际情况选择第(1)项或第(2)项执行。

由此可得出在周期T中逻辑磁盘L_i的平均热度为：

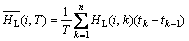       (5)

根据图2所示的物理磁盘阵列与逻辑磁盘的映射关系可知：物理磁盘阵列的热度为映射到该磁盘阵列上的所有逻辑磁盘的热度之和，因此某一物理磁盘阵列P_i在周期T中的热度为：

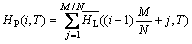         (6)

通常一个文件可能被动态地分配或删除，并且对同一文件的访问请求数也会随时间的变化而变化，从而导致文件所在的磁盘阵列热度发生变化。因此，即使开始时磁盘阵列之间的负载是均衡的，但是之后就不一定了。所以有必要在数据分配后的每隔一定时间判断磁盘阵列之间是否存在负载不均，若存在，则要进行负载调整以实现磁盘阵列之间的负载均衡。

在本文中，设定磁盘阵列之间是否存在负载不均的判断标准如下：

整个磁盘阵列组在时间T内的总的热度变化值(相对于平均值的均方差)表示为：

       (7)

其中：

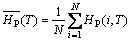          (8)

当σ(T)满足预先设定的某一约束值时，表示当前磁盘阵列之间是负载均衡的；反之，表示磁盘阵列之间存在负载不均，就需要进行负载调整。

3.3  数据模型的定义

通过前面的分析，可定义如下数据模型：

(1) 由物理磁盘组成的磁盘阵列的集合定义为P={P₁，P₂，…，P_N}，其中N表示磁盘阵列个数，P_i(1≤i≤N)为第i号磁盘阵列。

(2) 表示数据文件的逻辑磁盘的集合定义为L={L₁，L₂，…，L_M}，其中M表示逻辑磁盘的个数，L_i(1≤i≤M)为第i号逻辑磁盘。

(3) 各个逻辑磁盘在T时间段的热度的集合定义为：

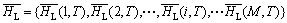
其中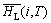：表示第i个逻辑磁盘在T时间段的平均热度。

各个磁盘阵列在T时间段的热度(负载)的集合定义为：

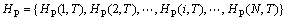
其中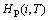：表示第i个物理磁盘阵列在T时间段的热度，其值为所有映射到磁盘阵列P_i上的逻辑磁盘的热度之和。

某种映射方案S _k下，物理磁盘阵列组在T时间段总的热度变化值定义为：

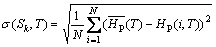       (9)

其中：S _k表示一种映射方案，

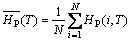            (10)

本文的目标就是寻找一种解S_k，使得σ(S_k, T)满足预定的热度约束条件，从而实现磁盘阵列的负载均衡。对于解S_k，可以通过改进型遗传算法进行搜索。

4  用改进型遗传算法实现磁盘阵列负载均衡

很显然，无论文件在存放之前是否被划分成数据块，其在磁盘阵列上的分布决定了磁盘阵列之间的负载均衡。而数据在磁盘阵列上的分配问题近似于分布式系统中文件的分布问题，属于NP-难问题。因此可行的解决方案必须是基于启发式的^[5]。

遗传算法(genetic algorithm，简称GA)一直以来被认为是解决NP-难问题最有效的方法之一。它具有大范围的快速全局搜索能力，但当求解到一定程度时，往往需要做大量的冗余迭代，并且对系统中的反馈信息利用不够，因此求解效率低。蚁群算法(ant colony algorithm，简称ACA)是一种新型的仿生优化算法，它主要通过模拟蚂蚁群体觅食的过程来解决一些NP-难组合优化问题^[14]。但通常由于初期信息素匮乏，一般需要较长的搜索时间，容易出现停滞现象^[14]。在本文中，将蚁群算法的正反馈收敛机制融入到遗传算法中，提出了一种新的改进型遗传算法(improved genetic algorithm，简称I-GA)。初期采用遗传算法过程生成信息素分布，后期利用蚁群算法正反馈求精确解，优势互补。

4.1  编码表示

对于本文所提出的磁盘阵列数据模型，为更好地表现物理磁盘阵列与逻辑磁盘之间一对多的映射关系，最好的表示方法不是二进制编码而应该是树结构。因此本文采用了树结构来表示染色体。即每一种映射方案都可表示为一个3层的树，其中，第1层只有1个结点即根结点，由系统定义；第2层共有N个结点，分别代表N个物理磁盘阵列；第3层共有M个结点，分别代表M个逻辑磁盘。

4.2  确定适应度函数

在本算法中，适应度函数是用来衡量种群中个体优劣的标准，它将直接反映个体的性能。根据适应度函数值，决定某些个体是繁殖还是消亡。本文算法的适应度函数定义为：

       (11)

其中：A为加权系数，它的值可根据具体应用来设定；σ₀表示实现磁盘阵列负载均衡所能允许的热度变化值约束，该值可以根据具体应用预先设定；函数σ(S_k, T)表示磁盘阵列组在T时间段内实际的热度变化值，该函数在前面已经详细介绍过。

4.3  生成初始种群

4.3.1  初始化种群

对种群的初始化，本文主要采取生成树的方法。首先假设每棵树代表一个个体，对一棵树的定义如下：

(1) 该树是由物理磁盘阵列和逻辑磁盘2个集合中的元素构成的生成树。

(2) 该树的根是源结点，预先设定，非任一磁盘结点。

(3) 所有物理磁盘阵列结点和逻辑磁盘结点都在树中。

(4) 所有叶子结点都是逻辑磁盘结点。

生成一棵树的原则是使该树能满足给定的负载均衡条件或使它能够产生出较优良的后代，这就要求它本身也是较优良的个体。因此生成物理磁盘阵列结点与逻辑磁盘结点之间的链路时，可按照以下分配方法进行分配：

(1) 设定与每个物理磁盘阵列相映射的逻辑磁盘个数为q(q = M/N)。

(2) 按照逻辑磁盘热度集合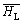中各磁盘的平均热度计算出各逻辑磁盘的选择概率p_i 。p_i 定义为：

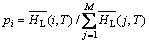          (12)

(3) 根据概率p_i选出逻辑磁盘L_i，将其分配给各物理磁盘阵列结点P₁~P_N中当前热度值(即当前所映射的逻辑磁盘的热度之和)最小的结点以形成初始生成树的叶子结点。这样可使具有较大热度的逻辑磁盘被选中的概率较大，同时也使具有较小热度的逻辑磁盘也有被选中的机会。

4.3.2  解空间的初始标定

在I-GA中，可将整个解空间划分成若干个子空间。解空间可以表示成SPACE={1，2，…，k，…，P_size }，其中，k 表示第 k 个子空间，而P_size表示种群大小。每一个初始个体就是对应子空间中的一个解。可作如下定义：

在每个子空间k中，又划分成不同代，每一代中包含一个解。子空间k中的这些解可表示为{S_k (1)，S_k (2)，…，S_k (t)，…}，其中，S_k (t) 表示在第t代中的个体解S_k。

每一个子空间都由一个信息量^[14]Ph标定，各个子空间信息量的初始值由其对应的初始个体的适应度确定。其定义如下：

    (13)

其中：Ph_k(0)表示子空间k的初始信息量；f(S_k(0)) 为初始个体S_k的适应度；C₁，C₂和C₃ 为根据具体问题而设定的正常数，且C₂＞C₃。

4.4  制定选择策略

选择操作的主要目的是为了避免基因缺失，以提高全局收敛性和计算效率。选择策略对算法的性能会产生重要的影响。不同的选择策略会导致不同的选择压力，较大的选择压力使最优个体具有较高的复制数目，从而加快算法的收敛速度，但是也容易导致过早收敛。反之，较小的选择压力通常能保持群体的多样性，从而增大算法收敛到全局最优的概率，但其收敛速度一般较慢^[15]。

本文制定的选择操作的基本思想是：第t代中的个体S_k被选中并被复制到下一代的概率是由其个体适应度值和所对应子空间信息量的函数来决定的。其选择概率定义为：

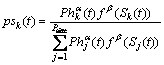        (14)

其中：f(S_k(t))为第t代中个体S_k的适应度；Ph_k(t)为子空间k在t代中标定的信息量；P_size为种群规模；α为信息启发因子；β为期望启发因子；α和β分别表示了信息量和适应度在决定蚂蚁行为上各自的影响力。

4.5  杂交操作

在本文采用树型编码的算法中，要保证后代的染色体具有合法性，其杂交方式不能采用简单交换部分基因的方式，必须根据具体问题设计专门的杂交算子。

本文设计的杂交过程如下：

(1) 按本文提出的选择策略从种群中选择2个父代个体，表示为T₁和T₂。

(2) 将2个父代个体T₁和T₂合并，合并后将得到一个新的图。由于该图中包含了2个父代个体的所有链路和结点，因此原来的叶子结点有的将不止连接一个二层结点。

(3) 根据合并的图生成一个新的个体树T₀，T₀中去掉了具有2条链路的叶子结点及与它相连的链路，这样T₀仍为一棵树。

(4) 根据式(12)中所提出的选择概率计算方法，将步骤(3)中去掉的叶子结点按照各磁盘的热度计算出各逻辑磁盘的选择概率p_i。

(5) 将去掉的叶子结点按概率p_i分配给结点P₁~P_N中当前热度最小的结点作为其叶子结点，直到将所有去掉的叶子结点分配完，从而完善T₀。

(6) 重复上述5个步骤直到生成了要求数量的后代个体，并且这些后代个体是各不相同的。

该杂交算子从结构上不同于二进制编码、实数编码以及其他结构式编码的杂交操作仅仅简单交换部分基因，而是将2个个体合并后重新进行分配。这样既可以保证其后代结合了2个父代染色体的共同基因，又可保证后代个体是一棵合法的树；既符合了实际应用中物理磁盘阵列和逻辑磁盘之间的映射关系，又增加了群体内的多样性。

4.6  变异操作

变异操作的目的在于保持种群的多样性，避免求解过程陷入局部最优。变异算子用一个很小的概率(即变异率)P_m随机地改变染色体串上的1位或多位基因。其效果是增加了种群的多样性，扩大了搜索空间。本文设计的变异算子描述如下：

(1) 根据变异率P_m随机地选择要进行变异的个体。

(2) 在选中的每个个体中随机选择2个第2层结点(即根结点的2个儿子结点)。

(3) 产生一个随机数δ(1≤δ≤q，q=M/N)，将2个儿子结点下面的从左至右的第δ至第q个叶子结点进行对换。

由于结点之间的交换是在一个解的内部进行的，所以变异后产生的结果仍然是一个合法的解。

4.7  空间信息素更新

随着种群一代代进化，子空间的信息量也不断积累。为了避免残留信息素过多从而淹没其他启发信息，因此，在每一个循环结束后必须对残留的信息量进行更新处理。处理方法如下：

      (15)

其中：Ph_k(t)表示个体S_k所对应的子空间k在第t代的信息量，Ph_k(t-1)表示子空间k在第t-1代的信息量，ρ表示信息素挥发系数，其取值范围为：ρ∈[0，1)，Ph′_k(t)表示第t代操作后子空间k上新加入的信息量。

假设在子空间k上，第t代以前具有最大适应度值的个体为S_{k max}，第t代选择、杂交和变异操作后，子空间k上的个体为S_k(t)。如果f (S_k (t))＞f (S_{k max})，则S_{k max}=S_k(t)，否则，S_{k max}不变。由此，得出：

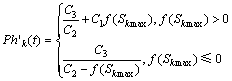     (16)

其中：C₁，C₂和C₃为根据具体问题而设定的正常数，且C₂＞C₃。

4.8  算法的终止条件

由于本文的目标是寻找一种解，使得磁盘阵列组的热度变化满足预定的热度约束条件，从而实现磁盘阵列的负载均衡。因此当满足以下条件之一时，本算法自动终止。

(1) 在种群中至少存在一个满足热度约束条件的个体，在这些个体中选出适应度最大的个体。

(2) 操作循环数达到所允许的最大值。

5  实验分析

为验证本文所提出的I-GA算法的正确性和有效性，进行了一系列仿真实验。实验中，根据相关理论要求和实际应用特点，对本算法的部分参数进行如下设定：

(1) 假设在某一具体应用中，A=2.5，C₁=1，C₂=2，C₃=1。

(2) 信息素启发式因子α和期望启发式因子β分别反映蚂蚁在运动过程中所积累的信息量和适应度在指导蚁群搜索中的相对重要程度。只有正确选定它们的搭配关系，才能避免在搜索过程中出现过早停滞或陷入局部最优等情况的发生^[14]。根据反复实验，我们设定：α=1，β=4。

(3) 由于信息素挥发因子ρ直接关系到算法的全局搜索能力及其收敛速度，根据文献[14]可知，当1-ρ≈0.5(即ρ≈0.5)时，蚁群算法的全局收敛性和收敛速度都比较好，计算性能也比较稳定。所以在本算法中设定：ρ=0.5。

(4) 根据定理：具有变异概率P_m∈(0，1)，交叉概率P_c∈[0，1]，同时采用比例选择法且在选择前保留当前最优解的遗传算法可收敛到全局最优解^[15]。为使算法具有良好的收敛性，将本算法的控制参数进行如下设定：种群规模P_size=50，复制概率P_r=0.1，杂交概率P_c=0.9，变异概率P_m=0.02。

该实验主要测试算法的以下3个方面的性能，并通过与遗传算法的比较进行有效地分析和验证。

5.1  算法的运行效率

在实验中，共进行了4组测试，分别为：

(1) 物理磁盘阵列数为3，逻辑磁盘数为12(N=3，M=12)。

(2) 物理磁盘阵列数为5，逻辑磁盘数为20(N=5，M=20)。

(3) 物理磁盘阵列数为7，逻辑磁盘数为28(N=7，M=28)。

(4) 物理磁盘阵列数为10，逻辑磁盘数为40(N=10，M=40)。

为使本算法具有较快的收敛速度，将其热度变化值约束设定为σ₀ = 0.38。并在同样的参数和约束条件下，采用单纯的遗传算法(GA)也进行了同样的4组测试。采用2种不同算法得到结果分别所需要的遗传数如图3所示。

图3  I-GA和GA所需遗传数

Fig. 3  Required genetic times of I-GA and GA

从图3可知：在分别使用本文提出的I-GA算法和单一采用GA算法的4组测试中，除第1组测试(N=3)获得有效解所花费的遗传代数相同外，其他3组测试，I-GA算法所花费的遗传代数明显比GA算法的少。由此可知，I-GA算法运行效率比GA算法的高。

由于本算法的目标是在满足热度约束条件的若干个个体中选出适应度最大的个体，但并不会由于一味追求效率而使得获得的有效解的适应度较差。图4分别列出了使用这2种算法在进行了上述4组测试后所获得的有效解的适应度。由此可知I-GA算法不仅保持了较高的运行效率，其获得的解也是较GA算法的优。

图4  根据I-GA和GA获取有效解的适应度

Fig. 4  Fitness values of effective solution corresponding to I-GA and GA

5.2  算法的收敛性分析

在本算法中，影响算法收敛性的一个主要因素是选择策略。为了既保证较快的收敛速度，又避免过早收敛，本文在复制操作和杂交操作中设计了不同的选择概率。在复制操作中，选择概率是由个体适应度和所对应子空间信息量的函数来决定的；而杂交操作中只采用了相对适应度作为选择概率。这样能使最优个体具有较高的复制数目，加快算法的收敛速度，又能在一定程度上降低选择压力，保持群体的多样性，避免算法过早收敛。此外，为避免算法过早收敛，本算法在杂交操作中还引入了检测并去除群体中重复个体的思想。

在本算法中，影响算法的收敛性的因素还有，热度变化约束条件σ₀。σ₀越小，获得的解的适应度就越大，就越接近最优解，但是其收敛时间就越长。特别是，如果σ₀=0，则得到的结果就是最优解，体现在物理磁盘阵列上就是各磁盘阵列上的数据分配是绝对的平均，即完美的负载均衡。但这通常很难实现，是要以较长的运行时间为代价的。而反过来，σ₀越大，获得的解的适应就越小，但是相对越容易收敛。为使本算法既具有较好的收敛性，同时又能够获得较优的解，定义σ₀的取值范围为σ₀ ∈[0, 0.5]。

下面进行这样一组实验：物理磁盘阵列为5个；逻辑磁盘为20个，各逻辑磁盘在时间段T的热度分别如表1所示。通过一系列测试发现，当σ₀取值为0.1时，可以得到比较优的解，虽然运行所花费的遗传代数较多，然而与GA相比较还是具有较强的优势，如表2所示。

表1  各逻辑磁盘及相应的热度

Table 1  Heat values of logic disks

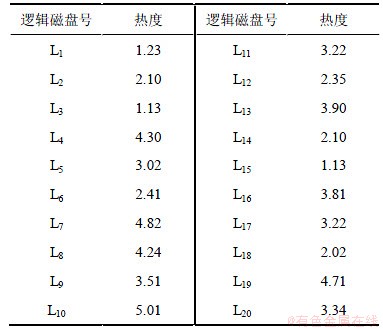
表2  I-GA和GA实验参数和结果比较

Table 2  Experiment parameters and result of I-GA and GA

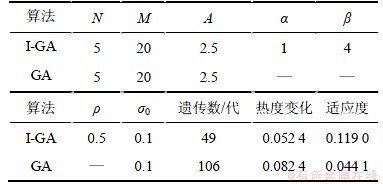
5.3  算法效果分析

为验证本算法的有效性，以N=5，M=20，σ₀=0.1这组实验为例对算法效果进行分析。在使用该算法前，物理磁盘阵列和逻辑磁盘的映射关系如图5所示。通过使用I-GA算法，最终获得了一个新的映射方案，如图6所示。

通过该算法可以获得在新的映射方案下，各物理磁盘阵列的热度(负载)如图7所示。在图7中还将其与未使用本算法前各物理磁盘阵列的热度进行了比较。通过实验结果比较发现，使用本文所提出的I-GA算法，物理磁盘阵列上的数据能够得到有效的分配和优化，而且使各物理磁盘阵列的负载比较平均。由此可以表明该算法能够有效解决磁盘阵列负载不均的问题。

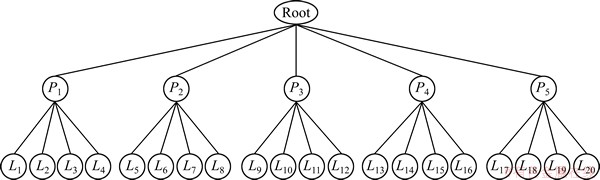
图5  使用I-GA算法前的磁盘映射关系

Fig. 5  Mapping relationship before using I-GA

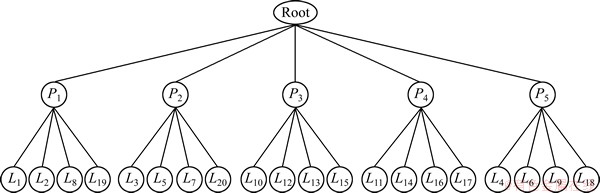
图6  使用I-GA算法后获得的映射方案

Fig. 6  Mapping relationship after using I-GA

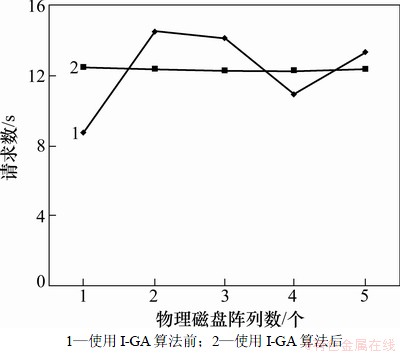
图7  实验结果

Fig. 7  Effect of algorithm

6  结论

(1) 构建了一个由多个磁盘阵列组成的存储子系统，并在此基础上建立了基于分条技术的磁盘阵列数据模型。该模型能够很好地显示逻辑磁盘与物理磁盘阵列之间的映射关系。物理磁盘阵列的热度(也称为负载)是由映射到它上面的逻辑磁盘的热度相加得到，而对逻辑磁盘的热度主要采用一种动态测量的方法。这与实际应用中磁盘阵列的负载会随时间变化而变化是相符合的，同时也弥补了其他文献只考虑静态数据分配的不足。

(2) 针对存储子系统中磁盘阵列之间的负载不均问题首先设计了一个判断标准，并由此提出了一种基于改进型遗传算法来实现动态负载均衡的方法。该方法将蚁群算法与遗传算法结合起来，更快更好地实现磁盘阵列之间的负载均衡。在设计I-GA算法的过程中，结合本文的特点对各项操作也做了相关的改进和完善，并对其进行了一系列仿真实验，测试结果证明本文提出的改进型遗传算法具有更高的运行效率和更好的收敛性。

参考文献：

[1] XIE Tao. SEA: A striping-based energy-aware strategy for data placement in RAID-structured storage systems[J]. IEEE Transactions on Computers, 2008, 57(6): 748-761.

[2] Kim M Y. Synchronized disk interleaving[J]. IEEE Transaction on Computers, 1986, 35(11): 978-988.

[3] Ganger G R, Worthington B L, Hou R Y, et al. Disk subsystem load balancing: Disk striping vs. conventional data placement[C]//Proceedings of the 26th Hawaii International Conference on System Sciences, Los Alamitos: IEEE CS Press, 1993: 40-49.

[4] Ganger G R, Worthington B L, Hou R Y, et al. Disk arrays: High-Performance, high-Reliability storage subsystems[J]. IEEE Computer, 1994, 27(3): 30-36.

[5] Scheuermann P, Weikum G, Zabback P. Data partitioning and load balancing in parallel disk systems[J]. The VLDB Journal, 1998, 7(1): 48-66.

[6] Scheuermann P, Weikum G, Zabback P. Adaptive load balancing in disk arrays[C]//David B L. Proceedings of the 4th International Conference on Foundations of Data Organization and Algorithms. Verlag London: Springer, 1993: 345-360.

[7] 董欢庆, 李战怀. 基于遗传算法的RAID磁盘阵列中磁盘负载均衡方法[J]. 计算机工程与应用, 2003, 39(16): 41-42.

DONG Huanqing, LI Zhanhuai. Disk load balancing method for RAID disk array based on the genetic algorithm[J]. Computer Engineering and Application, 2003, 39(16): 41-42.

[8] 杜永贵, 石洪献. 混合遗传算法的研究现状[J]. 科技情报开发与经济, 2006, 16(10): 1084.

DU Yonggui, SHI Hongxian. Research on the current situation of hybrid genetic algorithm[J]. SCI-TECH Information Development & Economy, 2006, 16(10): 1084.

[9] Carballeira G F, Calderon A, Carretero J, et al. The design of the expand parallel file system[J]. International Journal of High Performance Computing Applications, 2003, 17(1): 21-37.

[10] Gradecki J D, Ra I. An adaptive-learning distributed file system[C]//Negoita M G. Knowledge-Based Intelligent Information and Engineering Systems 2: 8th International Conference. Wellington: Springer, 2004: 637-646.

[11] NI Yunzhu, LI Zhishu. Minimizing the response time of a striped disk array[C]//Proceedings of the 2010 International Conference on Intelligent Human-Machine Systems and Cybernetics. Nanjing: IEEE Computer Society, 2010: 200-204.

[12] 倪云竹, 吕光宏, 黄彦辉. 用遗传算法解决基于分条技术的磁盘负载均衡问题[J]. 计算机学报, 2006, 29(11): 1995-2001.

NI Yunzhu, L Guanghong, HUANG Yanhui. The solution of disk load balancing based on disk striping with genetic algorithm[J]. Chinese Journal of Computers, 2006, 29(11): 1995-2001.

[13] 倪云竹. 用遗传算法解决基于分条技术的磁盘负载均衡问题[D].成都: 四川大学计算机学院, 2004: 19-20.

NI Yunzhu. The solution of disk load balancing based on disk striping with genetic algorithm[D]. Chengdu: Sichuan University. College of Computer, 2004: 19-20.

[14] 段海滨. 蚁群算法原理及其应用[M]. 北京: 科学出版社, 2005: 100-116.

DUAN Haibin. Ant colony algorithms: Theory and applications[M]. Beijing: Science Press, 2005: 100-116.

[15] 潘正君, 康立山. 演化计算[M]. 北京: 清华大学出版社, 1998: 10-42.

PAN Zhengjun, KANG Lishan. Evolutionary computation[M]. Beijing: Tsinghua University Press, 1998: 10-42.

(编辑  陈爱华)

收稿日期：2012-09-22；修回日期：2012-12-13

基金项目：浙江省科技计划项目(2008C21081)

通信作者：倪云竹(1978-)，女，四川甘洛人，博士，讲师，从事计算机网络与信息系统、存储技术研究；电话：13666244216；E-mail：niyunzhu@scu.edu.cn