Model on medium range order in liquid Al-Fe alloys

QIN Jing-yu(秦敬玉), QIN Xu-bo(秦绪波), WANG Wei-min(王伟民), BIAN Xiu-fang(边秀房)

(Key Laboratory of Liquid Structure and Heredity of Materials, Ministry of Education, Shandong University, Ji′nan 250061, China)

Abstract: Numerical analysis confirms that in some cases the prepeak in the structure factor causes obvious change in the coordination number, but change in the interatomic distance can be neglected for the study of the medium range order(MRO). In order to model the MRO, it is not possible to get enough information based on the pair correlation function; however the quasi-Bragg equation can be employed to characterize the quasi-period of MRO corresponding to the prepeak position. By assuming that the interatomic distance between Fe and Al atoms hardly varies with composition, structural models were constructed based on the B2-type structure units of ordered FeAl alloy. The quasi-periods for different alloys obtained from the model structures are in reasonable agreement with the experimental ones.

Key words: Al-Fe alloy; molten structure; medium range order CLC number: TG146; TG111

Document code: A

1 INTRODUCTION

In 1966 Steeb et al^[1] found that in the structure factor of liquid Mg-Sn alloy by X-ray diffraction there existed a prepeak. The prepeak is the peak in the structure factor preceeding the main(strongest) peak. Sometimes the prepeak in the structure of molten alloys was neglected^[2]. Homtova et al^[3] suggested that prepeak was indicative of fragments of crystalline Fe₂Al₅ compound in the liquid Al-Fe alloys. Price et al^[4] motivated the concept of medium range order(MRO) in liquid and amorphous materials as the nature of the prepeak. So far, a majority of investigations on MRO are devoted to amorphous materials^[5], molecular liquids^[4], IA-IVA alloy melts^[6] and glassy super- ionic conductors^[7].

It is well known that there are many important traditional industrial materials in Fe-Al alloy system. Many kinds of new materials have been developed in this system. The amorphous Al-Fe-Re alloys^[8] and quasi-crystalline phase in rapidly solidified Al-Fe alloys have been reported^[9]. Some Fe-Al alloys exhibit interesting magnetic properties^[10], and Fe₃Al-based intermetallic compounds may be applied as high temperature materials^[11] and the important component for ceramic composites^[12]. X-ray diffraction analysis shows that there is medium range order in liquid Fe-Al alloys^[13], and a further study on this subject may shed light on the structural relationship between the liquid state and the solid phase, which will facilitate the design and manufacture of the Fe-Al based materials.

Generally there are not chemically stable units in metal-metal alloys, which makes it even more difficult to analyze the MRO in such alloys. In this work, the interatomic distance between Fe and Al atoms was hypothesized to be constant; the evolution of the MRO in Fe-Al alloy melts were modeled by using the structure units of B2-type FeAl alloy.

This paper is arranged as follows. Firstly the manifestation of the prepeak in real space is studied, and then the experimental data are given followed by modeling of the MRO structure. A conclusion is drawn finally.

2 MANIFESTATION OF PREPEAK IN REAL SPACE

2.1 Relationship between S(Q) and g(r)

Structure factor S(Q) and pair correlation function g(r) are two important functions in amorphous structure analysis which are related with each other by Fourier transformation as expressed in the form of equation(1):

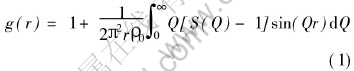
where ρ₀ is the number density of amorphous materials. In practice the upper limit of the integral is a limited value that is 125.0nm^-1 with respect to the MoKα radiation. The structure factor of liquid Ga is employed with different artificial prepeaks to study the manifestation of the prepeak in real space.

2.2 Numerical test on artificial prepeaks

The artificial prepeaks were sorted out into two classes. The first class(No.Ⅰ) included prepeaks with the same position(Q_p) and different height(HPP), while those with different Q_p but the same HPP and half width were ranked as the second class(No.Ⅱ). These two classes of modified S(Q) are shown in Fig.1 and Fig.2 respectively together with the S(Q) with no prepeak for comparison. The structure factors in the regime beyond 20nm^-1 resemble each other so closely that the difference between them is hard to perceive.

Fig.1  Structure factors with same position but different height of prepeak(HPP)

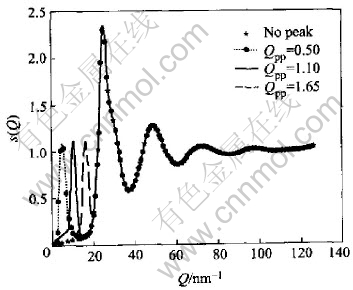
Fig.2  Structure factors with same height(HPP) but different position of prepeak

   Fig.3 and Fig.4 include pair correlation functions corresponding to Fig.1 and Fig.2 respectively. In the case of the first class, the difference among the first peak of g(r) can be neglected, while there is a little change in their heights of g(r) in the second class. For both classes the difference mainly emerges within the range of 0.35-0.55nm where the curves resemble each other in shape and no new hump or vale is observed. The only difference among the curves is observed in terms of the height.

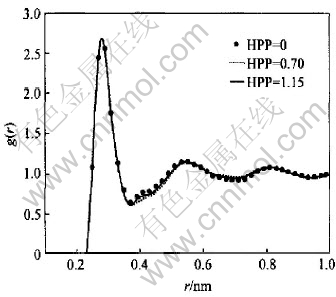
Fig.3  Pair correlation functions inferred from structure factors with same position but different HPP

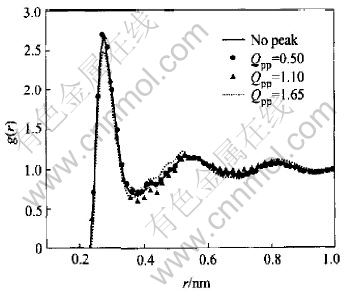
Fig.4  Pair correlation functions inferred from structure factors with same HPP but different position of prepeak

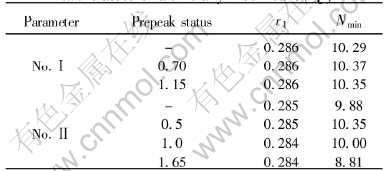
   The nearest neighbor distance r₁ and coordination number N_min which are the first peak position of g(r) and the area under first maximum of radial distribution function 4πr²ρg(r) respectively are calculated and listed in Table 1.

As shown in Table 1, the difference in terms of r₁ among seven kinds of prepeak status can be neglected, but the largest deviation up to -10.8% with respect to N_min is observed in the second class. This kind of behavior makes it not reliable to model the MRO based on g(r) from X-ray diffraction experiment.

Table 1 Real space parameters for two classes of artificially modified S(Q)

2.3 Analysis on experimental error

The small fluctuation superposing in the second maximum of g(r) in Fig.4 may be resulted from the experimental error in S(Q) near Q_max. For instance, the S(Q) with no prepeak in Fig.2 has the values of 1.028 and 0.998 at 125.0nm^-1 and 110.0nm^-1 respectively. It is thought that S(Q) bears less error at 110.0nm^-1 than at 125.0nm^-1 according to the trend in S(Q) in the regime of large Q. Unlike the case of 125.0nm^-1, the termination of Q at 110.0nm^-1 can suppress the fluctuation effectively as shown in Fig.5.

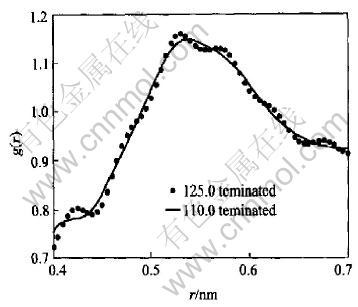
Fig.5  Effect of termination at different Q_max on second maximum of g(r)

   There is always a hump around 0.42nm in every g(r) that could be attributed to the contribution of both the experimental and the termination error through equation(1). Fig.6 lays out the behavior of the estimated error on g(r). More detailed analysis on the experimental error transferred from S(Q) to g(r) can be found in Ref.[14].

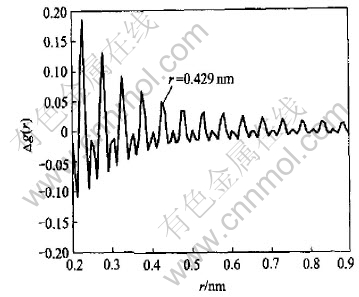
Fig.6  Estimated variation of g(r) on account of experimental and termination error

   As pointed out by Salmon^[15], the loss of structural information during Fourier transformation from S(Q) to g(r) through equation(1) results from the small weight of S(Q) in the regime of small Q. From the physical point of view, g(r) is the statistical information between any two atoms, and no consideration is paid to the impact from a third atom. Since the three dimension structure information is kneaded into a one dimensional function. Naturally with r increasing beyond the first maximum of g(r), more and more atoms fall into the shell between r to r+dr, thus information on MRO is smoothed away by the short-range order information. Even in a crystal as r increases, the pair spacings pack closer and closer together, until they disappear into a smooth background. It is the four-body atom distribution function that is sensitive to MRO in fluctuation electron microscopy measurement^[16]. Now that g(r) is not sufficient to demonstrate MRO, the quasi-Bragg equation should be used to reveal insight into MRO.

3 EXPERIMENTAL DATA AND MRO STRUCTURE MODELING

Plotted curves in Fig.7 are the structure factors from the experiment whose description was

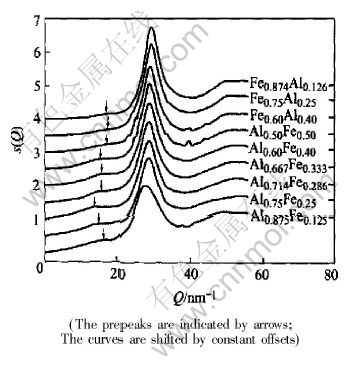
Fig.7  Structure factors inferred from X-ray diffraction experiment on Fe-Al melts

given in Ref.[13]. The Q_p was measured after a prepeak separation procedure, and then the quasi-Braggequation in the form of equation(2) was employed to evaluate the quasi-period of MRO that is then plotted in Fig.8 and compiled in Table 2.

d_p=2πQ^-1_p(2)

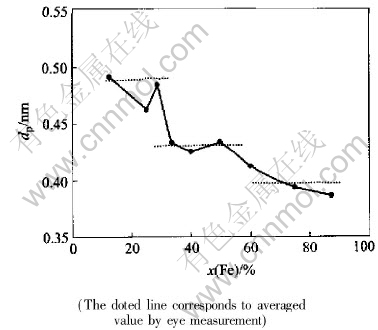
Fig.8  Quasi-period of MRO evaluated from quasi-Bragg equation with respect to Fe content^[13]

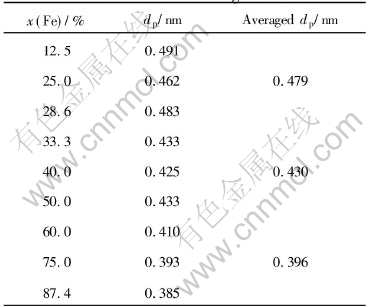
Table 2 Quasi-periods for different alloy melts and their averaged values

   Ahead of constructing MRO models in Fe-Al alloy melts, experimental results on four intermetallic alloys from other researchers^[17-20] are collected into Table 3 which includes the nearest Al neighbors of a Fe atom named N_FeAl, the nearest Fe neighbors of a Al atom named N_AlFe, the averaged nearest neighbor distance between Fe and Al atoms named d_FeAl, the averaged nearest neighbor distance between Al atoms named d_AlAl. The clustering information from diffusion experiment of Fe in Al melt^[21] and the experimental value of d_AlAl in pure Al melt^[22] are also put forward.

As provided in Table 3, the values of d_FeAl for the four intermetallic alloys are a little more than

Table 3 Partial coordination numbers and interatomic distances quoted from other studies

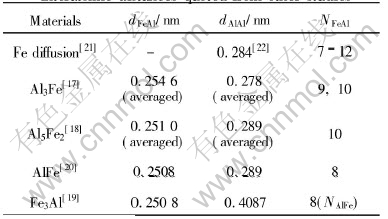
0.25nm. Moreover in the Al-rich alloys each Fe atom is surrounded by 9 or 10 Al atoms^{[17, 18]}, while in the Fe₃Al(DO₃) each Al atom has 8 Fe nearest neighbors^[19]. In FeAl(B2) alloy Al and Fe atom are confronted with the same environment in which each atom has 8 unlike-atom nearest neighbors^[20]. The anomalous diffusive behavior of Fe atom in Al melt suggested 7-12 Al atoms clustering around one Fe atom^[21]. On account of such information, a hypothesis was made that in Fe-Al alloy melts one kind of cluster took the form of the B2 structure units as in FeAl intermetallic alloy, with the d_FeAl being 0.2508nm and not varing with composition. Then MRO structure modeling was executed by packing the units in some specific ways with the quasi-period of MRO being generally the correlation distance between the like-atoms of the minor type.

It is brought forth by crystal structural data^[18] and ab-initio calculation^[23] that there is strong interaction between Al and Fe atoms. This lays the foundation for the hypothesis of constant d_FeAl in this work.

Firstly the Fe-rich alloys of Fe_0.874Al _0.126, Fe_0.75Al_0.25 and Fe_0.60Al_0.40 were modeled. In Fig.9, the packing of two units in directions of 〈110〉 between which one edge is shared gives a d_AlAl of 0.409nm as the required quasi-period. The unit used in Fig.9 is the same as that of the B2 structure of FeAl intermetallic alloy, and the packing manner resembles the DO₃ configuration of ordered Fe₃Al alloys.

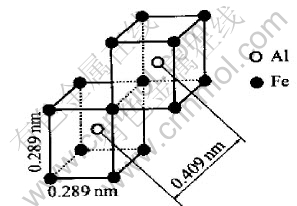
Fig.9  Units packing in directions of 〈110〉,and sharing one edge between units

Then modeling on the Al-rich alloys of Al_0.875Fe_0.125, Al_0.75Fe_0.25 and Al_0.714Fe_0.286 was performed. A new type of unit, which can also be found in the B2-type FeAl alloy, was created in Fig.10 by exchanging seats between the Al atom and the Fe atom of the unit in Fig.9. Then the configuration by packing units in Fig.10 in directions of 〈111〉 and sharing one corner gives d_FeFe a value of 0.500nm as quasi-period.

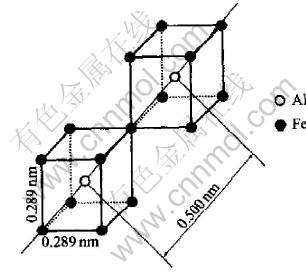
Fig.10  Units packing in directions of 〈111〉, and sharing one edge

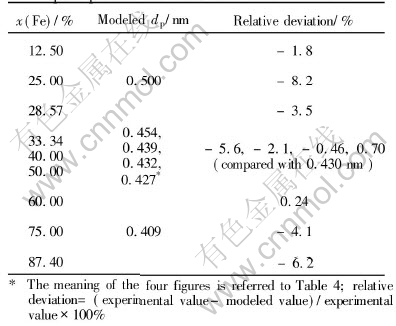
   Modeling on the alloys of Al_0.667Fe_0.333, Al_0.60Fe_0.40 and Al_0.50Fe_0.50 was rather complicated. Except for what are discussed in Fig.9 and Fig.10, another kind of packing manner in which face-sharing like-units arranged along the 〈100〉 direction may exist. In such a way as shown in Fig.11, the configuration will resemble that of B2 structure of FeAl intermetallic alloy in which Fe and Al atom hold the same environment where not only the second neighbor but also the third one would contribute to the prepeak. Since each Fe or Al atom has the second and the third neighbors at 0.409nm and 0.500nm respectively, the quasi-period should be the weighted average of these two distances as shown in Table 4.

So far quasi-periods were determined from the

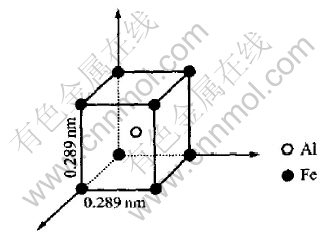
Fig.11  Packing of structure units along normal axes, i.e. directions of 〈100〉

Table 4 Possible values of quasi-period evaluated from weighted averaging between 0.409nm and 0.500nm

 three kinds of configuration, and compared with their experimental counterparts in Table 5. Reasonable agreements between modeling and experiment are achieved except that the relative error is more than 5% in cases of Al_0.75Fe_0.25, Fe_0.874Al_0.126 and of equal weighting referred to Table 4.

Table 5 Comparison between experimental quasi-periods and those from structure models

   It is possible that in Table 4 the second and third neighbor distance may not be on equal terms. Moreover the second one should have larger weight than the third one, which can suppress the relative difference within the range of ±2.1%. Since the atomic ratio of Fe/Al in Fe_0.874Al_0.126 is nearly the inverse of Al/Fe ratio in Al_0.875Fe_0.125, the distribution of minor type atom and then the quasi-periods are expected to be similar. In fact this is not the case as shown in Table 1 for which the reason is not understood. As for alloy Al_0.75Fe_0.25, it is approximant of quasicrystal. The suggestion that there was icosahedral short-range order in the Al₁₃- Fe₄ melt^[24] may partially explain its large deviation from the experimental value.

In real alloy melts, there exist lots of structural defects. The packing manners of units in Figs.9-11 should be modified, and the B2-type structure units that would be substituted by polyhedrons with about 10 unlike-atoms coordination may be too perfect to represent the clusters in the melts. Presently serious difficulty is confronted to reveal the structural details of the clusters in Fe-Al alloy melts by normal X-ray diffraction. Furthermore, the experiment was conducted under the constant temperature instead of the equal overheating scheme. A further structural modeling should take into account the different X-ray scattering ability of the Fe and Al atoms apart from their geo- metric and topological properties.

4 CONCLUSIONS

It is shown by numerical analysis that the change in position or height of the prepeak will sometimes only affects the coordination number, so it is impossible to understand the medium-range order in the non-crystalline materials through g(r); on the contrary the quasi-Bragg equation associated with S(Q) can be used in this respect.

On the hypothesis that d_FeAl is a constant in different molten Fe-Al alloys, the quasi-periods of MRO in such melts are satisfactorily modeled by different packing of B2 structure units. The structural models thus constructed resemble the configuration of B2 or DO₃ type ordered alloy to some extent.

REFERENCES

[1]Steeb S, Entress H. Atomverteilung sowie spezifischer elektrischer widerstand geschmolzener magnesium-zinn-legietungen [J]. Z Metallkde, 1966, 57: 803-807.(in German)

[2]Kita Y, van Zytveld J B, Morita Z, et al. Covalency in liquid Si and liquid transition-metal- Si alloys: X-ray diffraction studies [J]. J Phys: Condens Matter, 1994, 6: 811-820.

[3]Homutova Z V, Slukhovskii O I, Romanova A V. Stroenie rasplavov aluminii-felezo [J]. Ukr J Phys,1986, 31(7): 1045-1051.(in Russian)

[4]Price D L, Moss S C, Reijers R, et al. Intermediate-range order in glasses and liquids [J]. J Phys: Condens Matter, 1989, 1(5):1005-1008.

[5]Elliott S R. Medium-range structural order in covalent amorphous solids [J]. Nature, 1991, 354: 445-452.

[6]Alblas B P, van der Lugt W, Dijkstra J, et al. Structure of liquid Na-Sn alloys [J]. J Phys F: Metal Phys, 1983, 13(12): 2465-2477.

[7]Elliott S R. Isotopic-substitution neutron diffraction as a probe of the structural environment of cations in superionic glasses [J]. Solid State Ionics, 1998, 105(1/4): 39-45.

[8]Hsieh H Y, Egami T, He Y, et al. Short range ordering in amorphous Al₉₀FexCe_10-x [J]. J Non-Cryst Solids, 1991, 135(2/3): 248-254.

[9]Zou X D, Fung K K, Kuo K H, Orientational relationship of decagonal quasicrystal and tenfold twins in rapidly cooled Al-Fe alloy [J]. Phys Rev B, 1987, 35: 4526-4528.

[10]Wu D, Baker I. Strain-induced ferromagnetism in FeAl single crystals [J]. Mat Sci and Eng A, 2002, 329/331: 333-337.

[11]Stoloff N S, Liu C T, Deevi S C. Emerging applications of intermetallics [J]. Intermetallics, 2000, 8(9-11): 1313-1320.

[12]Crimp M J. A novel approach to intermetallic matrix composite(IMC) processing [J]. Mater Sci Eng A, 1995, 192-193: 633-639.

[13]Qin J Y, Bian X F, Sliousalianko S I, et al. Pre-peak in the structure factor of liquid Al-Fe alloy [J]. J Phys: Condens Matter, 1998, 10: 1211-1218.

[14]Egami T. Structure studies by X-ray and neutron diffraction: how accurate are they? [J]. Mater Sci Eng A, 1994, 179/180: 17-19.

[15]Salmon P S. Real space manifestation of the first sharp diffraction peak in the structure factor of liquid and glassy materials [J]. Proc R Soc Lond A, 1994, 445: 351-365.

[16]Voyles P M. Fluctuation electron microscopy of medium-range order in amorphous silicon [D]. Urbana-Champaign: University of Illinois, 2001, 1-22.

[17]Black P J. The structure of FeAl₃ I [J]. Acta Cryst, 1955, 8: 43-48.

[18]Black P J. Structural relations between intermetallic compounds [J]. Acta Metall, 1956, 4: 172-179.

[19]Popiel E, Tuszynski M, Zarek W, et al. Investigation of Fe_3-xVxAl alloys with DO₃ type structure by X-ray, magnetostatic and Mossbauer effect methods [J]. J Less-Common Metals, 1989, 146: 127-135.

[20]Taylor A, Jones R M. Constitution and magnetic properties of iron-rich iron-aluminum alloys [J]. J Phys Chem Solids, 1958, 6: 16-37.

[21]Turnbull D. The gram-atomic volumes of alloys of transition metals with Al and Si [J]. Acta Metall Mater, 1990, 38: 243-247.

[22]Qin J Y, Bian X F, Wang W M, et al. Characteristic of temperature induced change on the structure of liquid Al and Sn [J]. Phys Sinica, 1998, 47: 438-444.

[23]Manh D Nguyen, Mayou D, Pasturel A, et al. Electronic structure and hybridisation effects in transition-metal-polyvalent-metal alloys [J]. J Phys F: Metal Phys, 1985, 15: 1911-1927.

[24]Holland-Moritz D, Schenk T , Simonet V, et al. Short-range order in undercooled melts forming quasicrystals and approximants [J]. J Alloys Compounds, 2002, 342: 77-81.

(Edited by PENG Chao-qun)

Foundation item: Project(50301008) supported by the National Natural Science Foundation of China

Received date: 2004-03-17; Accepted date: 2004-08-21

Correspondence: QIN Jing-yu, PhD; Tel: +86-531-8392810; E-mail: qinjy@sdu.edu.cn